
Математическое моделирование в механике композиционных материалов и
..pdf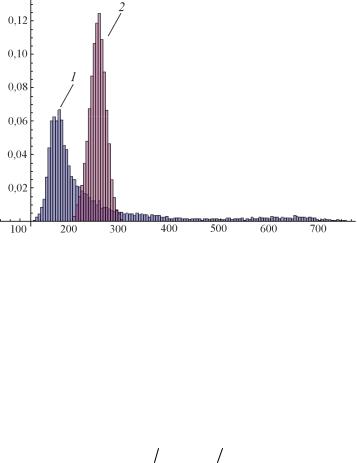
Рис. 7. Распределение вероятной для двух способов размещения точек по треугольникам: 1 – гистограмма с длинным «хвостом» соответствует рис. 6, а; 2 – локализованная гистограмма соответствует рис. 6, б
Для определения зависимости равновесного межатомного расстояния выбранной кристаллической решетки от амплитуды возмущений рассматривается монокристалл в форме, симметрия которой соответствует симметрии решетки. Для каждого заданного значения амплитуды A при произвольных параметрах решетки (два параметра a иb для графита, один параметр a для графена) и произвольных параметрах
α и β |
|
12 |
6 |
Леннарда-Джонса вы- |
|
потенциала ϕ(r) =β (α r) |
−2(α r) |
|
|||
|
|
|
|
|
|
числяется полная потенциальная энергия атомов образца. Будем использовать вариационноеуравнение статики сплошнойсреды ввиде
δU = δA +δQ , δA = ∫tn δuds +∫ρf δu dv ,
S1 |
V |
|
где δU – вариация внутренней энергии образца, |
δA – вариация ра- |
|
боты внешних поверхностных tn и объемных ρf |
сил, δQ – приток |
|
тепла, δu – кинематически допустимые вариации перемещений.
31
В качестве варьируемых параметров выбираются неизвестные параметры решетки a и b. Приток тепла определяется интегралом
δQ = ∫ρT δS dv ,
V
где T – температура, S – энтропия системы. Поскольку задаваемое при исследуемом переходе от одного равновесного состояния к другому приращение амплитуды колебаний атомов строго фиксировано, то варьирование параметров решетки a и b происходит при постоянном значении температуры T. Энтропия кристалла S не зависит от значений a и b, следовательно, δS = 0 и подводимое к образцу тепло также не зависит от варьируемых параметров решетки: δQ = 0. Объемные силы в рассматриваемом случае на образец не
действуют. Поверхностные силы в зависимости от постановки задачи могут быть заданы любыми, например соответствовать гидростатическому давлению при исследовании его влияния на кристалл.
Вданном случае они принимаются равными нулю, поэтому δA = 0. Таким образом, для определения равновесных параметров кристаллической решетки при заданной температуре (амплитуде и частоте тепловых колебаний атомов) необходимо удовлетворить условие δU = 0. В силу выпуклости потенциальной энергии кристаллического образца требуется найти ее минимум по двум переменным a и b.
Вработе для решения задачи минимизации можно использовать метод Хука – Дживса или метод Нелдера – Мида, программу для реализации которых предлагается написать самостоятельно или воспользоваться встроенной функцией FindMinimum пакета Mathematica для поиска минимума заданной функции.
6.2.4. Математическая модель уплотнительного кольца из наноструктурированного терморасширенного графита
Традиционные способы отработки (комплексные испытания, внесение изменений в существующие конструкции и технологии изготовления) уплотнительных элементов из наноструктурированного
32
ТРГ (УЭ) неоправданны вследствие высокого риска возникновения аварий на особо опасных промышленных предприятиях и производствах, которые могут сопровождаться серьезным экологическим и экономическим ущербом. Поэтому большое значение приобретают методы математического моделирования поведения ТРГ, с помощью которых можно прогнозировать теплофизические и механические свойства ТРГ, проектировать новые уплотнительные элементы (УЭ), оптимально соответствующие условиям нагружения конкретной конструкции, узла или агрегата.
УЭ является толстостенным, ограниченным по высоте однородным трансверсально-изотропным цилиндром (поперечное сечение ограничено двумя концентрическими окружностями радиусами a и b , a <b ), ось симметрии бесконечного порядка z ( 0 ≤ z ≤ h , h – высота) которого совпадает с образующей. Выберем цилиндрическую ортогональную систему координат r , θ и z таким образом, чтобы ось z совпадала с осью симметрии УЭ.
В процессе термосилового нагружения компоненты тензора напряжений σij удовлетворяют в отсутствие массовых сил уравнени-
ям равновесия |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂σrr + |
|
1 |
∂σrθ + |
|
∂σzr |
|
+ σrr −σθθ = 0; |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||
∂r |
|
r |
|
∂θ |
|
|
∂z |
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|||||||
|
∂σrθ |
+ |
|
1 |
∂σθθ + ∂σzθ |
+ |
2σrθ |
= 0; |
|
|
|
(6) |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
∂r |
|
|
|
|
r |
∂θ |
|
|
|
|
∂z |
|
|
r |
|
|
|
|
|
|
|
|
|||||
|
∂σzr + |
1 |
∂σθz |
+ ∂σzz |
+ |
|
σzr |
= 0, |
|
|
|
|
|||||||||||||||||
|
r |
|
r |
|
|
|
|
||||||||||||||||||||||
|
|
∂r |
|
|
|
|
|
∂θ |
|
|
|
|
∂z |
|
|
|
|
|
|
|
|
|
|
||||||
а бесконечно малые деформаций εij |
|
связаны с компонентами векто- |
|||||||||||||||||||||||||||
ра перемещений ui |
геометрическими соотношениями Коши: |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
∂u |
r , εθθ = |
1 |
∂u |
|
|
|
|
|
|
|
|
||||||||||||
|
|
εrr |
= |
|
|
|
|
|
|
|
|
|
|
r +ur |
, |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
∂r |
|
|
|
|
|
r |
∂θ |
|
|
|
|
|
|
|
||||||||
εzz |
= |
∂u |
z , εrθ = |
1 |
1 |
∂u |
r −uθ |
|
+ |
∂u |
θ |
|
, |
(7) |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
2 |
|
|
|
|
|
∂r |
||||||||||||||||||||||
|
|
∂z |
|
|
|
|
|
r |
|
|
∂θ |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
33 |
εθz = |
1 |
|
∂u |
θ + |
1 |
∂u |
z |
|
|
εzr = |
1 |
∂u |
z + |
∂u |
r |
|
|
|
|
|
|
|
|
, |
|
|
|
|
. |
||||||
2 |
|
|
|
2 |
|
|
|||||||||||
|
|
∂z |
r ∂θ |
|
|
|
|
∂r |
∂z |
|
|||||||
Определяющие соотношения, описывающие термоупругое деформирование однородного трансверсально-изотропного материала могут быть представлены следующим образом:
σrr = K11εrr + K12εθθ + K13εzz −βrrT ; |
(8) |
σθθ = K12εrr + K11εθθ + K13εzz −βθθT ;
σzz = K13 (εrr +εθθ)+ K33εzz −βzzT ;
|
|
|
|
|
|
|
|
|
|
|
ˆ |
|
|
|
|
|
|
ˆ |
|
|
|
|
|
σrθ = Gεrθ , σzr = Gεzr , |
σθz = Gεθz . |
|
|
|
|||||||||||||||
Эти соотношения содержат технические постоянные: |
|
||||||||||||||||||||
K |
11 |
= K |
22 |
= |
|
E |
1−νˆ |
2 |
) |
, K |
12 |
= |
E |
( |
ν−νˆ 2 |
) |
, |
|
|||
|
D |
|
D |
|
|||||||||||||||||
|
|
|
|
|
( |
|
|
|
|
|
|
|
|||||||||
|
Eνˆ |
|
|
|
|
|
|
ˆ |
|
|
|
|
|
|
|
|
|
|
|
|
|
K13 = K23 = |
(1+ν), |
K33 = |
E |
(1 |
−ν2 ), D = (1+ν)(1−ν−2νˆ 2 ), |
|
|||||||||||||||
D |
D |
|
|||||||||||||||||||
βrr =βθθ = α (K11 + K12 )+αˆ K13 , |
βzz = 2αK13 +αˆ K33 . |
(9) |
|||||||||||||||||||
ˆ |
|
Здесь E и E , α и αˆ – модули Юнга и коэффициенты линейного |
|
термического расширения в плоскости изотропии |
rθ и в направле- |
|
ˆ |
нии образующей z уплотнительного кольца соответственно, G и G – |
|
поперечный и продольный модули сдвига, ν и νˆ |
– коэффициенты |
Пуассона. |
|
Будем исследовать состояние кольца при стационарном поле температур T . Внутренние источники (стоков) тепла отсутствуют. Тогда распределение T в точках уплотнительных колец будет описываться уравнением вида
λ |
∂ |
∂T |
|
1 |
∂2T |
ˆ |
∂2T |
|
|
||
|
|
r |
|
+ |
r |
∂θ2 |
|
+λ |
∂z 2 |
= 0 . |
(10) |
r |
∂r |
∂r |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
34
Здесь λ и λˆ – коэффициенты теплопроводности в плоскости изотропии rθ и направлении образующей z кольца соответственно. В установившемся равновесном состоянии распределение температуры в штоке и сальниковой камере также является стационарным и потоки тепла через боковые поверхности УЭ отсутствуют:
∂T |
|
∂T |
|
|
|
|
= 0 , |
(11) |
|||
|
|
|
|
||||||||
∂r |
Γ |
= ∂r |
|
|
Γ |
2 |
|||||
|
|
|
1 |
|
|
|
|
|
|
|
|
а на торцевых поверхностях известны значения температуры: |
|
||||||||||
T |
|
Γ3 |
=T1 , T |
|
Γ4 |
=T2 , |
(12) |
||||
|
|
||||||||||
|
|
|
|||||||||
где значения температуры T1 и T2 выражаются через температуры высокоагрессивных и реакционно-способных газов или жидкостей Tint и окружающей среды Text . Обратим внимание на то, что в силу
симметрии тела и граничных условий поле температур не зависит от окружной координаты θ и уравнение теплопроводности примет вид
λ ∂ |
∂T |
ˆ |
∂2T |
|
|
||
|
|
r |
|
+λ |
∂z 2 |
= 0 . |
(13) |
r ∂r |
∂r |
|
|
|
|||
В силу условий (11) в стационарном состоянии поле температуры в уплотнительном кольце не будет зависеть и от радиуса r, следовательно, уравнение (13) примет вид
λˆ ∂2T = 0 ,
∂z 2
решением которого является линейное распределение температуры по высотекольца, независящее откоэффициентов теплопроводности:
T = C1 z +C2 .
Отсчитывая координату z от нижнего торца, получим
T = (T2 −T1)z/H ,
где H – высота кольца.
35
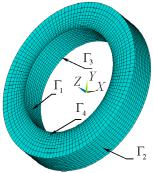
|
Для решения задачи термо- |
|||
|
упругости систему колец из на- |
|||
|
ноструктурированного ТРГ, по- |
|||
|
казанную на рис. 1, заменим |
|||
|
единственным уплотнительным |
|||
|
элементом (рис. 8). Проанализи- |
|||
|
ровав |
условия |
эксплуатации, |
|
|
сформулируем |
следующие |
ги- |
|
|
потезы и соответствующие этим |
|||
|
гипотезам условия на участках |
|||
Рис. 8. Дискретизация участков |
поверхности |
уплотнительных |
||
поверхности уплотнительного |
колец: |
|
|
|
элемента |
1. Будем рассматривать со- |
|||
|
стояние |
установившегося |
поля |
|
температуры штока (или внутренней части колец) и поверхности корпуса сальника в процессе эксплуатации. На внутренней Γ1 и на-
ружной Γ2 поверхностях кольца заданы условия (12). На торцевых поверхностях Γ3 и Γ4 заданы нулевые потоки (11).
2. После сборки и герметизации запорной арматуры УЭ в процессе эксплуатации остаются неподвижными относительно корпуса сальника. Вследствие чего внешняя боковая поверхность Γ2
(см. рис. 8) соприкасается с внутренней поверхностью сальниковой камеры так, что исключаются радиальные, осевые и окружные перемещения:
ur |
|
Γ |
|
= uθ |
|
Γ |
|
=uz |
|
Γ |
= 0 . |
(14) |
|
|
|
|
|
||||||||
|
2 |
|
2 |
|
2 |
|
||||||
|
|
|
|
|
|
|
|
|
|
3.Будем предполагать, что давление на торцевую поверхность
Γ3 , контактирующую с нажимной втулкой, однородно (обеспечива-
ется одинаковыми усилиями затяжки в прижимных болтах) и задано в направлении образующей:
σ |
zz |
|
Γ |
|
= −pfront . |
(15) |
|
|
|||||
|
|
3 |
zz |
|
||
|
|
|
|
|
|
36
Нажимная втулка обеспечивает герметизацию уплотнительного соединения и исключает перемещение точек торцевой поверхности в радиальном и окружном направлениях:
ur |
|
Γ |
=uθ |
|
Γ |
= 0 . |
(16) |
|
|
||||||
|
|
|
3 |
|
|
3 |
|
4.На ограниченном двумя концентрическими окружностями
срадиусами a и d ( a < d ) участке Γ4 торцевой поверхности дей-
ствует однородное давление pzzwork , создаваемое рабочими средами:
σ |
zz |
|
Γ |
|
= −pwork . |
(17) |
|
|
|||||
|
|
4 |
zz |
|
||
|
|
|
|
|
|
Кроме того, точки, принадлежащие этому участку, не способны свободно перемещаться в своей плоскости:
ur |
|
Γ |
= uθ |
|
Γ |
= 0 . |
(18) |
|
|
||||||
|
|
|
4 |
|
|
4 |
|
На участке Γ5 торцевой поверхности, контактирующей с грандбуксой или упорным кольцом, ограниченном окружностями с радиусами d и b ( d <b ), исключены перемещения в радиальном ur ,
окружном uθ и осевом uz |
направлениях: |
|
|
|||||||
ur |
|
Γ |
= uθ |
|
Γ |
= uz |
|
Γ |
= 0. |
(19) |
|
|
|
||||||||
|
|
|
5 |
|
|
5 |
|
|
5 |
|
5. Будем исследовать начальный режим работы, когда уплотнительная арматура собрана и герметизирована, УЭ не приработаны, в результате чего между внутренней поверхностью кольца и поверхностью штока имеет место идеальное сопряжение. В этом случае перемещения точек на участке Γ1 уплотнительного элемента совпа-
дают с перемещениями точек штока, который может совершать воз- вратно-поступательное и вращательное движение. В 1-м случае на внутренней поверхности уплотнительных колец будем задавать од-
нородные осевые перемещения uzint :
uz |
|
Γ = ±uzint , ur |
|
Γ = uθ |
|
Γ = 0 , |
(20) |
|
|
|
|||||
1 |
1 |
1 |
|
||||
|
|
|
|
|
|
|
37 |
а во 2-м – однородные окружные перемещения uθint :
uθ |
|
Γ |
= ±uθint , ur |
|
Γ |
= uz |
|
Γ = 0 , |
(21) |
|
|
|
|||||||
1 |
1 |
1 |
|
||||||
исключая оставшиеся составляющие. Знаки «+» и «–» в условиях (21) и (22) позволяют учесть направление поступательного движения и вращения штока.
Решение краевой задачи (6)–(8), (10) о термоупругом деформировании уплотнительных колец с граничными условиями (11), (12), (14)–(20) или (14)–(19) и (21) будем решать численно методом конечных элементов с использованием пакета ANSYS 12.0. При этом на 1-м этапе из решения уравнения Лапласа (10) с граничными условиями (11), (12) определяется стационарное распределение температур внутри уплотнительного элемента. В дальнейшем влияние термических составляющих напряжений учитывается в определяющих соотношениях (8) введением дополнительных слагаемых, содержащих коэффициенты βij . Эти коэффициенты вычисляются по форму-
лам (9) через деформационные характеристики трансверсальноизотропного материала и коэффициенты линейного термического расширения α и αˆ в плоскости изотропии rθ и направлении образующей z УЭ. Несмотря на то, что в рабочем диапазоне температур теплофизические постоянные изменяются, при определении напря- женно-деформированного состояния этим изменением будем пренебрегать. Эту зависимость магистрантам предлагается учесть при выполнении самостоятельной работы.
Численное решение задач об определении напряженно-дефор- мированного состояния изготавливаемых крупносерийными партиями УЭ из наноструктурированного ТРГ позволяет провести оценку начальной прочности и определить степень влияния геометрических размеров уплотнительных элементов и температурных режимов, типа (возвратно-поступательное или вращательное) и направления (в сторону нажимной втулки или в противоположную сторону) движения штока на характер распределения напряжений в точках поперечных сечений.
38
В работе [15] были введены независимые величины
JσI = 12(σrr +σθθ); JσII =σzz ;
JσIII = (σrr −σθθ)2 +4σϕθ2 , JσIV = σ2rz +σθ2z ,
инвариантные относительно ортогональных преобразований, допустимых над цилиндрически трансверсально-изотропным однородным телом с осью симметрии бесконечного порядка z , которые могут быть применены для описания различных механизмов разрушения. На основе независимых инвариантов в работах [5, 6] были сконструированы критериальные условия, позволяющие описать разрушение от растяжения или сжатия в плоскости изотропии
JσI > JσI+cr , |
JσI |
> 0 или |
|
JσI |
|
|
|
> JσI−cr , |
JσI < 0 |
(22) |
|
|
|
||||||||
и продольном направлении |
|
|
|
|
|
|
|
|
|
|
JσII > JσII+cr , |
JσII |
|
|
JσII |
|
> JσII−cr , |
JσII < 0 , |
|
||
> 0 или |
|
|
(23) |
|||||||
от сдвигов в плоскости изотропии |
|
|
|
|
|
|
|
|
||
и от продольного сдвига |
|
JσIII > JσIIIcr |
|
|
(24) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
JσIV > JσIVcr . |
|
|
(25) |
|||||
В неравенствах (22)–(25) содержатся прочностные постоянные
JσI+cr , JσI−cr , JσII+cr , JσII−cr , JσIIIcr и JσIVcr .
Поскольку вычисление независимых инвариантов в пакете ANSYS 12.0 не предусмотрено, магистрантам, выполняющим индивидуальную научно-исследовательскую работу, будет предоставлен специально разработанный и программно реализованный код для подготовки и обработки данных в форматах, совмести-
мых с ANSYS 12.0.
39
6.3. Алгоритм исследования
После подготовки таких разделов работы, как введение, формулировка задач исследования с использованием изложенного выше теоретического материала предлагается следовать изложенному ниже алгоритму. При этом при определении физико-механических свойств графита рекомендуется использовать пакет символьных вычислений Wolfram Research. Mathematica или написать и отладить программу на любом языке программирования.
6.3.1. Прогнозирование упругих модулей кристаллов графита и графена
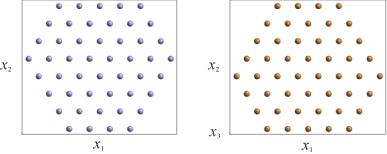
1. Построить геометрическую модель образца с кристаллической решеткой графита/графена (см. рис. 2). Для этого необходимо разработать алгоритм размещения атомов в узлах решетки. Для слоя графена – алгоритм формирования треугольных подрешеток (рис. 9), а для графита – алгоритм построения слоев четного (рис. 10, а) и нечетного типа (рис. 10, б), при чередовании которых формируется образец с заданной структурой. Расстояние a между атомами каждой из простых решеток считать произвольным.
а |
б |
Рис. 9. Строение подрешеток, формирующих монослой графена: а – атомы 1-й подрешетки; б – атомы 2-й подрешетки
40
