
Начертательная геометрия. Инженерная графика электронное учебное из
.pdf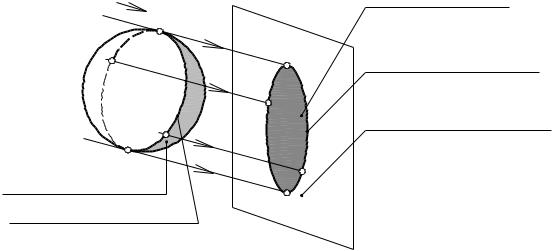
S |
|
Падающая тень |
A |
Ï' |
|
|
|
|
D |
A'T |
Граница падающей |
D' |
òåíè |
|
|
T |
|
C |
|
Плоскость проекций |
B |
C' |
|
Собственная тень |
T |
|
|
|
|
Граница собственной |
B' |
|
T |
|
|
òåíè |
|
|
Рис.25
Затемненная часть освещенного предмета называется собственной тенью предмета.
Падающей тенью называют тень, отбрасываемую предметом на плоскость проекций или другие поверхности.
Контур собственной тени определяется проведением лучевой обертывающей поверхности, касающейся данного предмета. Линия касания и будет контуром собственной тени.
Контур падающей тени от фигуры является тенью от контура собственной тени той же фигуры, то есть совокупностью линий, отделяющих освещенную часть предмета от затененной. Поэтому по границе падающей тени можно определить границу собственной тени и наоборот.
При построении теней в ортогональных проекциях, когда источник света бесконечно удален, необходимо исходить из следующих основных положений:
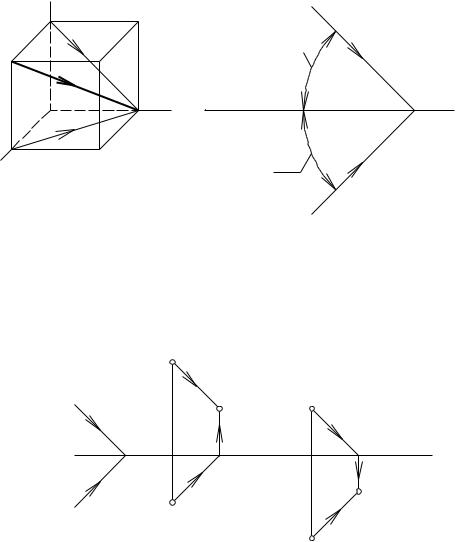
1. Направление лучей света в ортогональных проекциях принимается параллельно диагоналям куба, грани которого параллельны основным плоскостям проекций; благодаря этому проекции лучей света S1 и S2 образуют с осью проекций Ох угол 45° (рис. 26).
2. Тенью точки является след светового луча, проходящего через данную точку. Тень ее окажется на той плоскости проекций, которую световой луч встречает раньше (рис. 27, а, б).
|
z |
S2 |
|
S2 |
|
|
° |
|
|
|
45 |
|
S |
|
|
O |
Ï2 |
|
Ó |
x Ï1 |
x |
S1 |
45° |
|
|
|
|
|
S1 |
|
|
Рис. 26 |
A2
S 2 |
A2Ò |
A2 |
x
S 1 |
A1 |
A1Ò |
A1
аб
Рис. 27
3. Для построения тени от отрезка прямой общего положения на плоскостях проекций необходимо определить тени от двух его точек. Прямая, соединяющая эти точки, и будет тенью от данного отрезка прямой.
При этом могут иметь место три разных случая расположения тени на плоскостях проекций:
а) если все точки отрезка прямой расположены ближе к горизонтальной плоскости проекций, то вся тень от этого отрезка упадет на горизонтальную плоскость проекций (рис. 28, а);
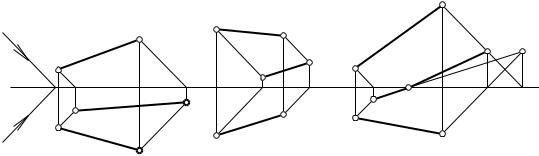
б) если все точки отрезка прямой расположены ближе к фронтальной плоскости проекций, то вся тень от этого отрезка упадет на фронтальную плоскость проекций (рис. 28, б);
в) если одна точка отрезка прямой расположена ближе к горизонтальной плоскости проекций, а другая – к фронтальной плоскости, то тень будет в виде ломаной линии. Для ее построения сначала находят тень отрезка прямой на одну из плоскостей проекций, предполагая, что второй не существует. Полученная тень пересекает ось x в точке Кх, где произойдет преломление тени, и она с одной плоскости проекций перейдет на другую. Установив, какая из двух теней крайних точек отрезка мнимая (L2Т), определяют ее действительную тень на второй плоскости проекций
(рис. 28, в).
|
C2 |
|
|
L2 |
|
S2 |
D2 |
|
|
||
B2 |
M2 |
L2Ò (L1T ) |
|||
A2 |
D2T |
||||
x |
|
C2T |
|
|
|
B1T |
|
|
KX |
||
|
|
|
|||
|
A1T |
D1 |
M1 |
M1T |
|
A1 |
L1 |
||||
C1 |
|
|
|||
S1 |
B1 |
|
|
|
|
|
|
|
|
||
|
а |
б |
|
в |
Рис. 28
Таким образом, тень от линии, падающая на пересекающиеся плоскости (поверхности), является ломаной линией, вершины которой расположены на линиях пересечения плоскостей (поверхностей), а тень от прямой на каждую из пересекающихся плоскостей определяется двумя теневыми точками, расположенными в данной плоскости.
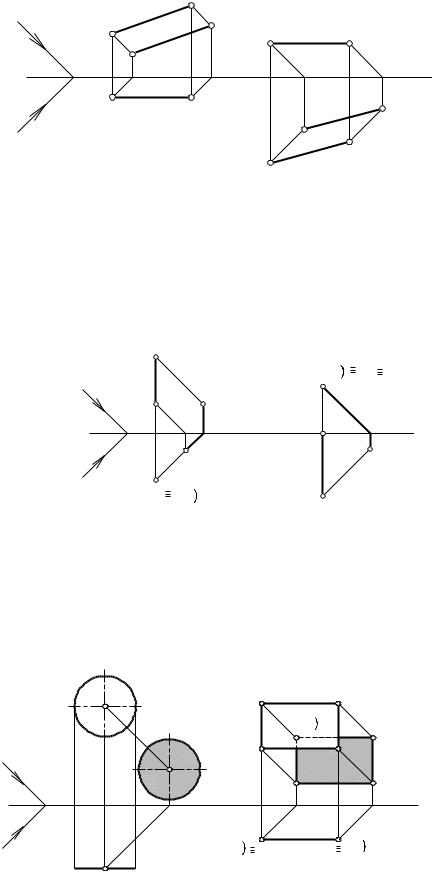
4. Тень от отрезка прямой, параллельной плоскости, параллельна и равна самому отрезку (рис. 29, а, б).
5.Тень от отрезка прямой перпендикулярной плоскости совпадает с проекцией светового луча на эту плоскость (рис. 30, а, б).
6.Тень, падающая на плоскость от точки, лежащей на этой плоскости, совпадает с самой точкой (рис. 30, б).
7.Если плоская фигура, параллельна какой-либо плоскости, то тень от нее на эту плоскость расположена подобно самой плоской фигуре и равна ей (рис. 31).
S2 |
|
B2 |
|
|
|
A2 |
B2Ò |
C |
D |
2 |
|
|
|
|
2 |
|
xA2Ò
A1 |
B |
C |
D1Ò |
|
1 |
|
|
S1 |
|
1Ò |
|
C1 |
|
D1 |
|
|
|
||
|
а |
б |
|
|
Рис. 29 |
|
|
A2 |
|
|
|
|
S2 |
|
(A |
B |
A2Ò |
A2Ò |
2 |
2 |
||
B2 |
|
|
|
|
|
|
|
|
|
x |
|
A1 |
|
|
|
B |
|
B1 Ò |
|
S1 |
1 Ò |
|
|
|
(B |
B |
|
|
|
A |
|
|
||
1 |
1 |
1 |
|
|
а б
Рис. 30
|
O2 |
|
A2 |
|
C2 |
|
|
|
|
||
|
|
|
|
(A2T |
C2T |
|
|
|
|
|
|
S2 |
O2T |
|
B2 |
D2 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
B2T |
D2T |
x |
|
|
|
|
|
|
|
|
|
|
|
S1 |
(B |
1 |
A |
C1 |
(D1 |
|
|
1 |
|
|
|
|
O1 |
|
|
|
|
|
Рис. 31 |
|
|
|
|
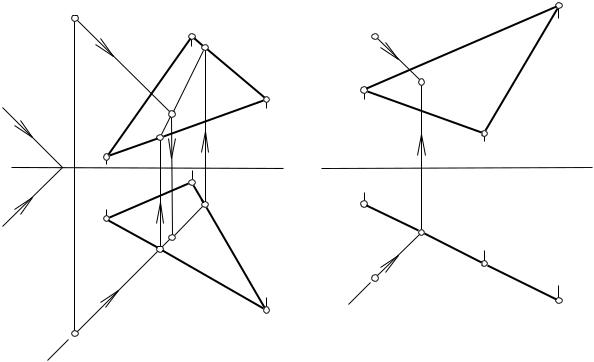
8. Тень от точки на плоскость общего положения можно построить, используя метод вспомогательных лучевых сечений (рис. 32, а). Для этого световой луч, проходящий через точку, заключается во вспомогательную проецирующую лучевую плоскость, затем строится линия пересечения вспомогательной плоскости с заданной плоскостью (поверхностью), после чего определяется точка пересечения светового луча с построенной линией. Тень на проецирующую плоскость строится аналогичным методом
(рис. 32, б).
K2 |
B2 |
K2 |
C2 |
|
|
||
|
22 |
|
|
S2 |
|
A2 |
K2T |
C2 |
|
||
|
|
||
|
|
|
|
12 |
K2T |
|
B2 |
A2 |
|
|
|
x |
|
|
|
A1 |
B1 21 |
A1 |
K1T |
|
|||
S1 |
|
|
|
K1 T |
|
|
|
11 |
|
|
|
|
Σ1 K1 |
B1 |
|
|
|
||
|
C1 |
C1 |
|
|
|
||
Σ 1 K1 |
|
|
|
аб
Рис. 32
9. Иногда при построении теней, падающих от одной геометрической фигуры на другую, применяется метод обратного луча. Суть метода заключается в том, что сначала строятся тени, падающие от обеих заданных фигур на какую-либо плоскость, и выявляются точки пересечения теней от линий, принадлежащих разным фигурам. Затем при помощи обратных лучей (параллельных лучам света, но имеющих обратное направление) эти точки «возвращаются» в пространство на соответствующие контурные линии фигур и с помощью полученных точек определяется искомая тень, падающая от одной фигуры на другую.
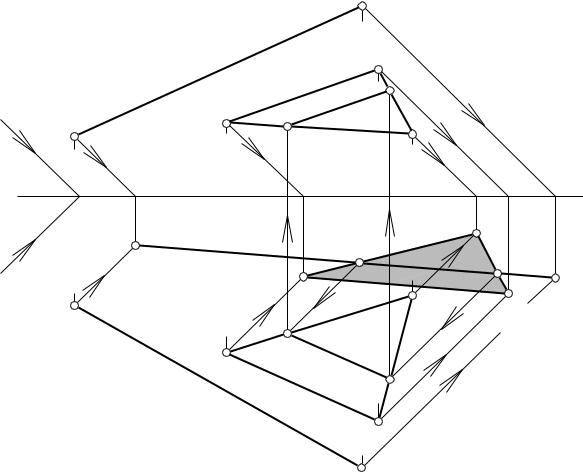
Например, при построении тени от прямой АВ на плоскость треугольника CDE (рис.33) сначала строятся падающие тени прямой АВ и плоскости треугольника CDE на одну из плоскостей проекций. Далее определяют точки пересечения контуров теней между собой 11Т - 21Т. Из этих точек проводятся лучи, направленные в обратном направлении, до пересечения с проекцией С1D1E1 в точках 11Т′ и 2 1Т′. Соединив эти точки, получают проекцию тени от отрезка АВ на горизонтальную плоскость проекций. Перенеся полученные точки на фронтальную плоскость проекций в точки 12Т′ и 22Т′, находят фронтальную проекцию тени от отрезка АВ на плоскость СDE.
|
|
|
B2 |
|
|
|
|
D2 |
|
S2 |
|
|
2'2T |
|
C2 |
|
|
|
|
|
|
|
|
|
|
A2 |
1'2T |
E2 |
|
|
|
|
||
|
|
|
|
|
x |
|
|
|
E1T |
|
A1T |
|
11T |
|
|
|
21T |
||
S1 |
|
C1T |
|
|
|
E1 |
B1T |
||
|
|
|
||
|
A1 |
|
D1T |
|
|
1'1T |
|
|
|
|
C1 |
2'1T |
|
|
|
|
|
|
|
|
|
|
D1 |
|
|
|
|
B1 |
|
|
|
Рис. 33 |
|
|
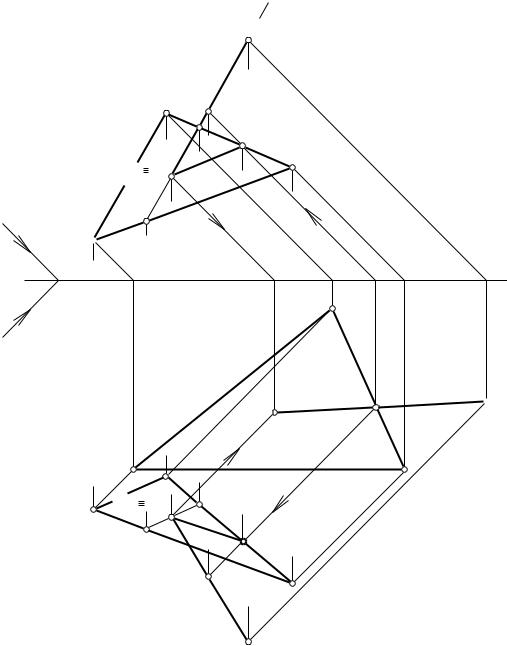
10. Если прямая пересекается с плоскостью, то тень от прямой на эту плоскость проходит через точку пересечения прямой с рассматриваемой плоскостью. Так на рис. 34 тень от прямой DE на плоскость треугольника АВС проходит через точку Е, то есть точку пересечения рассматриваемых прямой и плоскости. Точка Е найдена при помощи вспомогательного лучевого сечения, а точка К – методом обратного луча.
|
Σ2 |
|
D2 |
C2 |
22 K2 |
|
K'2T |
Å'2T E |
B2 |
2 |
S2
A2 1 2
1 2
x
C1T
S1
K1T  D1T
D1T
|
|
|
E1T |
|
A1T |
C1 |
B1T |
|
Å'1T E1 |
21 |
|
A1 |
|
||
|
1 1 |
|
K'1T |
|
|
K1 |
B1 |
|
|
|
|
|
|
|
D 1 |
Рис. 34
2. 1. 1 ЛЕКЦИЯ 2
ТЕНИ ОТ ГЕОМЕТРИЧЕСКИХ ТЕЛ. ПОСТРОЕНИЕ ТЕНЕЙ НА ФАСАДЕ ЗДАНИЯ
Тени от геометрических тел
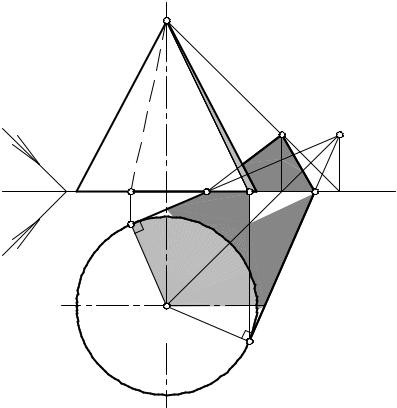
Тень от конуса. Построение тени от прямого кругового конуса, стоящего на горизонтальной плоскости (рис. 35), начинают с построения тени от вершины S, которая падает на фронтальную плоскость проекций. Точку S2Т нельзя соединить с основанием, так как она лежит в другой плоскости. Следовательно, полную тень от конуса находят на той плоскости, в которой лежит основание.
Точку S1Т получают во второй четверти пространства. Далее из этой точки проводят касательные к основанию, используя правило построения касательной к окружности, и получают точки касания А1 и В1. Область, заключенная между касательными, и будет падающей тенью. На оси проекций произойдет перелом тени. От точек перелома тень пойдет в
точку S2Т.
Соединив точки А1 и В1 с вершиной конуса, получают горизонтальную проекцию собственной тени конуса, после чего определяют ее фронтальную проекцию.
S′
2
S |
S2Ò (S 1Ò ) |
|
2 |
A2  B2
B2 
A1
S1
S′1 

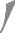
B1
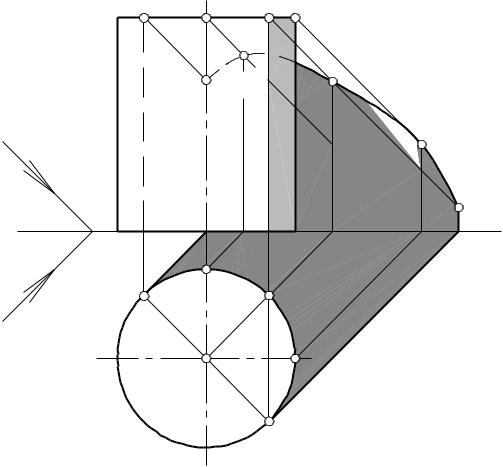
Рис. 35
Тень от цилиндра. Построение тени от прямого кругового цилиндра, стоящего на горизонтальной плоскости (рис. 36), начинают с определения контура собственной тени цилиндра.
Касательные к основаниям цилиндра отделяют освещенную часть цилиндра от неосвещенной. Следовательно, следует построить тень от дуги основания 1-2-3-4-5 и образующих, проходящих через точки 1 и 5.
Тень от образующих на горизонтальной плоскости проекций совпадает с проекциями светового луча. Тень от дуги основания 1-2-3-4-5 строится по точкам и упадет на фронтальную плоскость проекций. Перелом тени произойдет на оси проекций.
Тень от шара. Если описать цилиндр как обертывающую поверхность вокруг шара (оси этих поверхностей вращения совпадают), то касание произойдет по окружности основания цилиндра, которая и будет являться контуром собственной тени шара (рис. 37).
12 22 (32) 52 42
52 42
32Ò
(12Ò) (22Ò)
S2  42Ò
42Ò
52Ò
1 1 |
21 |
31 |
S1 |
|
41 |
|
|
51
Рис. 36
5
4 
O
3
3
0 °
2
1 11 12
11 12
Рис. 37
6
4
5 °
10
7
8
9
Построение контура собственной тени шара может быть выполнено графически. На фронтальной проекции шара проводят его вертикальный и горизонтальный диаметры и два диаметра под углом 45 °. Диаметр 1-7 на контуре шара даст две точки 1 и 7, принадлежащие контуру собственной тени. Эти точки делят контур собственной тени на видимую и невидимую части. Линия 1-7 является большой осью эллипса. Далее из точек 1 и 7 проводят линии, параллельные горизонтальному диаметру, до пересечения с вертикальным и получают точки 5 и 11, а, проведя линии параллельно вертикальному диаметру, до пересечения с горизонтальным, получают точки 3 и 9. Затем находят малую ось эллипса, проводя из точки 1 линию под углом 30° к большой оси до пересечения с направлением малой оси; получают точку 10, а далее – точку 4, отложив отрезок О -4, равный О -10.
Для построения точек 6, 8, 12, 2 из точек 4 и 10 проводят линии параллельно горизонтальному диаметру до пересечения с большой осью эллипса и получают точки А и В. Соединяют точки 4, А, 10, В и получают квадрат. Продолжив стороны квадрата за точку А вверх и вправо и за точку В влево и вниз и отложив на этих прямых отрезки, равные половине стороны квадрата, получают точки 12, 2, 6, 8. Соединив последовательно построенные 12 точек, получают контур собственной тени на шаре в виде эллипса.
Аналогичные построения можно выполнить и на горизонтальной проекции шара. Далее строят падающую тень от контура собственной тени. Чтобы получить проекцию окружности касания лучевого цилиндра к
