Телемеханика и связь

пульсу 3 и т.п. Команда ¹ 12 будет передаваться комбинацией импульсов 1 и 2, команда ¹ 34 – комбинацией импульсов 3 и 4 и т.п. Число возможных сообщений при таком способе кодирования N = 10n, где 10 – основание кодовой комбинации, а n – ее длина, или длина слова. Чтобы получить N = 999, следует взять n = 3. Однако в десятичной системе счисления число импульсных признаков оказывается излишне большим, что может привести к ошибкам при различии команд. Наличие помех изменяет амплитуду импульсов.

Число импульсных признаков можно уменьшить до двух, применяя для нумерации команд двоичную систему счисления. Но при этом возрастает длина слова или число разрядов n. В нашем примере для передачи 1000 сообщений n должно быть не менее 10, тогда N = 210 = 1024. Таким образом, в общем случае

ãäå q – основание кода, или число признаков.

Если число признаков q = 2 (0 и 1, а и б), то такие коды называют двоичными (бинарными), или двухпозиционными. Коды, у которых q & 3, являются многопозиционными, или недвоичными – небинарными (троичными, четверичными и т.п.).

Оказывается, надежность передачи значительно увеличивается при уменьшении числа и усилении различия признаков, несмотря на увеличение длины слова. Поэтому в настоящее время применяют, за редким исключением, двоичные коды (q = 2). Импульсные признаки для передачи таких кодов могут быть довольно разнообразными (см. табл. 2.1). Так, 1 может передаваться, например, или наличием импульса с амплитудой A, или импульсом длительностью, а 0 – отсутствием импульса или импульсом длительностью 1. Могут быть использованы и другие импульсные признаки.

Комбинации двоичного кода можно записать также буквами. Например, комбинация 10101 запишется как абаба. Таким образом, любая кодовая комбинация содержит определенный набор элементов или символов (1 и 0, а и б), которые называются буквами алфавита, а весь набор букв образует алфавит кода. Если для двоичного кода алфавит состоит только из двух символов, то для троичного кода их число увеличивается до трех (а, б, в, и 1, 2, 3), а в десяти- чном коде оно равно десяти.

31

ELIB.PSTU.RU

щие системы счисления вообще и двоичную систему в частности, поскольку возникшие на ее основе двоичные коды получили наибольшее распространение в телемеханике.

Построение любой системы счисления начинается с выбора ее основания, т.е. того количества цифр, из комбинации которых можно полу- чить любое число. Сущность десятичной системы счисления заключается в том, что, располагая десятью цифрами (от 0 до 9), мы можем записать любое из чисел. Десять – уже двузначное число, которое записывается двумя разрядами: единицей в разряде десятков и нулем в разряде единиц. По этому принципу можно построить систему счисления из любого числа цифр, например, из восьми (табл. 2.2). В той же таблице приводится так называемая римская (пятеричная) система, которая позволяет объяснить, как строятся различные системы счисления.

В основу двоичной системы положены лишь два числа: 0 и 1. Десятичное число 2 передается как 10 (заметим, что это сочетание 1 и 0 в десятичной системе выражало число 10, в восьмеричной – 8, в пятеричной

– 5). Число 3 может быть представлено как сумма 2 + 1, т.е. 10 + 1 = 11, число 22 = 4 – êàê (10)2 = 100, число 5 – как 100 + 1 = 101 и т.д.

Широко используемая десятичная система счисления имеет слишком много цифр для запоминания и воспроизведения в электронных устройствах. Восьмеричную систему счисления применяют при составлении программ, так как запись по ней примерно в три раза короче, чем по двоичной системе (23 = 8).

Ò à á ë è ö à 2 . 2

Системы счисления

33

ELIB.PSTU.RU

Двоичная система счисления нашла широкое применение в вы- числительной технике, где за счет использования в ней только двух цифр (0 и 1) легко осуществляются арифметические операции. Схемная реализация операции с двоичными числами проста. Это объясняется тем, что многие устройства, используемые в вычислительной технике и телемеханике, являются устройствами релейного действия (электромеханические реле, триггеры, лампы тлеющего разряда, магнитные элементы с прямоугольной петлей гистерезиса и др.), т.е. обладают двумя устойчивыми состояниями, соответствующими 1 или 0.

Запись кодовых комбинаций в виде многочлена. Любое число в системе счисления с основанием X можно представить в виде многочлена. Так, n-разрядное число запишется в виде

ãäå a – цифровые знаки, имеющие значения от 0 до X – 1.

В десятичной системе счисления X = 10, à – это цифры 0, 1, 2, ..., 9. Например, четырехзначное число 4357 запишется как

F(10)= 4 103 + 3 102+ 5 101+ 7 100 = 4357.

В двоичной системе счисления, где Õ = 2, коэффициенты à принимают только одно из двух значений: 1 или 0, тогда двоичное число 10101001 в десятичном эквиваленте запишется таким образом:

F(10) = 1 27 + 0 26 + 1 2 5 + 0 24 + 1 23 + 0 22 + 0 21 + 1 20 =169

или в виде многочлена

Q(X ) = 1 X 7 + 0 X 6 + 1 X 5 + 0 X 4 + 1 X 3 + 0 X 2 + 0 X 1 + 1 X 0.

Опуская члены с коэффициентами, равными нулю, и не выписывая единицы как множитель, получаем

Q (X ) = X 7 + X 5 + X 3 + 1.

Таким образом, члены многочленов записываются только при наличии коэффициента единицы. При этом степень соответствующего числа многочлена берется уменьшенной на единицу по отношению к номеру разряда в двоичной записи, отсчитанному справа

34

ELIB.PSTU.RU

налево. Так, первым записывается X 7, несмотря на то что этот член в двоичной записи находится в восьмом разряде.

Сложение. Над многочленами можно производить все алгебраи- ческие операции. Обычное сложение с переносом числа в высший разряд здесь неприменимо, так как это может привести к образованию более высокого разряда, чем принято в данном коде, что недопустимо. Поэтому применяется так называемое сложение двоичных чисел по модулю два, обозначаемое знаком (. При двух слагаемых правила сложения следующие: 0 ( 0 = 0; 0 ( 1 = 1; 1 ( 0 = 1; 1 ( 1= 0.

При сложении многозначных чисел складывают разряды, занимающие одинаковые места. При этом сложение сводится к сложению только коэффициентов при членах совпадающих степеней.

Если складываются несколько чисел, то четное число единиц в сумме дает нуль, а сумма нечетного числа единиц приравнивается к единице. При этом порядок сложения безразличен. Иногда в результате сложения нескольких чисел сумма выражается меньшим двоичным числом, чем какое-либо из слагаемых. Для примера произведем сложение следующих многочленов:

X 6 + X 5 + X 3 + X 2 +1,

X 5 + X 4 + X 2,

X 6 + X 5 + X 4 + X 3 + X 2 + X 1 + X 0.

Выразим эти многочлены в двоичных числах и, расположив их соответствующим образом в столбцы, произведем сложение:

(

X 6 + X 5 + X 4 + X 3 + X 2 + X + 1 – 1111111

0 + X 5 + 0 + 0 + X 2 + X + 0 – 0100110.

Умножение. Для того чтобы при умножении многочленов не увеличилась разрядность степени многочлена выше заданной, производят символическое умножение, или умножение в конечном

35

ELIB.PSTU.RU

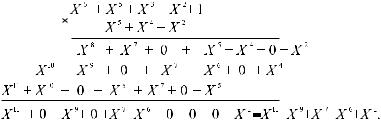
поле двоичных чисел, состоящее из двух этапов. Первый этап заключается в умножении многочленов по обычным правилам алгебры, за исключением сложения, которое производится по модулю 2. Перемножим два многочлена:

Произведем теперь умножение многочлена на X n. Например,

(X 5 + X 4 + X 2) Õ 3 = Õ 8 + Õ 7 + Õ 5.

В результате умножения степень каждого члена многочлена повысилась на ï. В двоичной форме записи 110100 ) 1000 = 110100000.

Таким образом, умножение многочлена на X n означает приписывание справа ï нулей. Как следует из примеров, перемножение дало увеличение степени многочлена, т.е. увеличение разрядности кодовой комбинации.

Если максимальная степень полученного многочлена превышает заданную разрядность, то необходимо произвести второй этап символического умножения, заключающийся в делении полученного произведения на заранее заданный многочлен. При этом окон- чательным результатом является остаток от деления. Заметим, что в рассматриваемых далее случаях кодирования при умножении многочленов не придется прибегать ко второму этапу символического умножения.

Деление. Предположим, что надо разделить многочлен X 8 + X 7 + X 5 + X 4 + X 2 + l, что соответствует комбинации 110110101, на многоч- лен X 5 + X 3 + X + 1, который в кодовой записи имеет вид 101011. Произведем деление, пользуясь многочленной формой записи. При этом вместо вычитания будем производить сложение по модулю 2, так как эти операции тождественны:

При делении в двоичной системе счисления делитель умножается на частное и подписывается под делимым так, чтобы совпадали старшие разряды. В частное записывается единица. Для нахождения пер-

36

ELIB.PSTU.RU

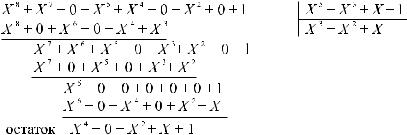
вого остатка из делимого вычитается делитель (что эквивалентно их сложению по модулю 2) и к остатку справа сносится очередной разряд делимого. Далее под первым остатком снова подписывается делитель и в частное приписывается еще одна единица, если число разрядов в остатке равно числу разрядов делителя. В противном случае в частном записывается нуль и к остатку подписывается очередной член делимого. Деление продолжается до тех пор, пока степень остатка не станет меньше степени делителя, т.е. число разрядов остатка не окажется меньше, чем число разрядов делителя.

Перенос слагаемых. Понятие отрицательного элемента (цифры) при операциях в конечном поле двоичных чисел отсутствует, так как это привело бы к увеличению признаков с двух до трех, т.е. к троич- ной системе счисления. Поэтому перенос слагаемых из одной части равенства в другую производится без изменения знака. Например, справедливо как выражение (X 4 + Õ + 1) + (Õ 3 +Õ) = Õ 4 + Õ 3 +1, так и выражение, отличающееся тем, что второе слагаемое левой части перенесено в правую без изменения знака, т.е. X 4 + X + 1 = (Õ 3 + X) + + (X4 + X 3 + 1). Справедливость этих равенств проверяется сложением по модулю 2 одночленов с одинаковыми степенями.

2.3. Непомехозащищенные коды

Особенностью непомехозащищенных кодов является наличие кодовых комбинаций, которые отличаются друг от друга лишь в одном разряде. Типичным кодом такого типа является двоичный код на все сочетания, представленный в табл. 2.2 (столбец 4). Здесь, например, комбинации 0010 и 0011 отличаются друг от друга лишь в младшем разряде. Если помеха исказит первую комбинацию,

37

ELIB.PSTU.RU

то будет принят сигнал 0011 и будет неясно, то ли принята первая искаженная комбинация, то ли вторая неискаженная. Можно найти еще ряд комбинаций в том же коде, которые отличаются друг от друга только в одном разряде. Например, комбинации 0101 и 0111 отличаются во втором разряде, комбинации 0011 и 0111 – в третьем разряде, а комбинации 1110 и 0110 – в четвертом разряде. В то же время в этом же коде есть ряд комбинаций, которые отличаются друг от друга в двух разрядах и более. Например, комбинации 1111 и 0001 отличаются в трех старших разрядах. Однако, поскольку для этих же комбинаций имеются такие соседние комбинации, которые отличаются от каждой из них в одном разряде (0111, 1110, 1101, 1011 для комбинации 1111 и 0000, 0011, 0101, 1001 для комбинации 0001), в целом это делает двоичный код на все сочетания непомехозащищенным.

Таким образом, непомехоустойчивыми (или непомехозащищенными) кодами называют коды, в которых искажение одного разряда кодовой комбинации не может быть обнаружено. Иногда их называют обыкновенными кодами. Рассмотрим примеры двоич- ных непомехозащищенных кодов.

Двоичный код на все сочетания. Кодовые комбинации этого кода соответствуют записи натурального ряда чисел в двоичной системе счисления. Общее число комбинаций

Единично-десятичный êîä. Каждый разряд десятичного числа записывается в виде соответствующего числа единиц. При этом разряды разделяются интервалами. Этот код неравномерный, хотя и может быть преобразован в равномерный путем приписывания

âкаждом разряде слева нулей, доводящих общее число символов

âкаждом разряде до 10. Например число 234 при записи его равномерным единично-десятичным кодом оно имеет вид 0000000011, 0000000111, 0000001111.

Двоично-десятичный êîä. Каждый разряд десятичного числа записывается в виде комбинации двоичного кода. Например, цифра 9 в двоичной системе запишется как 1001, а цифра 3 – как 0011. Поэтому число 399 при записи двоично-десятичным кодом будет иметь вид 001110011001.

38

ELIB.PSTU.RU

Числоимпульсный код. Иногда его называют единичным (или унитарным) кодом. Кодовые комбинации отличаются друг от друга числом единиц. Очевидно, что

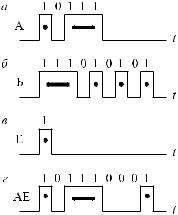
Код Морзе. Этот код относится к числу неравномерных кодов, в которых кодовые комбинации отличаются различной длительностью. В коде Морзе сигналы (буквы, цифры) передаются в виде тире и точек.

мерно 9,5 . Заметим, что то же число сигналов можно было бы передать шестиэлементным равномерным ко-

дом, где средняя длина кодовой комбинации равна 6 . Различная длина кодовых комбинаций при передаче букв и цифр является недостатком телеграфного кода Морзе, впервые примененного в 1844 году.

2.4. Помехозащищенные (корректирующие) коды

Основные понятия. Помехозащищенными (или корректирующими) называются коды, позволяющие обнаружить и исправить ошибки в кодовых комбинациях. Отсюда и деление этих кодов на две большие группы: 1) коды с обнаружением ошибок; 2) коды с обнаружением и исправлением ошибок.

39

ELIB.PSTU.RU