Физика сборник олимпиадных задач с примерами их решений

Задача 1. Угол разлета шариков одинаковой массы при абсолютно упругом нецентральном ударе равен 90° (докажите). Поэтому, если шарик А очевидно летит горизонтально, то шарик В должен лететь вертикально. Можно сделать вывод, что шарики – не точечные массы (!), их радиус равен двум клеточкам. Дальнейшее решение труда не представляет.

Задача 3. Найдите, что в момент отрыва стержня от опоры

и направлена под углом φ к горизонту, причем cos ϕ = 2 . Далее

3

шарик будет совершать свободное падение, т.е. двигаться по параболе. Расчеты стандартные.

Замечание. Интересно, что величина скорости падения

Задача 4. 1) При движении перемычки в магнитном поле на его концах возникнет разность потенциалов, или, другими словами, в цепи возникнет ЭДС индукции ε i = vBd , потечет ток

по правилу Ленца направленная в сторону, противоположную

вает тот факт, что скорость перемычки падает, т.е. dv < 0 ) mdυ = − B2 d 2υ dt, υ dt = ds – малое перемещение перемычки,

41

получаем ответ на первый вопрос. 2) Для того, чтобы ответить на второй вопрос, нужно вернуться к уравнению (*). Это дифференциальное уравнение с разделяющимися переменными. После интегрирования получаем зависимость скорости перемычки

Замечание. а) В отсутствие трения скорость перемычки будет асимптотически приближаться к нулю по экспоненте, но никогда не будет равна нулю точно. Однако суммарный путь, пройденный перемычкой, конечен, т.е.

стремится к значению s. б) Из ответов задачи следует интересная связь: s =υ 0te .

Задача 5. Ракеты будут двигаться по эллиптическим траекториям (см. рис. 1), в фокусе которых находится центр Земли. Максимальное расстояние между ракетами будет равно Lmax = 2r. Наибольшее расстояние r каждой из ракет от центра Земли можно най-

ти при помощи закона сохранения момента импульса относительно оси, проходящей через центр Земли и перпендикулярной плоскостям орбит mυ 0 R = mυ r, а также закона сохранения энер-

М – масса Земли. Решая совместно последние два уравнения, находим r. При записи окончательного ответа удобно воспользоваться выражением для ускорения свободного падения вблизи

поверхности Земли g = GM .

R2

42

Первый тур (2009 г.)

5. 1) на шариках гантельки возникнут индуцированные за-

Задача 2. Скорость падения мальчика на доску υ 0 = 2gh.

Разумно предположить, что столкновение мальчика с доской неупругое, тогда закон сохранения момента импульса системы относительно оси вращения будет иметь вид mυ 0 2l = mυ 1 2l + Mυ 2 l ,

где υ 1 и υ 2 – скорости мальчика и мужчины сразу после соударения. Подчеркнем, что мальчик сразу после соударения имеет ненулевую скорость! Скорости υ 1 и υ 2 выражаются через угловую

скорость вращения доски: υ 1 = ω 2l, υ 2 = ω l. Далее, т.к. доска расположена невысоко над полом, конец доски с мальчиком ударяется о землю (при этом доска остается практически горизонтальной), вследствие этого резко останавливается и конец доски, на которой стоит мужчина. А мужчина по инерции продолжает движение вверх с начальной скоростью υ 2 и поднимается на

высоту = υ 2

H 2 . 2g

Задача 3. См. замечания к задаче № 3 первого тура 2003 г. Задача 4. 1) Для ответа на первый вопрос достаточно за-

43

полное время торможения стержня. Здесь важно правильно рассчитать момент сил тре-

ния, действующий на стержень: Мтр = µmgl . 4

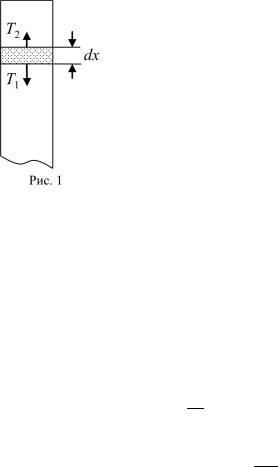
3) Рассмотрим малый элемент стержня массой dm и длиной dx, удаленный на расстояние х от его центра. Вдоль оси стержня на этот элемент с разных сторон действуют две части

стержня с силами Т1 и Т2 (см. рис. 1). Сила Т1 больше силы Т2, поскольку нормальное ускорение элемента dx направлено к центру стержня (поэтому понятно, что чем ближе к центру стержня, тем сила натяжения будет больше, сила натяжения на краю стержня равна нулю). Далее dT = T2 − T1 – результирующая сила,

действующая на элемент вдоль оси стержня или, другими словами, приращение силы натяжения стержня при смещении на расстояние dx от оси стержня (dx и dT – разных знаков, dx > 0, dT < 0). Второй закон Ньютона для элемента в проекции на ось стержня будет иметь вид dmω 2 x= − dT . Массу элемента выра-

жаем через его длину: dm = m dx , подставляем в уравнение вто- l

рого закона Ньютона, интегрируем, берем угловую скорость

к ответу.

Задача 5. 1) На шариках гантельки возникнут индуцированные заряды: на ближнем шарике отрицательный (–qi), на дальнем шарике положительный qi. Поскольку отрицательно заряженный шарик ближе к заряду Q, гантелька будет притягиваться к заряду Q. 2), 3) Результирующая сила, действующая на

44

задачи – оценить индукционные заряды на шариках. В равновесии электрическое поле внутри металла равно нулю. Оценку зарядов можно сделать из условия равенства нулю напряженности электрического поля в центре гантельки, считая, что индуцированные заряды расположены на шариках и являются практически точечными. Подчеркнем, что реальное распределение индуцированных зарядов на гантельке таково, что поле не только в центре, но и внутри всей гантельки равно нулю. Поэтому расчеты носят характер оценочных. Итак, поле в цен-

Сделаем два замечания: а) физически необоснованной является попытка оценить индукционные заряды исходя из равенства нулю результирующей кулоновской силы, действующей на один из индукционных зарядов со стороны другого индукционного заряда и заряда Q (подумайте, почему). Хотя это решение тоже приводит к результату F~1/r5. б) Доказать, что сила обратно пропорциональна пятой степени расстояния, можно из предположения, что индуцированный дипольный момент гантельки в поле напряженностью Е прямо пропорционален Е: рi = α E, где α – характеристика гантельки, аналогичная поня-

тию поляризуемости для молекул. Сила взаимодействия между

45

Задача 2. Пусть φ – угловой путь бусинки, ω – ее угловая скорость. Из второго закона Ньютона следует дифференциальное

уравнение для функции ω (ϕ ) : (ω 2 )′+ 2µω 2= − 2g (sin ϕ + µcos ϕ ).

R

Подчеркнем, что производная от ω2 берется по углу φ. Решая это

ω (0) и υ 0 = ω 0 R . Анализ результата показывает, что уже при

µ = 0,18 бусинка не сможет достичь горизонтального диаметра ни при какой начальной скорости.

Задача 3. Законы сохранения импульса и энергии для системы из двух тел (шарика и стержня) имеют вид

46

и центра масс стержня после соударения, ω – искомая угловая скорость вращения стержня после соударения. Во время соударения на конец стержня действует сила F со стороны шарика. Уравнения динамики для центра масс стержня и вращательного движения стержня в процессе соударения

в систему (*) и, решая систему, приходим к ответу.

Задача 4. Вообще говоря, ответ получается не только при условии малости колебаний, но и при условии достаточной малости деформации пружин в положении равновесия.

Задача 5. Выберем систему координат: начало координат

уравнение на оси координат, получаем систему дифференциальных уравнений:

47

вычисления опускаем ввиду их громоздкости, лишь отметим, что при вычислении интеграла следует учесть малость вели-

порядка малости.

Замечания. а) Со временем движение частицы установится ( e−β t → 0 ) и будет равномерным с компонентами скорости:

б) Рекомендуем решить задачу при отсутствии сопротивления среды. Тогда при нулевой начальной скорости частица будет двигаться по циклоиде, а в инерциальной системе отсчета,

48

Второй тур (2008 г.)

координат совпадает с начальным положением точки 1. Ось Оx направлена в сторону движения точки 1, ось Оy направлена к начальному положению точки 2.

мент времени t, k – некоторая константа, характеризующая ин-

49

и после интегрирования получаем: r = r0 + ρA t = r0 + kt. Уравне-

ние Мещерского (описывающее движение тел с переменными массами) в нашем случае можно представить в виде

d (mυ ) = mg . dt

Подставляем в данное уравнение выражение для массы ка-

гаться равноускоренно с ускорением a = g . б) Другой интерес- 4

ной моделью падения капли является модель, в которой капля, падая под действием силы тяжести, неупруго сталкивается с неподвижными каплями, в результате чего растет ее радиус. В этом случае изменение радиуса капли будет прямо пропорционально пройденному каплей пути, а не времени. Тем не менее в случае r0 = 0 падение тоже будет равноускоренным, толь-

ко с ускорением a = g . Советуем читателям получить эти ре- 7

зультаты самостоятельно.

Задача 3. Как только цилиндр попадет на шероховатую поверхность, он начнет раскручиваться за счет момента силы трения. Угловая скорость вращательного движения ω будет расти, скорость центра масс υ c будет уменьшаться. Как только вы-

полнится соотношение υ c = ω R, сила трения скольжения исчез-

нет и установится качение без проскальзывания. Произвольное движение твердого тела можно описать при помощи двух векторных уравнений: уравнения, описывающего движение центра

50