656310

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ

«ВОРОНЕЖСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ»

МЕХАНИКА

Часть 4

ДИНАМИКА ТВЕРДОГО ТЕЛА

Практикум

Составители: Е.С. Рембеза, В.И. Кукуев

Воронеж Издательский дом ВГУ

2016

1

Утверждено научно-методическим советом физического факультета 28 сентября 2016 г., протокол № 7

Рецензент – д-р физ.-мат. наук, профессор Е.Н. Бормонтов

Практикум подготовлен на кафедре общей физики физического факультета Воронежского государственного университета.

Рекомендован студентам 1-го курса очной и 2-го курса очно-заочной форм обучения физического факультета

Для направлений: 03.03.02 – Физика, 03.03.03 – Радиофизика,

11.03.04 – Электроника и наноэлектроника, 14.03.02 – Ядерная физика и технология

2

ЛАБОРАТОРНАЯ РАБОТА М-4.1

ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ ТВЕРДОГО ТЕЛА МЕТОДОМ КРУТИЛЬНЫХ КОЛЕБАНИЙ

Цель работы: экспериментальное определение моментов инерции некоторых твердых тел относительно оси, проходящей через центр масс. Проверка теоремы Гюйгенкса-Штейнера.

Приборы и принадлежности: трифилярный подвес, набор тел, секундомер, осветитель.

ВВЕДЕНИЕ

Моментом инерции I материальной точки относительно некоторой оси называется физическая величина, равная произведению массы m этой точки на квадрат расстояния r до этой оси

I mr2 ;

для системы n материальных точек

n

I mi ri2 ;

i 1

для сплошного твердого тела

I r2dm r2dV ,

где dm = ρdV – масса элементарного участка тела, dV – объем этого участка, ρ – плотность в данной точке тела, r – расстояние участка до рассматриваемой оси. Интегрирование ведется по всей массе или по всему объему тела. Аналитическое выражение таких интегралов возможно только в простейших случаях тел правильной геометрической формы. В более сложных случаях интегралы могут быть рассчитаны численными методами. Наиболее просто вычисляются моменты инерции симметричных тел относительно оси симметрии, проходящей через центр масс.

Рассмотрим пример вычисления момента инерции тонкого однородного стержня относительно оси вращения, перпендикулярной продольной оси данного стержня (рис. 1).

Пусть длина стержня равна l, а площадь поперечного сечения – S. Ось вращения проходит на расстоянии l1 от одного конца стержня и на расстоянии l2 от другого. Очевидно, что l1 + l2 = l. Вырежем мысленно в стержне перпендикулярно его продольной оси диск толщиной dr на расстоянии r от оси вращения. Масса этого диска будет dm. Тогда по определению элементарный момент инерции диска равен:

dI r2dm r2dV r2 Sdr ,

3

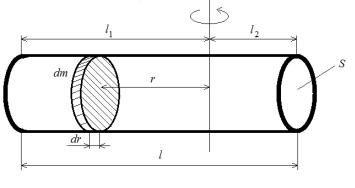
Рис. 1. Вычисление момента инерции однородного стержня

Для определения момента инерции всего стержня нужно провести интегрирование по радиусу вращения r, когда он изменяется от 0 до l1 или l2 :

Если ось вращения проходит через один из концов стержня, например, правый, то l2 = 0, а l1 = l. Тогда момент инерции стержня будет равен:

I 13 Sl3 или I 13 Ml2 .

Моменты инерции твердых тел зависят от распределения массы тела относительно заданной оси. Приведем результаты вычисления моментов инерции для некоторых часто встречающихся тел (во всех примерах М – полная масса тела). Ось вращения проходит через центр масс.

Сплошной цилиндр радиуса R – I 12 MR2 .

Полый цилиндр, R1 и R2 – внешний и внутренний радиусы –

I 12 M R12 R22 .

Шар радиуса R – I 52 MR2 .

Момент инерции тела относительно любой оси, не проходящей через центр масс, может быть определен по теореме Гюйгенса-Штейнера: I = I0 + + ma2, где I0 – момент инерции тела относительно параллельной оси, проходящей через центр масс, a – расстояние между осями. То есть, момент инерции тела относительно какой-либо оси равен моменту инерции тела относительно параллельной оси, проходящей через центр масс, сложенному с произведением массытеланаквадратрасстояниямеждупараллельнымиосями.

4

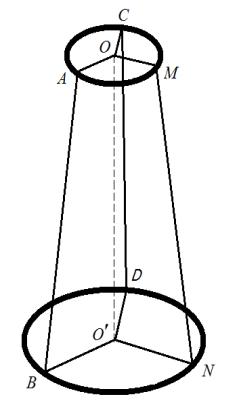
ОПИСАНИЕ УСТАНОВКИ И МЕТОДА ИЗМЕРЕНИЙ

Рис. 2. Трифилярный подвес

Трифилярный подвес (рис. 2) состоит из трех нерастяжимых нитей длиной l, на которых подвешены два диска с радиусами r и R (R > r). Нижний диск – платформа – может совершать крутильные колебания вокруг вертикальной оси ОО', перпендикулярной платформе и проходящей через ее центр масс, который при колебаниях перемещается вдоль оси вращения. Положение трифилярного подвеса можно однозначно задать углом поворота φ платформы BDN вокруг оси ОО'. При малых углах отклонения от положения равновесия платформа будет совершать гармонические колебания по закону

где φ0 – максимальный угол отклонения платформы (амплитуда колебаний), Т – период колебаний. Если пренебречь работой сил трения, то можно записать закон сохранения механической энергии для колеблющейся платформы: потенциальная энергия, которую платформа приобретает при отклонении от положения равновесия за счет поднятия центра масс на высоту h, переходит в кинетическую энергию вращения при прохождении положения равновесия

5

где ω0 – максимальное значение угловой скорости ddt . Из (1) находим ω0 :

T

Высоту h можно найти из условия нерастяжимости нитей АВ, СD и NM. При колебаниях платформы длина нитей

не изменяется. Для выражения длины нити удобно связать прямоугольную систему координат с неподвижным диском, поместив начало координат в центр диска О и направив ось Х вдоль радиуса ОА, ось Z – вдоль оси вращения вниз, ось Y – перпендикулярно к ним. Тогда для нити АВ координаты точки А, которые в процессе колебаний не изменяются, равны: xА = r,

yА = 0, zА = 0. Координаты точки В в положении равновесия имеют значения

xВ(0) = R, yВ(0) = 0, zВ(0) = l.

При повороте нижней платформы на максимальный угол φ0 коорди-

наты точки В будут: xВ = R cos φ0, yВ = R sin φ0, zВ = l - h. Запишем условие постоянства длины нити АВ:

6

Подставляя (6) в (4), получим рабочую формулу для вычисления момента инерции:

Следует учесть, что m – масса платформы и тела, которое на ней лежит, то есть m = mпл + mт, I – момент инерции платформы с телом. Используя свойство аддитивности момента инерции, можно определить момент инерции тела, измерив предварительно момент инерции ненагруженной платформы:

где погрешность Iпл+т момента инерции системы платформа-тело вычисляется следующим образом:

Для вычисления погрешности Iпл момента инерции пустой платформы, очевидно, следует в формулах (11) положить mт = 0 и mт = 0.

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

Задание 1. Определить момент инерции ненагруженной платформы.

1.Привести платформу во вращательное движение, для этого плавно натянуть шнур, расположенный слева от установки, и резко его отпустить. Колебания должны быть такими, чтобы смещение светового зайчика не превышало 40–50 см в обе стороны шкалы.

2.Измерить время 30–50 полных колебаний. Опыт повторить 5 раз.

Tnt .

4.По формуле (9) вычислить момент инерции платформы.

7

5. Вычислить погрешность измерения момента инерции.

Задание 2. Определить момент инерции кольца (или другого тела по указанию преподавателя)

относительно оси симметрии

1.На платформу трифилярного подвеса положить кольцо так, чтобы центр кольца совпал с центром масс платформы. Для этого воспользоваться концентрическими окружностями, нанесенными на платформе, центр которых совпадает с центром масс платформы.

2.Повторить действия согласно пунктам задания 1 для нагруженной платформы. При этом момент инерции нагруженной платформы вычисляется по формуле (7), где m = mпл + mк , а момент инерции кольца по формуле (8).

Задание 3. Проверка теоремы Гюйгенса-Штейнера

1.Определить момент инерции стержня Iст относительно оси, проходящей через его центр масс перпендикулярно продольной геометрической оси. Для этого положить стержень на платформу так, чтобы его центр масс совпал с центром масс платформы, используя концентрические окружности, нанесенные на платформе.

2.Повторить действия согласно заданию 2 и вычислить момент инер-

ции Iст стержня и погрешность Iст его измерения, используя соответственно формулы (8), (10), (11), в которых mт = mст.

3.Определить момент инерции Iа стержня относительно оси, находящейся на расстоянии а от центра масс стержня. Для этого на платформу трифилярного подвеса положить 2 одинаковых стержня, для которых уже

определен Iст, симметрично относительно центра масс платформы на расстоянии 2а друг от друга (расстояние между центрами масс стержней измеряется линейкой так, чтобы она проходила через центр масс платформы), 2а = 15–20 см (по указанию преподавателя).

4.Повторить действия согласно пунктам задания 2 и вычислить момент инерции двух стержней относительно оси вращения платформы по формуле

I2ст Rrg mпл 2mст T 2 Iпл .

4 2l

5. Вычислить момент инерции Iа одного стержня, находящегося на

6. Вычислить погрешность суммы I0 + ma2. Представить отдельно левую и правую части проверяемого равенства Iа = I0 + ma2 с указанием их погрешностей. Если указанные доверительные интервалы пересекаются, то

8

справедливость теоремы Гюйгенса-Штейнера подтверждена экспериментально.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Физический смысл момента инерции тела относительно оси враще-

ния.

2.Методы вычисления момента инерции твердого тела. Вычислить момент инерции диска (цилиндра) относительно его продольной геометрической оси.

3.Какие физические законы применяются при выводе рабочей формулы для определения момента инерции? Объяснить возможность их применения.

4.Доказать теорему Гюйгенса-Штейнера. Как проверить ее экспериментально?

5.Объяснить формулы для вычисления погрешностей косвенных измерений.

ЛИТЕРАТУРА

1.Сивухин Д.В. Общий курс физики / Д.В. Сивухин. – М. : Физмат-

лит, 2005. – Т. 1. – 559 с.

2.Савельев И.В. Курс физики / И.В. Савельев. – СПб. : Лань, 2004. –

Т. 1. – 432 с.

3.Стрелков С.П. Общий курс физики. Механика / С.П. Стрелков. –

М. : Наука, 1975. – 560 с.

4.Матвеев А.Н. Механика и теория относительности / А.Н. Матвеев. – М. : Мир и образование, 2003. – 432 с.

5.Айзерман М.А. Классическая механика / М.А. Айзерман. – М. :

Наука, 1980. – С. 168–173.

6.Каленков С.Г. Практикум по физике. Механика : учеб. пособие /

С.Г. Каленков, Г.И. Соломахо. – М., 1990. – С. 95–102.

7.Физический практикум. Механика и молекулярная физика / под ред. В.И. Ивероновой. – М. : 1967. – 352 с.

ЛАБОРАТОРНАЯ РАБОТА М-4.2

ИЗУЧЕНИЕ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА НА МАЯТНИКЕ ОБЕРБЕКА

Цель работы: экспериментальная проверка основного уравнения динамики вращательного движений твердого тела.

9

ВВЕДЕНИЕ

Совокупностью поступательного и вращательного движений можно описать любое сложное движение твердого тела.

При поступательном движении все точки твердого тела движутся с одинаковыми скоростями и ускорениями. В каждом теле существует такая точка, что при описании движения всю массу тела m можно считать сосредоточенной в этой точке, а все внешние силы – приложенными к ней. Дан-

ная точка называется центром масс или центром инерции.

Поступательное движение твердого тела обычно рассматривается как движение материальной точки массой m, находящейся в центре инерции.

Вращательное движение твердого тела можно рассматривать как вращение в системе координат, начало которой совпадает с центром инерции.

Одной из основных характеристик движения является момент импульса. Рассмотрим движение частицы, положение которой характеризует-

ся радиусом-вектором r относительно произвольной точки О выбранной системы отсчета в некоторый момент времени (рис. 1). Импульс частицы в данный момент времени p m v .

Рис. 1. Момент импульса частицы относительно точки

где l = r·sinα – плечо вектора p относительно точки О.

10