
Математическая логика и теория алгоритмов (90
..pdf
A |
B |
A B |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
13.Таблица истинности дизъюнкции.
A |
B |
A B |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
14.Таблица истинности импликации.
A |
B |
A B |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
15.Таблица истинности эквиваленции.
A |
B |
A B |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
16.Формула называется тавтологией, если она принимает только истинное значение при любых значениях букв.
17.Формула называется противоречием, если она принимает только ложное значение при любых значениях букв.
18.Коммутативность конъюнкции.
A B B A. 19.Коммутативность дизъюнкции.
A B B A. 20.Ассоциативность конъюнкции.
A 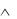 B C
B C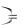 A B
A B C .
C .
21.Ассоциативность дизъюнкции.
A 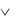 B C
B C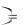 A B
A B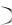 C .
C .
22.Закон исключения третьего.
A 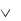 A 1.
A 1.
23.Закон противоречия.
A A 0 .
31

24.Дистрибутивность конъюнкции.
A |
B C |
A B |
A |
C . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
25.Дистрибутивность дизъюнкции. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
A |
B C |
A B |
A |
C . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
26.Тавтологии - A 1 |
1, |
A |
0 |
A . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
27.Тавтологии - A 1 |
A , |
A |
0 |
0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
28.При доказательстве, что формула A |
B |
A является тавтологией, |
|
|
|
|
||||||||||||||||
предполагаем, что в некоторой интерпретации |
|
A |
B |
A |
|
0 . |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|||||||||||||||||
29.При доказательстве, что формула A |
B |
C |
A |
B |
C |
является |
|
|
|
|
||||||||||||
тавтологией, предполагаем, что в некоторой интерпретации |
|
|
|
A B |
C |
|
1. |
|||||||||||||||
|
|
|
|
|||||||||||||||||||
30.При доказательстве, что формула A |
B |
C |
A |
B |
C |
является |
|
|
|
|
||||||||||||
тавтологией, предполагаем, что в некоторой интерпретации |
|
A B |
C |
|
|
0 . |
||||||||||||||||
|
|
|
||||||||||||||||||||
31.Пусть формулы A |
и A |
B – тавтологии. Тогда тавтологией является |
|
|
||||||||||||||||||
формула B . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
32.Пусть формула A – тавтология, P , |
P , …, P |
– буквы в формуле A ; |
A |
, |
||||||||||||||||||
|
|
|
|
|
|
1 |
2 |
k |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
A2 , …, Ak – |
любые формулы. Тогда тавтологией является формула |
|
|
|
|
|||||||||||||||||
BA A1, A2 ,..., Ak .
33.Формулы A и B называются логически эквивалентными тогда и только
тогда, когда формула A B – тавтология.
34.Отношение логической эквивалентности является отношением
эквивалентности. |
|
|
|
|
|
|
|
35.Формула A |
B C |
логически эквивалентна формуле |
A |
B |
A C . |
||
36.Формула |
A логически эквивалентна формуле A . |
|
|
|
|||
37.Формула A |
B логически эквивалентна формуле |
A |
B . |
|
|
||
38.Формула A логически влечет формулу B , если формула A |
B – тавтология. |
||||||
39.Отношение предпорядка рефлексивно и транзитивно. |
|
|
|
||||
40.Отношение логического следствия является отношением предпорядка. |
|||||||
41.Формула A логически влечет формулу |
A. |
|
|
|
|
||
42.Формула A логически влечет формулу A . |
|
|
|
|
|
||
43.Формула A логически влечет формулу B |
A . |
|
|
|
|
||
44.Формула A |
B |
C логически влечет формулу |
A |
B |
A |
C . |
|
45.Формула A |
B логически влечет формулу B |
A. |
|
|
|
||
46.К символам алфавита в исчислении высказываний не относятся |
, . |
||
47.К символам алфавита в исчислении высказываний не относятся |
, . |
||
48.Формулой исчисления высказываний является символ |
A . |
|
|
49.Формулой исчисления высказываний является символ A . |
|
|
|
50.Формулой исчисления высказываний является символ A |
B |
C . |
|
51.Формулой исчисления высказываний является символ |
A |
B |
A . |
52.Правило вывода MP имеет вид A, A B ├ B . |
|
|
|
53.Аксиомой исчисления высказываний является A B |
A . |
|
|
32

54.Аксиомой исчисления высказываний является
A |
B |
|
C |
A |
B |
A |
C . |
|
|
|
|
|
|
55.Аксиомой исчисления высказываний является |
B |
A |
B A |
B . |
|||||||||
56.Аксиома А1 с подстановкой вместо B |
B имеет вид A |
B |
A . |
|
|||||||||
57.Аксиома А2 с подстановкой вместо A A C имеет вид |
|
|
|||||||||||
A C |
|
B C |
|
A C B |
A C C . |
|
|
|
|
||||
58.Аксиома А3 с подстановкой вместо B |
B имеет вид |
|
|
|
|||||||||
|
B |
A |
B |
A |
|
B . |
|
|
|
|
|
|
|
59. |
– множество формул, |
A , |
B – формулы. Тогда теорема дедукции |
, |
|||||||||
A ├ B |
|
├ A |
B . |
|
|
|
|
|
|
|
|
|
|
60. |
– множество формул, |
A , B – формулы. Тогда теорема, обратная теореме |
|||||||||||
дедукции |
|
|
|
|
|
|
|
|
|
|
|
||
├ A |
B |
, |
A ├ B . |
|
|
|
|
|
|
|
|
||
61.Теория L полная и непротиворечивая. |
|
|
|
|
|
||||||||
62.Теория L разрешимая и непротиворечивая. |
|
|
|
|
|||||||||
63.Выводом формулы ( |
B |
A) A |
B |
в исчислении высказываний |
|
||||||||
является: |
|
|
|
|
|
|
|
|
|
|
|
||
|
По теореме, обратной теореме дедукции, |
|
|
|
|
||||||||
|
├ ( B |
|
A) |
A |
B |
равносильно |
B |
A, A ├ B . |
|
|
|||
1.B 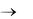 A – гипотеза.
A – гипотеза.
2.A – гипотеза.
3. |
( |
B |
A) |
B A B – аксиома А3. |
4. |
( |
B |
A) |
B . MP 1,3. |
5. |
A |
|
( B |
A) – аксиома А1 (с подстановкой вместо B – B ). |
6.B A . MP 2,5.
7.B . MP 6,3.
64.Выводом формулы |
A |
B |
C |
B A C |
в исчислении высказываний |
является: |
|
|
|
|
|
По теореме, обратной теореме дедукции, |
|
||||
├ A B C |
B |
A |
C |
равносильно A |
B C , B, A ├ C . |
1. A B C – гипотеза.
2.B – гипотеза.
3.A – гипотеза.
4.B C . MP 3,1.
5.C . MP 2,4.
65.Выводом формулы A |
B |
C |
B |
A |
C B B в исчислении |
|
высказываний является: |
|
|
|
|
||
По теореме, обратной теореме дедукции, |
|
├ |
||||
A B |
C B |
A |
C B |
B |
равносильно |
|
A B, C B A,C B ├ B .
33

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»
1. |
A |
B – |
гипотеза. |
2. |
C |
B |
A – гипотеза. |
3.C B – гипотеза.
4.A . MP 3,2.
5.B . MP 4,1.
66. n -местным предикатом на множестве X называется n -местная функция
|
f : X n |
0,1 . |
|
67. |
xi A |
xi |
A . |
68. |
xi A |
xi |
A . |
69. |
xi A |
xi |
A . |
70. |
xi A |
xi |
A . |
71.Предикат |
xi A(x1, x2 ,..., xn ) является n |
1 -местным. |
|||||
72.Предикат |
xi A(x1, x2 ,..., xn ) |
является n |
1 -местным. |
||||
73.Местность предиката |
x |
2 |
0 на множестве R равна 1. |
||||
74.Местность предиката |
x x3 |
8 |
0 на множестве R равна 0. |
||||
75.Местность предиката x |
y |
1 на множестве R равна 2. |
|||||
76.Местность предиката |
x |
x |
y2 |
0 на множестве R равна 1. |
|||
77.Среди данных предикатов на множестве R высказываниями являются |
|||||||
x x |
5 и “Все трехзначные натуральные числа простые”. |
||||||
78.Среди данных предикатов на множестве R высказываниями являются |
|||||||
x x |
5 и |
x x2 0 . |
|
|
|
|
|
79.Среди данных предикатов на множестве R высказываниями являются “Если сумма цифр натурального числа делится нацело на 3, то число делится на 3”
и x sin2 x cos2 x |
1 . |
|
|
|
|
|
|
80.Среди данных предикатов на множестве R высказываниями являются |
|||||||
ln x 0 и x |
sin2 x |
1 . |
|
|
|
|
|
81.Пусть A(x1, x2 ,..., xn ) – |
n -местный предикат, xi |
– переменная в предикате. |
|||||
Тогда предикат |
xi A(x1, x2 ,..., xn ) A( x1 , x2 ,..., xn ) |
1. |
|
||||
82.Пусть A(x1, x2 ,..., xn ) – |
n -местный предикат, xi |
– переменная в предикате. |
|||||
Тогда предикат |
A(x1, x2 ,..., xn ) |
xi A( x1 , x2 ,..., xn ) |
1. |
||||
83.Справедливо соотношение |
x P(x) |
C |
xP(x) |
C . |
|
||
84.Справедливо соотношение |
x P(x) |
C |
xP(x) |
C . |
|
||
85.Справедливо соотношение |
x P(x) |
C |
xP(x) |
C . |
|
||
86.Справедливо соотношение |
x P(x) |
C |
xP(x) |
C . |
|
||
87.Справедливо соотношение |
x P(x) |
Q(x) |
xP(x) |
xQ(x) . |
|||
88.Справедливо соотношение |
x P(x) |
Q(x) |
xP(x) |
xQ(x) . |
|||
89.Имеет место соотношение |
x yP(x, y) |
y xP(x, y) ... |
|
90.Имеет место соотношение |
x |
yP(x, y) |
y xP(x, y) . |
91.Имеет место соотношение |
x |
yP(x, y) |
y xP(x, y) . |
34

92.Имеет место соотношение y xP(x, y) x yP(x, y) . 93.Предикатная формула находится в приведенной форме, если в ней
использованы только кванторные операции, а также операции инверсии, конъюнкции, дизъюнкции, причем инверсия относится только к предикатным буквам.
94.Предикатная формула находится в предваренной нормальной форме, если она имеет вид Q1x1Q2 x2 ...Qk xk A , где Q1, Q2 ,..., Qk - кванторы всеобщности или
существования, а формула A находится в приведенной форме и не содержит кванторов.
95.Формулы, при приведении которых к предваренной нормальной форме
нужно вводить новые переменные, - |
x yP(x, y) |
x yQ(x, y) , |
|
x yP(x, y) |
x yQ(x, y) . |
|
|
96.Интерпретацией множества формул |
называется область интерпретации X |
||
и заданное на ней соответствие, при котором каждой предикатной букве Ak(n) ставится в соответствие n -местный предикат на множестве X , каждой функциональной букве fk(n) ставится в соответствие n -местная функция на множестве X , каждой предметной константе ai ставится в соответствие
элемент множества X .
97.Формула теории первого порядка называется логически общезначимой, если
она истинна в любой интерпретации. |
|
|
|
|
|
|
|
|
98.Формула теории первого порядка называется противоречивой, если она |
|
|||||||
ложна в любой интерпретации. |
|
|
|
|
|
|
|
|
99.Формулой исчисления предикатов является символ |
x A(2) f (1) |
x |
, f (2) |
x , x . |
||||
|
|
1 |
1 |
1 |
1 |
2 |
1 |
2 |
100. Аксиомой исчисления предикатов является |
xi A(xi ) |
|
A(t) , где терм t |
|
||||
свободен для переменной xi в формуле A(xi ) . |
|
|
|
|
|
|
|
|
101. Аксиомой исчисления предикатов является |
xi A |
B |
A |
|
xi B , где xi |
|||
– несвободная переменная в формуле A .
102.Правило обобщения A ├ xA.
103.Чистое исчисление предикатов (исчисление предикатов без собственных аксиом) - полная и непротиворечивая теория.
104.Чистое исчисление предикатов (исчисление предикатов без собственных аксиом) – в общем случае неразрешимая и непротиворечивая теория.
105.Теория первого порядка с собственными аксиомами - неразрешимая и неполная теория.
106. |
Предложение – это дизъюнкция формул вида A или A, где A – атом |
||||
(буква). |
|
|
|
|
|
107. |
При преобразовании формулы к множеству предложений импликация |
||||
заменяется по формуле A |
B |
A B . |
|
|
|
108. |
При преобразовании формулы к множеству предложений двойная |
||||
инверсия заменяется по формуле |
A |
A. |
|
||
109. |
При преобразовании формулы к множеству предложений используются |
||||
законы де Моргана A B |
A |
B , |
A B |
A B . |
|
35

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»
110. |
При преобразовании формулы к множеству предложений используются |
||||||||
дистрибутивные законы A |
B |
C |
A |
B |
A |
C , |
|
||
A |
B C |
A B A C . |
|
|
|
|
|
|
|
111. |
При преобразовании формулы к множеству предложений используются |
||||||||
законы идемпотентности A |
A |
A, |
A |
A |
A. |
|
|
||
112. |
Если |
, A├ F , где F – тождественно ложная формула, то |
├ A . |
||||||
113. |
Если из формулы A получено множество предложений, то формула A |
||||||||
тождественно ложна тогда и только тогда, когда множество |
невыполнимо. |
||||||||
114. |
Правило резолюций имеет вид С1 |
P |
C1 , С2 |
P C2 . С1 , С2 ├ C1 C2 . |
|||||
115.Истинным утверждением является - резольвента логически следует из резольвируемых предложений.
116.Истинным утверждением является - резольвента логически следует из резольвируемых предложений.
117. |
Если методом резолюций доказывается выводимость |
├ A , где – |
множество формул, то к множеству предложений преобразуются A и все |
||
формулы из . |
|
|
118. |
Если методом резолюций доказывается выводимость |
├ A , то к |
множеству предложений преобразуется формула A . |
|
|
119. |
Если методом резолюций доказывается выводимость |
├ A , то к |
множеству предложений преобразуется формула A . |
|
|
120.При доказательстве выводимости 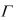 ├ A методом резолюций резольвенты добавляются во множество предложений до тех пор, пока не будет получено пустое предложение.
├ A методом резолюций резольвенты добавляются во множество предложений до тех пор, пока не будет получено пустое предложение.
121.При доказательстве выводимости  ├ A методом резолюций, если среди множества предложений нет резольвируемых предложений, теорема опровергнута, и формула A не выводима из множества формул
├ A методом резолюций, если среди множества предложений нет резольвируемых предложений, теорема опровергнута, и формула A не выводима из множества формул 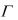 .
.
122.При доказательстве выводимости 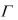 ├ A методом резолюций, если получено пустое предложение, теорема доказана. Имеет место выводимость
├ A методом резолюций, если получено пустое предложение, теорема доказана. Имеет место выводимость
|
├ A . |
|
|
|
|
|
123. |
Резольвируемые предложения A , |
A и A |
B , A |
B . |
|
|
124. |
Резольвируемые предложения A |
C , |
A C и C |
B , |
B . |
|
125. |
Резольвируемые предложения C |
B , |
B и |
A |
B , A |
B . |
126.Состония управляющего устройства машины Тьюринга q0 , q1 , …, qn .
127.Состояния управляющего устройства машины Тьюринга обозначаются буквами внутреннего алфавита Q 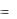 q0 , q1, , qm .
q0 , q1, , qm .
128.Лента машины Тьюринга предполагается потенциально бесконечной в обе стороны.
129.Символы на ленте машины Тьюринга обозначаются буквами внешнего алфавита A 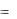 a0 , a1, , an .
a0 , a1, , an .
130.Во внешнем алфавите a0 , a1 , …, an для машины Тьюринга пустой символ обозначается a0 .
131.Число ячеек, которые обозревает считываюшая и пишущая головка машины Тьюринга в каждый тактовый момент времени, равно 1.
36

132.В зависимости от состояния управляющего устройства машины Тьюринга считываюшая и пишущая головка в каждый тактовый момент времени остается на месте либо передвигается на одну ячейку вправо или влево.
133.В зависимости от состояния управляющего устройства машины Тьюринга считываюшая и пишущая головка в каждый тактовый момент времени оставляет обозреваемый символ без изменения или записывает на место обозреваемого символа любой другой символ внешнего алфавита (либо стирает обозреваемый символ).
134.qia j qijaij Dij – общий вид команды для машины Тьюринга. Тогда текущее
состояние управляющего устройства - qi .
135.qia j qijaij Dij – общий вид команды для машины Тьюринга. Тогда новое
состояние управляющего устройства - qij .
136.qia j qijaij Dij – общий вид команды для машины Тьюринга. Тогда
обозреваемый символ - a j .
137.qia j qijaij Dij – общий вид команды для машины Тьюринга. Тогда новый
символ - aij .
138.qia j qijaij Dij – общий вид команды для машины Тьюринга. Тогда символ
сдвига - Dij .
139. В программе для машины Тьюринга начальное состояние обозначается
q1 .
140.В программе для машины Тьюринга заключительное состояние обозначается q0 .
141.В программе для машины Тьюринга сдвиг вправо обозначается R .
142.В программе для машины Тьюринга сдвиг влево обозначается L .
143.В программе для машины Тьюринга операция “на месте” обозначается E .
144.Пустой символ в алфавите E 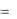 0,1 в машине Тьюринга обозначается 0.
0,1 в машине Тьюринга обозначается 0.
145.Индекс в обозначении начального состояния машины Тьюринга q... равен
1.
146. Индекс в обозначении заключительного состояния машины Тьюринга q...
равен 0.
147. Пусть qi – текущее состояние управляющего устройства, a j – обозреваемый символ, qij – новое состояние управляющего устройства, aij
– новый символ, Dij , R , L , E – символы сдвига. Общий вид команды для
машины Тьюринга qia j qijaij Dij .
148. Наибольшее допустимое число команд в программе для машины Тьюринга, соответствующее состоянию управляющего устройства qi при
данном i равно 2.
149. Число символов сдвига для машины Тьюринга равно 3.
37

150. Если вид ленты машины Тьюринга в данный момент времени определен конфигурацией вида a j1 a j l 1 qia j l a j s , то головкой в данный момент
обозревается символ a j l .
151.Любой символ на ленте, не записанный в конфигурации машины Тьюринга в алфавите E 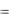 0,1 - 0.
0,1 - 0.
152.Если вид ленты машины Тьюринга в данный момент времени определен конфигурацией вида a j1 a j l 1 qia j l a j s , то в данный момент времени на
ленте записано слово a j1 a jl 1 a jl a j s .
153.Записанные подряд в конфигурации для машины Тьюринга n единиц обозначаются 1n .
154.Записанные подряд в конфигурации для машины Тьюринга m нулей
обозначаются 0m .
155.Машина Тьюринга T применима к слову P , если, начав работу на некотором слове P , машина останавливается через некоторое число шагов.
156.Машина Тьюринга T не применима к слову P , если, начав работу на некотором слове P , машина никогда не останавливается, либо, начав работу на некотором слове P , машина бесконечно повторяет одни и те же конфигурации.
157.Машина Тьюринга может не обладать свойствами: “В программе обязательно есть символ q0 ” и “Каждому состоянию управляющего
устройства обязательно соответствует две команды”.
158. Машина Тьюринга может не обладать свойствами “В программе число команд, начинающихся с q1 , может быть больше двух” и “Символ E
означает окончание работы программы”.
159. Текущее состояние управляющего устройства - qi . Обозреваемый символ - a j . Новое состояние управляющего устройства - qij . Новый символ - aij . Символ сдвига - Dij .
160. Начальное состояние управляющего устройства - q1 . Заключительное состояние управляющего устройства - q0 . Сдвиг вправо - R . Сдвиг влево - L .
Операция “на месте” - E .
161. Начальное состояние управляющего устройства - q1 . Заключительное состояние управляющего устройства - q0 . Обозреваемый символ - a j . Новый символ - aij . Сдвиг вправо - R .
162. Команда для машины Тьюринга имеет вид q1 0q2 1R . Текущее состояние управляющего устройства - q1 . Новое состояние управляющего устройства - q2 . Символ сдвига - R . Обозреваемый символ внешнего алфавита - 0. Новый символ внешнего алфавита - 1.
38

163. Команда для машины Тьюринга имеет вид q21q3 0R . Текущее состояние управляющего устройства - q2 . Новое состояние управляющего устройства - q3 . Символ сдвига - R . Обозреваемый символ внешнего алфавита - 1. Новый
символ внешнего алфавита - 0.
164. Команда для машины Тьюринга имеет вид q11q0 0L . Текущее состояние управляющего устройства - q1 . Новое состояние управляющего устройства - q0 . Символ сдвига - L . Обозреваемый символ внешнего алфавита - 1. Новый
символ внешнего алфавита - 0.
165. Команда для машины Тьюринга имеет вид q3 0q01L . Текущее состояние управляющего устройства - q3 . Новое состояние управляющего устройства - q0 . Символ сдвига - L . Обозреваемый символ внешнего алфавита - 0. Новый
символ внешнего алфавита - 1.
166. Команда для машины Тьюринга имеет вид q2 0q11E . Текущее состояние управляющего устройства - q2 . Новое состояние управляющего устройства - q1 . Символ сдвига - E . Обозреваемый символ внешнего алфавита - 0. Новый символ внешнего алфавита - 1.
167.Тезис Тьюринга - всякий алгоритм может быть реализован соответствующей машиной Тьюринга.
168.Пусть Т – произвольная программа (машина Тьюринга). Двойственная Т программа – это программа Т*, которая получается из Т заменой (во всех командах) R на L и наоборот.
169.Пусть в начальный момент времени имеется конфигурация ...qia1a2... , и
машина Тьюринга Т в момент времени t переработает ее в конфигурацию
...c1c2...qics ... . Тогда двойственная машина Т* конфигурацию ...a2qia1... в момент времени t переработает в конфигурацию ...qics ...c2c1... .
|
q1 0q2 0L |
|
170. Двойственная машина для машины Тьюринга T : |
q11q1 0R |
имеет вид |
q2 0q21L |
||
|
q21q0 0R |
|
q1 0q2 0R
T: q11q1 0L . q2 0q2 1R
|
q2 1q0 0L |
|
171. |
Примитивно-рекурсивные функции определены на множестве N 0 . |
|
172. |
Примитивно-рекурсивная функция n переменных f n : N0n N0 . |
|
173. |
, 174. |
Простейшей примитивно-рекурсивной функцией является |
s(x) x |
1 . |
|
175. |
, 177. |
Простейшей примитивно-рекурсивной функцией является 0(x) 0 . |
39

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»
176. |
, 178. Простейшей примитивно-рекурсивной функцией является |
|
||||||||||||||||||||||||||||||||||||||
I n (x , x ,...,x ,...,x ) |
x , 1 |
i |
|
n . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
i |
1 2 |
|
i |
n |
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
179. |
Пусть f n (x , x |
2 |
,...,x |
n |
) |
, g m |
(t ,t |
2 |
,...,t |
m |
) , g m (t ,t |
2 |
,...,t |
m |
) , …, |
g m (t ,t |
2 |
,...,t |
m |
) – |
||||||||||||||||||||
|
|
|
1 |
|
|
1 1 |
|
|
|
|
|
|
|
2 1 |
|
|
|
|
|
|
|
|
n 1 |
|
|
|||||||||||||||
примитивно-рекурсивные функции. C помощью оператора суперпозиции из |
||||||||||||||||||||||||||||||||||||||||
этих функций получена функция |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
F m (gm , g m ,..., g m ) |
|
|
f n (gm (t , t |
,..., t |
m |
), g m |
(t , t |
,..., t |
m |
),..., g m (t , t |
,..., t |
m |
)) . |
|
|
|
|
|||||||||||||||||||||||
n |
1 |
2 |
n |
|
|
|
1 |
|
1 2 |
|
|
|
2 |
|
1 2 |
|
|
|
|
|
|
|
n 1 2 |
|
|
|
|
|
|
|
||||||||||
180. |
Суперпозицией s |
0 |
x |
является функция f (x) |
|
1. |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
181. |
Суперпозицией 0 s |
x |
является функция f (x) |
|
0 . |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
182. |
Суперпозицией s |
s |
|
x |
является функция f (x) |
|
x |
2 . |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
183. |
Суперпозицией s |
s |
|
s x |
|
является функция f (x) |
x |
|
3 . |
|
|
|
|
|||||||||||||||||||||||||||
184. |
Суперпозицией s |
I |
2 |
x, y |
является функция f (x, y) |
x |
|
1. |
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
185. |
Суперпозицией 0 |
I |
2 |
x, y |
является функция f (x, y) |
0 . |
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
186. |
Пусть |
n (x , x |
2 |
,...,x |
n |
) |
и |
|
n 2 (x , x |
2 |
,...,x |
n |
, y, z) – примитивно-рекурсивные |
|||||||||||||||||||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
функции. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
C помощью оператора примитивной рекурсии f n 1 |
R ( |
|
|
n , n |
2 ) из этих |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
функций получена функция f n 1 (x , x |
,...,x |
n |
, y) |
по следующей схеме |
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
f n 1(x , x ,...,x ,0) |
|
n (x , x ,...,x ) , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
1 |
2 |
n |
|
|
|
|
1 |
2 |
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f n 1(x , x ,...,x , y |
|
1) |
|
n |
2 (x , x ,..., x , y, f n 1 (x x ,..., x , y)) . |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
1 |
2 |
n |
|
|
|
|
|
1 |
2 |
|
|
|
n |
|
|
|
|
|
|
|
1, 2 |
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
||||
187. |
Оператор примитивной рекурсии f n 1 |
|
|
R ( |
n , |
|
n |
2 ) . |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
188. |
- 191. Схема примитивной рекурсии (при n |
0) - |
f (0) |
|
a |
g( y, f ( y)) . |
||||||||||||||||||||||||||||||||||
f ( y |
|
|
1) |
|||||||||||||||||||||||||||||||||||||
192.Примитивно-рекурсивной функцией называется числовая функция, получаемая за конечное число шагов из простейших примитивнорекурсивных функций с помощью операторов суперпозиции и примитивной рекурсии.
193.Первые три шага построения функции f (x, y) по схеме примитивной
рекурсии |
f |
x, 0 |
x , f x,1 |
x2 , f x, 2 |
x3 . Функция f (x, y) |
x y |
1 . |
|
194. Первые три шага построения функции |
f (x, y) по схеме примитивной |
|||||||
рекурсии |
f |
x, 0 |
x , f x,1 |
2x , f x, 2 |
3x . Функция f (x, y) |
x |
y 1 . |
|
195. Первые три шага построения функции |
f (x, y) по схеме примитивной |
|||||||
рекурсии f |
x, 0 |
1, f x,1 |
x , f x, 2 |
x2 . Функция f (x, y) |
x y . |
|
||
196.Частично-рекурсивной функцией называется числовая функция, получаемая за конечное число шагов из простейших примитивнорекурсивных функций с помощью операторов суперпозиции, примитивной рекурсии и минимизации.
197.Числовая функция называется общерекурсивной, если она частичнорекурсивна и всюду определена.
198.Функция f x1, x2 ,..., xn  называется эффективно вычислимой, если
называется эффективно вычислимой, если
существует алгоритм, позволяющий вычислить ее значения.
40
