
Выбор оптимального режима раскрытия складного крыла ракеты (160
..pdfМосковский государственный технический университет имени Н.Э. Баумана
С.В. Аринчев, А.В. Беляев, С.Н. Дмитриев
ВЫБОР ОПТИМАЛЬНОГО РЕЖИМА РАСКРЫТИЯ СКЛАДНОГО КРЫЛА РАКЕТЫ
Методические указания к выполнению домашнего задания
по курсу «Интегрирование уравнений динамики элементов конструкций летательных аппаратов»
М о с к в а
Издательство МГТУ им. Н.Э. Баумана
2 0 0 9
УДК 629.7.01 ББК 39.56
А81
Р е ц е н з е н т ы :
О.В. Кузнецов, С.Э. Зайцев
Аринчев С.В., Беляев А.В., Дмитриев С.Н.
А81 Выбор оптимального режима раскрытия складного крыла ракеты: Метод. указания к выполнению домашнего задания по курсу «Интегрирование уравнений динамики элементов конструкций летательных аппаратов». — М.: Изд-во МГТУ им. Н.Э. Баумана, 2009. — 16 с.: ил.
Предложена расчетная модель складного крыла, имеющего две линии складывания. Результирующие уравнения динамики приведены к форме Коши. Они используются для решения задачи оптимизации, в которой находится минимальное время раскрытия крыла при учете ограничения по уровню перегрузки фюзеляжа. Рассмотрен пример анимации результатов расчета.
Для студентов 5-го курса, изучающих дисциплину «Динамика конструкций аэрокосмических систем и крылатых ракет».
УДК 629.7.01 ББК 39.56
© МГТУ им. Н.Э. Баумана, 2009
ПРЕДИСЛОВИЕ
В методических указаниях рассматривается задача оптимизации режима раскрытия складного крыла ракеты. Для ее решения на координатной плоскости значений сил поршня агрегата раскрытия крыла (АРК) и жесткости приводного упругого элемента концевой панели необходимо отыскать точку, в которой достигается минимум времени раскрытия крыла при условии, что перегрузка фюзеляжа не превышает нормативного значения. Процедура минимизации сводится к сканированию узлов сетки значений параметров в заданной прямоугольной области на координатной плоскости. В каждой точке поиска для указанных начальных условий интегрируются уравнения динамики раскрытия складного крыла. Оптимальный режим выбирают с учетом положения линий уровня целевой функции и функции ограничений.
Для решения поставленной задачи при выполнении домашнего задания студентам обеспечивается компьютерная поддержка.
1. ОСНОВНЫЕ ДОПУЩЕНИЯ РАСЧЕТА
Складывание крыла ракеты обеспечивает существенное уменьшение габаритных размеров изделия и компактное размещение его на носителе. Крыло ракеты раскрывается уже после старта. С одной стороны, чем быстрее возникнет подъемная сила, тем лучше. С другой стороны, быстрое раскрытие крыла большого размаха может привести к возникновению существенных перегрузок фюзеляжа. На практике эти перегрузки ограничивают в соответствии с требованиями отраслевых нормативов.
Динамика раскрытия крыла зависит от способа его складывания. Рассматриваемый в методических указаниях способ складывания представлен на рис. 1.
3

|
|
1 |
|
α |
|
Oф |
|
2 |
Oк |
O1 |
|
|
|
3 |
|
|
4 |
|
|
5 |
|
O2 |
6 |
|
|
7 |
Рис. 1. Пример складывания крыла в контейнере (вид с носика изделия):
1 — фюзеляж; 2 — концевая панель; 3 — первая линия складывания, идущая вдоль бортовой хорды; 4 — корневая панель крыла; 5 — щель для слива пограничного слоя; 6 — вторая линия складывания, разделяющая крыло на корневую и концевую панели; 7 — входное отверстие плоского воздухозаборника
Фюзеляж и крылья будем считать абсолютно жесткими телами, соединенными упругими связями. Правое и левое крылья ракеты раскрываются синхронно. При раскрытии крыла ракета совершает плоскопараллельное движение. Таким образом, состояние ракеты можно описать тремя фазовыми координатами y0, ϕ1, ϕ2: вертикальное смещение фюзеляжа, угол поворота корневой панели и угол поворота концевой панели соответственно (рис. 2). Упрощение расчетной модели раскрытия крыла оправдывается необходимостью многократного интегрирования уравнений динамики при оптимизации параметров системы в процессе выполнения студентом домашнего задания.
Раскрытие корневой панели крыла обеспечивается работой агрегата раскрытия крыла, который поворачивает ее в рабочее положение. Принято, что сила толкания F с течением времени остается постоянной. Сила F является первым варьируемым параметром в рассматриваемой задаче оптимизации. Линия действия силы тол-
4

кания АВ и начальное плечо толкания lF показаны на рис. 3. С течением времени линия действия поворачивается на угол θ. Фазовая координата ϕ1 и угол θ связаны между собой. Раскрытие концевой панели крыла обеспечивается приводным упругим элементом с жесткостью k2, создающим упругий момент k2(ϕ2 – ϕ1). Коэффициент жесткости приводного упругого элемента k2 является вторым варьируемым параметром в рассматриваемой задаче оптимизации. Значения указанных двух варьируемых параметров оптимизации изображают точками на координатной плоскости.
y
O2 ϕ2
y0
ϕ1
O1
O
x
Рис. 2. Основные фазовые координаты задачи
y
|
|
F |
|
|
A |
|
|
lF |
|
O1 |
ϕ1 |
|
|
|
|
lF |
θ |
|
|
|
|
|
B |
О |
|
x |
Рис. 3. Линия действия силы толкания корневой панели крыла
5
При разработке программы интегрирования уравнений динамики необходимо задаться логикой раскрытия панелей. В момент времени, когда корневая панель первый раз оказывается в горизонтальной плоскости, сила толкания обнуляется. Агрегат раскрытия крыла отстыковывается и сбрасывается. В этот же момент корневая панель фиксируется с помощью замка. Фактически это означает, что в окрестности бортовой хорды включается в работу угловой упругий элемент, создающий упругий момент k1ϕ1. Здесь также включается в работу угловой демпфер, создающий демпфирующий момент вязкого трения γ1ϕ1.
То же самое происходит с концевой панелью. Положение концевой панели фиксируется относительно корневой. Когда концевая панель первый раз попадает в одну плоскость с корневой панелью, концевая панель фиксируется с помощью замка. Механический момент замка моделируется путем увеличения параметра k2 на порядок. При раскрытии крыла в работу включается также угловой демпфер, создающий демпфирующий момент вязкого трения γ2 (ϕ2 − ϕ1).
При выполнении расчетов аэродинамические нагрузки не учитываются. Стартовая разгонная ступень отсутствует. Ракета совершает свободное падение с самолета-носителя. Начальное ускорение фюзеляжа ракеты равно ускорению свободного падения. При раскрытии крыла на фюзеляже возникают перегрузки, имеющие колебательный характер. После затухания колебаний изделие продолжает падать с ускорением свободного падения.
2. УРАВНЕНИЯ ДИНАМИКИ РАСКРЫТИЯ СКЛАДНОГО КРЫЛА
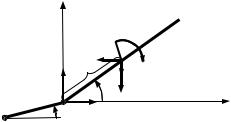
На концевую панель крыла действуют реакции в шарнире О2 на линии складывания, сила инерции, сила тяжести, момент приводного упругого элемента (замка фиксации концевой панели относительно корневой) и демпфирующий момент замка фиксации концевой панели (рис. 4). Уравнения квазистатического равновесия концевой панели для сил в проекциях на оси координат и для моментов относительно центра масс панели имеют вид
6
Y2 − m2 g − m2 y = 0;
X 2 − m2 x = 0;
−J2ϕ2 − k2 (ϕ2 − ϕ1) − γ2 (ϕ2 − ϕ1) +
+X2lц.м2 sin ϕ2 −Y2lц.м2 cos ϕ2 = 0,
где lц.м2 — расстояние от линии складывания крыла до центра масс концевой панели.
y
|
|
|
|
|
|
|
|
|
|
|
m x |
2 |
M = k2 (ϕ2 − ϕ1) + γ |
||
|
|
|
2 |
2 (ϕ2 |
− ϕ1) |
||
Y2 |
lц.м2 |
|
|
|
|
||
|
|
|
|
|
m2 y2 |
|
|
|
O |
|
ϕ2 |
m g |
|
|
|
2 |
|
|
2 |
|
|
||
O1
|
|
x |
|
ϕ1 X |
|||
2 |
|||
Рис. 4. Силы, действующие на концевую панель крыла
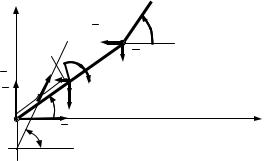
Силы, действующие на корневую панель крыла, показаны на рис. 5. Это реакции в шарнирах О1 и О2, сила инерции, сила тяжести, момент приводного упругого элемента концевой панели (замка фиксации концевой панели относительно корневой), демпфирующий момент замка фиксации концевой панели, момент замка фиксации корневой панели, демпфирующий момент замка фиксации корневой панели и сила толкания, действующая со стороны агрегата раскрытия крыла. Уравнения квазистатического равновесия корневой панели для сил в проекциях на оси координат и для моментов относительно центра масс панели имеют вид
Y1 − Y2 − m1g − m1 y1 + F sin θ = 0;
X1 − X2 − m1x1 + F cos θ = 0;
−J1ϕ1 − k1ϕ1 − γ1ϕ1 + k2 (ϕ2 − ϕ1) + γ2 (ϕ2 − ϕ1) −
−F sin(θ − ϕ1)(lц.м1 − lF ) − Y1lц.м1 cos ϕ1 + X1lц.м1 sin ϕ1 −
−Y2 (l1 − lц.м1) cos ϕ1 + X2 (l1 − lц.м1) sin ϕ1 = 0,
7
где l1 — длина корневой панели; lц.м1 — расстояние от бортовой хорды до центра масс корневой панели.
y |
|
ϕ2 |
|
|
|
|
|
|
|
|
|
|
X2 |
O2 |
|
|
|
|
|
Y |
|
|
|
m1x1 |
|
2 |
|
|
|
F |
|
|
+ k2 (ϕ1 − ϕ2 ) + γ |
|
|
M = k1ϕ1 + γ1ϕ1 |
2 (ϕ1 |
− ϕ2 ) |
|||
lц.м1 |
|
|
|
|
|
Y1 |
m1 y1 |
|
|
|
|
ϕ1 |
m g |
|
|
|
|
O1 |
1 |
|
|
|
|
θ X1 |
x |
Рис. 5. Силы, действующие на корневую панель крыла
Силы, действующие на фюзеляж и принимаемые во внимание при составлении уравнений равновесия фюзеляжа, показаны на рис. 6. Необходимо иметь в виду, что на фюзеляж действуют силы со стороны обоих крыльев, некоторые из этих сил уравновешивают друг друга. Крылья раскрываются синхронно, поэтому фюзеляж движется поступательно вдоль вертикальной оси, не вращаясь. Уравнение динамики поступательного движения имеет вид
−2Y1 − m0 g − m0 y0 − 2F sin θ = 0,
где m0 — масса фюзеляжа.
Углы поворота панелей не являются малыми, поэтому уравнения динамики раскрытия крыла геометрически нелинейны. Нелинейность данных уравнений также обусловлена принятой логической схемой раскрытия крыла.
Полученная система включает семь уравнений, а складное крыло описывается тремя фазовыми координатами. При составлении уравнений в рассмотрение введены дополнительные неизвестные: реакции опор X1, X2 , Y1, Y2 и составляющие линейных уско-
рений центров масс панелей x1, x2 , y1, y2 , чтобы исключить
дополнительные неизвестные, составляющие ускорений выражают через основные фазовые координаты. Четыре из семи уравнений
8

динамики используются для выражения реакций опор. Оставшиеся три уравнения содержат только три основные фазовые координаты задачи.
y
Oф
m0 y0
m0 g  O1
O1 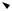
θ
Y1
F
O |
x |
|
Рис. 6. Силы, действующие на фюзеляж ракеты
Смещения центров масс панелей могут быть выражены через основные фазовые координаты задачи:
y1 = y0 + lц.м1 sin ϕ1;
x1 = lц.м1(cos ϕ1 −1);
y2 = y0 + l1 sin ϕ1 + lц.м1 sin ϕ2 ;
x2 = l1(cos ϕ1 −1) + lц.м2 (cos ϕ2 −1).
Двукратное дифференцирование данных выражений приводит к системе
|
|
|
|
|
|
|
y1 |
= ay1 + by1ϕ1 |
+ y0 ; |
|
|
|
|
|
|
|
|
|
|
|
x1 |
= ax1 + bx1ϕ1; |
|
|
|
|
|
|
|
|
|
|
|
; |
y2 |
= ay 2 + by 2ϕ1 |
+ cy 2 + d y 2ϕ2 |
+ y0 |
|||
|
|
|
|
, |
|
|
x2 |
= ax2 + bx 2ϕ1 |
|
+ cx 2 + dx 2ϕ2 |
|
|
|
|
2 |
|
|
|
|
|
где ay1 = −lц.м1 sin ϕ1 ϕ1 ; by1 = lц.м1 cos ϕ1 и т. п. |
|
|||||
9
Существенно также, что вторые производные основных фазовых координат входят в эти выражения линейно. Это позволяет записать результирующие уравнения динамики в форме Коши.
Рассмотрим теперь процедуру исключения неизвестных реакций опор из уравнений динамики. В качестве примера возьмем первое уравнение системы:
Y2 − m2 g − m2 y2 = 0.
Отсюда следует выражение для неизвестной реакции Y2:
Y2 = m2 g + m2 y2 = m2 g + m2ay 2 + m2by 2ϕ1 + m2cy 2 +
+ m2dy 2ϕ2 + m2 y0 = p1 + q1ϕ1 + g1ϕ2 ,
где p1 = m2 g + m2ay 2 + m2cy 2; q1 = m2by 2; g1 = m2dy2.
Чтобы получить выражение для неизвестной реакции X2, возьмем второе уравнение динамики системы:
X2 − m2 x2 = 0.
Отсюда следует выражение для неизвестной реакции X2:
X2 = m2 x2 = m2 ax 2 + m2bx2ϕ1 + m2cx2 + m2 dx2ϕ2 =
= p2 + q2ϕ1 + g2 ϕ2 ,
где p2 = m2ax 2 + m2cx2 ; q2 = m2bx 2 ; g2 = m2dx 2.
Аналогично из двух уравнений квазистатического равновесия корневой панели для сил можно получить выражения для реакций
Y1, X1.
Построим теперь результирующие уравнения динамики для основных фазовых координат задачи в векторной форме
|
|
|
Aϕ = R |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
или в развернутой форме: |
|
|
|
|
|
|
|
|
|
|
||
A11 |
A12 |
A13 |
y0 |
|
R1 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A22 |
A23 |
|
|
|
|
= |
|
|
(1) |
|
A21 |
|
|
ϕ1 |
|
R2 |
. |
||||||
|
A |
A |
A |
|
|
|
|
|
|
R |
|
|
|
|
ϕ |
2 |
|
|
|||||||
31 |
32 |
33 |
|
|
|
|
3 |
|
|
|||
10 |
|
|
|
|
|
|
|
|
|
|
|
|
