
Механика и молекулярная физика. Законы сохранения в механике (90
.pdf
3. Определить погрешность измерения скорости пули:
а) Рассчитать среднюю квадратичную погрешность среднего смещения маятника
n
∑(xi − x)2
S x |
= |
i=1 |
|
|
|
|
|
|
|
|
n(n −1) |
|
|
|
|
б) Определить суммарную погрешность (границы доверительного интервала) среднего значения смещения
x = x 2 |
+ x |
2 = t |
2 (n)S 2 |
+ t 2 |
(∞)( |
β x |
)2 |
|||||||
|
||||||||||||||
|
α |
|
|
|
|
β |
δ |
x |
δ |
3 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Здесь xα = tδ( (n)S |
|
|
- |
случайная |
погрешность измерения |
|||||||||
x |
||||||||||||||
среднего смещения, x |
β |
= t |
δ |
(∞) |
β x |
- |
систематическая погрешность |
|||||||
|
||||||||||||||
|
|
|
|
3 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
измерения смещения, tδ(3) = 4,3 и tδ (∞)= 1,96 – коэффициенты Стьюдента при доверительной вероятности δ = 0,95 для трех измерений и бесконечно большого числа, соответственно, βх = ±1 мм – систематическая погрешность отсчетного устройства смещения.
в) Вычислить относительную ошибку измерения смещения
x εx = x
21
г) Провести анализ относительных погрешностей величин,
входящих в формулу (5) и убедиться, что ошибки определения скорости пули в основном определяются погрешностями Δх измерения смещения и разбросом m значений массы пули. В этом случае оценить относительную погрешность результата косвенного измерения можно по формуле:
εV |
= DV » |
(Dm )2 + (Dx )2 |
(7) |
||||
|
|
|
|
|
|
|
|
V |
m |
x |
|
||||
|
|
||||||
д) По значению относительной погрешности вычислить
|
|
|
|
|
|
|
измерения скорости DV = εV |
|
|
|
|
абсолютную |
погрешность |
|
|
|
V |
. |
|||||
Окончательный результат записать в виде: |
|||||||||||
V |
= |
|
± DV , |
ε |
|
|
|
= DV ×100% δ = 0,95 при n=3. |
|||
V |
|
|
|||||||||
V |
|
||||||||||
0 |
|
|
|
|
|
V |
|||||
|
|
|
|
|
|
|
|
||||
Контрольные вопросы.
1.Что понимается под баллистическим маятником?
2.Какой удар считается неупругим?
3.Сформулируйте и запишите закон сохранения импульса.
4.Получите формулу (7) для относительной погрешности косвенного измерения.
22
Литература.
1.Савельев И.В. Курс общей физики, т.1. М., «Наука», 1970, с.75.
2.Яворский Б.М., Детлаф А.А. и др. Курс физики, т.1. М., «Высш. школа», 1965, с.58.
Лабораторная работа 108
ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА
ВОССТАНОВЛЕНИЯ И ВРЕМЕНИ СОУДАРЕНИЯ УПРУГИХ
ШАРОВ
Цель работы: определить коэффициент восстановления и время
соударения упругих шаров, рассчитать энергию остаточной деформации и среднюю силу удара.
Принадлежности: электромеханическая установка для центрального соударения шаров.
I. Виды ударов и их характеристики
Удар - столкновение двух или более тел, при котором
взаимодействие длится очень короткое время.
При соударении тел друг с другом они претерпевают деформации. При этом кинетическая энергия, которой обладали тела перед ударом, частично или полностью переходит в потенциальную энергию упругой деформации и в, так называемую, внутреннюю энергию тел. Увеличение внутренней энергии тел сопровождается повышением их температуры.
При этом как показывают наблюдения, относительная скорость тел
после удара не достигает своего прежнего значения. Это объясняется тем,
23

что нет идеально упругих тел и идеально гладких поверхностей. Для количественной оценки уменьшения относительной скорости шаров вводится коэффициент восстановления k:
|
|
|
|
|
|
|
k = |
|
u |
− u2 |
|
|
|
|
1 |
|
|
. |
(1) |
|
|
|
|||||
|
|
υ1 −υ2 |
|
|
|
|
Если для сталкивающихся тел k=0, то такие тела называются абсолютно неупругими, если k= 1 — абсолютно упругими. На практике для всехтел 0 < k < 1.
Однако в некоторых случаях тела можно с большой степенью точности рассматривать либо как абсолютно упругие, либо как абсолютно неупругие.
Прямая, проходящая через точку соприкосновения тел, нормальная к поверхности их соприкосновения, называется линией удара.
Удар называется центральным, если тела до удара движутся вдоль прямой, проходящей через их центры масс. Мы будем рассматривать только центральные абсолютно упругие и абсолютно неупругие удары
Существует два предельных вида удара: абсолютно упругий и абсолютно неупругий.
Абсолютно упругий удар – удар, при котором механическая энергия тел не переходит в другие, немеханические, виды энергии.
При таком ударе кинетическая энергия переходит полностью или частично в потенциальную энергию упругой деформации. Затем тела возвращаются к первоначальной форме, отталкивая друг друга. В
итоге потенциальная энергия упругой деформации снова переходит в кинетическую энергию, и тела разлетаются со скоростями, модуль и
24

направление которых определяются двумя условиями — сохранением полной энергии и сохранением полного импульса системы тел.
Рассмотрим центральный абсолютно упругий удар двух шаров.
Пусть шары с массами m1 и m2 движутся до ударения со скоростями υ1
и υ2, а после соударения со скоростями u1 и u2. На основании закона сохранения импульса можно записать:
m1υ1 + m2υ 2 = m1u1 + m2 u 2 .
На основании закона сохранения энергии имеем:
|
|
|
|
|
|
|
m υ2 |
+ |
m υ2 |
= |
m u |
2 |
|
+ |
m u |
2 |
|
|
|
|
||
|
|
|
|
|
|
|
1 1 |
2 2 |
1 1 |
|
2 2 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
2 |
2 |
2 |
|
|
2 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Переписав |
|
эти |
|
|
равенства |
|
|
в |
|
|
виде: |
||||||||||
m υ |
1 |
− m u |
1 |
= m u |
2 |
− m υ |
2 |
|
|
m υ2 |
− m u |
2 |
= m u |
2 |
− m υ2 |
|||||||
1 |
|
1 |
2 |
2 |
|
|
|
1 |
1 |
|
1 |
1 |
2 |
2 |
2 |
2 |
||||||
и поделив второе на первое, получим:
υ1 + u1 = u 2 +υ 2 или υ1 −υ 2 = u 2 − u1 .
Таким образом, при центральном абсолютно упругом ударе
относительная скорость шаров меняет свое направление на
противоположное, оставаясь неизменной по величине, т.е.
|
|
|
|
|
|
|
k = |
u |
− u2 |
|
= 1. |
коэффициент восстановления равен: |
1 |
|
|
||
|
|||||
|
|
υ1 −υ2 |
|
|
|
Абсолютно неупругий удар - потенциальной энергии деформации не возникает; кинетическая энергия тел полностью или частично превращается во внутреннюю энергию; после удара столкнувшиеся тела либо движутся с одинаковой скоростью, либо покоятся, т.е
коэффициент восстановления равен k =0.
25
При абсолютно неупругом ударе выполняется лишь закон сохранения импульса, закон же сохранения механической энергии не соблюдается: имеет место закон сохранения суммарной энергии
различных видов — механической и внутренней.
Определение коэффициента восстановления шаров
Пусть два одинаковых шара висят на нитях равной длины. Если оба шара отклонить на одинаковые углы и отпустить, то их скорости υ в момент соударения будут одинаковыми. Эту скорость можно найти из закона сохранения энергии для шара в верхнем и нижнем
положениях: mgh = |
mυ2 |
. Если шар опускается о высоты h, то его |
||
2 |
||||
|
|
|
||
скорость: |
|
|
|
|
υ = |
2gh . |
(2) |
||
Установка
Из рисунка следует, что h = ℓ− ℓcosα = ℓ(1− cosα ) = 2ℓsin2 α2 ,
26

где ℓ - длина нити, α - угол отклонения шара. Если угол отклонения мал, то:
sin2 |
α |
» ( |
α |
)2 |
; |
h = ℓ×( |
α |
)2 |
= |
ℓα 2 |
|
2 |
2 |
2 |
2 |
|
|||||||
|
|
|
|
|
|
|
|
||||
|
|
|
υ = α ℓg . |
|
|
|
|
(3) |
|||
Аналогично можно определить и скорость шаров после удара u,
измерив величину угла их отклонения после удара.
Коэффициент восстановления в этом случае имеет вид:
k= u − (−u) = u .
υ- (-υ) υ
Если учесть соотношение (3) скорости шара и угла его
отклонения, формула упростится:
k = |
u |
= |
α1 |
, |
(4) |
|
υ |
α |
|
||||
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
где α0 - угол отклонения шара до удара, α1 - угол отклонения шара после удара.
Уменьшение угла после первого соударения шаров может оказаться весьма малым. Это вызывает трудности в отсчете угла и приводит к большой погрешности в значении k. Поэтому целесообразно измерить величину угла не после первого соударения, а
после 10 - 15 соударений. Для первого соударения k = α1 , для
α |
0 |
|
27

второго |
k = |
α2 |
, для третьего |
k = |
α3 |
и т.д. Для |
N-го соударения |
|||||||||||
|
|
|
α |
1 |
|
|
|
|
|
|
α |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
k = |
αN |
. Перемножим эти равенства: |
|
|
|
|
|
|
|
|||||||||
αN −1 |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k N = αα1 |
× |
α2 |
× αα3 ××× |
αN |
|
= |
αN |
или |
k = N |
αN |
. (5) |
|||
|
|
|
|
|
|
|||||||||||||
|
|
|
|
α |
α |
|
α |
α |
||||||||||
|
|
|
|
|
0 |
1 |
2 |
|
|
N −1 |
0 |
|
0 |
|
||||
Время соударения τ зависит от относительной скорости шаров, их массы, упругих свойств материала и т.п.; оно может быть измерено на установке.
Если шары соединить в электрическую цепь и подать на них напряжение, то за время их соударения в цепи возникает электрический ток. Время соударения шаров τ может быть отождествлено со временем длительности возникающего прямоугольного электрического импульса. Если включить в цепь электронный осциллограф и подать на один из его входов возникающий импульс при соударении шаров, то на экране осциллографа можно наблюдать данный импульс. Пользуясь шкалой меток осциллографа и зная цену деления каждой метки Т по времени, можно по числу меток Z на импульс определить длительность импульса τ (время соударения) шаров: τ = Z ×T .
Знание коэффициента восстановления k дает возможность вычислить энергию остаточной деформации W.
Закон сохранения энергии для неупругого удара двух шаров запишется в виде:
mυ2 |
+ |
mυ2 |
= |
mu |
2 |
+ |
mu |
2 |
+ 2W , |
|
1 |
2 |
1 |
|
2 |
(6) |
|||||
2 |
2 |
2 |
|
2 |
|
|||||
|
|
|
|
|
|
|
||||
28
где W - энергия остаточной деформации одного шара, |
|
|||||||||||||||||||
относящегося к |
одному |
|
соударению. |
Поскольку |
|
υ1 = −υ2 = υ ; |
|
|||||||||||||
u = −u |
2 |
= u , то получим: |
mυ2 |
= mu2 + 2W , откуда: |
|
|
|
|
|
|||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
W = |
m(υ2 − u |
2 ) |
|
= |
mυ2 |
(1− |
u |
2 |
). |
|
|
|
|
||||
|
|
|
|
|
|
2 |
|
|
2 |
υ |
2 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
u |
|
|
|
|
|
|
|
|
|
|
mυ2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
W = |
|
|
(1− k ). |
(7) |
|
Учитывая, |
что k = υ , |
имеем: |
|
|
|
|
2 |
|||||||||||||
|
|
|
|
|
||||||||||||||||
Зная время соударения шаров, можно рассчитать среднюю силу упругого удара.
|
|
|
|
|
→ |
→ |
→ |
На основании второго закона Ньютона: Fy dt = md υ , где |
Fy - |
||||||
сила упругого удара, действующего на шар. Введем вместо |
Fy |
||||||
|
|
|
|
|
|
|
|
среднюю силу удара F , |
которая в течение |
удара считается |
|||||
→ |
|
|
|
||||
постоянной. Значение F должно удовлетворять равенству: |
|
||||||
τ |
|
|
υ |
|
|
||
∫ |
Fdt = ∫ mdυ |
|
|
||||
0 |
|
|
|
|
−υ |
|
|
(знаки скоростей взяты с учетом их направления относительно вектора силы).
|
|
|
|
|
|||
В результате интегрирования получим: |
Fτ = m(u −υ). |
||||||
|
|
= |
mυ |
(1+ k) . |
|
||
Откуда: |
F |
(8) |
|||||
τ |
|||||||
|
|
|
|
|
|
||
29
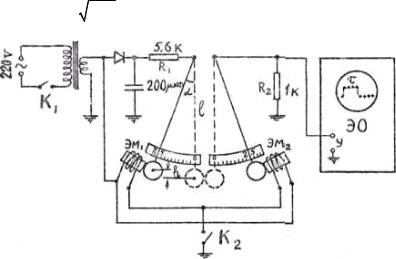
II. Описание установки
На установке два стальных шара расположены на металлических подвесах. Шары удерживаются в отклоненном положении двумя электромагнитами ЭМ1 и ЭМ2,которые могут перемещаться (их положение фиксируются винтами). Углы отклонения шаров отсчитываются по шкале в градусах. Общее питание установки включается тумблером К1, питание электромагнитов включается тумблером К2. При выключении тумблера К2 ток в цепи электромагнитов выключается, шары освобождаются и начинают двигаться друг к другу. При соударении шаров замыкается электрическая цепь, в которую они включены. Поэтому время соударения шаров будет равно длительности электрического импульса, возникающего при их взаимодействии. Напряжение импульса с сопротивлением R2 подается на вход осциллографа. Длительность электрического импульса определяется по экрану осциллографа, работающего в ждущем режиме, с учетом калибровки его длительности по шкале меток электронного осциллографа.
III. Выполнение работы
Предупреждение: при работе на шары подается напряжение 20 В. Прикасаться к шарам и нитям подвески одновременно двумя руками запрещается!
Упражнение 1. Определение коэффициента восстановления k
1.Включить в сеть (220 В) питание установки и питание электронного осциллографа.
2.Включить тумблер осциллографа "сеть". При этом загорится
сигнальная лампочка и через несколько минут на экране осциллографа появится светящаяся точка.
3.Включить последовательно тумблеры питания установки К1 и питание электромагнитов К2.
4.Отвести рукой шары к электромагнитам.
5.Выключить тумблер К2 и начать отсчет соударений. Число ударов (N = 10 - 15) задается преподавателем.
6.Записать угол отклонения шаров после последнего соударения
αN в таблицу. Отсчет угла рекомендуется произвести по обеим шкалам (сначала по одной, затем, повторив опыт, по другой) и брать среднее
30
