Динамическое действие нагрузок (90
..pdf
где t-1 - предел выносливости материала при кручении; ta, tm - амплитудное и среднее напряжения цикла.
Запас выносливости вала при совместном действии изгиба и кручения определяется по эмпирической формуле
n = |
|
nσnτ |
. |
(15) |
|||
|
|
||||||
|
|
n |
2 |
+ n |
2 |
|
|
|
|
|
|
||||
|
|
|
σ |
|
τ |
|
|
Очевидно, что вычисленный запас выносливости должен быть не менее нормативного.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
m |
|
F(t) = F sin θt |
|
||
|
|
|
l/3 |
l/3 |
l/3 |
Рис. 4. Балка с одной степенью
Пример 1
На балку с сосредоточенной массой m действует возмущающая нагрузка
F (t) (рис. 4). Требуется построить эпюру изгибающих моментов от динамического действия нагрузки. Примем следующие исходные
данные: m =1000 кг, жесткость балки EI = 30000 кН×м2, ее длина l = 9 м, отношение частоты вынужденных колебаний к частоте собственных колебаний θ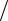
ω = 0,5, амплитудное значение возмущающей нагрузки F =10 кН.
Решение
Найдем частоту свободных колебаний по формуле (1). Перемещение δ11
ищем методом Максвелла– Мора
δ11 = ∫ MEI1 M 1 dz .
Для построения эпюры изгибающих моментов M1 приложим в точке, где расположена сосредоточенная масса, единичную силу по направлению возможного перемещения массы. В данном примере сосредоточенная масса может перемещаться только по вертикали и эпюра моментов от единичной
силы показана на рис. 5. Интегрирование формулы Максвелла– Мора по правилу Верещагина дает:
d = |
1 2l |
× |
l |
× |
1 |
× |
2 |
× |
2l |
+ |
2l |
× |
2l |
× |
1 |
× |
2 |
× |
2l |
12l |
3 |
|
|
( |
|
|
|
|
|
|
|
|
) = |
|
= |
||||||||||
11 |
EI |
9 |
|
3 |
|
2 |
|
3 |
|
9 |
|
9 |
|
3 |
|
2 |
|
3 |
|
9 |
729EI |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
= |
|
|
12 ×93 |
|
= 4 ×10−4 м/кН . |
|
|
||||||||||||
|
|
|
729 |
×30000 |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
а |
|
δ11 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
2/3 |
|
l/3 |
|
|
|
l/3 |
|
|
|
l/3 |
|
|
|
1/3 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
2l/9 |
|
l/9 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Эпюра М1 |
|
|||
б |
1F |
F |
|
||
|
|
|
1/3F |
|
2/3F |
l/3 |
l/3 |
l/3 |
Fl/9 |
|
2Fl/9 |
|
|
Эпюра МF |
Рис. 5. Эпюры изгибающих моментов: а – от единичной силы; б – от амплитудного значения вынуждающей нагрузки F
Обратите внимание на единицы измерения величины δ11 . Подставим δ11
в формулу (1). Вспомним, что 1 кН = 103 Н = 103 кг×м / с2, после подстановки массы m в "кг" получим круговую частоту свободных колебаний в "с–1 ":
ω = |
|
103 |
|
= 50 с-1 . |
|
×10−4 × |
|
||
4 |
1000 |
|||
Теперь определим амплитудное значение силы инерции, используя |
||||||||||||||
формулу (2). Чтобы воспользоваться этой формулой, |
найдем величину |
1F – |
||||||||||||
перемещения по направлению движения массы от амплитудного значения силы |
||||||||||||||
F . В соответствии с методом Максвелла– Мора это перемещение |
|
|||||||||||||
|
|
|
|
D1F |
= |
∫ |
M F M 1 dz . |
|
|
|
||||
|
|
|
|
|
|
|
EI |
|
|
|
|
|
||
Эпюра |
M F |
от действия амплитудного значения |
F показана на рис. 5б. |
|||||||||||
Перемножая эпюры M F и M1 по правилу Верещагина найдем |
|
|||||||||||||
D1F = 1 [ Fl × l × 1 × 2 × 2 l + |
3 |
l |
(2 Fl × 2 l + 2 2Fl × l + |
|
||||||||||
|
|
EI 9 3 2 3 9 |
|
× 6 |
|
9 9 |
|
9 9 |
|
|||||
+ Fl × l + 2Fl × 2 l) + 2Fl × l × 1 × 2 × l ] = 21Fl 3 |
= 35 ×10−4 м. |
|
||||||||||||
9 |
9 |
9 |
9 |
9 |
3 |
2 |
3 |
9 |
1458EI |
|
|
|||
Частота вынужденных колебаний согласно условию |
|
|
||||||||||||
|
|
|
θ = |
θ ω = 0,5 ×50 = 25 с-1. |
|
|
|
|||||||
|
|
|
|
ω |
|
|
|
|
|
|
|
|
|
|
Тогда амплитудное значение силы инерции по формуле (2) |
|
|||||||||||||
|
|
I1 = |
1000 × 35 ×10−4 × 252 |
|
|
|
|
|
|
|||||
|
|
1 |
- 0,52 |
|
|
= 2917 Н = 2,91 кН . |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
Окончательная эпюра изгибающих моментов от динамического действия |
||||||||||||||
нагрузки, показана на рис. 6. |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
I1 = 2,91 кН |
|
|
|
F = 10 кН |
|
|
|
|||||
|
|
|
3 м |
3 м |
|
|
|
3 м |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
Эпюра Мдин , кН×м |
|
||
|
|
|
15,82 |
|
|
22,91 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||
Рис. 6. Эпюра изгибающих моментов от динамического действия нагрузки. |
||||||||||||||
|
B |
Пример 2 |
|
|
|
|
|
|
|
|
|
Q |
4 м |
На раму, показанную на рис. 7, |
падает груз Q с |
||
|
высоты h =15 см. Вес груза Q = 2 кН , поперечное |
||||
h |
|
||||
|
|
|
|
|
|
C |
|
сечение рамы – |
двутавр № |
20. |
Требуется найти |
|
4 м |
максимальные нормальные напряжения в опасном |
|||
|
|
||||
A |
|
сечении рамы и прогиб в точке удара от ударного |
|||
|
|
||||
|
|
действия нагрузки. |
|
|
|
2 м |
2 м |
|
|
|
|
|
|
Решение |
|
|
|
Рис. 7. Рама под |
Чтобы определить динамический коэффициент, |
||||
действием ударной |
необходимо найти прогиб |
δc |
точки С (точки |
||
нагрузки |
приложения нагрузки Q) от статического действия |
||||
|
|
||||
нагрузки. Найдем этот прогиб, используя метод Максвелла– Мора и интегрируя |
|||||
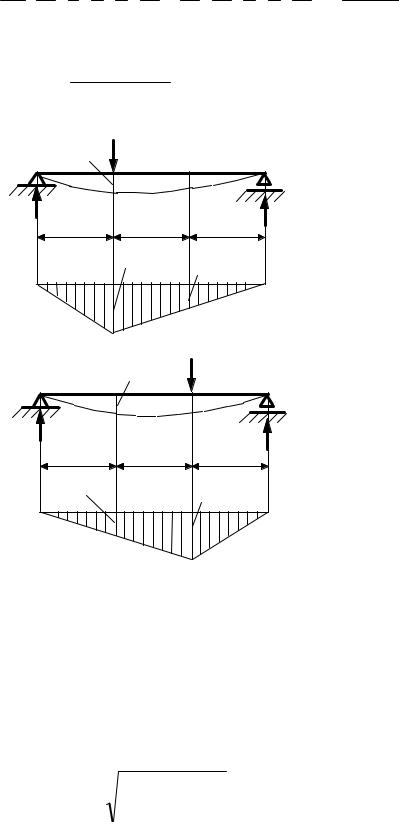
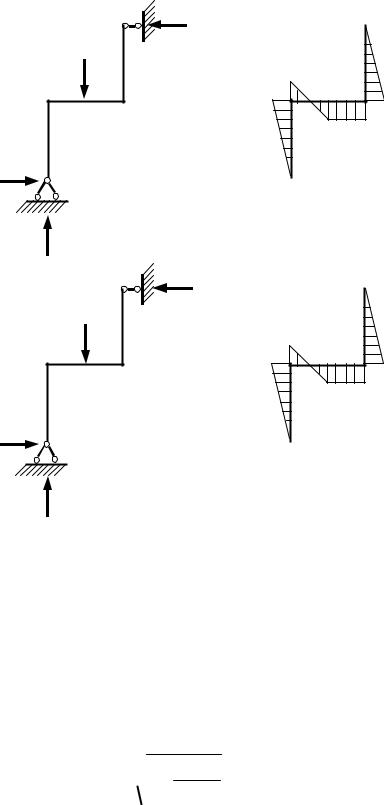
формулу Максвелла– Мора с помощью правила Верещагина. Для этого |
|||||
построим эпюры изгибающих моментов от нагрузки Q и от единичной силы, |
|||||
соответствующей искомому перемещению (рис. 8). Перемножим эти эпюры по |
|||||
правилу Верещагина: |
|
|
|
|
|
δс = |
∫ |
MM 1 |
dz = |
1 |
[ |
2 × 4 |
|
2 |
+ |
2 |
(2 × 2 ×1 + 2 × 2 ×1 - 2 ×1 - 2 ×1)+ |
||||||
EI |
|
|
|
|
|||||||||||||
|
|
EI 2 3 6 |
|
|
|
||||||||||||
|
|
|
+ 2 × 2 ×1 + |
2 × 4 |
|
2 |
] = |
10,67 |
. |
||||||||
|
|
|
|
|
|
||||||||||||
|
|
|
2 3 |
|
EI |
||||||||||||
Подставляя величину жесткости для двутавра № 20, сосчитаем прогиб в "см".
а |
|
|
Q =2 кН |
HB = 1/2 кН |
|
2 |
||
|
2
2
C
2
HA = 1/2 кН
Эпюра M
RA = 2 кН
б
HB = 1/4
1 |
1 |
|
1
1
C
1
HA = 1/4
Эпюра M1
RA = 1
Рис. 8. Эпюры изгибающих моментов а – от веса груза Q; б – от единичной силы
dс = |
10,67 ×106 |
= 0,290 см. |
||
|
×104 |
|
||
|
2 |
×1840 |
||
Найдем динамический коэффициент:
μ = 1 + 
1 + 2 ×15 = 11,22 . 0,290
Определим максимальные нормальные напряжения в опасном сечении от статического действия нагрузки. В рассматриваемом примере несколько
равноопасных сечений с изгибающим |
моментом M max = 2 кН × м. |
|||||||
Максимальные статические напряжения |
|
|
|
|
|
|
||
σmax с = |
M max |
= |
200 |
=1,09 |
кН |
. |
||
|
|
|
||||||
|
Wy |
184 |
|
|
см2 |
|||
Динамические напряжения от действия ударной нагрузки увеличатся в μ
раз:
σmax д = 11,22 ×1,09 = 12,23 кН .
см2
Во столько же раз увеличится и динамический прогиб:
δд = 11,22 × 0,290 = 3,25 см.
Пример 3
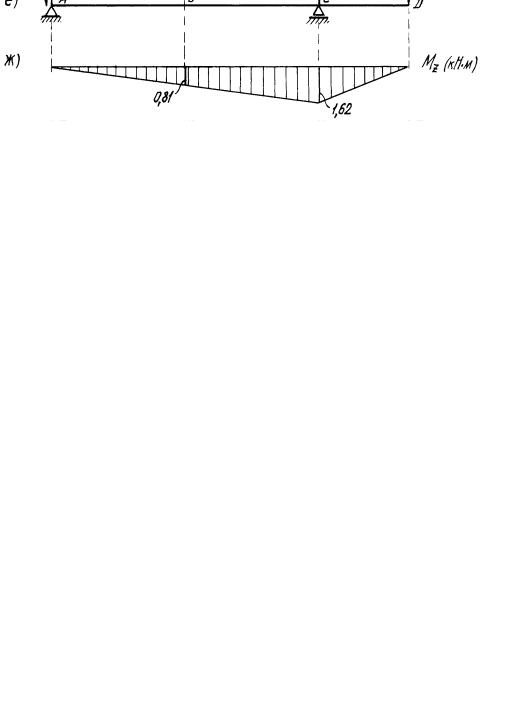
Стальной вал постоянного сечения (рис. 9) вращается с постоянной угловой скоростью n = 120 об/мин и передает через шкив диаметром
D2 = 0,6 м мощность N = 20 кВт. Вал изготовлен из стали марки Ст. 50 с
пределом текучести материала σт = 380 МПа и коэффициентом запаса прочности по отношению к пределу текучести nт=3. Произвести проверку на усталостную прочность вала. В расчете принять, что нормальные напряжения изменяются по симметричному циклу, а касательные - по пульсационному.
Учесть факторы, снижающие предел выносливости: концентрацию напряжений, размеры и способ обработки поверхности детали. Нормативный запас усталостной прочности [n] = 1,5. Обработка поверхности вала - тонкая обточка.
Остальные числовые данные к задаче:
а = 0,3 м; в = 0,3 м; с = 0,2 м; D1 = 0,3 м.
а
б
в
г
д
е
ж
Рис. 9. Стальной вал постоянного сечения, вращающийся с постоянной угловой скоростью
Решение
1.Определение максимальных напряжений в сечении
Для рассчитываемого вала опасным является сечение С, где моменты максимальные (см. рис. 9).
Диаметр вала d = 66 мм =66 × 10 -3 м.
Вычисляем моменты сопротивления сечения вала при его изгибе и кручении:
W |
= pd 3 |
= p(66 ×10−3 )3 |
= 28,2 ×10−6 м3 ; |
изг |
32 |
32 |
|
|
|
||
Wкр |
= pd 3 |
= p(66 ×10−3 )3 |
= 56,4 ×10−6 м3 . |
|
16 |
16 |
|
По эпюрам моментов (рис. 9 в, ж, д) находим крутящий и изгибающие моменты, действующие в сечении С: крутящий момент Mк = 1,62 кНм; изгибающие моменты My = 2,806 кНм и Mz = 1,62 кНм.
Максимальные нормальные напряжения от совместного действия изгибов в двух плоскостях:
|
|
M y2 + M z2 |
(2,806×103 )2 + (1,62 ×103 )2 |
= 114 ×106 |
|
||||||||
smax |
= |
|
|
= |
|
|
|
|
|
|
Па = 114 МПа. |
||
Wизг |
|
|
|
|
28,2 ×10−6 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|||
Максимальные касательные напряжения от кручения |
|
||||||||||||
|
|
tmax |
= |
M к |
|
= |
1,62 ×103 |
= 28,7 ×106 |
Па = 28,70 МПа. |
||||
|
|
|
|
|
|||||||||
|
|
|
|
Wкр |
|
|
56,4 ×10−6 |
|
|
|
|||
2.Определение характеристик циклических напряжений
По условию задачи нормальные напряжения изменяются по симметричному циклу, следовательно
sm = 0; sa = smax = 114 МПа; r = -1.
Касательные напряжения изменяются по пульсационному циклу
tm = ta = 0,5tmax = 0,5 × 28,70 = 14,35 МПа; r = 0.
3.Механические характеристики материала
Необходимые характеристики материала выписываются из справочника: для стали марки Ст.50: sТ = 380 МПа; sв = 700 МПа; s-1 =
300МПа; t-1 = 180 МПа.
4.Вычисление коэффициентов снижения предела выносливости
Из прил. 1 выписываются коэффициенты, необходимые для расчета. Сечение С является опорным, и концентрация напряжений создается прессовой посадкой подшипника.
Используя данные прил. 3 (при σв = 700 МПа и d = 66 мм), путем линейной интерполяции находим
kσ |
= 3,70; |
kτ |
= 2,65. |
|
εσ |
ετ |
|||
|
|
По прил.5 определяем коэффициент влияния качества обработки поверхности при тонкой обточке:
β = 0,85.
Коэффициент чувствительности материала к асимметрии цикла берется из прил.4:
ψτ = 0,05.
Коэффициенты снижения предела выносливости с учетом всех рассмотренных факторов имеют следующие значения:
k |
σд |
= |
|
kσ |
+ |
|
1 |
−1 = 3,7 + |
|
1 |
|
−1 = 3,88; |
|||
εσ |
β |
|
|
|
|||||||||||
|
|
|
|
|
0,85 |
|
|
||||||||
k |
τд |
= |
kτ |
+ |
1 |
|
−1 = 2,65 + |
1 |
|
|
−1 = 2,83. |
||||
|
|
|
|
|
|||||||||||
|
|
ετ |
|
β |
|
|
0,85 |
||||||||
5. Определение запаса усталостной прочности Запас усталостной прочности при изгибе и кручении:
nσ = |
σ−1 |
|
= |
300 |
|
= 0,68; |
|
|
||
kσд s |
|
3,88 ×114 |
|
|
||||||
|
|
а |
|
|
|
|||||
nτ = |
|
|
t−1 |
|
= |
|
|
180 |
= 4,1. |
|
kτд tа |
|
|
|
2,88 ×15 |
+ 0,05 ×14,35 |
|||||
|
+ y τ × tm |
|
||||||||
Запас усталостной прочности при совместном действии изгиба и кручения:
n = |
|
nσnτ |
|
= |
|
0,68 × 4,1 |
|
= 0,67 < [n] = 1,5. |
|
|
|
|
|
|
|||
|
|
nσ2 + nτ2 |
0,682 + 4,12 |
|
|
|||
Запас усталостной прочности вала не обеспечен, так как он меньше нормативного. Диаметр вала необходимо увеличить или ввести упрочняющую обработку.
Примечание. Если опасным является сечение, в котором насажен шкив, то концентрация напряжений создается за счет шпоночной канавки и для определения коэффициентов kσ, kτ, εσ и ετ нужно использовать прил.1 и 3.
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
ЗАДАЧА № 1 «Расчёт на удар»
На балку АВ падает груз весом G с высоты h. Определить наибольшее нормальное напряжение, возникающее в балке. Схемы балок представлены на рис. 10, а числовые данные к задаче необходимо взять из таблицы 1.
|
|
|
|
|
|
Таблица 1 |
|
|
|
|
|
||
Цифра |
Первая цифра зачетной |
Последняя цифра зачетной |
||||
зачетной |
|
книжки |
|
книжки |
||
книжки |
|
|
|
|
|
|
l, м |
|
h, см |
G, кН |
|
№ двутавра |
|
|
|
|
|
|
|
|
1 |
2,1 |
|
2 |
1,3 |
|
22 |
|
|
|
|
|
|
|
2 |
2,0 |
|
4 |
1,2 |
|
24 |
|
|
|
|
|
|
|
3 |
2,3 |
|
5 |
0,9 |
|
24а |
|
|
|
|
|
|
|
4 |
2,5 |
|
7 |
0,8 |
|
27 |
|
|
|
|
|
|
|
5 |
2,6 |
|
9 |
0,6 |
|
27а |
|
|
|
|
|
|
|
6 |
2,2 |
|
11 |
0,4 |
|
33 |
|
|
|
|
|
|
|
7 |
2,4 |
|
3 |
1,1 |
|
30 |
|
|
|
|
|
|
|
8 |
2,6 |
|
8 |
0,9 |
|
40 |
|
|
|
|
|
|
|
9 |
3,1 |
|
6 |
0,3 |
|
24а |
|
|
|
|
|
|
|
0 |
3,2 |
|
12 |
0,5 |
|
36 |
|
|
|
|
|
|
|
ЗАДАЧА № 2 «Свободные и вынужденные колебания балок»
На двух балках двутаврого сечения установлен двигатель весом G, делающий n оборотов в минуту. Наибольшее значение возмущающей силы равно S(t) = S·cosθt. Собственный вес балок и силы сопротивления среды не учитываются.
Требуется определить: