
Поверхностные интегралы. Элементы теории поля. Их приложения в механике и теплотехнике (90
.pdfФедеральное агентство по образованию Государственное учреждение высшего профессионального образования
«Казанский государственный технологический университет» Учебно-методическое управление
ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ. ЭЛЕМЕНТЫ ТЕОРИИ ПОЛЯ. ИХ ПРИЛОЖЕНИЯ К МЕХАНИКЕ И ТЕПЛОТЕХНИКЕ.
Казань
КГТУ
2008
УДК 51 (075.8)
Составители: доц. Бикмухаметова Д.Н. доц. Веселова Л.В.
ст. преп. Гурьянова Г.Б. доц. Ахвердиев Р.Ф. доц Тюленева О.Н.
Поверхностные интегралы. Элементы теории поля. Их прило- жения в механике и теплотехнике: Метод. Указания / Ка- зан.гос.технол.ун-т; Бикмухаметова Д.Н., Веселова Л.В., Гурья- нова Г.Б., Ахвердиев Р.Ф., Тюленева О.Н., Казань.
Приведены необходимые теоретические сведения и ре- шены типовые задачи по теории поля и поверхностным интегра- лам. Методические указания предназначены для студентов вто- рого курса, изучающих дисциплину ЕН.01 «Математика».
Рекомендуется для студентов и преподавателей для орга- низации самостоятельной работы.
Подготовлено на кафедре высшей математики.
Печатается по решению методической комиссии факуль- тета управления и автоматизации КГТУ
Рецензенты: канд. физ-мат. наук Еникеева С.Р. канд. техн. наук Лившиц С.А.
2
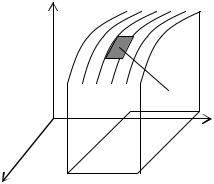
1. Поверхностные интегралы
Поверхностные интегралы являются обобщением двойного интеграла (как и криволинейные интегралы по отношению к оп- ределенному).
1.1. Поверхностные интегралы первого рода
Рассмотрим гладкую поверхность Ω в трехмерном про-
странстве, |
заданную уравнением z = f (x , y) . Разобьем ее про- |
|||||||||||||||||||||
извольным образом на n |
|
z |
|
|
|
|
|
|
|
|
|
|
||||||||||
частей |
с |
площадями |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Si , ( i = 1 , 2 , 3 ,....... n), |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ω |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
обозначив за λ i харак- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
терный |
размер |
каждой |
|
|
|
|
|
|
|
|
|
|
|
|
Si |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
части (например, длины |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
частей). Пусть некоторая |
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
||||||||
|
|
|
F (x , y |
z) |
не- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
функция |
|
|
|
|
|
|
D |
|
|
|||||||||||||
прерывна в каждой точке |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
поверхности Ω . Рас- |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
смотрим |
|
произведение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
вида F (xi |
, yi |
zi ) |
Si , где (xi , yi |
zi )− произвольная точка, |
при- |
|||||||||||||||||
надлежащая i − тому участку поверхности z = |
f (x , y) . |
|
|
|||||||||||||||||||
Определение. |
Если |
при |
стремлении |
λ к нулю, |
|
где |
||||||||||||||||
λ = max λ i |
, существует конечный предел интегральной суммы |
|||||||||||||||||||||
i= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1,n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
zi ) Si , не зависящий от способа разбиения области |
||||||||||||||||||||
∑ F (xi , yi |
||||||||||||||||||||||
i=1 |
|
|
|
|
(xi , yi |
zi ), |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ω и выбора точек |
то этот предел называется по- |
|||||||||||||||||||||
верхностным интегралом первого рода (или интегралом по пло- щади поверхности) и обозначается
3
|
|
|
|
|
|
|
|
n |
, zi ) Si . |
|
||
|
|
∫∫ F (x , y , z) dS = lim ∑ F (xi , yi |
(1) |
|||||||||
|
|
Ω |
|
|
|
|
λ→0 i=1 |
|
|
|||
|
|
Свойства поверхностного интеграла первого рода |
|
|||||||||
1) |
|
∫∫dS = S , где S − площадь поверхности Ω ; |
|
|||||||||
|
|
Ω |
|
|
|
|
|
|
|
|
|
|
2) |
|
∫∫cF (x , y , z) dS = c ∫∫F (x , |
y , z) dS, |
(c = const.); |
|
|||||||
|
|
Ω |
|
|
Ω |
|
|
|
|
|
||
3) ∫∫(F1 (x , y , z)+ F2 (x , y , z)) dS = |
|
|
||||||||||
|
|
Ω |
|
|
|
|
|
|
|
|
|
|
|
|
= ∫∫F1 (x , y , z) dS + ∫∫F2 (x , y , z) dS ; |
|
|
||||||||
|
|
Ω |
|
|
Ω |
|
|
|
|
|
||
4) |
|
∫∫F (x , y , z) dS = ∫∫F (x , y , z) dS + ∫∫F (x , y , z) dS, |
|
|||||||||
|
|
Ω |
|
|
Ω1 |
|
|
Ω2 |
|
|||
|
|
(Ω = Ω1 Ω2 ); |
|
|
|
|
|
|||||
5) Если F1 (x , y |
z) ≤ F2 (x , y |
z), то |
|
|
||||||||
|
∫∫ F1 (x , y , z) dS ≤ ∫∫ F2 (x , y , z) dS ; |
|
|
|||||||||
|
Ω |
|
|
Ω |
|
|
|
|
|
|||
6) |
|
∫∫ F (x , y , z) dS |
|
≤ ∫∫ |
|
F (x , y , z) |
|
dS ; |
|
|
||
|
|
|
|
|||||||||
|
|
|
|
|
|
|||||||
|
|
Ω |
|
|
Ω |
|
|
|
|
|
F (x , y z) непрерывна в |
|
7) |
|
Теорема о среднем. Если функция |
||||||||||
любой точке поверхности Ω , то существует точка (x0 , y0 |
z0 ), |
|||||||||||
такая, что |
|
|
|
|
|
|
|
|
|
|
||
∫∫ F (x , y , z) dS = F (x0 , y0 , z0 ) S ,
Ω
где S − площадь поверхности Ω .
4

Вычисление поверхностных интегралов первого рода
Если Ω – незамкнутая гладкая поверхность, не имеющая кратных точек, а D − ее проекция на плоскость XOY , то по- верхностный интеграл первого рода вычисляется через двойной интеграл по формуле
∫∫ |
F (x , y , z) dS = |
∫∫ |
F (x , y , f (x , y)) |
∂z 2 |
∂z 2 |
|||
|
|
|
|
|
||||
|
|
1+ |
|
+ |
|
dxdy. (2) |
||
Ω |
|
D |
|
|
∂x |
|
∂y |
|
Аналогично можно вычислить поверхностный интеграл первого
рода в случаях, |
когда уравнение поверхности Ω имеет вид |
x = ϕ(y , z) или |
y = ψ (x , z). В первом случае он сводится к |
двойному интегралу по проекции поверхности Ω на плоскость YOZ , во втором случае – по проекции на плоскость XOZ .
Пример 1. Вычислить интеграл по площади поверхности ∫∫ xdS ,
Ω
где Ω - полусфера z = 
 1 − x2 − y2 .
1 − x2 − y2 .
Решение.
Проекция поверхности Ω на плоскость XOY (область D ) – есть круг единичного радиуса с центром в начале координат. Граница области D – окружность x2 + y2 = 1. Вычислим в соот- ветствии с формулой (2)
|
∂z = − |
|
|
|
|
x |
|
|
, |
|
|
∂z |
= − |
|
|
y |
|
|
, |
|||||
|
|
|
|
|
|
|
|
∂y |
|
|
|
|
|
|
||||||||||
|
∂x |
|
|
1 − x2 − y2 |
|
|
|
|
|
|
1 |
− x2 − y2 |
||||||||||||
тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
2 |
|
|
|
|
|
y |
|
|
2 |
|
|
|||
∫∫xdS = ∫∫x |
1+ |
− |
|
|
|
|
|
+ |
− |
|
|
|
|
|
|
dxdy = |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
2 |
|
2 |
|
|
|
2 |
|
2 |
|
||||||||||||
Ω |
|
|
|
|
|
1− x |
− y |
|
|
|
1− x |
− y |
|
|
||||||||||
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
5
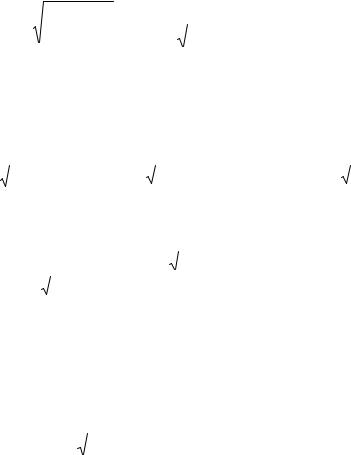
= ∫∫x |
|
|
|
|
1 |
|
|
|
dxdy = |
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
∫∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
dxdy . |
|
|
|
|
|
|
|
|
||||||||||||||
1− x2 |
− y 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
D |
|
|
|
|
|
|
|
|
D 1− x2 − y 2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
Для вычисления полученного двойного интеграла перей- |
|||||||||||||||||||||||||||||||||||||||||||||
дем к |
полярным координатам |
|
|
(r , ϕ ), |
используя |
формулы |
||||||||||||||||||||||||||||||||||||||||
x = r cosϕ , |
y = r sin ϕ , |
|
dxdy = rdrdϕ . При этом |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
r cosϕ |
|
|
|
|
|
|
2π |
|
|
|
|
|
1 |
|
r 2 dr |
|
|
|||||||||||||
∫∫ |
|
|
|
|
|
|
|
|
|
|
|
dxdy = |
∫∫ |
|
|
|
|
|
|
|
|
|
|
rdrdϕ = ∫ cosϕ dϕ |
∫ |
|
|
|
. |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
− x2 − y2 |
|
|
|
|
|
− r 2 |
1 − r 2 |
||||||||||||||||||||||||||||||||||||||
D 1 |
|
|
|
|
|
D 1 |
|
|
|
|
|
|
0 |
|
|
|
|
|
0 |
|
|
|
||||||||||||||||||||||||
Вычислим внутренний интеграл |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
r |
dr |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
r = sin t , 1− r |
|
|
|
= cost |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
∫ |
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= ∫sin |
|
t dt = |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 1− r |
|
|
dr = cos t dt |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
1 |
|
π |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
π |
|
π |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
= |
|
|
|
∫(1− cos 2t )dt = |
|
|
t − |
|
|
sin 2t |
|
|
= |
. |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
2 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
0 |
|
4 |
|
|
|
|
|
|
|
|
|||||||||
Таким образом |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
2π |
|
|
π |
|
|
|
2π |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
∫∫x dS = ∫∫ |
|
|
|
|
|
|
|
|
|
|
dxdy |
= |
|
|
|
∫ cosϕ dϕ = |
|
|
sinϕ |
= |
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
Ω |
|
|
|
|
|
|
D 1− x2 − y 2 |
|
|
|
|
|
|
|
|
|
4 |
0 |
|
|
|
|
|
|
4 |
|
|
|
0 |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
=π (sin 2π − sin 0) = 0. 4
Пример 2. Вычислить интеграл первого рода ∫∫(6x + 4 y + 3z) dS ,
Ω
где Ω – часть плоскости x + 2 y + 3z = 6 , расположенная в пер- вом октанте.
6
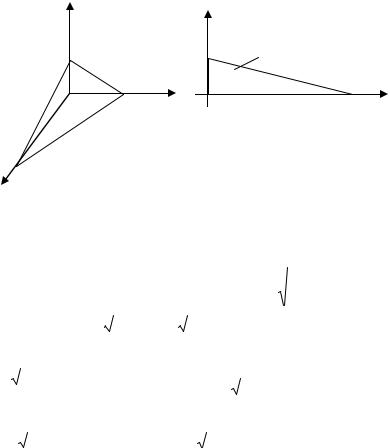
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Поверхность интегрирования Ω – |
|
треугольник ABC , |
ее проек- |
|||||||||||||||||||||||||||||||||||||||||||
ция D на плоскость |
|
|
XOY – |
треугольник OAB . |
Из уравнения |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
C 2 |
|
|
|
|
|
|
|
|
|
|
|
|
B 3 |
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
O |
|
|
|
3 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
x |
|||||||||||
x |
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
плоскости имеем |
z = |
1 |
(6 − x − 2 y), |
|
∂z |
= − |
1 |
, |
∂z |
= − |
2 |
. |
|
|
Тогда из |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
∂x |
3 |
|
∂y |
3 |
|
|
|
|
|
|||||||||||
формулы (2) следует |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
∫∫(6x + 4 y + 3z) dS = ∫∫(6x + 4 y + 6 − x − 2 y) |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
1+ |
1 |
+ |
4 |
|
dxdy = |
|||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||
Ω |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
9 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6−2 y |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
14 |
|
|
|
|
|
|
14 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
= ∫∫(5x + |
2 y + 6) |
|
|
|
|
|
dxdy = |
|
|
|
∫dy |
|
∫ (5x + 2 y + 6)dx = |
|||||||||||||||||||||||||||||||||
|
3 |
|
|
3 |
|
|||||||||||||||||||||||||||||||||||||||||
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(6−2 y ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
14 |
3 |
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
= |
|
|
|
|
∫ |
|
|
x2 + 2xy |
+ 6x |
|
|
|
dy = 2 14 ∫(y 2 −10 y + 21)dy = |
|||||||||||||||||||||||||||||||||
3 |
2 |
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y3 |
2 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
− 5 y + |
|
|
|
|
|
|
= 54 14 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
= 2 14 |
3 |
21y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
1.2. Поверхностные интегралы второго рода
Определение. Гладкая поверхность Ω называется двусто- ронней, если для любой точки M Ω и замкнутого контура L ,
7
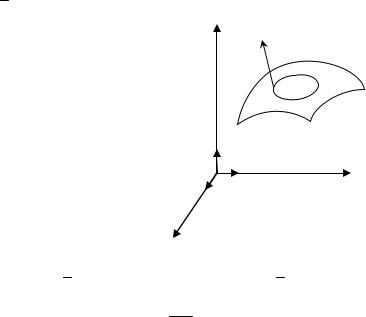
лежащего на поверхности Ω , не пересекающего границы по- верхности и проходящего через точку M, направление нормали n в этой точке после обхода контура L совпадает с исходным.
Если после об- |
z |
|
r |
||
хода по контуру на- |
|
|
n |
||
правление |
нормали |
|
|
Ω |
|
в точке M противо- |
|
|
|
||
положно исходному, |
|
|
M |
||
поверхность называ- |
|
|
|
||
ется односторонней. |
|
r |
|
||
Выберем |
одну |
|
k |
|
|
из сторон |
гладкой |
r |
r |
|
|
двусторонней |
по- |
i |
0 j |
y |
|
|
|||||
верхности |
Ω , |
задав |
|
|
|
одно из двух воз- |
x |
|
|
||
можных |
направле- |
|
|
|
|
нии нормали к ней, то есть введем ориентацию поверхности. Считаем n единичным вектором, тогда n = {cosα , cos β , cos γ }.
Разобьем выбранную сторону поверхности Ω на m частей с площадями Si , ( i = 1 , m) и в каждой из этих частей возьмем произвольную точку M i (xi , yi zi ). Зададим непрерывные на поверхности Ω функции P(x , y , z) , Q(x , y , z) , R(x , y , z) и составим сумму
|
∑m |
P(x , y |
i |
, z |
) |
S yz + Q(x , y |
i |
, z |
) |
S xz + R(x , y |
i |
, z |
) |
S xy , (3) |
||
|
i=1 |
i |
i |
|
i |
i |
i |
|
i |
i |
i |
|
i |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где |
Sixy , Sixz , |
Siyz − площади проекций i- |
части поверхности |
|||||||||||||
Ω |
на координатные плоскости |
|
XOY , XOZ , YOZ соответствен- |
|||||||||||||
но.
Определение. Поверхностным интегралом второго рода (поверхностным интегралом по координатам) от функций
8

P(x , y , z), Q(x , y , z) , R(x , y , z) двусторонней ориентирован- ной поверхности Ω называется предел интегральной суммы (3) при стремлении λ к нулю, если он существует и не зависит от способа разбиения поверхности на части и выбора в них точек M i ( λ = max λ i , где λ i - характерный размер каждой части).
i=1,n
Итак,
∫∫P(x , y , z)dydz + Q(x , y , z)dxdz + R(x , y , z)dxdy =
Ω
= m ( ) + ( ) + ( )
(4)
lim ∑P xi , yi , zi Siyz Q xi , yi , zi Sixz R xi , yi , zi Sixy . λ→0 i=1
Свойства поверхностного интеграла второго рода анало- гичны уже рассмотренным свойствам поверхностного интеграла первого рода.
Необходимо отметить, что поверхностный интеграл второ- го рода меняет знак при смене сторон поверхности интегриро- вания.
Вычисление поверхностных интегралов второго рода сво- дится к вычислению соответствующих двойных интегралов.
Пусть область интегрирования поверхностного интеграла Ω задана уравнением F (x , y , z) = 0 , тогда поверхностный ин- теграл второго рода вычисляется по формуле
∫∫ P(x , y , z)dydz + Q(x , y , z)dxdz + R(x , y , z)dxdy =
Ω |
|
|
= ± ∫∫P(x(y , z), y , z)dydz ± ∫∫Q(x , y(x , z), z)dxdz ± |
(5) |
|
Ω yz |
Ωxz |
|
± ∫∫ R(x , y , |
z(x , y))dxdy , |
|
Ω yz |
|
|
где Ωxy , Ωxz |
, Ω yz − проекции поверхности Ω на |
плоскости |
XOY , XOZ , YOZ соответственно, а x(y , z)- выражение пере-
9
менной |
x через y и z , y(x , z)- выражение переменной |
y че- |
рез x и |
z , z(x , y)- выражение переменной z через x и |
y из |
уравнения поверхности Ω .
Двойной знак в формуле (5) соответствует двум различным сторонам поверхности Ω . Плюс соответствует интегрированию по верхней стороне поверхности Ω (в этом случае угол между нормалью к поверхности и осью OZ - острый).
Пример 3. Вычислить интеграл ∫∫(z − a)2 dxdy по верхней сторо-
|
Ω |
|
|
|
не полусферы x2 + y2 + z 2 = 2az , |
a ≤ z ≤ 2a . |
|
|
|
Решение. |
|
|
|
|
Преобразуем |
уравнение |
поверхности |
к |
виду |
x2 + y2 + (z − a)2 = a2 , откуда z = a + 
 a2 − x2 − y2 .
a2 − x2 − y2 .
10 |
|
8 |
4 |
|
|
6 |
2 |
|
0 |
|
-4 |
|
-2 |
|
-2 |
|
0 |
|
2 |
|
-4 |
|
4 |
Заданная поверхность проецируется на плоскость XOY в |
|
круг x2 + y2 |
≤ a2 (область D ). Тогда |
|
10 |
