Министерство образования и науки Российской Федерации

Калужский филиал федерального государственного бюджетного образовательного учреждения высшего профессионального образования

«Московский государственный технический университет

имени Н.Э. Баумана»

кафедра

Высшая математика

Учебное пособие по курсу аналитической геометрии «Решение типовых задач»

Составил: Влайков Н.Д.

Рецензент: к.ф.-м.н. Савотин А.И.

г. Калуга, 2011 г.

Содержание.

1. Уравнение прямой и плоскости в пространстве стр. 2

2. Уравнения кривых второго порядка стр.7

3. Матричные уравнения стр. 8

4. Решение СЛАУ стр. 10

5. Задачи для самостоятельного решения стр. 14

6. Список рекомендуемой литературы стр. 16

1. Уравнение плоскости и прямой в пространстве.

Даны координаты четырех точек в пространстве .

Найти:

1. Уравнение плоскости, проходящей через точки .

2. Уравнение и длину перпендикуляра, опущенного из т. на плоскость, проходящую через точки .

3. Расстояние от т. до прямой, проходящей через точки .

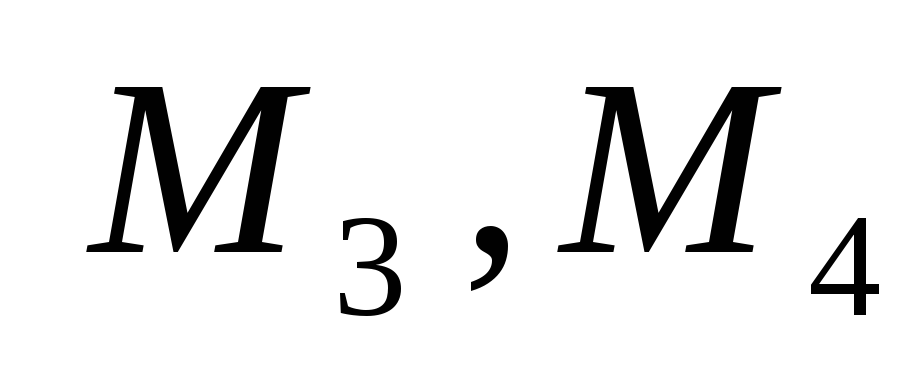4. Точку, симметричную точке , относительно прямой, проходящей через точки .

5. Выполнить чертеж.

Решение.

1.1. Уравнение плоскости, проходящей через три заданные точки, , имеет вид:

. Для наших точек: . Вычислим определитель: следовательно, уравнение искомой плоскости .

1.2. Составим уравнение перпендикуляра, опущенного из т. на плоскость, проходящую через точки . Запишем это уравнение в каноническом виде: , где - координаты точки, принадлежащей прямой, а в знаменателях записаны соответствующие координаты направляющего вектора . Координаты точки, принадлежащей прямой, нам известны. В качестве направляющего вектора, возьмем нормальный вектор плоскости. Т.е. _.

Запишем уравнение перпендикуляра: .

Длина перпендикуляра может быть найдена как расстояние от т. до плоскости по формуле: , где ,,- координаты нормального вектора плоскости, а - координаты точки .

.

1.3. Расстояние от т. До прямой, проходящей через точки .

а) Общий вид уравнения прямой проходящей через две заданные точки ,имеет вид: . Для наших точек:

; ;

б) Теперь найдем расстояние от точки до прямой . Для этого составим уравнение плоскости , проходящей через т. , перпендикулярно прямой . Уравнение плоскости, проходящей через т. , с нормальным вектором имеет вид: .

Координаты т. известны, а в качестве нормального вектора можно выбрать направляющий вектор прямой : . Подставим координаты в уравнение: ; раскрыв скобки и приведя подобные слагаемые получим уравнение плоскости .

в) Найдем координаты точки - точки пересечения прямой и плоскости . Точка - будет являться основанием перпендикуляра опущенного из т. на прямую . Т.к. т. принадлежит и прямой и плоскости, ее координаты должны удовлетворять двум уравнениям, следовательно, координаты можно найти, решив систему:

_;

Для этого перейдем к параметрическому уравнению прямой :

; выразим через параметр :.

Подставим в уравнение плоскости и решим его: ; . Найдем из системы: ;;.

Следовательно, координаты т. .

г) Расстояние от т. до прямой, проходящей через точки можно найти как расстояние между точками и по формуле: .

.

1.4. Найдем координаты т. , симметричной точке , относительно прямой, проходящей через точки . Координаты точки можно найти из условия: т. - середина отрезка (т.к. прямая ). Координаты середины отрезка можно найти по формулам: , , . Следовательно, координаты т.

можно найти так: , , .

Т.е. , , .

.

1.5. Построим несколько поясняющих чертежей:

1.5.1. Построим точки . Для примера построим т.

Рис 1.1 Точка

1.5.2. На рис 1.2 построим плоскость , приведя общее уравнение к уравнению плоскости в отрезках: ; ;

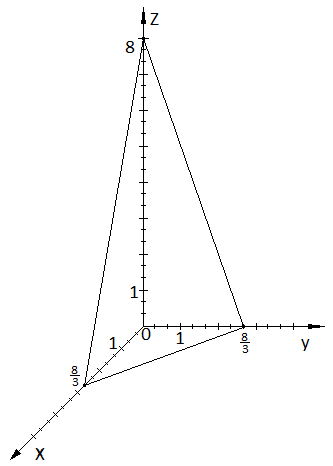
Рис 1.2 плоскость .

1.5.3. Изобразим прямую :

Рис 1.3 прямая

1.5.4. Построим точку :

Рис 1.4 Точка .