Определение коэффициента вязкости жидкости по методу Стокса методические указания к лабораторной работе

Министерство образования и науки РФ

Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования

«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ ЛЕСОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ имени С. М. Кирова»

Кафедра физики

Л а б ор а то р н а я работа № 21

ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ВЯЗКОСТИ ЖИДКОСТИ

ПО МЕТОДУ СТОКСА

Методические указания к лабораторной работе

для студентов всех видов обучения и всех специальностей

Санкт-Петербург

2013

Рассмотрены и рекомендованы к изданию учебно-методической комиссией факультета химической технологии и биотехнологии

Санкт-Петербургского государственного лесотехнического университета 21 декабря 2012 г.

С о с т а в и т е л ь кандидат физико-математических наук, доцент Г. И. Полищук

О т в . р е д а к т о р доктор физико-математических наук, профессор С. М. Герасюта

Р е ц е н з е н т

кафедра физики СПбГЛТУ

Определение коэффициента вязкости жидкости по методу Стокса: методические указания к лабораторной работе / сост. Г. И. Полищук. – СПб.: СПбЛГТУ, 2013. – 12 с.

Методические указания к лабораторной работе по разделу механика предназначены для студентов всех направлений и видов обучения.

Темплан 2013 г. Изд. № 152.

2

§ 1. Ламинарное и турбулентное течения. Вязкость. Ньютоновские жидкости

Различают два типа (режима) течения жидкости: ламинарный и турбулентный.

Ламинарным называют течение, при котором в жидкости можно выделить не перемешивающиеся между собой отдельные слои (струи). Траектории частиц жидкости при ламинарном течении не пересекаются между собой. Пример ламинарного движения – медленное течение равнинной реки.

При достаточно высоких скоростях в ламинарном потоке появляются перемежающиеся колебания струй, которые, нарастая, приводят к тому, что струи разбиваются на нерегулярные, перемешивающиеся между собой более мелкие струйки. Движение частиц жидкости приобретает хаотический, нерегулярный характер. Такой режим течения называют турбулентным. Пример турбулентного движения – движение клубов дыма.

Английский гидродинамик Осборн Рейнольдс в 80-х годах прошлого века установил, что переход из ламинарного режима течения в турбулентный происходит при достижении критического значения некоторого безразмерного числа R, получившего позднее название числа Рейнольдса. Величина его определяется характерной скоростью потока v, характерным размером потока d, плотностью жидкости и величиной коэффициента динамической вязкости η (определение этого коэффициента будет дано ниже):

Для каждого конкретного течения существует свое критическое значение числа Рейнольдса RK . В частности, при обтекании потоком сферы

RK ~ 102 . При R RK течение турбулентно.

При ламинарном течении происходит обмен импульсом между соседними слоями жидкости, которые движутся с различными скоростями. Это приводит к возникновению силы F , противодействующей относительному перемещению соседних слоев: силы, тормозящей более быстрые слои и ускоряющей движение более медленных слоев. Эта сила направлена по касательной к поверхности слоя и называется силой жидкого трения.

Величина, равная отношению F к площади поверхности слоя ∆S,

«Частицей жидкости» в гидродинамике называют малый элемент объема жидкости, содержащий большое число молекул.

3

Измеряется напряжение, как это следует из определения (2), в Н/м2 или в Паскалях. Оно связано с деформацией сдвига, при которой соседние слои сдвигаются один относительно другого.

Во всех реальных жидкостях деформация сдвига сопровождается возникновением касательного напряжения. Это свойство жидкости назы-

вают вязкостью, а напряжение – вязкостным.

В покоящейся жидкости и в однородном потоке вязкостные напряжения отсутствуют.

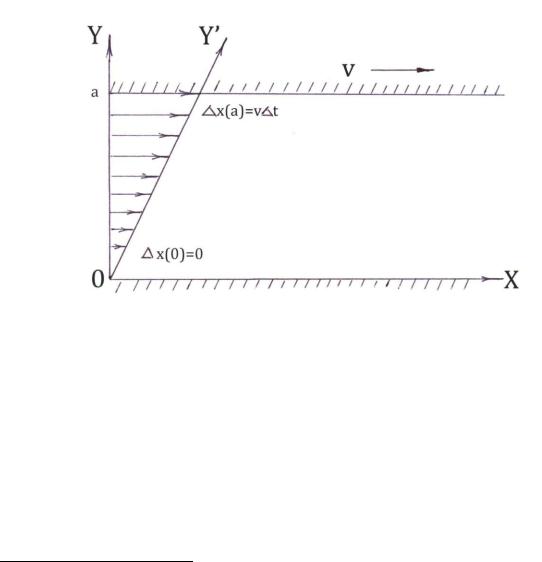
Предположим, жидкость заключена между двумя параллельными стенками, расстояние между которыми а (рис. 1). Если одну из них, например, верхнюю, перемещать параллельно самой себе с постоянной скоростью v, то и тонкий слой жидкости, прилипший к ней, начнет двигаться вместе со стенкой со скоростью v. За счет сил жидкого трения этот слой вовлечет в движение слой, лежащий под ним, который в свою очередь увлечет следующий слой, и т. д. С течением времени придут в движение все слои, за исключением прилипшего к нижней стенке.

Рис. 1

При установившемся режиме течения слои жидкости за время ∆t сдвигаются вдоль оси X на различные расстояния ∆х(у), где ∆х(у) – величина смещения слоя с ординатой у. Эти смещения будут меняться от ∆x(0) = 0 до ∆x(a) = v∙∆t по линейному закону. Частицы жидкости, находящиеся в момент времени t на оси OY, к моменту t + ∆t окажутся расположенными вдоль прямой OY'. Рассматриваемый объем жидкости за это время претерпит деформацию сдвига, которую количественно удобно характеризовать величиной угла YOY'. Этот угол называют углом сдвига и обычно обозначают .

В подавляющем большинстве случаев жидкость прилипает к поверхности твѐрдого тела.

4

Производная от этого угла по времени φ (точка над буквой означает дифференцирование по времени) равна скорости изменения угла, т. е. показывает, сколь быстро осуществляется деформация сдвига. Она называется

Коэффициент пропорциональности – константа, численное значение которой определяется конкретным видом жидкости и зависит от темпера-

туры. Она называется коэффициентом динамической (сдвиговой) вязко-

сти и численно равна величине сдвигового вязкостного напряжения, возникающего между соседними слоями жидкости при единичной скорости деформации сдвига:

/φ

Из последнего соотношения легко установить размерность коэффициента динамической вязкости:

[ ] = [ ] / [ φ ] = Па/с–1 = Па ∙ с = кг ∙ м–1 ∙ с–1.

Здесь квадратные скобки означают, что рассматривается лишь размерность физической величины, заключенной в них. Жидкости, для которых справедливо соотношение (3), т. е. в которых вязкостное напряжение сдвига всюду прямо пропорционально местной скорости сдвига, называют ньютонов-

скими.

К ньютоновским жидкостям относятся многие обычные среды: вода, глицерин, ртуть и т. д. Однако нередко встречаются жидкости с более сложной зависимостью между напряжениями и деформацией. Такие жидкости называют неньютоновскими (к неньютоновским жидкостям относится, в частности, кровь).

§2. Сопротивление, испытываемое сферой, движущейся в ньютоновской жидкости

Предположим, сферическое тело медленно, равномерно и прямолиней-

но движется в безграничной ньютоновской жидкости.

Условие медленности движения означает, что оно характеризуется малым значением числа Рейнольдса (1), в котором в качестве характерного размера d берется диаметр сферы, а в качестве v –скорость тела:

R vd 1.

Очевидно, что R 0 при v 0.

5

Условие безграничности жидкости на практике означает, что размеры сосуда, заполненного жидкостью, значительно больше диаметра сферы, движущейся в этой жидкости.

Рассмотрим два возможных случая.

А. Сфера жесткая, ее поверхность непроницаема для жидкости и на ней выполняется условие прилипания

В этом случае, как показывает опыт, сила сопротивления fC , испыты-

ваемая сферой со стороны жидкости, направлена в сторону, противоположную направлению движения сферы, а величина этой силы fC зависит лишь от коэффициента вязкости жидкости η, радиуса сферы r и величины скорости тела v относительно покоящейся на бесконечности жидкости:

Используя соображения размерности, нетрудно получить явный вид функции (5). Действительно, предположим, что искомая зависимость имеет вид:

где C, , , – неизвестные безразмерные константы. Левая и правая части уравнения (5) должны иметь одинаковые размерности:

[ fC ] [C r v ].

Так как размерность произведения физических величин равна произведению их размерностей, а размерность величины, возведенной в некоторую степень, равна возведенной в ту же степень размерности этой величины, то

[ fC ] [C] [ ] [r] [v] .

Если выразить размерности величин, фигурирующих в последней формуле, через основные единицы системы СИ, получится

кг м с2 кг2 м с .

Это равенство возможно лишь если степени основных единиц измерения, стоящих слева и справа, одинаковы, то есть

1

1. (7)

2

Решая систему (7) относительно , и , получим

= = = 1.

6

Тогда выражение (5) принимает вид fC C rv.

Значение безразмерной константы С примененный метод, называемый методом размерностей, определить не позволяет. Прямым расчетом Стокс установил, что С = 6 . Таким образом, получается формула, выражающая

закон Стокса:

Знак минус указывает, что сила сопротивления направлена против направления движения сферы.

Б. Сферическое тело представляет собой каплю жидкости

В этом случае следует учесть, что на поверхности тела не выполняется условие прилипания. Поэтому при вычислении силы сопротивления формула Стокса (8) должна быть заменена формулой Рибчинского:

На использовании соотношений (8) и (10) основан один из простейших методов определения коэффициента вязкости жидкости. Этот метод получил название метода Стокса.

§ 3. Методика измерения

Исследуемая жидкость помещена в высокий стеклянный цилиндр. В эту жидкость опускают твердый шарик известных размеров, плотность материала которого 1 больше плотности жидкости . На падающий шарик действуют три силы:

1) сила тяжести:

где m1 – масса шарика, g – ускорение свободного падения;

7

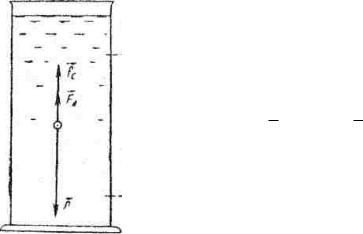
2) выталкивающая сила, равная по закону Архимеда весу жидкости, вытесняемой шариком, и направленная вверх:

где m – масса вытесненной жидкости;

3) сила сопротивления, равная по закону Стокса

. fC 6 rv

Направления этих сил указаны на рис. 2.

Опущенный в жидкость шарик движется сначала ускоренно, так как

P FA fC .

Однако по мере увеличения скорости движения шарика сила fC растет до тех пор, пока не наступит равновесие сил

После этого шарик движется равномерно со скоростью v. Измерив эту скорость, легко найти коэффициент вязкости жидкости . Для этого подставим в формулу (11) соответствующие выражения сил:

43 r3 1g 43 r3 g 6 rv,

откуда получается

Для определения скорости падения шарика v следует измерить время t, за которое шарик проходит расстояние h между двумя метками на цилиндре, расположенными на участке равномерного движения. Тогда

Подставив равенство (13) в выражение (12), получаем окончательную формулу для вычисления коэффициента вязкости:

Настоящая работа может выполняться в двух вариантах. В варианте А наблюдается движение металлического шарика в масле и используется формула (14). В варианте Б наблюдается движение капли воды в масле.

8

Так как вязкость воды значительно меньше вязкости испытуемого масла, то сила сопротивления движению капли может быть вычислена по приближенной формуле (10).

В результате для коэффициента вязкости масла в этом варианте получается следующая формула

где r – радиус капли; ρ1 – плотность воды (ρ1 = (998 ±1) кг ∙ м –3). Остальные обозначения те же, что и в формуле (14). Получите формулу (15) самостоятельно.

§4. Порядок выполнения работы

Ва р и а н т А

1.Взять пять одинаковых металлических шариков. Измерить с помощью микрометра их диаметры d. Используя среднее значение диаметра шарика dср вычислить объем одного шарика V.

2.Взвесить пять шариков на аналитических весах. Вычислить среднее значение массы одного шарика m1. Определить плотность материала ша-

рика ρ1 = m1 / V.

3.Измерить линейкой расстояние h между метками на цилиндре с испытуемым маслом.

4.Опустить шарик в масло и измерить по секундомеру время t, за которое он пройдет расстояние h. Повторить это измерение еще с четырьмя шариками и определить среднее время движения шарика.

5.Измерить плотность масла ρ с помощью ареометра.

6.Результаты измерений заносить в табл. 1 и 2.

7.Вычислить коэффициент вязкости по формуле (14), используя

средние значения dср и tср. Указать температуру, при которой произведено измерение.

8.По общим правилам оценить погрешность измерения коэффициента

вязкости ∆ .

9. Вычислить значение числа Рейнольдса для падающего в масле шарика. Оправдано ли использование закона Стокса в Вашем эксперименте?

Не забывайте при вычислениях переводить все величины в одну систему единиц!

9

Ва р и а н т Б

1.Взвешиванием на аналитических весах определить массу часового

стекла М1.

2.Из капельницы, помещенной над сосудом с маслом, накапать в это

стекло N капель воды (N = 30–40). Определить массу М2 стекла с водой и массу N капель воды М:

М= М2 – М1.

3.Подсчитать массу одной капли т1. Вычислить радиус капли

4.Измерить линейкой расстояние h между метками на цилиндре с маслом.

5.Добиться медленного вытекания капель из капельницы. Капли не должны разбиваться при ударе о поверхность масла (капельница не должна находиться слишком высоко над уровнем масла).

6.Измерить по секундомеру время t, за которое одиночная капля проходит расстояние h. Повторить это измерение с пятью каплями и найти среднее время движения капли tcp.

7.Измерить ареометром плотность масла .

8.Результаты всех измерений заносить в табл. 2 и табл. 3.

9.Вычислить значение коэффициента вязкости по формуле (15), ис-

пользуя среднее значение tср. Указать температуру, при которой производились измерения.

10.По общим правилам оценить погрешность измерения коэффици-

ента вязкости ∆ .

11. Оценить величину δ, стоящую в формуле (9). Оправдано ли применение в Ваших расчетах приближенной формулы (10)? ( 1 10–3 Па ∙ с

при 20°С).

10