УДК 53.51 ББК 22.311 М 54

Печатается по решению редакционно-издательского совета Башгоспедуниверситета

Методы математической физики: Сборник задач /сост. З.В.Гареева.

– Уфа: Изд-во БГПУ, 2005, – 20с.

Сборник содержит задачи и упражнения по основным разделам курса «Методы математической физики»: элементам теории поля, уравнениям математической физики, специальным функциям. В сборнике представлены как тренировочные задачи, направленные на закрепление основных формул и методов решения, так и комбинированные задачи, способствующие выявлению взаимосвязей между различными темами и разделами. В начале каждого раздела приводятся необходимые теоретические сведения, в конце сборника даются ответы ко всем предложенным задачам.

Сборник задач предназначен для использования на практических занятиях по предмету «Методы математической физики», для самостоятельной работы студентов физико-математических специальностей вузов.

Составитель З.В. Гареева, к.ф.-м.н., ст.преподователь

Рецензенты: Е.С.Шиховцева, д-р ф.-м.н.; Ф.Г.Мукминов, д-р ф.-м.н.

© Издательство БГПУ, 2005

2

rr r

1.15.Вычислить div( a ×(r ×b) ) .

1.16.Вычислить градиент потенциала электростатического поля,

1.19.Доказать, что rot(a1+a2)=rota1+rota2

1.20.Представить a ×gradϕ , где а- постоянный вектор, в виде вихря

некоторого вектора.

1.21. Вычислить n [grad(a n) −rot(a ×n)], где а- переменный вектор, n- единичный постоянный вектор.

2. Вводные понятия. Классификация уравнений с частными производными. Приведение к каноническому виду уравнений с частными производными второго порядка с двумя независимыми переменными

Задачи

Выяснить являются ли приведенные ниже равенства дифференциальными уравнениями с частными производными. Выяснить какие из них являются линейными (однородными, неоднородными), нелинейными, казилинейными

2.1.uxx2 +uyy2 −(uxx +uyy )2 = 0 .

2.2.ln(ux uy ) −ln(ux ) −ln(uy ) +5u −6 = 0 .

2.3.sin(uxx2 +uy ) +cos(uxx +uxy ) = 0 .

2.4.uxuxy2 +2xuuyy −3xyuy −u = 0 .

2.5.3uxy −6uxx +7uy −ux +8x = 0 .

2.6.uxy +uy +u2 − xy = 0 .

2.7.2 sin(x + y)uxx − x cos yuxy + xyux −3u +1 = 0 .

2.9. uy uxx −3x2uuxy + 2ux − f (x, y)u = 0.

5

2.10. 2sin(x + y)uxx − x cos yuxy + xyux −3u +1 = 0 .

Определить тип следующих уравнений

2.11.uxx + 4uxy +uyy +ux +uy + 2u − x3 y = 0 .

2.12.2uxx + 2uxy +uyy +ux +uy − 2u = 0 .

2.13.uxx + 2uxy +uyy +ux +uy +3u − xy2 = 0 .

2.14.4uxx + 6uxy + 2uyy +uy + 2u = 0 .

2.15.12uxx + 3uyy + xy + uy − 2u = 0 .

2.16.uxx + 2uxy −6uyy +uy − 2u = 0 .

2.17.12uxx +12uxy + xyux + yuy = 0 .

2.18.uxx − 6uxy −3uyy + xux + yuy = 0 .

2.19.8uxy +uyy − 2xyu = 0 .

2.20*. Найти области гиперболичности, эллиптичности и параболичности уравнения (l + x)uxx + 2xyuxy − y2uyy = 0 и исследовать их зависимости от l, где l- числовой параметр.

Привести к каноническому виду следующие уравнения

2.21.x2uxx − y2uyy = 0 .

2.22.x2uxx + 2xyuxy + y2uyy = 0, x > 0 .

2.23.uxx + 4uxy +5uyy = 0 .

3.Физические задачи, приводящие к уравнениям гиперболического типа; постановка краевых задач

3.1.(Малые колебания струны) Струна натянута с силой Т0 и находится в прямолинейном положении равновесия; ее концы неподвижно закреплены. В момент t=0 точкам струны сообщаются начальные отклонения и скорости. Поставить краевую задачу для определения малых отклонений точек струны при t>0.

3.2.(Продольные колебания стержня) Упругий прямоугольный стержень выведен из состояния покоя тем, что его поперечным сечениям в момент времени t=0 сообщены малые продольные смещения и скорости. Предполагая, что поперечные сечения стержня все время остаются плоскими, поставить краевую задачу для определения смещений поперечных сечений стержня при t>0. Рассмотреть случаи, когда концы стержня:

а) закреплены жестко б) двигаются в продольном направлении по заданному закону

6

в) закреплены упруго, т.е. каждый из концов испытывает со стороны заделки продольную силу, пропорциональную смещению и направленную противоположно смещению.

3.3.Вывести телеграфное уравнение.

3.4.(Волны тяжелой жидкости в канале). В неглубоком горизонтальном канале длины l с прмоугольным поперечным сечением находится вода, глубина которой , отсчитанная от свободной покоящейся поверхности, равна h. Концы канала закрыты плоскими жесткими перегородками, перпендикулярными к его образующим. Направим ось x вдоль канала. При небольших возмущениях свободной поверхности в канале может возникнуть волновое движение воды, при котором

поперечные сечения, состоящие из жидких частиц будут, как целые, получать смещение ξ(x,t) вдоль оси x, а их высота будет получать отклонение η(x,t) от высоты h свободной покоящейся поверхности воды.

Пусть заданы начальные значения ξ(x,t) и η(x,t) в момент времени t=0. Поставить краевую задачу для определения ξ(x,t) и η(x,t) при t>0.

3.5.К струне, концы которой закреплены неподвижно, начиная с момента t=0, приложена непрерывно распределенная сила, линейная плотность которой равна F(x,t). Поставить краевую задачу для определения поперечных отклонений u(x,t) точек струны при t>0.

3.6.Поставить краевую задачу о поперечных колебаниях тяжелой струны относительно вертикального положения равновесия, если ее верхний конец жестко закреплен, а нижний свободен.

3.7.Два полуограниченных однородных упругих стержня с одинаковыми

поперечными сечениями соединены торцами и составляют один неограниченный стержень. Пусть ρ1, E1-плотность массы и модуль упругости одного из них, а ρ2, E2 – другого. Поставить краевую задачу для определения продольных отклонений поперечных сечений неограниченного стержня от их положений равновесия, если в начальный момент времени поперечным сечением стержня сообщены некоторые продольные смещения и скорости.

3.8.В некоторой точке неограниченной струны прикреплен шарик массы М, а к нему прикреплена пружинка с коэффициентом упругости k и осью, перпендикулярной к равновесному положению струны. Поставить краевую задачу о поперечных колебаниях струны. Рассмотреть также случай, когда

шарик испытывает сопротивление пропорциональное скорости с коэффициентом пропорциональности k*.

4.Уравнение колебаний струны

4.1. Метод Даламбера

Метод Даламбера широко используется для решения уравнений колебаний струны.

7

4.2.Задачи для бесконечной струны

Найти решение уравнения

4.1.1.utt = uxx , если u(x,0) = x2 ,ut (x,0) = 0

4.1.2.utt = 4uxx если u(x,0) = 0,ut (x,0) = x

4.1.3.если u(x,0) = 0,ut (x,0) = cos(x)

4.1.4.utt = uxx если u(x,0) = x,ut (x,0) = −x

4.1.5.utt=4uxx, u(x,0)=0;ut=e2x; u(x,t)-?

4.1.6.utt=16uxx, u(x,0)=sin(2x);ut=cos(2x); u(x,t)-?

4.1.7.utt=9uxx, u(x,0)= e2x ;ut=0; u(x,t)-?

4.1.8.utt=9uxx, u(x,0)=x+1;ut=0; u(x,t)-?

4.1.9.Найти форму струны, определяемой уравнением utt = a2uxx в момент

времени t=π/(2a), если u(x,0)=sin(x), ut(x,0)=1.

4.1.10. Найти форму струны, определяемой уравнением utt = uxx в момент времени t=π, если u(x,0)=sin(x), ut(x,0)=cos(x).

4.1.11.utt=uxx, u(x,0)=sin(x);ut=0; u(x,t)-?

4.1.12.utt=uxx, u(x,0)=sin(x);ut=x/(1+x2); u(x,t)-?

4.1.13.utt=uxx, u(x,0)=x ;ut=sin(x) ; u(x,t)-?

4.1.14.utt=uxx, u(x,0)=x ;ut=cos(x) ; u(x,t)-?

15.utt=uxx, u(x,0)=e-x ;ut=x/(1+x2) ; u(x,t)-?

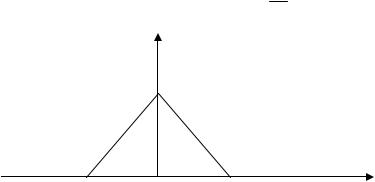
16.Неограниченная струна возбуждена локальным начальным отклонением, изображенным на рис.1. Построить (начертить) положение

струны для моментов времени tk = 4kca , где k=0,1,2,3,5. u

x

рис.1.

8

4.3. Задачи для полубесконечной струны

удовлетворяющие условиям u(x,0)=e-x , ut(x,0)= sin(x), u(0,t)=0.

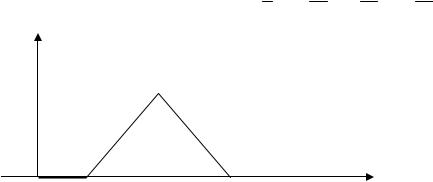
4.2.7. Полуограниченная струна, закрепленная в конце, возбуждена начальным отклонением, изображенным на рис. 2. Начертить положение струны для моментов времени t = ac , t = 23ca ,t = 2ac , t = 27ac

u

x

рис. 2.

4.2.8.utt=4uxx, u(x,0)=ln(x), ut(x,0)=0,u(0,t)=0, u(x,t)-?

4.2.9.utt=uxx, u(x,0)=0, ut(x,0)=sin(x),u(0,t)=0, u(x,t)-?

4.4.Задачи для конечного отрезка струны. Решение уравнения колебания струны методом Фурье

Согласно методу Фурье решение уравнения utt=a2uxx, удовлетворяющее начальным условиям u(x,0)=ϕ(x), ut(x,0)=ψ(x) и граничным условиям u(0,t)=0, u(l,t)=0 может быть представлено суммой бесконечного ряда

9

Задачи

4.3.1. Струна, закрепленная на концах x=0, x=l, имеет в начальный момент форму параболы u = 4l2h x(l − x) . Определить смещение точек струны от оси

абсцисс, если начальные скорости отсутствуют (рис.1). u

h

рис.1.

4.3.2. Дана струна, закрепленная на концах x=0, x=l. Пусть в начальный момент форма струны имеет вид ломаной ОАВ, изображенной на рис.2. Найти форму струны для любого момента времени t, если начальные скорости отсутствуют.

u

A

h

рис. 2.

4.3.3. Пусть начальные отклонения струны, закрепленной в точках x=0, x=l, равны 0, а начальная скоростьвыражается формулой

любого момента времени t.

4.3.4.Струна, закрепленная на концах x=0, x=l, имеет в начальный момент форму u=h(x4-2x3+x). Найти форму струны для любого момента времени t, если начальные скорости отсутствуют.

4.3.5.Струна закреплена в точках x=0 и x=l. Начальная скорость выражается формулой

для любого момента времени t.

10