Геометрическое определение вероятности

Классическое определение вероятности применимо, когда число исходов опыта конечно. Если опыт имеет бесконечное множество несовместных равновозможных исходов, которые можно сопоставить с точками области G, то вероятность события А определяется формулой

.

Здесь  – это мера (длина, площадь или объем) области; g – это область, соответствующая исходам, благоприятствующим А, и содержащаяся в G.

Для иллюстрации случайных событий удобно изображение исходов опыта в виде области на плоскости. Например, хорошо иллюстрируются совместные и несовместные события. На рис. 1.1 изображены множества исходов g(A) и g(B), благоприятствующие несовместным событиям А и В, а на рис. 1.2 – совместным.

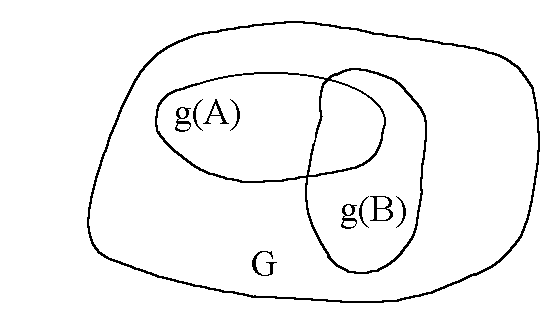
Рис. 1.1. Рис. 1.2.

Рассмотрим на примере использование геометрического определения вероятности.

Пример 1.6. Известно, что автобус № 5 отправляется с остановки строго по расписанию каждые 20 минут. Пассажир, который не знает расписания, приходит на остановку. Какова вероятность того, что он будет ждать автобус не более двух минут.

Решение. В этой задаче можно считать, что приход человека на остановку (испытание) будет равновозможным в любой момент времени двадцатиминутного интервала между приходами автобуса. Следовательно, каждый исход опыта сопоставим с точкой отрезка G = [0, 20] на числовой оси. Пусть событие А – приход на остановку пассажира не более чем за две минуты до появления автобуса. Исходы, благоприятствующие событию А, соответствуют точкам отрезка g = [18, 20] на числовой оси. Вероятность события А равна отношению длины отрезка g = [18, 20] к длине отрезка G=[0, 20], то есть

P(A) = .

Классическое и геометрическое определения вероятности применимы лишь в случае, когда событие может появиться в опыте, имеющем равновозможные исходы. Но достаточно часто это не выполнено. Поэтому классическое и геометрическое определения вероятности здесь не могут быть применены.

Статистическое определение вероятности

Пусть событие А появляется в результате опыта, который можно повторять сколь угодно большое количество раз. Предположим, что проведено N опытов и событие А появилось в М опытах. Относительной частотой события А в проведенных опытах называют число

W(А) = .

Очевидно, в разных сериях опытов значения относительной частоты, как правило, различны. Однако при многократном повторении серий опытов с увеличением числа опытов в сериях значения W(А), меняясь, сгущаются около некоторого значения. Его называют статистической вероятностью события А.

Для подтверждения правомочности такого определения математики рассматривали в качестве А – появление герба при бросании монеты (Р(А) = 0,5 по классическому определению вероятности). Они провели множество серий бросков и получили следующие результаты:

Автор	N	M	W(A)=M/N
Бюффон Феллер Джевонс Пирсон	4040 10000 12000 24000	2048 4979 6019 12012	0.5069 0.4979 0.5016 0.5005

Итак,

Подчеркнем, что относительная частота может быть найдена только после проведения серии испытаний, тогда как вероятность вычисляется до проведения испытания. Так, например, если стрелок сделал 100 выстрелов и из них 75 раз поразил цель, то относительная частота события А = {попадание в цель при одном выстреле} будет равна

Это число и будет рассматриваться как  вероятность попадания в цель при одном выстреле.

Пример 1.7. Замечено, что из 70 плодовых деревьев приживается на другой год 50. Сколько надо посадить деревьев, чтобы прижилось 120?

Решение. Испытание в данном случае  посадка дерева. В серии из 70 испытаний событие А = {дерево прижилось} наступило 50 раз. Следовательно, Число М появлений события А в серии из N испытаний по условию равно 120. Поэтому значение N определим из равенства

откуда

ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ К ТЕМЕ 1

Задача 1.1. Подброшены три игральные кости. Найти вероятность того, что сумма очков на верхних гранях будет:

Вариант	Сумма очков на верхних гранях	Вариант	Сумма очков на верхних гранях
1	меньше пяти	16	нечетная
2	кратна пяти	17	четная
3	больше пятнадцати	18	меньше девяти
4	хотя бы семнадцать	19	не меньше десяти
5	кратна шести	20	кратна девяти
6	меньше шести	21	больше десяти
7	не больше семи	22	меньше одиннадцати
8	хотя бы шестнадцать	23	не больше пяти
9	кратна семи	24	не больше десяти
10	не больше семи	25	больше четырнадцати
11	не меньше восьми	26	хотя бы одиннадцать
12	хотя бы девять	27	кратна четырем
13	кратна восьми	28	не больше четырех
14	не больше восьми	29	больше тринадцати
15	меньше девяти	30	кратна девяти

Задача 1.2. Слово составлено из карточек, на каждой из которых написана одна буква. Затем карточки перемешаны и случайным образом выстроены в линию. Какова вероятность, что в результате образовано прежнее слово?

Вариант	Слово	Вариант	Слово
1	Геометрия	16	Аббревиатура
2	Геодезия	17	Ботаника
3	Программа	18	Броненосец
4	Землепользование	19	Бюллетень
5	Землеустройство	20	Бюрократия
6	Вероятность	21	Вагоновожатый
Вариант	Слово	Вариант	Слово
7	Преобразование	22	Теодолит
8	Грамматика	23	Опровержение
9	Вычисление	24	Ветеринария
10	Калькулятор	25	Винегрет
11	Производная	26	Парабола
12	Систематика	27	Горизонт
13	Синтаксис	28	Графология
14	Орфография	29	Масштаб
15	Абстракция	30	Население

Задача 1.3. На складе имеется k инженерных и l бухгалтерских микрокалькуляторов в одинаковых упаковках. Случайным образом берут m упаковок. Найти вероятность того, что в них окажется:

а) n инженерных микрокалькуляторов;

б) меньше чем n инженерных микрокалькуляторов;

в) хотя бы один инженерный микрокалькулятор.

Вариант	k	l	m	n	Вариант	k	l	m	n
1	5	6	5	3	16	7	4	5	3
2	6	5	4	2	17	5	7	4	3
3	6	5	5	3	18	6	5	5	2
4	7	4	4	2	19	5	7	5	4
5	4	5	4	2	20	6	7	5	3
6	8	6	5	3	21	6	8	5	4
7	6	7	4	4	22	6	5	5	4
8	4	7	4	2	23	8	6	5	3
9	5	6	5	3	24	6	7	4	3
10	7	4	4	2	25	5	7	4	2
11	8	6	4	3	26	6	7	6	3
12	6	5	4	3	27	5	7	5	3
13	4	6	4	3	28	6	8	5	3
14	8	6	5	2	29	6	7	5	2
15	5	6	5	4	30	4	7	4	2