
9
способами можно выдать некоторой студенческой группе 3 билета в театр и 4 билета в филармонию?
34. Сколько можно образовать различных инициалов, если каждый человек имеет одну фамилию, имя, отчество?
35. Пять девушек и трое юношей играют в городки. Сколькими способами они могут разбиться на две команды по 4 человека, если в каждой должно быть хотя бы по одному юноше?
36. Даны натуральные числа от 1 до 30. Сколькими способами можно выбрать три числа так, чтобы их сумма была чётной?
1.2. Классическое и статистическое определения вероятности. Геометрическая вероятность
Согласно классическому определению, вероятность события А вычисляется
по формуле Р(А) = |
m |
, |
(1.7) |
|
n |
||||
|
|
|
где n – число всех равновозможных, единственно возможных и несовместных исходов испытания; m – число исходов, благоприятствующих появлению события А. Таким образом, нахождение вероятности события сводится к вычислению значений параметров n и m, а так как 0 ≤ m ≤ n, то 0≤ Р(А) ≤ 1.
Статистической вероятностью события |
А называют относительную частоту |
||
появления этого события в n |
произведённых испытаниях, т.е. |
||
( А) |
m |
, |
(1.8) |
|
|||
|
n |
|
|
где m – число испытаний, в которых появилось событие А n – общее число испытаний.
Пример 1.9. Имеется 100 одинаковых деталей, среди которых 3 бракованных. Найти вероятность того, что взятая наудачу деталь окажется без брака.
Решение. В этой задаче производится испытание – извлекается одна деталь. Число всех исходов испытания равно 100, т.к. может быть взята любая деталь из 100. Эти исходы несовместные равновозможные и единственно возможные. Таким образом, n = 100. Событие А состоит в появлении детали без брака. Всего в партии 97 деталей без брака, следовательно, число исходов,

10
благоприятных появлению события А равно 97. Итак, m = 97, тогда
97 Р( А) 0,97
100
Пример 1.10. Код банковского сейфа состоит из 6 цифр. Найти вероятность того, что наудачу выбранный код содержит различные цифры.
Решение. Так как на каждом из шести мест в шестизначном номере может стоять любая из десяти цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, то всех различных шестизначных номеров, по правилу произведения, будет равно n = 10 10 10 10 10 10 = 106. Номера, в которых все цифры различны,  это размещения из 10 элементов по 6. Поэтому число благоприятных исходов
это размещения из 10 элементов по 6. Поэтому число благоприятных исходов
6 |
|
|
|
А106 |
10 9 8 7 6 5 |
= 0,1512 . |
||
m= А10 |
. Искомая вероятность равна P( A) |
|
|
|
|
|
||
6 |
6 |
|
||||||
|
|
|
10 |
10 |
|
|
||
Пример 1.11. |
Группа туристов из 15 юношей и 6 |
девушек выбирают по |
||||||
жребию хозяйственную команду в составе пяти человек. Какова вероятность, что в составе команды окажутся три юноши и две девушки ?
Решение. Испытание состоит в том, что из двадцати одного человека выбирают пятерых. Так как выбор осуществляется по жребию, то все исходы испытания равновероятны и, кроме того, они не совместны. Число исходов испытания n C215 , так как выборка состоит из пяти элементов и порядок их расположения в выборке не учитывается.
Пусть событие А состоит в том, что в составе выбранных окажутся три
юноши и две девушки. Трёх юношей из 15 |
можно выбрать C3 |
способами, и |
||||||||||
|
|
|
|
|
|
|
|
|
15 |
|
|
|
после каждого такого выбора двух девушек из 6 можно выбрать С 2 |
способами. |
|||||||||||
|
|
|
|
|
|
|
|
|
|
6 |
|
|
По правилу произведения, |
событию |
А |
благоприятствует С3 С2 |
исходов |
||||||||
|
|
|
|
|
|
|
|
|
|
15 |
6 |
|
испытания. Искомая вероятность равна |
P( A) |
|
C 3 C 2 |
0,217 . |
|
|
|
|||||
15 |
6 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
C215 |
|
|
|
|
|
|
Задачи |
|
|
|
|
|
|
|
|
|
|
|
|
37. |
Укажите, |
какие |
из |
следующих |
событий |
|
|
являются: |
||||
1) случайными; 2) достоверными; 3) невозможными: |
|
|
|
|
||||||||
а) выигрыш по одному билету лотереи спортлото; б) извлечение из урны цветного шара, если в ней находится 3 синих и 5 красных шаров; в) извлечение бракованного изделия из партии годных изделий; г) получение студентом 25 баллов при сдаче 4 экзаменов, если применяется пятибалльная система оценок; д) выпадение не более шести очков на верхней грани игрального кубика.
38. Какова вероятность того, что последняя цифра наугад набранного
11
телефонного номера окажется равной 5 или кратной 3?
39. Подбрасываются две игральные кости. Какова вероятность того, что сумма выпавших очков будет не больше 5?
40. Какова вероятность того, что число на вырванном наудачу листке нового календаря: а) кратно 2; б) равно 29, если в году 365 дней.
41. В группе 6 юношей и 18 девушек. По жребию разыгрывается один билет в театр. Какова вероятность того, что билет достанется девушке?
42. В партии 5 изделий первого сорта и 7 – второго. Какова вероятность, что наудачу взятое изделие будет: а) первого сорта; б) второго сорта.
43. Жюри конкурса определило 10 претендентов, одинаково достойных первой премии. Среди них оказалось 2 студента 4-го курса, 4 студентов 5-го курса, 4 аспиранта. Какова вероятность того, что в результате жеребьёвки
премия будет выдана студенту? |
|
|
44. В ящике 15 деталей, среди которых 9 |
стандартных. |
Сборщик наудачу |
извлекает три. Найти вероятность того, что |
извлечённые |
детали окажутся: |
а) стандартными; б) нестандартными? |
|
|
45. Из 25 студентов 8 имеют спортивные разряды. Какова вероятность, что выбранные наудачу 4 студента: а) имеют спортивный разряд; б) не имеют спортивного разряда.
46. Магазин получает товар партиями по 50 штук. Если пять взятых наудачу образцов соответствует стандартам, партия товара поступает на реализацию. В очередной партии 4 единицы товара с дефектом. Найти вероятность того, что товар поступит на реализацию?
47. Из колоды (36 карт) наудачу вынимают 6 карт. Найти вероятность, что среди них окажется один туз?
48.В компании 11 акционеров, из них три имеют привилегированные акции. На собрание акционеров явилось 6 человек. Найти вероятность того, что среди явившихся акционеров: а) все трое акционеров с привилегированными акциями отсутствуют; б) двое с привилегированными акциями.
49.Служащие компании распределены в таблице по отделам и полу.
Подразделение |
Женщины |
|
Мужчины |
|
|
|
|
Производственный отдел |
|
6 |
20 |
Ремонтная мастерская |
|
3 |
10 |
Склады |
|
5 |
5 |
Автобаза |
|
2 |
8 |
Отдел реализации |
|
5 |
10 |
|
|
|
|
12
В компании решено организовать комиссию по охране труда из 5 человек. Какова вероятность, что : а) все члены комиссии женщины; б) члены комиссии работники разных отделов; в) в комиссию не войдут работники отдела реализации; г) в состав комиссии войдут женщина, работающая на складе, 2 работника производственного отдела и двое мужчин, работающих в ремонтной мастерской.
50. В партии 100 изделий, из которых 6 – бракованные. Партия произвольно разделена на две равные части, которые отправлены двум потребителям. Какова вероятность того, что все бракованные изделия достанутся одному потребителю?
51. Найти вероятность того, что из 10 книг, расположенных в случайном порядке, 3 определённые книги окажутся рядом?
52. На один ряд из семи мест случайным образом рассаживаются 7 учеников. Найти вероятность того, что три определённых ученика окажутся рядом?
53. Какова вероятность того, что при случайном расположении в ряд кубиков, на которых написаны буквы А, Г, И, Л, М, О, Р, Т получится слово алгоритм?
54. Лифт начинает движение с четырьмя пассажирами и останавливается на 10 этаже. Какова вероятность, что никакие два пассажира не выйдут на одном этаже.
55. Наудачу взятый телефонный номер состоит из 5 цифр. Какова вероятность того, что в нём все цифры: а) различные; б) одинаковые; в) нечётные? Известно, что номер телефона не начинается с цифры ноль.
56. Из 30 учащихся спортивной школы 12 человек занимаются баскетболом, 15 – волейболом, 5 – волейболом и баскетболом, а остальные – другими видами спорта. Какова вероятность того, что наудачу выбранный спортсмен занимается только волейболом или только баскетболом?
57. В магазине было продано 12 из 20 холодильников двух марок, имеющихся в количестве 9 и 11 штук. Полагая, что вероятность быть проданным для холодильника каждой марки одна и та же, найти вероятность того, что остались нераспроданными холодильники одной марки.
58. В лотереи 2 000 билетов; из них на 4 билета выпадают выигрыши по 2 500 рублей, на 10 билетов – по 1 000 рублей, на 20 билетов – по 500, на 5 билетов – по 100 рублей. Остальные билеты без выигрыша. Какова вероятность выиграть не менее 500 рублей, если куплен один билет?
59. В партии из 120 деталей отдел технического контроля обнаружил 6
13
нестандартных деталей. Чему равна относительная частота появления нестандартных деталей?
60. При испытании партии приборов относительная частота годных приборов оказалась равной 0,9. Найдите число годных приборов, если всего было проверено 200 приборов.
61. Два студента – А и В условились встретиться в определённом месте, договорились только о том, что каждый является туда в любой момент времени между 11 и 12 ч. и ждёт в течение 30 мин. Если партнёр к этому времени ещё не пришёл или уже успел покинуть установленное место, встреча не состоится. Найдите вероятность того, что встреча состоится.
62. Используя условие задачи 62, найдите вероятность того, что встреча состоится, если время ожидания не превысит 15 мин.
63. В течение 20 мин после девяти часов менеджер А в случайный момент времени звонит по телефону менеджеру В, ждёт 2 мин, после чего кладёт трубку. В течение тех же 20 мин менеджер В заходит в кабинет в случайный момент и остаётся в кабинете в течение 4 мин. Какова вероятность того, что разговор между менеджерами состоится?
1.3. Теоремы сложения и умножения вероятностей
Теорема сложения вероятностей несовместных событий. |
|
|
Вероятность появления одного из |
двух несовместных событий равна сумме |
|
вероятностей этих событий: Р(А В) |
Р(А) Р(В) . |
(1.9) |
Теорема сложения вероятностей |
совместных событий |
|
Вероятность появления хотя бы одного из двух несовместных событий |
||
равна сумме вероятностей этих событий без вероятности их совместного |
||
появления: Р(А В) Р(А) Р(В) Р(АВ) . |
(1.10) |
|
Следствие. Сумма вероятностей противоположных событий равна единице. Р( А) Р( А) 1.
Теорема умножения вероятностей
Вероятность совместного появления двух событий равна произведению
вероятности |
одного из |
этих событий |
на условную |
вероятность другого, |
|
вычисленную |
в |
предположении, |
что |
первое |
событие |
наступило: Р( АВ) Р( А)РА (В) . |
|
|
(1.11) |
||
Для независимых событий Р(АВ) Р(А)Р(В) . |
|
(1.12) |
|||

14
Пример 1.12. На станции отправления имеется 8 заказов на отправку товара: пять – в Хабаровский край, три – в Приморский край. Какова вероятность того, что два выбранных наугад заказа окажутся предназначенными для потребления в Хабаровском крае?
Решение. Событие А – первый взятый наугад заказ для Хабаровского края. Событие В – второй заказ так же предназначен для потребления в Хабаровском крае. Нам необходимо найти вероятность Р(АВ). Тогда по теореме об умножении вероятностей зависимых событий, используя формулу (1.11), имеем
Р( АВ) Р( А)Р (В) |
5 |
4 |
|
5 |
. |
|
|
|
|
|
|||
А |
8 |
7 |
14 |
|||
|
||||||
Пример 1.13. Из партии изделий товаровед наудачу отбирает изделия высшего сорта. Вероятность того, что выбранное изделие окажется высшего сорта, равна 0,8; первого сорта − 0,7; второго сорта − 0,5. Найти вероятность того, что из трёх наудачу отобранных изделий будут: а) только два высшего сорта; б) все разного сорта.
Решение. Пусть событие А1 – изделие высшего сорта; событие А2 – изделие первого сорта; событие А3 – изделие второго сорта. События А1,А2,А3 – независимы. По условию задачи Р(А1) = 0,8, Р(А2) = 0,7, Р(А3) = 0,5.
а) |
Событие А – только два изделия из трёх отобранных |
высшего сорта |
|||||||||||||
будет выглядеть так: А = А1А1А2+А1А1А3, |
|
|
|
|
|
||||||||||
Р( А) |
Р( А А А |
А А А ) |
Р( А )Р( А )Р( А ) |
Р( А )Р( А )Р( А ) |
(0,8)2 |
0,7 |
|||||||||
|
|
1 |
1 |
2 |
1 |
1 |
3 |
1 |
1 |
2 |
1 |
1 |
3 |
|
|
(0,8)2 0,5 |
0,768. |
|
|
|
|
|
|
|
|
|
|
|
|||
б) Событие В – все три изделия различного сорта, выразим так В |
А1 А2 А3 , |
||||||||||||||
тогда Р(В) |
0,8 |
0,7 |
0,5 |
0,28 . |
|
|
|
|
|
|
|
||||
Указания. Анализ и решение задач включённых в данный параграф, можно осуществлять по следующей схеме:
1.Уясните, в чём состоит рассматриваемое в задаче испытание.
2.Обозначьте буквами события, рассматриваемые в условии задачи.
3.С помощью введённых обозначений выразите событие, вероятность наступления которого необходимо найти.
4.Если требуется найти вероятность суммы событий, выясните, совместны или несовместны рассматриваемые события. Если же требуется найти вероятность произведения событий, выясните, зависимы или независимы рассматриваемые события.
15
5.Выберите соответствующую условию задачи формулу и выполните необходимые вычисления.
Задачи.
64. Укажите, какие из следующих пар событий являются несовместными:
а) наудачу выбранное натуральное число от 1 до 100 включительно: делится на 10; делится на 11;
б) нарушение в работе: первого; второго мотора летящего самолёта; в) попадание; промах при одном выстреле; г) выигрыш; проигрыш в шахматной партии;
д) наудачу выбранное натуральное число от 1 до 25 включительно является: чётным; кратным трём?
65. Брокерская фирма имеет дело с акциями и облигациями. Для анализа деятельности фирме полезно оценить вероятность того, что лицо, интересующее фирму, является держателем акций (событие А) или облигаций (событие В). Определите в этом контексте следующие события: а) клиент является держателем акций и облигаций; б) или держателем акций, или держателем облигаций, или акций и облигаций.
66. Среди студентов данной группы выбирают наудачу одного. Пусть событие А означает, что выбранный студент окажется юношей, событие В – студент-отличник, событие С – студент живёт в общежитии. Опишите событие АВ
67. Если событие А – выигрыш по билету одной лотереи, В – выигрыш по билету другой лотереи, то что означают события:
а) С= ; б) Д = А
; б) Д = А +
+  + АВ.
+ АВ.
68. Пусть А, В, С – три события. Записать выражения для событий, состоящих в том, что из А, В, С: а) все три события произошли; б) произошло только событие А; в) произошло А и В, а событие С не произошло; г) произошло только одно событие; д ) произошло только два события.
69. Вероятность для компании, занимающейся строительством, получить контракт в стране А, равна 0,4, в стране В – 0,3. Вероятность того, что контракты будут заключены и в стране А, и в В равна 0,12. Чему равна вероятность того, что компания получит контракт хотя бы в одной стране?
70. На предприятии работает 550 сотрудников, 380 из них имеют высшее образование, а 412 – среднее специальное образование, 357 сотрудников имеют
16
и высшее, и среднее специальное образование. Чему равна вероятность того, что случайно выбранный работник имеет либо среднее специальное, либо высшее образование, либо и то и другое?
71. Студент отвечает на 5 вопросов теста «да» и «нет». Какова вероятность того, что ответы на все вопросы оказались правильными, если он отвечал наудачу?
72. Коэффициенты использования рабочего времени у двух комбайнов соответственно равны 0,8 и 0,85. Считая, что остановки в работе каждого комбайна возникают случайно и независимо друг от друга, определить относительное время (вероятность): а) работы только одного комбайна; б) простоя обоих комбайнов.
73. Мастер обслуживает 4 станка, работающих независимо друг от друга. Вероятность того, что первый станок в течение смены потребует внимания рабочего 0,32, второй – 0,24, третий – 0,41, четвёртый – 0,25. Найти вероятность того, что в течение смены не потребуют внимания рабочего: а) один станок; б) 3 станка; в) 4 станка; г) хотя бы один станок.
74. Издательство направляет газеты в три почтовых отделения. Вероятность своевременной доставки газет в первое отделение равна 0,95, во второе отделение – 0,92 и в третье – 0,84. Найти вероятность того: а) что газеты получат вовремя только одно отделение; б) хотя бы одно отделение получит газеты с опозданием.
75. Вероятности своевременного возвращения кредита каждым из трёх заёмщиков банку независимы и соответственно равны: 0,76; 0,89; 0,97. Найти вероятность следующих событий: а) только два заёмщика возвратят кредит своевременно; б) хотя бы два заёмщика возвратят кредит своевременно.
76. Абонент разыскивает нужный номер телефона в трёх телефонных справочниках. Вероятность того, что формула содержится в первом, втором и третьем справочниках, равна соответственно 0,6; 0,9; 0,8. Найти вероятность того, что нужный номер содержится не менее чем в двух справочниках.
77. Контрольная работа состоит из 3 задач по алгебре и 3 задач по геометрии. Вероятность правильно решить задачу по алгебре равна 0,8, а по геометрии – 0,6. Какова вероятность правильно решить все три задачи хотя бы по одному из предметов?
78. На участке работают две бригады. Вероятность выполнения плана первой бригадой равна 0,9. Вероятность выполнения плана хотя бы одной бригадой
17
равна 0,995. Найти вероятность выполнения плана: а) второй бригадой; б) только одной бригадой.
79. Пакеты акций, имеющихся на рынке ценных бумаг, могут обеспечить доход своему владельцу с вероятностью 0,5 (для каждого пакета). Сколько пакетов акций различных фирм нужно приобрести, чтобы с вероятностью, не меньшей 0,968, можно было ожидать доход хотя бы по одному пакету акций?
80. На курсах повышения квалификации бухгалтеров преподаватель предлагает пакет из 10 накладных, 3 из которых содержат ошибки. Из пакета наудачу выбирают 6 накладных. Найти вероятность того, что среди извлечённых накладных: а) хотя бы одна с ошибками; б) хотя бы две с ошибками.
81. Рекламное агентство получило приглашение принять участие в конкурсе на выполнение работ от двух компаний. Вероятность получения заказа от фирмы А – 0,45. Если агентство заключит договор с компанией А, то вероятность получения заказа от компании В будет равна 0,9. С какой вероятностью компания получит оба заказа?
82. Вероятность получения фирмой кредита в банках №1, №2, №3 соответственно равны 0,4, 0,8, и 0,5. Для получения кредита было решено обратиться во второй банк, а в случае отказа – в третий и, наконец, в первый, если откажут в третьем. Какова вероятность получения кредита? Изменится ли вероятность получения кредита при другом порядке обращения?
83. |
На 100 лотерейных билетов приходится 5 выигрышных. Какова |
||
вероятность |
выигрыша хотя бы |
по одному билету, если приобретено: |
|
а) 2 билета; |
б) 4 билета. |
|
|
84. |
На |
связке 5 ключей. К замку подходит только один ключ. Найти |
|
вероятность |
того, что потребуется |
не более двух попыток открыть замок, если |
|
опробованный ключ в дальнейших испытаниях не участвует?
85. При включении зажигания двигатель начнёт работать с вероятностью 0,6. Найти вероятность того, что: а) двигатель начнёт работать при третьем включении зажигания; б) для запуска двигателя придётся включать зажигание не более трёх раз.
86. В данной местности среднее число дождливых дней в августе равно 10. Найти вероятность того, что в первые два дня августа не будет дождя?
87. В урне лежат 5 чёрных шаров, 4 красных и 3 белых шара. Последовательно извлекают 3 шара, причём каждый раз шар возвращается в урну перед тем, как извлечь следующий. Найти вероятность того, что первый
18
шар окажется чёрным, второй – красным, третий – белым. Как изменится вероятность этого события, если шар в урну не возвращается?
88. Работа электронного устройства прекратилась вследствие выхода из строя одного из пяти блоков. Производится последовательная замена каждого блока новым до тех пор, пока устройство не начнёт работать. Какова вероятность того, что придётся заменить: а) два блока; б) три блока.
89. Партия товара состоит из 40 костюмов четырёх размеров (по 10 костюмов каждого размера). Какова вероятность того, что четыре наугад взятых костюма будут разных размеров?
90. Студент знает 20 из 25 вопросов программы. Найти вероятность того, что студент из предложенных ему экзаменатором трёх вопросов знает: а) все три; б) два; в) не более одного.
91. Вероятность того, что выпускник финансового факультета защитит диплом на «отлично» , равна, 0,6. Вероятность того, что он защитит диплом на «отлично» и получит приглашение на работу в банк, равна 0,4. Предположим, что студент защитил диплом на «отлично». Найти вероятность того, что он получит приглашение на работу в банк.
92. Вероятность снижения процентной ставки кредитования более чем на 0,5 % в течение определённого периода равна 0,25. Вероятность увеличения объёма выпуска продукции при условии снижения процентной ставки кредитования более чем на 0,5 % за тот же период равна 0,72. Чему равна вероятность того, что процентная ставка кредитования снизится, а выпуск продукции увеличится.
93. Обследование 150 семей показало, что 90 семей имеют импортный телевизор, 60 – отечественный, 30 имеют отечественный и импортный телевизоры. Найти вероятность того, что: а) семья имеет отечественный и импортный телевизоры; б) если семья имеет импортный телевизор, то она имеет и отечественный.
94. Исследования, проводимые социологами, показали, что среди 250 опрошенных 160 – с высшим образованием, 180 – в возрасте до 30 лет, из них 126 – с высшим образованием. Найти вероятность того, что: а) опрошенный человек имеет высшее образование и моложе 30 лет; б) если опрошенный до 30 лет, то он имеет высшее образование.
95. Заведующий рекламным отделом журнала оценивает вероятность того, что подписчик прочтёт некоторую рекламу, как 0,4, а вероятность того, что он после этого купит рекламируемый товар, как 0,01.
19
а) Используя эти оценки, найти вероятность того, что подписчик прочтёт рекламу и купит рекламируемый товар.
б) Предположим, что вероятность прочтения рекламы лицом, не являющимся подписчиком журнала, равна 0,03, причём, если он это сделает, то вероятность покупки им рекламируемого товара равна 0,08. Какова вероятность того, что случайно выбранный человек прочтёт рекламу и купит товар?
1.4. Формула полной вероятности. Формула Байеса
Формула полной вероятности
Если событие А может произойти с одной из попарно несовместных гипотез Н1, Н2,….Нn, образующих полную группу, то вероятность появления события А равна сумме произведений вероятностей каждой из гипотез на соответствующую условную вероятность события А:
Р(А) Р(Н1)РН1 (А) Р(Н2 )РН 2 (А) ... Р(Нn )PH n (A) , |
(1.13) |
n
где P(Hi ) 1 .
i 1
Формула Байеса
Формула Байеса определяет условную вероятность появления гипотезы Hi, при условии, что событие А уже произошло:
PA |
H i |
P(H i ) PHi ( A) |
|
P(H i ) |
PHi |
( A) |
. |
(1.14) |
P( A) |
|
n |
|
|
||||
|
|
|
P(H i ) |
PHi ( A) |
|
|
||
|
|
|
|
|
|
|||
|
|
|
|
i 1 |
|
|
|
|
Пример 1. 14. Фирма имеет три источника поставки комплектующих – фирмы А, В, С. На долю фирмы А приходится 50% общего объёма поставок, В – 30% и С-20%. Из практики известно, что 10% деталей, поставляемых фирмой А – бракованные, фирмой В – 5% и С − 6%. Найти вероятность того, что наудачу выбранная деталь будет бракованной.
Решение: Производится испытание: извлекается одна деталь. Событие А – извлечённая деталь бракованная .
Гипотеза Н1 – деталь фирмы А; гипотеза Н2 – деталь фирмы В; гипотеза Н3 – деталь фирмы С.
Согласно формуле полной вероятности (1.13), искомая вероятность равна:
Р(А) Р(Н1)РН1 (А) Р(Н2 )РН 2 (А) Р(Н3 )PН3 (A) .

20
Из условия задачи: |
Р(Н1) |
0,5 ; Р(Н2 ) |
0,3 ; Р(Н3 ) 0,2 . |
||||
РН1 (А) |
0,1 ; PH 2 |
( A) |
0,05 ; |
PH3 |
( A) |
0,06 . |
|
Р(А) = |
0,5 0,1 |
+ 0,3 0,05 |
+ |
0,2 |
0,06 |
= 0,077. |
|
Пример 1.15. |
В центральную бухгалтерию корпорации поступили пачки |
||||||
накладных для проверки и обработки. 90% пачек были признаны удовлетворительными: они содержали только 1% неправильно заполненных накладных. Остальные 10% пачек были признаны неудовлетворительными, так как содержали 5% неверно оформленных накладных. Взятая наугад из пачки накладная оказалась оформленной неверно, какова вероятность того, что пачка
накладных, |
из которой изъята накладная признана неудовлетворительной ? |
||||||||
Решение: Испытание: |
проверяется пачка накладных. |
||||||||
Событие А − взятая наугад накладная оказалась неверно оформленной. |
|||||||||
Гипотеза Н1 − пачка не соответствует стандарту. |
|||||||||
Гипотеза Н2 |
− пачка соответствует стандарту. |
||||||||
Необходимо найти |
вероятность гипотезы Н1 при условии, что событие А |
||||||||
произошло. Согласно формуле Байеса (1.14) |
имеем: |
||||||||
PA H1 |
|
|
P(H1 ) |
|
PH ( A) |
; |
|
||
|
|
|
|
1 |
|
||||
|
|
|
|
|
|
|
|
||
|
P(H1 ) |
PH ( А ) |
|
P(H2 ) PH |
( A) |
|
|||
|
|
|
1 |
|
|
|
2 |
|
|
Р(Н1) 0,1; |
Р(Н2 ) 0,9 ; |
РН1 ( А) 0,05 PH 2 ( A) |
0,01; |
||||||
PA H1 |
|
0,1 |
0,05 |
|
|
0,357. |
|
|
|
|
|
|
|
|
|
|
|
||
0,1 |
0,05 |
0,9 |
|
|
|
|
|
||
|
0,01 |
|
|
|
|||||
Задачи
96.На складе хранится 10 изделий компании А, 15 изделий компании В и 30 изделий компании С. Вероятность того, что А производит изделия высшего сорта, равна 0,9, В – 0,8 и С − 0,7. Найдите вероятность того, что случайно выбранное изделие окажется высшего сорта.
97.Вероятности обращения фирмы за кредитом в один из четырёх банков соответственно равны р1 = 0,3, р2 = 0,2, р3 = 0,4 и р4 = 0,1. Вероятность отказа в кредите в первом банке равна 0,4, во втором − 0,5, в третьем и четвёртом банках эти вероятности соответственно равны 0,2 и 0,7. Найдите вероятность того, что фирма получит кредит после обращения в наугад взятый банк.
98.Из имеющегося набора карточек с буквами, составляющими слово "экономика", наугад взяли две карточки, после чего случайным образом взяли ещё одну. Какова вероятность того, что карточка будет с гласной буквой?
21
99.В торговую фирму поступили телевизоры от трёх поставщиков в отношении 1:4:5. Практика показала, что телевизоры, поступающие от 1-го, 2-го, и 3-го поставщиков, не потребуют ремонта в течение гарантийного срока соответственно в 98%, 88% и 92% случаев. Найдите вероятность того, что поступивший в продажу телевизор не потребует ремонта в течение гарантийного срока.
100.Для изготовления продукции используются детали четырёх заводов. Первый завод поставил 2 000 деталей, второй − 1 700, третий − 200 и
четвёртый поставил 2 000. Известно, что процент бракованных деталей среди продукции первого завода составляет 0,2%, второго − 0,3%, третьего − 0,2% и четвёртого − 0,5%. Какова вероятность того, что наугад взятая деталь окажется бракованной?
101.В вычислительной лаборатории имеется 6 персональных компьютеров одного типа и 4 другого. Вероятность того, что за время работы компьютер первого типа не выйдет из строя, равна 0,999, а для компьютеров второго типа эта вероятность равна 0,99. Студент сел выполнять работу за наугад выбранный компьютер. Найдите вероятность того, что до окончания работы компьютер не выйдет из строя.
102.Электрические лампочки изготавливаются на трёх заводах. Первый из этих заводов поставляет 40% общего количества, второй − 35% и третий − 25%. Продукция первого завода содержит 80% стандартных ламп, второго − 90%, третьего − 98%. Все изготовленные лампочки поступают в магазин. а) Какова вероятность того, что купленная в магазине лампочка окажется стандартной? б) Купленная лампочка оказалась стандартной. Найти вероятность того, что она изготовлена на первом заводе.
103. Страховая компания разделяет застрахованных по классам риска: I класс – малый риск, II – класс средний, III класс – большой риск. Среди клиентов компании 50% − первого класса риска, 30% − второго и 20% − третьего. Вероятность выплаты страхового вознаграждения для клиента первого класса риска 0,01, для второго – 0,03, для третьего – 0,08. а) Какова вероятность того, что застрахованный клиент получит денежное вознаграждение за период страхования. б) купленная лампочка. б) Застрахованный клиент получил страховое вознаграждение. Найти вероятность того, что он относится к III классу риска.
104. В специализированную больницу поступают в среднем 55% больных с заболеванием А, 25% − с заболеванием В, 20% − с заболеванием С. Вероятность
22
полного излечения болезни А равна 0,7, для болезней В и С эти вероятности соответственно равны 0,8 и 0,9. Больной, поступивший в больницу, был выписан здоровым. Найдите вероятность того, что этот больной страдал заболеванием С.
105.Два бухгалтера обрабатывают равное количество счетов. Вероятность того, что первый бухгалтер допустит ошибку, равна 0,005, для второго эта вероятность равна 0,01. При проверке счетов была найдена ошибка. Найдите вероятность того, что её допустил первый бухгалтер.
106.Имеется три группы студентов. В первой группе 24 человека, во второй − 26 и в третьей − 20. Экзамен по теории вероятностей сдали на «отлично» в первой группе 6 человек, во второй − 7 и в третьей группе − 4 студента. На общем собрании студентов этих групп выбирают случайным образом одного студента. Какова вероятность того, что выберут студента первой группы, сдавшего экзамен по теории вероятностей на «отлично»?
107.Коллектив академии избирает ректора. Среди избирателей 30% − преподаватели, 60% − студенты и 10% − прочий персонал. Вероятность того, что преподаватель проголосует за определённого кандидата, равна 0,7, среди остальных избирателей эта вероятность равна 0,5. Найдите вероятность того, что кандидат будет избран (кандидат считается избранным, если за него проголосовало более 50% избирателей).
108.Число грузовых автомашин, проезжающих по шоссе, на котором стоит автозаправочная станция, относится к числу легковых машин как 2:3. Вероятность того, что проезжающая грузовая машина будет заправляться, равна 0,1, для легковой машины эта вероятность равна 0,2. К автозаправочной станции подъехала для заправки машина. Найдите вероятность того, что это грузовая машина.
109.Два охотника стреляют одинаковыми пулями в медведя. В результате медведь был убит одной пулей (событие А). Как охотники должны поделить шкуру убитого медведя, если известно, что вероятность попадания у первого охотника 0,3, а у второго – 0,6?
110.Уголь закупается у двух поставщиков А и В. Если в течение четырёх дней уголь не поступает, то производственный процесс останавливается. Вероятность того, что уголь поступит в 4 дня от А равна 0,6, от В – 0,35. Производственный процесс не был остановлен в 4 дня. Найти вероятность того, что уголь поступил от поставщика В.

23
111.Некто, заблудившись в лесу, вышел на поляну, откуда вели 4 дороги. Известно, что вероятности выхода из леса за час для различных дорог равны соответственно 0,6; 0,3; 0,2; 0,1. Чему равна вероятность того, что заблудившийся пошёл по первой дороге, если известно, что через час он вышел из леса?
112.На Дальнем Востоке 70% совместных предприятий занимаются экспортно-импортной деятельностью, остальные 30% – производители. В конце года 10% первых и 4% вторых не предоставили деклараций в налоговую инспекцию. Найти вероятность того, что: а) предприятие является компаниейпроизводителем, если оно нарушило законодательство; б) найти вероятность того, что случайно выбранное предприятие является законопослушным.
113.Экономист полагает, что в течение периода активного экономического роста американский доллар будет расти в цене с вероятностью 0,7, в период умеренного экономического роста он подорожает с вероятностью 0,4 и при
низких темпах роста – с вероятностью 0,2. Вероятность активного экономического роста в стране оценивается аналитиками как 0,3; умеренного экономического роста – 0,5 и низкого роста 0,2. Предположим, что доллар дорожает в течение текущего периода. Чему равна вероятность того, что анализируемый период совпал с периодом активного экономического роста?
114. Из числа авиалиний некоторого аэропорта 60% – местные, 30%– по странам СНГ и 10% – в страны дальнего зарубежья. Среди пассажиров местных авиалиний 50% путешествуют по делам, связанным с бизнесом, на линиях СНГ – 60%, на международных – 90%. Из прибывших в аэропорт пассажиров случайно выбирается один. Чему равна вероятность того, что он: а) бизнесмен; б) прибыл из стран СНГ по делам бизнеса; в) прибыл местным рейсом по делам бизнеса; г) прибывший международным рейсом бизнесмен.
115*. Задача о разорении1. Петя с папой играют в следующую игру. Петя бросает монету, предварительно сообщив папе, какая сторона, по его мнению, выпадет: «герб» или «решка». Если Петя угадал, то папа платит Пете 1 руб., в противном случае Петя платит папе рубль. Начальный капитал Пети составляет х = 100 руб. Игра продолжается до тех пор, пока Петя не наберёт заранее определённую сумму s, либо пока он не разорится, проиграв весь имеющийся
1 Практическая интерпретация задачи состоит в следующем. Инвестиционная компания «играет» с рынком. Возможности рынка неограниченны. Компания пытается угадать, какие финансовые инструменты окажутся в будущем доходными, если угадывает – получает прибыль, иначе – несёт убытки. Если убытков становится много, то рано или поздно компания разоряется.
24
капитал x. Найти вероятность того, что Петя разорится, так и не набрав желаемую сумму, если эта сумма s составляет:
а) 110 руб.; б) 1 000 руб.
116*. Задача о разборчивой невесте2. У одной из Машиных подруг есть достаточно большое число женихов. Заранее она о своих женихах ничего не знает, кроме их числа n. Расположившись в очередь в случайном порядке, женихи представляются разборчивой невесте один за другим так, что встречая очередного жениха, она знает всех предыдущих. Представленный и отвергнутый жених больше не возвращается. Невеста решила избрать следующую стратегию выбора: она просматривает первых m женихов, никого из них не выбирая, а затем останавливает свой выбор на первом из оставшихся (n – m) женихов, который окажется лучше, чем любой из первых m женихов. Найти вероятность Pm(A) сделать наилучший выбор при такой стратегии. Определить такое число m*, чтобы вероятность Pm* (A) была максимальной среди всех Pm(A), m=0,1… ,n.
1.5. Повторные независимые испытания
Формула Бернулли
Вероятность того, что в n независимых испытаниях, в каждом из которых
вероятность появления события А постоянна и равна |
p и не равна 0 и 1, |
|
событие А наступит ровно m раз, вычисляется по формуле Бернулли: |
||
Р (m) |
Cm pmqn m , где q 1 p . |
(1.15) |
n |
n |
|
Локальная теорема Лапласа
При большом числе испытаний для решения подобных задач применяется формула
Рn (m) |
|
1 |
|
|
|
|
(x) , |
(1.16) |
|||||||
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|||||||||||
npq |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
1 |
|
|
|
x 2 |
|
m |
np |
|
|
||||
где (x) |
|
|
e 2 и x |
|
. |
||||||||||
|
|
|
|
|
|
|
|
|
|||||||
|
|
2 |
|
|
|
|
|
|
npq |
||||||
2 Финансовая формулировка данной задачи: пусть инвестор владеет некоторым активом, причем в течение определённого срока цена актива может изменяться, а по окончании срока – станет фиксированной (таким активом может быть облигация, рыночная котировка которой может изменяться до момента погашения, или какой-либо инвестиционный проект, пока он не завершён). Стоимости актива в предыдущие дни известны, а в последующие – нет. К предыдущему дню вернуться уже нельзя. Требуется определить момент продажи актива с наибольшей выгодой.
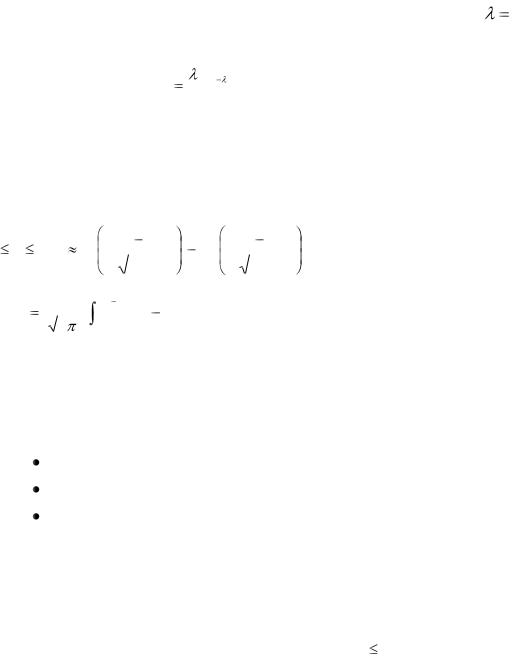
25
Функция φ (х) – чётная, т.е. φ(-х) = φ (х). Функция φ (х) табулированная на отрезке [0; 4], поэтому для х ≥ 4 функция φ (х) ≈ 0.
В приложении А приведена таблица значений этой функции.
Теорема Пуассона |
|
|
|
|
||
Если |
вероятность |
р |
наступления |
события А в каждом испытании |
||
стремится |
к |
0 ( р →0) при |
неограниченном увеличении числа испытаний |
|||
( n →∞), причем произведение |
np стремится к постоянному числу |
np , то |
||||
вероятность |
Pn (m) того, |
что |
событие А из |
n испытаний наступит |
m раз |
|
|
m |
|
|
находится по формуле Pn (m) |
|
e . |
(1.17) |
|
|||
|
m! |
|
|
В приложении В приведена таблица значений этой функции.
Интегральная теорема Лапласа
вероятность того, что событие наступает не менее |
m1 раз и не более m2 раз |
||||||||
приближенно равна |
|
|
|
|
|
|
|
|
|
P (m1 m m2 ) Ф |
m2 |
n p |
Ф |
m1 |
n p |
, |
(1.18) |
||
|
|
|
|
|
|
||||
|
n p q |
|
n p q |
||||||
|
|
|
|
|
|
||||
где Ф (x) |
|
1 |
|
|
|
|
|
|
|
|
|
2 |
|
||
|
|
|
x |
t 2 |
|
|
e |
2 dt |
функция Лапласа. |
|
0 |
|
|
|
Ф(х) нечётная, т.е. Ф(-х) = Ф(х), для х > 5 Ф(х) ≈ 0,5.
В приложении Б приведена таблица значений функции Лапласа.
Формулы Бернулли, Лапласа и Пуассона применяются в тех случаях, когда рассматриваются испытания , удовлетворяющие схеме Бернулли, т.е.
проводимые испытания независимы;
каждое испытание имеет только два исхода;
вероятность появления события в каждом испытании постоянна и равна р .
При этом важно правильно выбрать соответствующую формулу: (1.15),
(1.16), (1.17), (1.18).
Указания. При выборе формулы можно руководствоваться следующим:
1.Если число независимых испытаний n 10, то для вычисления вероятности появления события m раз пользуются формулой Бернулли (1.15).
26
2. Если число независимых испытаний n |
10 и требуется найти |
|
вероятность появления события от m1 |
до m2 раз, то используется |
|
|
m2 |
|
формула Pn (m1 m m2 ) |
Pn (m) . |
|
|
m1 |
|
3.Если число независимых испытаний n достаточно велико, а вероятность появления события в каждом испытании мала (стремится к 0) и  np 10, то для вычисления вероятности Pn (m)
np 10, то для вычисления вероятности Pn (m)
применяют формулу Пуассона (1.17).
4.Если число независимых испытаний n достаточно велико,
вероятность появления события в каждом испытании |
отлична от |
||
0 и 1, то для вычисления |
Pn (m) применяют формулу |
(1.16). |
|
5. Если число независимых испытаний n |
достаточно велико, то для |
||
вычисления вероятности |
появления события от m1 до m2 раз: |
||
|
|
m2 |
|
а) при малом числе слагаемых в сумме |
Pn (mi ) можно применять |
||
|
|
m1 |
|
локальную формулу Лапласа, т.е.
|
|
|
|
|
m2 |
1 |
|
m2 |
|
mi |
np |
|
|
|
|||
P (m |
m |
m ) |
|
P (m) |
|
|
|
( |
) ; |
|
( 1.19) |
||||||
|
|
|
|
|
|
|
|
|
|
||||||||
n |
1 |
|
2 |
|
n |
npq m1 |
|
|
|
npq |
|
|
|||||
|
|
|
|
|
m1 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m2 |
|
|
б) |
при |
малом |
числе слагаемых |
в сумме |
Pn (mi ) и |
малой |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m1 |
|
|
вероятности |
появления |
события |
в каждом |
испытании, |
при |
||||||||||||
|
np |
10 применяют формулу Пуассона, т.е. |
|
|
|||||||||||||
|
|
|
|
|
m2 |
|
|
m2 |
mi |
|
|
|
|
|
|||
|
Pn (m1 |
m |
m2 ) |
Pn (mi ) |
e |
|
|
|
|
|
; |
|
|
|
(1.20) |
||
|
|
|
mi! |
|
|
|
|||||||||||
|
|
|
|
|
m1 |
|
|
m1 |
|
|
|
|
|
||||
в) при достаточно большом числе слагаемых применяется интегральная теорема Лапласа.
Наивероятнейшее число появления события
Если n – число независимых испытаний, р – вероятность наступления события А в отдельном испытании, то наивероятнейшее число m0 появления события А удовлетворяет неравенству np – q ≤ m0 ≤ np + p.
Следствие интегральной теоремы Лапласа
Если вероятность |
p |
наступления события А в каждом из n |
|
независимых испытаний |
постоянна и |
отлична от 0 и 1, то при достаточно |
|
большом числе испытаний вероятность |
того , что |
||

27
|
а) число m наступлений события А отличается от произведения np не более |
||||||||||||||||||||||||||||||
чем |
на |
величину |
ɛ |
|
> |
0 |
(по |
абсолютной |
величине), |
|
т. е. |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P( |
m |
np |
|
) |
2Ф |
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
npq |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
б) частость |
|
|
события А |
отличается от его вероятности |
р не более чем на |
|||||||||||||||||||||||||
|
n |
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
величину |
> 0 ( по абсолютной величине ), т.е. |
P( |
m |
p |
|
) |
2Ф |
|
|
n |
|
|
|||||||||||||||||||
n |
|
|
|
|
|
|
|||||||||||||||||||||||||
|
pq . |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
Пример 1.16. Вероятность выигрыша по одному любому лотерейному |
||||||||||||||||||||||||||||||
билету равна 0,02. Чему равна вероятность выигрыша для владельца |
|
|
|
четырёх |
|||||||||||||||||||||||||||
билетов |
|
а) по трём |
билетам; |
б) |
не |
более |
чем |
по двум |
|
|
билетам. |
||||||||||||||||||||
Решение: |
n = 4; |
p = 0,02 ; |
q = 0,98. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
а) |
Р (3) |
C 3 |
0,023 0,984 |
3 |
3 10 5 ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
4 |
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б) |
Р (0 |
m |
2) |
|
|
P (0) |
P (1) |
P (2) |
C 0 0,020 |
0,984 |
C1 0.021 |
0,983 |
|
|
|
|
|
||||||||||||||
|
|
4 |
|
|
|
|
|
4 |
|
|
|
4 |
|
|
4 |
4 |
|
|
|
|
4 |
|
|
|
|
|
|
|
|
||
C42 |
0,022 |
0,982 |
|
0,099. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
Пример |
1.17. |
|
|
Магазин |
получил |
1000 |
бутылок |
минеральной воды. |
||||||||||||||||||||||
Вероятность того, что при перевозке бутылка окажется разбитой, равна 0,003. Найти вероятность того, что магазин получит разбитых бутылок: а) ровно две;
б) меньше двух; |
в) больше одной; г) хотя бы одну. |
|
|
|
|
||||||||||||
|
Решение: |
|
|
|
Число независимых испытаний n =1000 достаточно велико, а |
||||||||||||
вероятность |
|
появления |
события |
в каждом |
испытании |
р 0,003 |
мала |
||||||||||
(стремится к 0 |
) |
и |
np |
3 10 , |
искомую вероятность будем находить по |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
формуле Пуассона (1.17), используя таблицу значений функции Pn (m, |
) |
|
e |
||||||||||||||
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m! |
|
(приложение В). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
а) P1000 (2) |
32 |
e 3 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
0,224 |
; |
|
|
|
|
|
|
|
|
|
|||
|
2! |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
б) |
|
|
|
|
|
|
|
|
|
30 e 3 |
3 e 3 |
|
|
|
|
||
P1000 (m |
2) |
|
P1000 (0) |
P1000 (1) |
|
|
|
|
0,0498 |
0,1494 |
0,1992; |
||||||
|
0! |
|
1! |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
в) |
P1000 (m 1) |
|
1 |
|
P(m 1) 1 |
(P1000 (0) |
|
P1000 (1)) |
0,8008; |
|
|
|
|
||||
г) |
P1000 (m 1) |
|
1 |
P1000 (0) |
1 |
0,0498 0,9502. . |
|
|
|
|
|
|
|
||||
Пример 1.18. Доля изделий высшего сорта на данном предприятии составляет 90%. Найти вероятность того, что из взятых на проверку 600
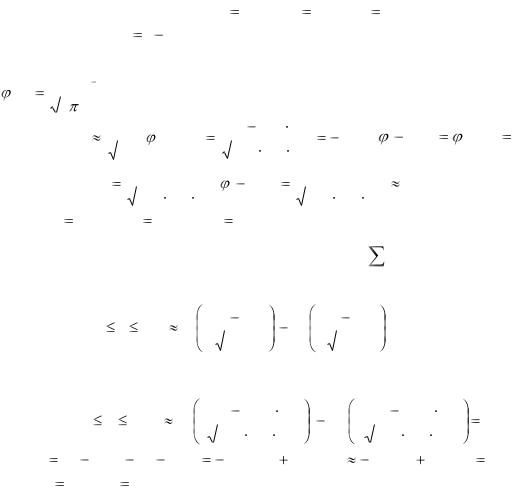
28
изделий: а) высшего сорта окажется 530 изделия; б) из 600 изделий от 520 до 535 изделий (включительно) будут высшего сорта; в) наивероятнейшее число изделий высшего сорта.
Решение. Эксперимент заключается в проведении 600 повторных независимых испытаний с двумя исходами в каждом. Вероятность появления изделия высшего сорта в каждом испытании постоянна. Следовательно, схема Бернулли применима.
а) По условию задачи |
|
|
|
|
n |
600, |
m |
530, |
p |
0,9 . |
Так как |
n |
достаточно |
||||||||||||||||||||||||||||||||||||||
велико, |
а |
|
p и |
q |
1 |
p не малы, то для вычисления |
искомой |
вероятности |
|||||||||||||||||||||||||||||||||||||||||||
применим |
|
локальную теорему Лапласа (1.16) |
|
и таблицу значений функции |
|||||||||||||||||||||||||||||||||||||||||||||||
|
1 |
|
|
x 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
(x) |
|
e 2 |
|
|
|
|
|
(приложение А) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
Рn |
(m) |
|
|
1 |
|
|
|
(x) , x |
530 |
600 0,9 |
|
|
1,36 |
; ( |
1,36) |
(1,36) |
0,1582; |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
npq |
|
|
600 0,9 0,1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
P600 (530) |
|
|
|
|
|
|
1 |
|
|
|
|
( |
1,36) |
|
|
|
|
|
|
0,1582 |
|
|
|
|
|
|
0,021; |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
600 |
0,9 |
0,1 |
600 |
0,9 |
0,1 |
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
б) |
|
n |
600, |
|
m1 520, |
|
m2 |
535. |
Так |
|
как |
число |
независимых |
испытаний |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m2 |
|
|
|
|
|
|
|
||||
достаточно велико и число слагаемых в сумме |
|
|
|
|
|
Pn (mi ) равно шестнадцати, то |
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m1 |
|
|
|
|
|
|
|
||||
для вычисления искомой |
|
|
вероятности воспользуемся интегральной теоремой |
||||||||||||||||||||||||||||||||||||||||||||||||
Лапласа |
P (m1 |
m |
|
m2 ) |
Ф |
|
|
m2 |
|
n p |
Ф |
|
m1 |
|
n p |
. |
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
n p q |
|
|
n p q |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Значения функции Лапласа, учитывая её нечётность, |
находим по таблице |
||||||||||||||||||||||||||||||||||||||||||||||||||
(приложение Б) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
P (520 m |
|
|
535) |
Ф |
535 |
|
600 0,9 |
|
|
|
|
Ф |
520 |
|
|
600 0,9 |
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
600 |
0,9 |
0,1 |
|
|
|
|
|
|
600 |
0,9 |
|
0,1 |
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
Ф( |
0,68) |
|
|
Ф( |
2,72) |
|
|
|
|
|
Ф(0,68) |
Ф(2,72) |
|
0,2517 |
0,4967 |
0,245 ; |
||||||||||||||||||||||||||||||||
в) |
n |
600, p |
|
|
0,9 q=0,1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
Наивероятнейшее число изделий высшего сорта определим по формуле np – q ≤ m0 ≤ np + p;
600·0,9 – 0,1 ≤ m0 ≤ 600·0,9 + 0,9; 539,9 ≤ m0 ≤ 540,9; m0=540.
Задачи
117.Вероятность того, что торговая база не превысит дневную норму расходов, равна 0,9. Определите вероятность того, что за пять дней норма дневных расходов будет превышена дважды.
118.Вероятность того, что посетитель магазина совершит покупку, равна 0,6. Найдите вероятность того, что из 8 посетителей покупку сделают:
а) не более двух человек; б) не менее двух человек.
29
119.Система состоит из шести независимо работающих элементов. Вероятность отказа элементов равна 0,3. Найдите: а) наивероятнейшее число отказавших элементов; б) вероятность наивероятнейшего числа отказавших элементов системы; в) вероятность отказа системы, если для этого достаточно, чтобы отказали, хотя бы пять элементов.
120.Тест по экономике состоит из 10 вопросов. На каждый вопрос в тесте
предлагается 4 варианта ответа, из которых нужно выбрать один правильный. Какова вероятность того, что, будучи совершенно не готовым к тесту, студент угадает правильные ответы, по крайней мере, на 6 вопросов?
121. Два равносильных противника играют в шахматы. Что вероятнее: а) выиграть одну партию из двух или две партии из четырёх; б) выиграть не менее двух партий из четырёх или не менее трёх партий из пяти (ничьи во внимание не принимаются)?
122.Вероятность хотя бы одного попадания при двух выстрелах равна 0,96. Найдите вероятность трёх попаданий при четырёх выстрелах.
123.Сколько раз следует двукратно подбросить монету, чтобы с вероятностью не менее 0,95 хотя бы один раз появилось событие «один герб и одна решка»?
124.Игральная кость брошена 9 раз. Найдите наивероятнейшее число очков, кратное трём, и вычислите его вероятность.
125.Сколько раз нужно бросить игральную кость, чтобы наивероятнейшее число появлений чётного числа очков было равно 6?
126.Аудиторную работу по теории вероятностей с первого раза успешно выполняют 60% студентов. Найдите вероятность того, что из 400 студентов работу успешно выполнят 265 студентов.
127.По результатам проверок налоговыми инспекциями установлено, что в среднем каждое третье малое предприятие региона имеет нарушение финансовой дисциплины. Найдите вероятность того, что из 1200 зарегистрированных в регионе малых предприятий имеют нарушения финансовой дисциплины: а) 410 предприятий; б) наивероятнейшее число таких предприятий.
128.Производители калькуляторов знают из опыта, что 2% проданных калькуляторов имеют дефекты. Аудиторская фирма купила 500 калькуляторов. Какова вероятность того, что придётся заменить: а) 4 калькулятора; б) не менее трёх калькуляторов?

30
129.Вероятность производства стандартной детали в некоторых условиях равна 0,97. Найдите наивероятнейшее число стандартных среди 625 деталей и вероятность такого числа деталей.
130.Сборник задач содержит 400 задач с ответами. В каждом ответе может быть ошибка с вероятностью 0,01. Какова вероятность, что 98% всех ответов на задачи сборника приведены без ошибок?
131.Вероятность того, что пассажир опоздает к отправлению поезда, равна 0,012. Найдите наиболее вероятное число опоздавших из 900 пассажиров и вероятность такого числа опоздавших.
132.Учебник издан тиражом 2 000 экземпляров. Вероятность того, что экземпляр учебника сброшюрован неправильно, равна 0,003. Найдите вероятность того, что: а) тираж содержит 5 бракованных книг; б) не более 3.
133. Вероятность того, что случайно выбранный лицевой счёт клиента отделения сбербанка содержит ошибки, равна 0,002. Если при выборочной проверке счетов обнаружится, что не менее 0,4% отобранных счетов содержат ошибки, то оператор увольняется с работы. Найдите вероятность того, что оператор будет уволен, если ревизор проверит 400 счетов.
135. Имеется общество из 730 человек. Найти: а) вероятность того, что у трёх человек день рождения приходится на Новый год; б) наиболее вероятное число человек, имеющих один и тот же день рождения и вероятность такого события.
Считать, что вероятность рождения в фиксированный день равна 3651 .
136. В новом микрорайоне поставлено 10 000 кодовых замков на входных дверях домов. Вероятность выхода из строя одного замка в течение месяца равна 0,000 4. Найдите вероятность того, что за месяц: а) откажут пять замков; б) откажут по крайней мере 3 замка; в) будут исправно работать 9 997 замков; г) будут исправно работать хотя бы 9 997 замков.
137.Завод отправил на базу 15 000 стандартных изделий. Среднее число изделий, повреждаемых при транспортировке, составляет 0,06%. Найдите вероятность того, что из 15 000 изделий будет повреждено от двух до пяти изделий.
138.Магазин произвёл 50 распродаж по сниженным ценам. Вероятность того, что каждая из них оправдала себя по окупаемости, составляет 0,08. Найдите вероятность, что хотя бы одна из распродаж оказалась неубыточной.
31
139.Каждый из 100 компьютеров в интернет-кафе занят клиентом в среднем
втечение 80% рабочего времени. Какова вероятность того, что в момент проверки клиентом будет занято: а) от 75 до 90 компьютеров; б) не менее 80 компьютеров; в) не более 74 ?
140.На научную конференцию приглашены 130 человек, причём каждый из них прибывает с вероятностью 0,7. В гостинице для участников конференции заказано 95 мест. Какова вероятность, что все приезжающие будут поселены в гостинице?
141.Страховая фирма заключила 10 000 договоров. Вероятность страхового случая по каждому в течение года составляет 2%. Найдите вероятность того, что таких случаев будет не более 250.
142.При обследовании уставных фондов банков установлено, что пятая часть банков имеет уставный фонд свыше 100 млн руб. Найдите вероятность того, что среди 1 800 банков имеют уставный фонд свыше 100 млн руб. от 330 до 400 включительно.
143.Инвестор решил вложить поровну средства в три предприятия при условии возврата ему через определённый срок 150% от вложенной суммы каждым предприятием. Найдите вероятность того, что по истечении срока кредитования инвестор получит обратно, по крайней мере, вложенную сумму, если вероятность банкротства каждого из предприятий равна 0,2.
144.Страховая компания застраховала 1 000 клиентов одного возраста и одной социальной группы. Вероятность смерти клиента в течение года – 0,006. Каждый клиент вносит 1 января 15 долларов. В случае смерти застрахованного лица наследникам выплачивается 1 200 долларов. Чему равна вероятность того, что: а) страховая компания разорится; б) получит более 10 000 долларов прибыли?
145.У страховой компании имеются 10 000 клиентов. Каждый из них, страхуясь от несчастного случая, вносит 500 руб. Вероятность несчастного случая 0,0055, страховая сумма, выплачиваемая пострадавшему, составляет 50 000 руб. Какова вероятность того, что: а) страховая компания потерпит убыток; б) на выплату страховых сумм уйдёт более половины всех средств, поступивших от клиентов; в) на какую прибыль может рассчитывать страховая компания с надёжностью 0,95.
146.В тесто, приготовленное для выпечки 1 000 булочек, засыпают 10 000 изюминок и тщательно перемешивают. Какова вероятность того, что в случайно
32
выбранной булочке будет: а) 5 изюминок; б) меньше 10 изюминок.
147.Мастер и ученик участвуют в шахматном матче. Мастер выигрывает матч, если он выиграл все партии в матче. Ученик выигрывает матч, если он выиграл хотя бы одну партию в матче. Из скольких партий должен состоять матч, чтобы шансы на победу у мастера и ученика были равны, если вероятность победы мастера в одной партии 0,9, а ученика – 0,1?
148.Статистическая вероятность рождения мальчика равна 0,515. Определите вероятность того, что среди 400 новорожденных доля мальчиков будет отличаться от вероятности рождения мальчика по абсолютной величине не
более чем: а) на 0,005; б) 0,01; в) 0,04. Как влияет величина допустимого отклонения на значение искомой вероятности?
149.При установившемся технологическом процессе вероятность изготовления бракованного шарика для шарикоподшипника равна 0,15. Определите вероятность того, что доля бракованных шариков среди изготовленных 1 000 шт. будет отличаться от вероятности изготовления бракованного шарика не более чем на 0,003 в ту или иную сторону. Как изменится результат, если шариков 625 шт.? Как влияет число отбираемых шариков на величину искомой вероятности?
150.Французский учёный Бюффон в 1777г. бросил монету 4 040 раз,
причём «герб» появился 2 048 раз. Найти вероятность того, что при повторении опыта Бюффона относительная частота появления «герба» отклонится от вероятности появления «герба» по абсолютной величине не более чем в опыте Бюффона.
151.Вероятность попадания в цель при каждом выстреле постоянна и равна 0,8. Найдите число выстрелов, необходимых для того, чтобы с вероятностью 0,954 4 относительная частота попаданий в цель отличалась от вероятности 0,8 по абсолютной величине не более чем на 0,01.
152.90% семян всходят. Найдите наименьшее отклонение (по абсолютной
величине) частости взошедших семян из 2 000 посеянных от вероятности 0,9, которое можно ожидать с вероятностью 0,990 7.
153.Найдите границы, в которых с вероятностью 0,861 2 находится относительная частота родившихся девочек из 2 500 новорождённых. Вероятность рождения девочки принять равной 0,485.
154.Для определения нормы высева требуется определить всхожесть семян с точностью до 0,01 и надёжностью 0,956 6. 80% семян всходят после посева, сколько семян следует проверить?
33
155.Среди проверенных наудачу отобранных 2 500 изделий из массовой продукции цеха оказалось 300 шт. бракованных. Определить вероятность того, что отклонение эмпирически установленной доли брака от доли брака во всей продукции цеха не превысит по абсолютной величине 0,01. Указание: доля брака во всей продукции цеха принимается равной вероятности того, что наудачу взятое изделие из всей продукции окажется бракованным.
156.Вероятность изготовления нестандартной микросхемы равна 0,02. Какое количество микросхем следует отобрать, чтобы с вероятностью 0,910 8 можно было утверждать, что доля среди них нестандартных микросхем будет
отличаться от вероятности изготовления нестандартной микросхемы по абсолютной величине не более чем на 0,05?
157.Вероятность того, что из наудачу взятого яйца выведется петушок, равна 0,52. В инкубатор заложили 38 500 яиц. Определите вероятность того, что среди выведенных цыплят число курочек будет отличаться от наиболее вероятного числа по абсолютной величине не более чем на 208 штук.
158.Известно, что 83% изделий, выпускаемых цехом по единой технологии, высшего качества. Определите вероятность того, что число изделий высшего качества среди 1 200 изготовленных будет по абсолютной величине отличаться от наиболее вероятного их числа не более чем на 10.
159.Отдел технического контроля проверяет на стандартность 900 изделий. Вероятность того, что деталь стандартна, равна 0,9. Найти с вероятностью 0,954 4 границы, в которых будет заключено число m стандартных деталей среди проверенных.
160.На керамическом заводе 70% тарелок выпускается продукцией первого сорта. ОТК завода должен проверить партию из 600 изготовленных тарелок. Какое предельное отклонение (по абсолютной величине) числа первосортных тарелок от наиболее вероятного их числа можно гарантировать с вероятностью
0,99?
161.В среднем 85% заёмщиков возвращают кредит в срок. Банк предоставил кредит 600 клиентам. Найдите вероятность того, что отклонение числа клиентов, не оплативших кредит в срок, от наивероятнейшего числа не превзойдёт 6.
162.Вероятность того, что студент воспользуется услугами банкомата 0,25. Оценить, что услугами банкомата воспользуются от 45 до 55 студентов из двухсот. Найдите вероятность того, что отклонение числа студентов, которые воспользуются банкоматом, от наивероятнейшего числа не превзойдёт трёх.
34
163.Игральную кость бросают 80 раз. Найдите приближённо границы, в которых число выпадений шестёрки будет заключено с вероятностью 0,997.
164.Вероятность поломки радиолампы в течение года – 0,1. В крае находится в эксплуатации 10 000 таких ламп. Каков должен быть объём запаса таких ламп, чтобы с надёжностью 0,95 обеспечить потребность в замене ламп?
Часть 2. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
Случайной называют величину, которая в результате испытания примет одно и только одно возможное значение, наперед неизвестное и зависящее от случайных причин, которые заранее не могут быть учтены.
Дискретной случайной величиной (ДСВ) называется случайная величина, множество значений которой конечно или бесконечно, но счётно.
Непрерывной случайной величиной (НСВ) называется случайная величина, которая принимает возможные значения из некоторого конечного или бесконечного промежутка.
2.1. Дискретные случайные величины
Законом распределения случайной величины называется соответствие между её возможными значениями и вероятностями, с которыми она их принимает.
|
|
xi |
x1 |
xi |
… |
xn |
|
|
pi |
p1 |
p2 |
|
pn |
|
n |
|
|
|
|
|
где |
pi 1 |
|
|
|
|
|
|
i 1 |
|
|
|
|
|
Пример 2.1. В магазине куплено 3 электроприбора − чайник, утюг и пылесос. Вероятность выхода из строя в течение гарантийного срока для каждого из них
соответственно равна p1 0,05, |
p2 0,1, |
p3 0,2 . Составить закон |
||
распределения случайной величины X – числа приборов, вышедших из строя в |
||||
течение гарантийного срока. |
|
|
||
Решение. X – число приборов, вышедших из строя, имеет следующие |
||||
возможные значения: |
|
|
||
x1 |
0 |
все три прибора не выйдут из строя в течение гарантийного срока; |
||
x2 |
1 |
один прибор выйдет из строя; |
|
|
x3 |
2 |
два прибора выйдут из строя; |
|
|

35
x4 3 три прибора выйдут из строя.
Найдём соответствующие этим значениям вероятности. По условию, вероятности выхода из строя приборов равны: p1 0,05; p2 0,1; p3 0,2, тогда вероятности того, что приборы будут рабочими в течение гарантийного срока, равны:
q1 |
1 |
p1 |
1 |
0,05 |
0,95; |
|
|
|
|
|
|
|
|
|
|
||
q2 |
1 |
p2 |
1 |
0,1 |
0,9; |
|
|
|
|
|
|
|
|
|
|
||
q3 |
1 |
p3 |
1 |
0,2 |
0,8. |
|
|
|
|
|
|
|
|
|
|
||
P X |
|
0 |
q1 |
q2 |
q4 |
0,95 |
0,9 |
0,8 |
0,684. |
|
|
|
|
|
|
||
P X |
|
1 q1 q2 |
p3 |
q1 p2 q3 |
p1 |
q2 |
q3 |
0,95 0,9 |
0,2 |
0,95 |
0,1 |
0,8 |
|||||
0,05 |
0,9 |
0,8 |
0,283. |
|
|
|
|
|
|
|
|
|
|
||||
P X |
|
2 |
p1 |
p2 |
|
q3 |
p1 q2 |
p3 |
q1 |
p2 |
p3 |
0,05 0,1 |
0,8 |
0,05 |
0,9 |
0,2 |
|
0,95 |
0,1 |
0,2 |
0,032. |
|
|
|
|
|
|
|
|
|
|
||||
P X |
|
3 |
p1 |
p2 |
|
p3 |
0,05 |
0,1 |
0,2 |
0,001. |
|
|
|
|
|
||
Закон распределения имеет вид:
|
X |
|
0 |
|
1 |
2 |
3 |
|
|
|
|
|
|
|
|
|
|
|
P |
|
0,684 |
|
0,283 |
0,032 |
0,001 |
|
|
|
|
|
|
|
|
|
|
Проверка: |
|
|
|
|
|
|
||
P P X 0 P X 1 P X |
2 |
P X 3 |
0,684 |
0,283 0,032 0,001 1. |
||||
Функцией распределения случайной величины называют функцию F(x), определяющую вероятность того, что случайная величина X в результате испытания примет значение меньшее x, т.е.
F x P X x .
P X x .
Свойства функции распределения
1. Значения функции распределения принадлежат отрезку 0;1 :
0F x 1.
1.
2.F x − неубывающая функция, т.е.
− неубывающая функция, т.е.
F x2  F x1 , если x2 x1 .
F x1 , если x2 x1 .
Вероятность того, что случайная величина примет значение, заключённое в интервале a, b , равна приращению функции распределения на этом интервале:
, равна приращению функции распределения на этом интервале:

|
|
|
|
|
|
|
|
|
36 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P a |
X b |
|
F b F a . |
|
|
|
|||||
Пример 2.2. Дискретная случайная величина задана законом распределения |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
|
2 |
|
4 |
|
5 |
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P |
|
0,2 |
|
0,1 |
|
0,3 |
|
0,4 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
1. Составить функцию распределения F x |
и построить ее график. 2. Найти |
|||||||||||||||||
вероятность того, что в результате испытания X примет значение, |
||||||||||||||||||
принадлежащие интервалу (3;6). |
|
|
|
|
|
|
|
|
|
|
|
|||||||
Решение. |
1. По определению, |
F x |
|
P X |
|
x , т.е. F x |
есть вероятность того, |
|||||||||||
что случайная величина X примет значение меньше, чем x. |
|
|||||||||||||||||
1. При |
|
x |
2 |
F x |
P X |
2 |
0. |
|
|
|
|
|
|
|
|
|||
2. При |
|
2 |
x |
4 |
F x |
P X |
4 |
|
P X |
2 |
0,2. |
|
|
|
|
|||
3. При |
|
4 |
x |
5 |
F x |
P X |
5 |
|
P X |
2 |
P X |
4 |
0,2 |
0,1 0,3. |
||||
4. При |
|
5 |
x |
7 |
F x |
P X |
7 |
|
P X |
2 |
P X |
4 |
|
P X |
5 |
|||
0,2 |
0,1 |
0,3 |
0,6. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5. При |
|
x |
|
7 |
F x |
P X |
2 |
P X |
4 |
P X |
5 |
P X |
7 |
|||||
0,2 |
0,1 |
0,3 |
0,4 |
1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таким образом, функция распределения примет вид:
|
0, |
x |
2 |
|
|
0,2, |
2 |
x |
4 |
F x |
0,3, |
4 |
x |
5 |
|
0,6, |
5 |
x |
7 |
|
1, |
x |
7 |
|
Построим график F(x):
F(x)
1
0,6
0,3
0,2
2 |
|
4 |
|
5 |
|
|
7 |
|
x |
|
|
|
|
||||||
Рисунок 2.1 − График функции распределения F(х). |
|||||||||
2. Найдём вероятность |
P 3 |
|
|
X |
6 |
|
по формуле P a X b F b F a , |
||
тогда P 3 X 6 F 6 F 3 |
0,6 |
0,2 |
0,4. |
||||||

37
Числовые характеристики дискретных случайных величин
Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее возможных значений на их вероятности.
M X x1 p1 x2 p2 xn pn |
n |
(2.1) |
xi pi . |
||
i |
1 |
|
Дисперсией (рассеянием) дискретной случайной величины называют математическое ожидание квадрата отклонения случайной величины от её математического ожидания:
D( X ) M X M ( X ) 2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2.2) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
При решении задач, дисперсию удобно находить по формуле |
|
|
|
|||||||||||||||||||
D( X ) M ( X 2 ) |
M ( X ) |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2.3) |
|||
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Средним квадратическим отклонением случайной величины X называют |
||||||||||||||||||||||
квадратный корень из дисперсии |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
( X ) |
|
D( X ). |
|
|
|
|
|
|
|
||||||||||||
Пример 2.3. |
Дискретная случайная величина задана законом распределения |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
X |
|
2 |
|
4 |
|
5 |
|
7 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
Р |
0,2 |
0,1 |
0,3 |
0,4 |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Найти: математическое ожидание M(X), дисперсию D(X) и среднее |
||||||||||||||||||||||
квадратическое отклонение |
|
(X ) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Решение. По |
формуле |
(2.1) |
|
|
|
|
n |
|
находим |
математическое |
||||||||||||
|
M ( X ) |
|
|
xi pi |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
i |
1 |
|
|
|
|
|
|
|
||
ожидание X: M (X ) |
2 |
0,2 |
4 |
0,1 |
5 |
0,3 |
7 0,4 |
5,1. |
|
|
|
|
|
|
|
|||||||
|
|
D( X ) M ( X 2 ) |
|
|
M ( X ) 2 и |
|
|
|
|
|||||||||||||
По формулам |
(2.3) и (2.4) |
|
|
( X ) |
|
D( X ) найдём |
||||||||||||||||
дисперсию и среднее квадратическое отклонение: |
|
|
|
|
|
|
|
|||||||||||||||
M ( X 2 ) |
n |
2 pi |
22 |
|
|
42 0,1 52 |
0,3 72 |
|
|
|
|
|||||||||||
xi |
0,2 |
0,4 |
29,5. |
|
||||||||||||||||||
|
|
|
i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5,1 2 |
|
|
|
|
|
|
|
|
|
||||||||
|
|
D( X ) |
29,5 |
|
3,49; |
( X ) |
3,49 |
|
1,87. |
|
|
|
||||||||||

38
Математические операции над случайными величинами
Пусть случайные величины X и Y заданы следующими законами распределения
X |
x1 |
x2 |
|
xn |
P |
p1 |
p2 |
|
pn |
Y |
y1 |
y2 |
|
ym |
P |
p 1 |
p 2 |
|
p m |
Две случайные величины называют независимыми, если закон распределения одной из них не зависит от того, какие возможные значения приняла другая величина. В противном случае случайные величины зависимы. Несколько случайных величин называют взаимно независимыми, если законы распределения любого числа из них не зависят от того, какие возможные
значения приняли остальные величины. |
Будем рассматривать независимые |
||||||||||||||||||||||||||
случайные величины. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Произведением постоянной С на случайную величину X называется новая |
|||||||||||||||||||||||||||
случайная величина Z CX , |
которая |
принимает |
свои |
значения |
|
zi |
|
|
|
Cxi |
с |
||||||||||||||||
вероятностями P Z |
zi |
P X |
xi . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
m-й степенью случайной величины Х |
называется |
|
случайная |
||||||||||||||||||||||||
величина Z |
X m , которая |
принимает свои |
значения z |
i |
xm i |
с вероятностями |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P Z |
|
zi |
P X xi . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Суммой двух случайных величин X и Y называется случайная величина |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Z |
X |
Y , |
принимающая |
все |
значения |
|
zk |
xi |
y j ; |
i |
|
(1, n); j |
|
(1, m) , |
с |
||||||||||||
вероятностями P(Z |
zk ) |
P(x |
xi ) P(Y |
y j ) , для всех указанных значений i и j. |
|||||||||||||||||||||||
Разностью двух случайных величин X и Y называется случайная величина |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Z |
X |
Y , |
принимающая все |
значения |
zk |
xi |
y j ; |
i |
(1, n); j |
(1, m) , |
с |
||||||||||||||||
вероятностями P(Z |
zk ) |
P(x |
xi ) P(Y |
y j ) , для всех указанных значений i и j. |
|||||||||||||||||||||||
Произведением двух случайных величин X и Y называется случайная |
|||||||||||||||||||||||||||
величина Z XY , принимающая все значения |
|
|
|
|
|
|
|
|
|
|
, с |
||||||||||||||||
zk |
xi y j ; |
i |
(1, n); |
j |
(1, m) |
||||||||||||||||||||||
вероятностями P(Z |
zk ) |
P(x |
xi ) P(Y |
y j ) , для всех указанных значений i и j. |
|||||||||||||||||||||||

39
Пример 2.4. Независимые случайные величины X и Y заданы законами распределения:
|
X |
1 |
|
3 |
|
4 |
|
|
|
Y |
0 |
|
2 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P |
0,1 |
|
? |
|
0,6 |
|
|
Р |
0,2 |
|
0,4 |
? |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а) найти P(X |
|
3), P(Y |
3); |
|
|
|
|
|
|
|||||
б) составить закон распределения случайной величины Z X |
Y. |
|
|
|||||||||||
Найти M(Z), D(Z) и проверить выполнение свойств |
|
|
|
|
||||||||||
M (X Y) M (X ) M (Y); D(X Y) D(X ) D(Y); |
|
|
|
|
||||||||||
в) составить закон распределения V |
X Y . Найти M(V) и проверить |
|
|
|||||||||||
выполнение свойства M (X Y) M (X ) |
M (Y). |
|
|
|
|
|||||||||
|
Решение: а) Так как |
|
|
|
|
|
|
|||||||
P( X 1) P( X 3) P( X 4) 1, P(Y 0) P(Y 2) P(Y 3) 1, |
|
|
|
|
||||||||||
то P( X |
3) |
|
1 |
(0,1 |
0,6) 0,3, P( X 3) |
1 (0,2 0,4) 0,4. |
|
|
|
|
|
|||
Запишем закон распределения случайных величин X и Y . :
X |
1 |
3 |
4 |
|
|
|
|
P |
0,1 |
0,3 |
0,6 |
|
|
|
|
Y |
0 |
2 |
3 |
|
|
|
|
Р |
0,2 |
0,4 |
0,4 |
|
|
|
|
б) Найдём возможные значения случайной величины Z X Y, которые равны суммам каждого возможного значения величины X с каждым возможным значением величины Y. Их соответствующие вероятности равны произведениям вероятностей слагаемых:
|
|
|
Z X |
Y |
|
1+0=1 |
1+2=3 |
|
|
1+3=4 |
|
|
|
3+0=3 |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P |
|
|
0,1 |
0,2 |
0,02 |
0,1 |
0,4 |
0,04 |
|
0,1 |
0,4 |
0,04 |
|
|
0,3 |
0,2 |
0,06 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
3+2=5 |
|
|
3+3=6 |
|
4+0=4 |
|
|
|
|
4+2=6 |
|
|
|
|
4+3=7 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
0,3 |
0,4 |
0,12 |
0,3 |
0,4 |
0,12 |
|
0,6 |
0,2 |
0,12 |
|
0,6 |
0,4 |
0,24 |
|
0,6 |
0,4 |
0,24 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
Одинаковые значения величины Z объединяем, складывая их вероятности. |
|||||||||||||||||||||||||||||
Закон распределения случайной величины Z будет иметь вид: |
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
Z |
X |
Y |
1 |
|
3 |
|
|
4 |
|
|
5 |
|
6 |
|
|
|
|
7 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
P |
|
0,02 |
|
|
0,1 |
|
0,16 |
|
0,12 |
|
0,36 |
|
0,24 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

40
M (Z ) |
1 0,02 |
3 |
0,1 |
4 |
0,16 |
|
|
5 |
|
0,12 |
|
6 |
|
0,36 |
|
7 0,24 |
5,4; |
|
|
|
|
|
|
||||||||||||||||||
M ( X ) |
1 0,1 |
|
3 |
0,3 |
4 |
0,6 |
|
3,4; M (Y ) |
0 |
0,2 |
2 |
0,4 |
3 |
0,4 |
2; |
|
|
|
|
||||||||||||||||||||||
M ( X ) M (Y ) 3,4 2 |
|
5,4. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Итак, M ( X Y ) |
|
|
M ( X ) |
|
|
M (Y ); |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
M (Z 2 ) |
1 0,02 |
|
9 0,1 |
16 |
0,16 |
|
25 0,12 |
|
36 |
0,36 |
43 0,24 |
|
31,2; |
|
|
|
|
||||||||||||||||||||||||
D(Z ) |
M (Z 2 ) |
|
|
|
M (Z ) 2 |
|
31,2 |
|
|
5,4 2 |
2,04; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
M ( X 2 ) |
1 0,1 |
9 |
0,3 |
16 |
0,6 |
|
12,4; D(X) |
12,4 - (3,4)2 |
0,84; |
|
|
|
|
||||||||||||||||||||||||||||
M (Y 2 ) |
0 |
0,2 |
|
|
4 |
0,4 |
|
9 |
0,4 |
|
5,2; D(Y ) |
|
5,2 |
|
22 |
1,2; |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
D( X ) D(Y ) 0,84 1,2 |
|
|
2,04. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Итак : D( X |
Y ) |
|
D( X ) |
|
D(Y ). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
в) Составим |
|
|
закон |
|
распределения |
V |
X Y . |
Найдём |
возможные значения |
||||||||||||||||||||||||||||||||
случайной величины V, |
|
которые |
|
равны произведениям каждого возможного |
|||||||||||||||||||||||||||||||||||||
значения X на каждое возможное значение Y. Их соответствующие вероятности |
|||||||||||||||||||||||||||||||||||||||||
равны произведениям вероятностей сомножителей: |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
V X Y |
1 0 0 |
|
1 2 2 |
|
1 3 3 |
3 0 0 |
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
P |
|
|
|
|
|
|
0,02 |
|
|
|
|
0,04 |
|
|
|
0,04 |
|
|
0,06 |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
3 2 |
|
6 |
|
|
|
3 3 |
9 |
|
|
4 0 |
|
0 |
|
4 2 |
8 |
|
|
4 3 |
|
12 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
0,12 |
|
|
|
|
|
0,12 |
|
|
|
|
|
0,12 |
|
|
|
|
0,24 |
|
|
|
0,24 |
|
|
||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
Одинаковые значения величины V |
X Y объединяем, складывая их |
||||||||||||||||||||||||||||||||||||||||
вероятности. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Закон распределения V |
|
|
X Y записываем так: |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
V |
|
|
X Y |
|
|
|
0 |
|
|
|
2 |
|
|
|
|
3 |
|
6 |
|
|
|
8 |
|
|
|
|
9 |
|
12 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
P |
|
|
|
0,2 |
|
|
|
0,04 |
|
0,04 |
|
0,12 |
|
0,24 |
|
0,12 |
|
0,24 |
|
||||||||||||||
Найдём |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
M (V ) |
0 0,2 |
|
|
2 0,04 |
|
3 0,04 |
6 |
0,12 |
8 |
0,24 |
9 |
0,12 |
12 |
0,24 |
6,8. |
|
|||||||||||||||||||||||||
M ( X ) M (Y ) |
|
|
3,4 |
2 |
|
|
6,8. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Таким образом, M (X Y) |
M (X ) |
|
M (Y). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
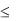
41
Задачи
165. Какие из перечисленных ниже случайных величин являются дискретными: а) число студентов в группе, сдавших экзамен на «отлично»; б) число бракованных изделий в отобранной на проверку партии; в) отклонение размера обрабатываемой детали от стандарта; г) число
посетителей отделения сбербанка |
в течение дня; д) время обслуживания |
||||||
покупателя кассиром; е) время ожидания пассажиром автобуса. |
|||||||
166. Известен закон распределения случайной величины Х: |
|||||||
|
xi |
|
|
6 |
|
10 |
|
|
2 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
pi |
0,5 |
|
0,4 |
|
0,1 |
|
Найти функцию распределения и построить её график. Определить вероятность того, что в результате испытания случайная величина примет значение: а) меньше 5; б) не меньше 7; в) заключённое в интервале (0;8).
167. Доход от финансовой операции подчиняется закону распределения Х:
xi |
0 |
1 |
2 |
3 |
pi |
0,2 |
0,3 |
0,4 |
? |
Найти: а) вероятность p(x = 3); б) функцию распределения этой случайной величины и построить её график . б) Определить аналитически и показать на графике P(1 x < 3).
168. Дискретная случайная величина Х задана законом распределения :
xi |
4 |
6 |
8 |
10 |
pi |
0,1 |
0,25 |
0,45 |
0,2 |
|
|
|
|
|
Вычислить математическое ожидание, дисперсию, среднее квадратическое отклонение.
169. Дискретная случайная величина Х задана законом распределения :
xi |
-10 |
-4 |
0 |
10 |
|
|
|
|
|
pi |
0,15 |
0,25 |
0,45 |
0,15 |
|
|
|
|
|
Найти функцию распределения и построить её график. Вычислить математическое ожидание, дисперсию, среднее квадратическое отклонение.
170. Изучение спроса изделий некоторой фирмы дало распределение случайной величины Х – числа потребляемых за месяц изделий:

|
|
|
42 |
|
|
|
|
|
|
|
xi |
|
10 |
|
20 |
|
30 |
|
40 |
|
50 |
0 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
pi |
0,1 |
0,1 |
|
0,2 |
|
0,3 |
|
0,1 |
|
0,2 |
Составить функцию распределения F(x), построить её график. Найти среднее число изделии, потребляемых в течение месяца. Найти вероятность того, что за месяц будет продано от 25 до 40 изделий данной фирмы.
171. Функция распределения случайной величины Х дискретного вида имеет следующий вид:
|
0, |
если |
|
x |
1 |
|
F (x) |
0,2 , |
если |
1 |
x |
2 |
|
0,5, если |
2 |
x |
3 |
|
||
|
|
|||||
|
1, |
если |
|
x |
3 |
|
Найти закон распределения, математическое ожидание и |
дисперсию |
|||||
случайной величины Х. |
|
|
|
|
|
|
172. Случайная величина Х принимает только два значения x1 |
и x2 , причём |
|||||
x1 x2 . Вероятность того, что Х примет значение x1 равна 0,2. |
Найти закон |
|||||
распределения Х , зная что М(Х)= 2,6 , |
σ(Х)=0,8 . |
|
|
|||
173. Случайная величина Х принимает три возможных значения: -1; 0; 1 с
вероятностями , соответственно p1 , p2 , p3 |
|
. Найти закон распределения Х , если |
||||||||||
известны М(Х)= 0,3 , М(Х2)=0,7 . |
|
|
|
|
|
|
|
|
|
|||
174. Случайная величина Х имеет следующее распределение: |
|
|||||||||||
|
xi |
|
– 1 |
|
|
0 |
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
pi |
|
0,2 |
|
|
0,3 |
|
0,4 |
|
0,1 |
|
|
Составить законы распределения: |
|
|
|
|
|
|
|
|
|
|||
а) Y1 = 3X ; б) Y2 = X2 ; в) Y3 = (X – 1)2 и найти их числовые характеристики. |
||||||||||||
175. Закон распределения случайной величины Х имеет вид : |
|
|||||||||||
|
xi |
|
– 1 |
|
0 |
|
|
|
|
|
||
|
|
|
|
2 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
pi |
|
0,6 |
|
0,3 |
|
0,1 |
|
|
|
|
|
а) составить закон распределения случайных величин Y = 2X, Z = X + X и |
||||||||||||
убедиться, что это различные случайные величины, т.е., что Y |
Z; б) вычислить |
|||||||||||
математические ожидания и дисперсии случайных величин |
2X и X + X; |
|||||||||||
в) можно ли для Z = X + X применить теорему о дисперсии суммы случайных величин?
43
В задачах 176 – 180 даны законы распределения двух независимых случайных величин Х и Y. Требуется: а) составить закон распределения случайной величины Z; б) найти числовые характеристики случайной величины Z; в) составить функцию распределения Z и построить её график.
176.
|
xi |
2 |
5 |
8 |
|
уi |
2 |
4 |
|
6 |
|
|
pi |
0,7 |
0,1 |
0,2 |
|
pi |
0,35 |
0,4 |
|
0,25 |
|
Z = X + 2Y. |
|
|
|
|
|
|
|
|
|
||
177. |
|
|
|
|
|
|
|
|
|
|
|
|
xi |
|
6 |
|
|
уi |
|
|
|
25 |
|
|
3 |
9 |
|
5 |
15 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
pi |
0,6 |
0,3 |
0,1 |
|
pi |
0,9 |
0,05 |
0,05 |
|
|
Z = 3Х – 5Y.
178. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xi |
|
– 1 |
|
0 |
|
2 |
|
уi |
|
1 |
|
3 |
|
5 |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
pi |
|
0,4 |
|
0,5 |
|
0,1 |
|
pi |
|
0,2 |
|
0,5 |
|
0,3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z = X ∙ Y. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
179. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xi |
|
|
|
|
уi |
|
|
|
5 |
|
|||||
|
|
2 |
|
3 |
|
4 |
|
|
3 |
|
4 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
pi |
|
0,2 |
|
0,4 |
|
0,4 |
|
pi |
|
0,3 |
|
0,4 |
|
0,3 |
|
Z = (2X) ∙ Y. |
|
|
|
|
|
|
|
|
|
|
|
|||||
180. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xi |
|
|
|
|
уi |
|
– 1 |
|
|
2 |
|
||||
|
|
2 |
|
4 |
|
6 |
|
|
|
0 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
pi |
|
0,6 |
|
0,2 |
|
0,2 |
|
pi |
|
0,15 |
|
0,25 |
0,6 |
|
|
Z= Y3 + X2.
181.Доходность Х, Y (тыс. руб.) двух видов ценных бумаг подчиняются следующим законам распределения:
xi |
– 1 |
0 |
2 |
|
уi |
0 |
1 |
2 |
pi |
0,2 |
0,4 |
0,4 |
|
pi |
0,4 |
0,5 |
0,1 |
|
|
|
|
|
|
|
|
|
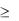
44
Определить среднюю доходность этих бумаг. Составить функцию распределения суммы этих случайных величин (доходность портфеля из этих бумаг). Найти вероятность того, что доходность портфеля будет: а) не менее 2 тыс. руб.; б) не более 0.
182. Сумма выплат по договору страхования описывается законом распределения
|
xi (тыс. руб.) |
0 |
1 |
2 |
|
|
|
pi |
0,7 |
0,2 |
0,1 |
|
|
|
|
|
|
|
|
|
Составить функцию распределения случайной величины S – суммы выплат |
||||||
по трём договорам страхования и найти вероятность того, что S 4 |
тыс. руб. |
|||||
Построить её график. |
|
|
|
|
|
|
183. На двух автоматических станках |
производятся одинаковые |
изделия. |
||||
Даны законы распределения числа бракованных изделий, производимых в
течение смены на каждом из них: |
|
|
|
|
|
|
||||||
для первого |
|
|
|
для второго |
|
|
||||||
Х |
|
1 |
|
2 |
|
У |
|
0 |
|
2 |
|
|
|
0 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Р |
|
0,1 |
0,6 |
|
0,3 |
|
Р |
|
0,5 |
|
0,5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Составить |
закон распределения |
числа производимых в течение смены |
|||||||||
бракованных изделий обоими станками. Составить функцию распределения и построить её график. Проверить свойство математического ожидания суммы случайных величин.
184. Законы распределения независимых случайных величин Х и Y даны в
таблицах: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
хi |
|
2 |
|
4 |
|
5 |
|
yi |
|
0 |
|
3 |
|
4 |
|
1 |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
рi |
0,1 |
0,35 |
|
0,25 |
|
0,3 |
|
рj |
|
0,2 |
|
0,5 |
|
0,3 |
Составить закон распределения случайной величины Z = X + 2Y. Проверить на этом примере свойства математического ожидания и дисперсии суммы случайных величин и произведения постоянной величины на случайную.
185.Случайные величины X и Y независимы. Найти дисперсию случайной величины Z = 3X + 2Y , если известно, что D(X) = 5, D(Y) = 6.
186.X, Y, Z – случайные величины: Х – выручка фирмы, Y – затраты фирмы, Z = X – Y – прибыль. Найти распределение прибыли и её среднее значение, если выручка и затраты заданы распределениями:

|
|
|
|
|
45 |
|
|
|
|
|
Х |
|
4 |
|
5 |
|
У |
|
1 |
|
2 |
3 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
Р |
1/3 |
1/3 |
|
1/3 |
|
Р |
|
0,5 |
|
0,5 |
|
|
|
|
|
|
|
|
|
|
|
187. Х – выручка фирмы в долларах. Найти распределение выручки в рублях Z = X ∙ Y и её среднее значение в пересчёте по курсу доллара, если выручка Х не зависит от курса Y, а распределения Х и Y имеют вид:
Х |
1000 |
2000 |
|
У |
25 |
26 |
27 |
28 |
|
|
|
|
|
|
|
|
|
Р |
0,7 |
0,3 |
|
Р |
0,2 |
0,2 |
0,45 |
0,15 |
|
|
|
|
|
|
|
|
|
188. Найти математическое ожидание числа очков, выпадающих на игральной кости при одном бросании. Найти математическое ожидание суммы и произведения числа очков, выпадающих при одновременном бросании двух игральных костей M (X+Y), M(X Y).
189.Сделано два высокорискованных вклада: 10 тыс. руб. в компанию А и 15 тыс. руб. – в компанию В. Компания А обещает 50% годовых, но может «лопнуть» с вероятностью 0,2. Компания В обещает 40% годовых, но может «лопнуть» с вероятность 0,15. Составить закон распределения случайной величины – общей суммы прибыли, полученной от двух компаний через год, и найти её математическое ожидание.
190.Вероятность своевременной поставки продукции для каждого из трёх поставщиков соответственно равны 0,8; 0,9; 0,6. Составить закон распределения случайной величины Х – числа поставщиков, своевременно поставивших продукцию. Найти числовые характеристики Х.
191.Партия из 6 телевизоров содержит 2 неисправных. Из этой партии наугад выбирают 3 телевизора. Найти закон распределения случайной величины
Х– количества неисправных телевизоров среди выбранных. Определить математическое ожидание и дисперсию.
192.Клиенты банка, не связанные друг с другом, не возвращают кредиты в срок с вероятность 0,1. Составить закон распределения числа возвращённых в срок кредитов из 5 выданных. Составить функцию распределения и построить её график. Найти математическое ожидание и дисперсию случайной величины.
193.В лотерее 1 000 билетов, из них на один билет падает выигрыш
в 1 000 руб., на 10 билетов – выигрыш по 500 руб., на 50 билетов – выигрыш по 200 руб., на 100 билетов – выигрыш по 50 руб., остальные билеты невыигрышные. Составить закон Х – суммы выигрыша на один билет.

46
194.Продавец мороженого в солнечный день может продать мороженого на 2 тыс. руб., а в дождливый – на 200 руб. Составить закон распределения ожидаемой дневной выручки, если вероятность того, что день окажется дождливым, равна 0,2.
195.С целью получения займа предприниматель обращается в один из четырёх банков. В случае отказа в займе он обращается в следующий и так далее. Вероятность получения займа в первом банке равна 0,6, для каждого последующего она возрастает на 0,1. Случайная величина Х – количество банков, в которые обратится предприниматель. Составить закон распределения
этой случайной величины и найти вероятность того, что 2 Х < 4.
196.При выполнении условий контракта фирма с вероятностью р1 = 0,9 получит прибыль, равную 10 000 руб. и с вероятностью р2 = 0,1 получит прибыль равную 40 000 руб. При невыполнении условий контракта фирма уплачивает 20 000 руб. Случайная величина Х – доход фирмы от контракта. Составить закон распределения случайной величины Х, если вероятность выполнения условий контракта фирмой равна 0,7. Найти математическое ожидание и дисперсию.
197.Некий человек, имея 4 ключа, хочет открыть дверь. При этом он подбирает ключи случайно. Найти математическое ожидание и дисперсию числа испытаний при следующих условиях: а) испробованный ключ не устраняется из дальнейшего выбора; б) устраняется (предполагается, что только один ключ подходит к двери).
198.Два баскетболиста делают по два броска мячом в корзину. Вероятности попадания мяча в корзину при броске для каждого спортсмена соответственно равны 0,3 и 0,4. Составить распределения Х – числа попаданий в корзину, найти математическое ожидание и дисперсию случайной величины Х.
199.Отдел технического контроля проверяет изделия на стандартность. Вероятность того, что изделие стандартно, равна 0,9. В каждой партии содержится 5 изделий. Найти математическое ожидание случайной величины
Х– числа партий, в каждой из которых окажется ровно 4 стандартных изделия, если проверке подлежит 50 партий.
200.Подбрасывается 5 игральных костей, общее число подбрасываний равно
20. Найти математическое ожидание и дисперсию дискретной случайной величины Х – числа таких бросаний пяти игральных костей, в каждом из которых на двух костях появится по одному очку.

47
201. Дискретная случайная величина задана законом распределения:
Х 2 3 4
Р0,1 0,4 0,5
Найти начальные моменты первого, второго, третьего и четвёртого порядков. 202. Дискретная случайная величина Х задана законом распределения
Х 1 3 4
Р0,1 0,6 0,3
Найти центральные моменты первого, второго, третьего и четвёртого порядков.
203.В магазин вошли 3 покупателя. Вероятности того, что каждый из них совершит покупку, соответственно равны 0,8, 0,7, 0,6. Составить закон распределения числа покупателей, совершивших покупку, вычислите начальный момент первого порядка и центральный момент второго порядка.
204.В городе 9 машиностроительных предприятий, из которых 6 рентабельных и 3 убыточных. Программой приватизации намечено приватизировать 5 предприятий. При условии проведения приватизации в случайном порядке составить закон распределения рентабельных предприятий, попавших в число приватизируемых. Найти начальные и центральные моменты второго порядка.
2.2. Непрерывные случайные величины и их числовые характеристики
Случайная величина Х, для которой функция распределения вероятностей F(x) непрерывна , называется непрерывной.
Плотностью распределения вероятностей непрерывной случайной величины X называют функцию f x − первую производную от функции распределения F x : f x
− первую производную от функции распределения F x : f x F
F x .
x .
Свойства плотности распределения
1. Плотность распределения – неотрицательная функция:
fx 0 .
0 .
2.Вероятность того, что непрерывная случайная величина X примет значение, принадлежащее интервалу (a,b), равна определённому интегралу от плотности распределения, взятому в пределах от а до b:
|
b |
P a X b |
f x dx. |
a
