
- •Содержание
- •Введение
- •1.2. Рыночная экономика, её достоинства и недостатки
- •Контрольные вопросы
- •Глава 2. Рыночный механизм: исходный анализ спроса и
- •предложения и его применение
- •2.2. Индивидуальное и рыночное предложение в системе рынка, факторы, его определяющие
- •Глава 3. Эластичность спроса и предложения
- •3.2. Эластичность спроса по доходу и эластичность предложения
- •3.3. Перекрёстная эластичность спроса и предложения
- •Контрольные вопросы
- •Глава 4. Теория потребительского выбора
- •4.1. Количественный подход к анализу общей и предельной полезности. Критерий рациональности поведения потребителя. Законы Госсена
- •4.2. Порядковая теория полезности. Оптимальный выбор потребителя
- •5.2. Расширение производства в краткосрочном и долгосрочном периодах
- •5.3. Минимизация издержек производства фиксированного продукта.
- •Равновесие производителя
- •6.2. Монополия и монопольная власть
- •6.3. Монополистическая конкуренция и олигополия
- •7. 1. Предложение и спрос на рынке труда
- •Рисунок 7.1 – Кривая предложения и равновесие на рынке труда
- •Рисунок 7.2 – Эффект замены и эффект дохода на рынке труда
- •Рисунок 7.3 – Равновесие конкурентной фирмы на рынке труда
- •Поток наличности в течение года
- •Таблица 7.2 – Ранжирование инвестиционных проектов
- •8.1 Положительные и отрицательные внешние эффекты
- •Рисунок 8.2 – Положительные внешние эффекты в конкурентной отрасли
- •Таблица 8.1 – Выпуск мяса, потери рыбы и прибыли производителей мяса
- •Рисунок 8.3 – Оптимальный выпуск общественного блага

потраченной на покупку какого-либо товара, одинакова, независимо от того, на какой товар она израсходована.
Иначе это можно сформулировать так: отношение предельной полезности блага к его цене должно быть одинаковым для всех благ.
MU A |
|
MU B |
|
MU N |
. |
|
|
|
|
||
PA |
|
PB |
|
PN |
|
4.2. Порядковая теория полезности. Оптимальный выбор потребителя
Всоздание и развитие порядковой или ординалистской (ordinal) теории полезности внесли свой вклад такие экономисты, как Ф. Эджуорт, В. Парето, И. Фишер. Появилась она на основе критики количественной теории полезности. В 30-х годах ХХ века после работ Р. Алена и Дж. Хикса эта теория стала общепринятой и поныне остается наиболее распространённой.
Врыночной экономике потребитель свободен в своём выборе товаров и услуг, но органичен доходом и рыночными ценами. Потребитель ведёт себя рационально, т.е. стремится приобрести такие товары и услуги, которые принесут ему максимальную полезность. Согласно порядковой теории полезности потребитель сравнивает и оценивает не отдельные товары, а наборы, состоящие из n товаров. Выбор потребителем одного из множества других наборов показывает его предпочтения (preferences). Поведение рационального потребителя подчиняется определённым аксиомам4, с которыми согласуются его предпочтения.
Обратимся к аксиомам порядковой теории полезности.
1. Аксиома полной (совершенной) упорядоченности. Потребитель всегда способен упорядочить (сравнить) альтернативные наборы товаров с помощью отношений предпочтения ( , ), или безразличия (~ ).
2. Аксиома транзитивности. Данная аксиома характеризует согласованность
предпочтений: а) если А В С, |
то А С; |
б) если А В ~С, А~ В С, то |
А ~ С |
4 Аксиома – это положение, принимаемое без логического доказательства, в силу его непосредственной убедительности; истинное исходное положение теории.
в) если А ~ В ~ С, то А ~ С.
3.Аксиома ненасыщения. Если набор товаров А содержит не меньшее количество каждого товара, а одного из них больше, чем набор В, то А В .
4.Аксиома независимости потребителя. Удовлетворение потребителя зависит только от количества потребляемых им благ и не зависит от количества благ, потребляемых другими.
В порядковой теории полезности понятие «полезность» означает не более чем порядок предпочтения. Задача максимизации полезности сводится к задаче выбора потребителем наиболее предпочтительного товарного набора из всех допустимых до него.
Порядковая функция полезности в противоположность количественной позволяет лишь судить о том, какой набор товаров предпочтительнее, и не даёт возможности оценивать и сравнивать разницу в полезности наборов. Для набора, состоящего из двух благ, функция полезности имеет вид U = U(X, У).
Предельная полезность (MUi – marginal utility) i-го блага показывает приращение полезности набора при изменении объёма потребления i-го блага на единицу и при неизменном объёме потребления других благ.
Мы можем представить потребительские предпочтения графически, используя кривые безразличия (рисунок 4.3).
Кривые безразличия – это линии, соединяющие наборы равной полезности на плоскости благ. Исследуем свойства кривых безразличия.
|
У |
|
|
|
|
|
Свойство 1. Кривая безразличия, |
|||
|
|
|
|
|
|
|
|
лежащая выше и |
правее |
другой |
|
|
|
А |
|
|
|
|
кривой, представляет собой более |
||
У1 |
|
|
D |
|
|
|
|
|||
|
|
|
|
|
|
|
|
предпочтительные |
для |
данного |
|
|
|
В |
|
|
|
|
потребителя наборы товаров. |
||
|
|
|
|
|
|
U2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U1 |
|
На рисунке 4.3 |
U2 >U1. |
Данное |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
свойство поддерживается утвержде- |
||
|
|
|
|
|
|
|
||||
|
Х1 |
Х2 |
|
|
|
X |
||||
|
|
|
|
нием о монотонном возрастании |
||||||
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|||
|
Рисунок 4.3 – |
Кривые |
|
|||||||
|
|
|
|
|
||||||
функции полезности.
|
У |
|
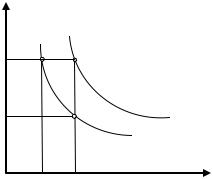
Свойство 2. Кривые безразличия |
|||||||||
|
|
|
|
|
|
не могут |
пересекаться, |
так |
как |
|||
|
|
А |
|
являются |
геометрическим |
местом |
||||||
У1 |
|
D |
|
|||||||||
|
|
|
|
|
|
наборов равной полезности. |
|
|||||
|
|
В |
|
Предположим, что две кривые |
||||||||
|
|
|
|
U2 |
|
|||||||
|
|
|
|
U1 |
|
безразличия пересекаются в точке В |
||||||
0 |
|
|
|
|
|
(рисунок |
4.4). |
Тогда, |
по |
|||
|
Х1 Х2 |
|
|
X |
определению |
кривой |
безразличия |
|||||
|
|
|
|
|||||||||
|
|
|
|
|
|
|||||||
Рисунок 4.4 – Кривые безразличия не |
||||||||||||
А~ В; D~В. |
|
|
|
|
|
|||||||
пересекаются |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
||||||
Из аксиомы транзитивности следует, что если А ~ В, а D ~ В, то |
А ~ D, но это |
|||||||||||
неверно, |
на самом деле D А (аксиома ненасыщения). |
Следовательно, |
две |
|||||||||
кривые не могут иметь общую точку, т.к. один набор товаров не может характеризоваться различными уровнями полезности.
У |
|
|
|
|
|
|
|
|
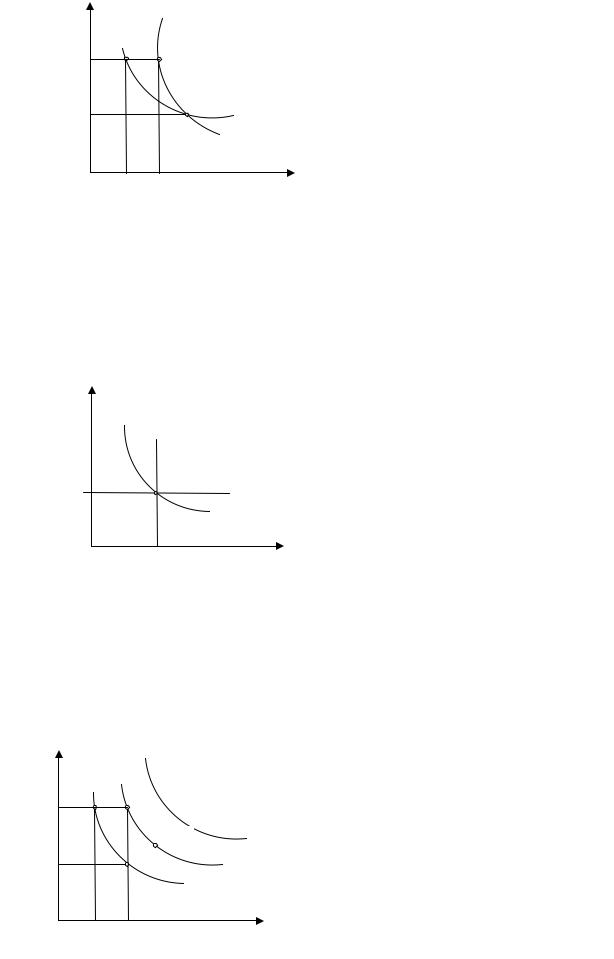
Свойство 3. |
Кривые |
безразличия |
||||
|
|
|
|
|
|
|
|
строго выпуклы к началу координат и |
|||||||
|
|
|
|
|
|
|
|
|
|
||||||
У1 |
|
|
|
|
|
|
|
|
имеют отрицательный наклон. |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
Пусть |
дана |
|
некоторая |
точка А |
||||
|
|
II |
|
|
III |
|
|
|
|||||||
|
|
|
А |
|
(рисунок |
4.5), |
характеризующая |
||||||||
|
|
|
|
|
|
|
|
U2 |
|
||||||
|
|
|
|
|
IV |
U1 |
|
|
определённую |
комбинацию |
товаров. |
||||
|
|
I |
|
|
|
|
|||||||||
0 |
|
|
|
|
|
|
|
|
|
Проведём |
через |
неё |
две |
взаимно |
|
|
|
|
|
|
|
|
|
|
|||||||
|
Х1 |
Х2 |
|
|
|
|
X |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
перпендикулярные прямые. Очевидно,. |
|||||||||
Рисунок 4.5 – Отрицательный |
|
||||||||||||||
|
|
|
|
|
|
|
|||||||||
наклон кривых безразличия |
|
что в |
соответствии |
с |
аксиомой |
||||||||||
ненасыщения, любой набор товаров из
квадранты III предпочтительнее, чем набор товаров А. По этой же причине набор |
|||||
товаров А предпочтительнее любого набора из квадранта I. Следовательно, все |
|||||
|
У |
|
|
|
наборы товаров, имеющие равный с |
|
|
|
|
|
набором А уровень полезности, должны |
У1 |
|
А |
С |
|
лежать в квадрантах II и IV. Иными словами |
|
|
U3 |
|
||
|
|
|
|
кривая безразличия имеет отрицательный |
|
|
|
|
|
|
|
|
|
|
D |
|
наклон. |
|
|
|
В |
|
|
|
|
|
U2 |
|
|
|
|
|
|
|
|
|
|
|
U1 |
|
|
0 |
Х1 |
Х2 |
|
|
X |
|
|
|
|||
Рисунок 4.6 – Карта кривых |
|
|
|||
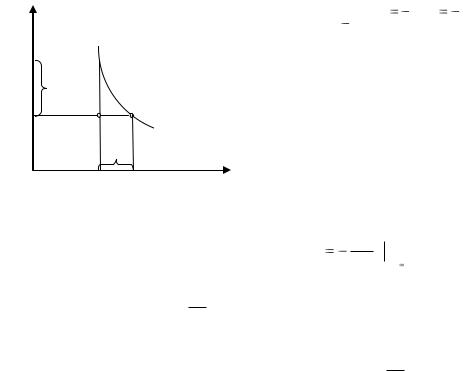
Свойство 4. Кривая безразличия может быть проведена через любую точку пространства товаров (аксиома полной упорядоченности).
Таким образом, мы получаем множество кривых безразличия – карту кривых безразличия, содержащую информацию о системе предпочтений потребителя.
Потребитель может изменить структуру своего потребления, замещая некоторое количество одного блага другим благом и сохраняя неизменным уровень полезности набора.
Пусть потребитель безразличен в выборе между наборами А и В (рисунок 4.7).Значит, норма, по которой он согласен замещать благо Y благом Х, оставаясь при этом на одной и той же кривой безразличия, составит:
У
У1  А
А
∆У
КВ
U1
∆Х
0 |
Х1 |
Х2 |
X |
|
Рисунок 4.7 – Убывание предельной нормы замещения двух благ.
OY1 |
- OY2 |
|
ΔY |
|
AK |
. |
|
|
|
|
|
|
|
OX1 |
OX 2 |
|
ΔX |
|
KB |
|
|
|
|
Предельной нормой замещения благом Х блага Y (MRSxy) называют количество блага Y, которое должно быть сокращено «в обмен» на увеличение количества блага Х на единицу с тем, чтобы уровень удовлетворения потребителя остался неизменным.
MRSxy ΔY
ΔX U const
Поскольку отношение ΔY по определению отрицательное, минус вводится
ΔX
перед правой частью, делает значение нормы замещения положительным. По мере приближения точки А к точке В отношение AK будет приближаться к
KB
наклону касательной в точке В. В пределе в окрестностях точки В наклон кривой (или касательной) в этой точке и есть предельная норма замещения.
Предельная норма замещения может принимать различные значения.
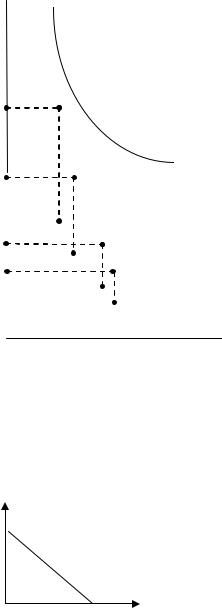
Y
Y0 A
Y1 К B
Y2
Y3
0 |
X0X1 X2 X3 |
X |
Рисунок 4.8 – MRSxy убывает
1. MRSxy может меняться при движении вдоль кривой безразличия.
В случае выпуклости к началу координат. MRS убывает по мере замещения одного блага другим, т.е. потребитель соглашается отдавать все меньшее количество замещаемого блага за одно и то же количество замещающего.
|
|
Так на рисунке 4.8 потребитель, находясь в |
У |
|
точке А, готов уступить Y0Y1 блага Y взамен |
|
|
приращения блага Х на Х0Х1. Однако, |
|
|
располагая набором С, он за равновеликое |
U1 |
|
приращение блага Х (Х2Х3=Х0Х1) согласится |
|
|
|
|
|
уступить лишь Y2Y3 блага Y, что меньше |
0 |
X |
Y0Y1. |
Рисунок 4.9 – |
|
|
MRSxy = const |
|
2. MRSxy = const для двух совершенно
взаимозаменяемых товаров.
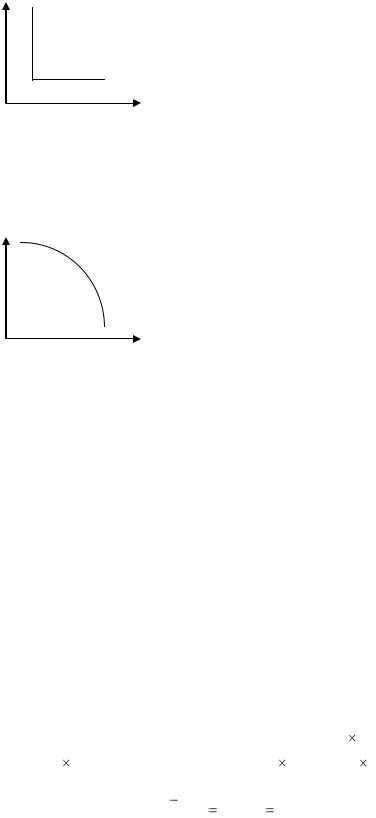
В этом случае кривые безразличия вырождаются в прямые линии. Обычно такие товары рассматриваются как один товар (рисунок 4.9).
У
U1
0
X
Рисунок 4.10 – MRSxy = 0
У
U1
0
X
Рисунок 4.11 – MRS xy возрастает
3. MRSxy = 0 в том случае, когда товары вообще не могут заменять друг друга, например правый и левый ботинок.
Потребитель получит одно и то же удовлетворение, имея один левый и два правых ботинка или просто левый и правый ботинок. Такие товары жёстко дополняют друг друга (рисунок 4.10).
4. MRSxy возрастает по мере замещения одного блага другим. Это возможно, когда чем больше какого-то товара имеет потребитель, тем больше он хотел бы его иметь. В этом случае кривая безразличия вогнута к началу координат (рисунок 4.11). Хотя не один из вариантов не может быть исключён, выпуклость кривых безразличия и убывающая норма замещения представляют наи-
более общую и распространённую ситуацию.
Количественная и порядковая теории полезности – это теории, построенные на основе различных предположений о поведении потребителей. Тем не менее в этих теориях можно обнаружить много общего. В частности, кривые безразлчия в порядковой теории можно рассматривать как линии уровня функции общей полезности U = f (X, Y) в количественной теории.
Предельную норму замещения вдоль кривой безразличия можно связать с предельными полезностями блага на каждой из осей. Изъятие товара Y наносит
потребителю ущерб. Потеря полезности = ─ ∆ Y |
MUY; приобретённая |
||||
полезность = ∆Х MUx. Таким образом, ─ ∆ Y MUY = ∆Х |
MUx. Следовательно: |
||||
|
ΔY |
|
MUx |
MRS XY . |
|
|
|
|
|
|
|
|
ΔX |
|
MUY |
|
|
|
|
|
|
||
Предельная норма замещения Y на X может рассматриваться как отношение предельной полезности Х к предельной полезности Y.

Бюджет даёт информацию о том, какое количество денег доступно для расходования в данный период, такой, например, как неделя. Это количество является доходом человека. Сколько товаров можно купить на этот доход зависит от цены товара.
Доход потребителя и покупательная сила денег определяют бюджетное ограничение. Бюджетное ограничение обусловливает выбор тех комбинаций благ, которые потребитель может позволить себе купить на свой доход.
Предположим, что потребитель тратит весь свой доход на товары Х и Y. Размер расходов на товары Х и Y должен равняться доходу потребителя.
Бюджетное ограничение можно записать в виде формулы:
I = РХ X + PY Y,
где I – доход, Px – цена товара Х, PY – цена товара Y.
Итак, бюджетное ограничение имеет смысл: доход потребителя равен сумме расходов на покупку товаров Х и Y.
Из уравнения бюджетного ограничения можно вывести уравнение бюджетной линии. Бюджетная линия показывает максимальное число комбинаций благ, которые потребитель может себе позволить при фиксированном доходе и ценах, которые он должен заплатить.
Преобразуя формулу бюджетного ограничения, мы получим уравнение бюджетной линии.
Y |
I |
|
PX |
X ; |
X |
I |
|
PY |
Y . |
PY |
|
PY |
PX |
|
PX |
||||
|
|
|
|
|
|
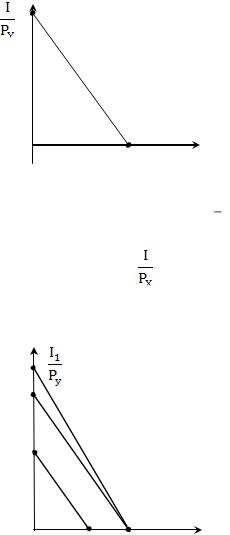
Точки пересечения бюджетной линии с осями
Y |
|
|
|
|
координат |
можно |
получить |
следующим образом: |
||||||||||
|
|
|
|
|
||||||||||||||
A |
|
|
|
|
если |
потребитель |
весь свой |
доход |
I тратит на |
|||||||||
|
|
|
|
|
||||||||||||||
|
|
|
|
|
покупку товара Х, |
то он сможет приобрести |
I |
|||||||||||
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
PX |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
единиц этого товара, поэтому длина отрезка ОВ |
|||||||||||||
|
|
|
|
|
равна |
|
I ; |
аналогично можно показать, что длина |
||||||||||
|
|
B |
X |
|
PX |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
отрезка ОА |
- |
I |
. Наклон бюджетной линии равен |
||||||||||
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
P |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Y |
|
|
|
|
|
|
|
|
|
|
|
|
PX |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
PY .. |
|
|
|
|
|
|
|
|
||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рисунок 4.12 – Бюджетная |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
линия |
|
|
|
|
|
Как изменится положение бюджетной линии при |
||||||||||||
А11 |
|
|
|
|
изменении дохода или цены товара? |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|||||||||||
А |
|
|
|
|
|
|
|
Допустим сначала, что доход |
потребителя |
|||||||||
|
|
|
|
уменьшился (I1< I), цены на товар при этом останутся |
||||||||||||||
|
|
|
|
|
||||||||||||||
|
|
|
|
|
неизменными. Наклон бюджетной линии не |
|||||||||||||
|
|
|
|
|
изменится, |
|
поскольку |
он |
определяется |
|||||||||
А1 |
|
|
|
|
соотношением цен. Следовательно, произойдёт |
|||||||||||||
|
|
|
I |
|
параллельный сдвиг бюджетной линии вниз. Она |
|||||||||||||
|
|
|
PX |
займёт положение (А1В1). При увеличении дохода и |
||||||||||||||
|
|
|
|
|
неизменных ценах будет наблюдаться параллельный |
|||||||||||||
0 |
В1 |
В |
сдвиг бюджетной |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Рисунок 4.13 – Сдвиги
линии вверх (рисунок 4.13).
бюджетной линии
Предположим, что доход и цена товара Х неизменны, цена же товара Y понизилась. Очевидно, что в этом случае точка В не изменит своего положения, а точка А займёт положение А1. Цель рационального потребителя состоит в максимизации полезности, получаемой от набора благ при заданном
бюджетном ограничении: max U(X, У) при Рх∙Х + Ру∙У = I. Рассмотрим решение
Х,У
этой проблемы графически.
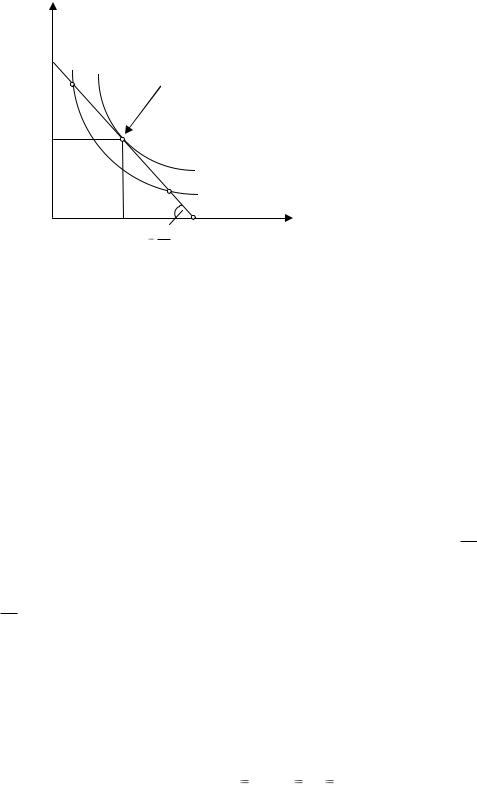
У
Точка внутреннего
U1 |
U2 |
оптимума |
|
a |
|
|
|
|
|
|
|
A |
|
E |
|
|
|
|
|
|
|
b |
|
0 |
Х* |
PX В |
Х |
|
|
PY |
|
Рисунок 4.14 – Выбор потребителем
оптимального выбора: максимизация
На рисунке 4.14 изображены две кривые безразличия U1, U2 и бюджетная линия АВ. Возможны две ситуации – бюджетная линия пересекает кривую безразличия U1 или касается кривой безразличия U2. На бюджетной линии АВ отмечены три набора благ: a, b, E. Расходы на их приобретение одинаковы и равны доходу потребителя. Рациональный потребитель сделает оптимальный выбор, чтобы на свой доход получить максимальную полезность.
Наборы a и b расположены на кривой безразличия U1, набор Е – на кривой безразличия U2. Учитывая, что U2 >U1, потребитель выберет набор Е. Таким образом, при заданном бюджетном ограничении оптимальный потребительский набор (Х*, У*) расположен в точке касания бюджетной линии и кривой безразличия. В точке Е наклон бюджетной линии и кривой безразличия
совпадают (напомним, что наклон бюджетной линии равен PX , наклон кривой
PY
безразличия равен MRSху.). Поэтому в точке оптимума выполняется равенство
PX = MRSху.
PY
Результат очень важен: удовлетворение максимизируется, когда предельная норма замещения У на Х равна соотношению цен Х и У.
Равенство |
PX |
|
= MRSху |
в порядковой теории полезности имеет такой же |
||||||||
|
||||||||||||
|
PY |
|
|
|
|
|
|
|
|
|||
смысл, что и |
равенство MUA |
MUB |
|
MU N в количественной теории. |
||||||||
|
|
|
|
|
PA |
|
|
PB |
PN |
|
||
|
|
|
|
|
|
|
||||||
Действительно, |
PX |
= MRSху |
= |
MU X |
. |
|
|
|
||||
|
|
|
|
|||||||||
|
PY |
|
MU Y |
|
|
|
|
|
||||
Это значит, что отношение рыночных цен благ характеризует их норму замещения на рынке, отношение предельных полезностей – индивидуальную
норму замещения. При их равенстве потребитель получает максимальную полезность при заданном доходе и рыночных ценах благ. Из формулы взвешенной предельной полезности имеем
MUX |
|
Px |
или |
MUX |
|
MUУ |
. |
|
|
|
|
|
|||
MUY |
|
Pу |
|
РХ |
|
РУ |
|
Потребитель достигает оптимального положения равновесия, если отношение предельных полезностей благ равно отношению их рыночных цен.
Потребитель рационально использует свой денежный доход, если последняя денежная единица (рубль, доллар и т.п.), затраченная на покупку любого блага, входящего в потребительский набор, приносит ему одинаковую полезность. В этом случае у потребителя отсутствует необходимость изменения структуры набора, и этот набор – оптимальный.
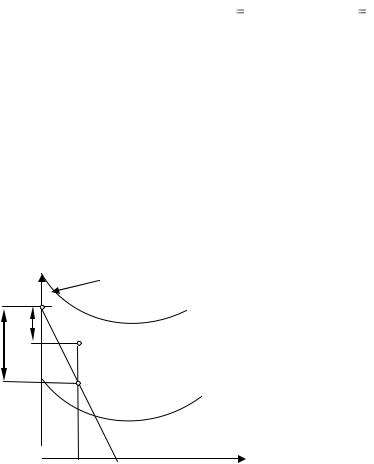
Y
Точка углового оптимума
Рисунок 4.15 – Угловое равновесие
В ординалистской модели потребительского выбора различают оптимум потребителя внутренний и угловой (внутреннее и угловое равновесие).
Внутренний оптимум полагает покупку обоих товаров Х и У, как на рисунке 4.14. Угловой оптимум означает, что один из товаров не потребляется вообще.
Угловое равновесие имеет место на одной из осей, в вершине угла, образуемого бюджетной линией (рисунок 4.15). В ситуации углового оптимума предельная норма замещения товаров не равна отношению цен. Это означает, что требования со стороны рынка к замещению товаров в определённой пропорции не совпадает с желанием потребителя замещать товары в этой же пропорции. Форма кривых безразличия, а также величина предельной нормы замещения благ MRSху зависит от характера потребительских предпочтений. Стандартные кривые имеют вид выпуклых к началу координат линий с отрицательным наклоном.
Рассмотрим нестандартные ситуации в формировании потребительских предпочтений.
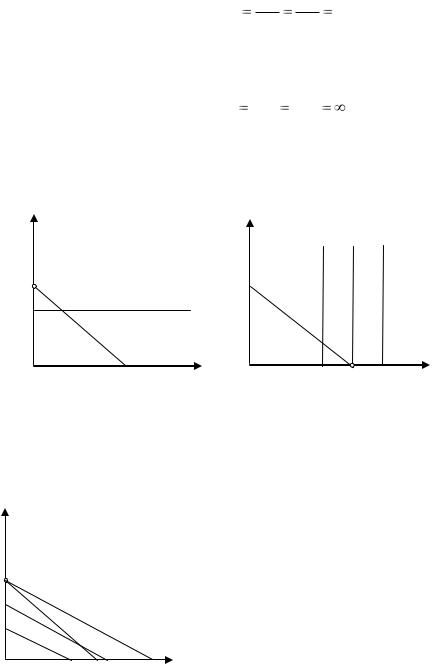
1. Абсолютное предпочтение товара. Такая ситуация имеет место, когда потребитель достиг полного насыщения другим товаром. В этом случае кривые безразличия вырождаются в прямые линии с предельной нормой замещения, равной нулю или бесконечности.
Если потребитель достигает полного насыщения товаром Х и потому не желает замещать товар У товаром Х, то (рисунок 4.16).
У 0 MRSХУ Х Х 0.
Если наоборот – достиг полного насыщения товаром У, то (рисунок 4.16)
MRSХУ |
У |
|
У |
. |
|
|
|
|
|||
Х |
0 |
||||
|
|
||||
В обоих случаях потребитель будет находиться в угловом равновесии, расходуя свой бюджет на покупку одного товара.
У |
а) |
У |
б) |
|
|
||
|
|
|
|
|
|
|
|
0 |
Х |
0 |
Х0 |
Х |
Рисунок 4.16 |
– Абсолютное предпочтение: а) товар Х; б) товар У. |
|||
2. Абсолютное замещение товаров. Такая ситуация возникает, когда потребитель рассматривает товары Х и У как идентичные.
У
0 |
– |
Х |
Рисунок 4.17 |
Абсолютное |
замещение товаров
Кривые безразличия в этом случае имеют форму прямых линий с постоянной нормой замещения MRS = a, 0<a<∞. Если на товары Х и У установлены разные цены, то потребитель будет покупать тот из них, который дешевле. При этом он будет находиться в состоянии углового оптимума. Такие потребительские решения типичны, например, для рынков лекарственных препаратов.
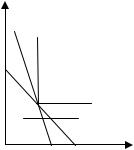
3. Абсолютная дополняемость товаров – |
это ситуация, когда разные товары |
|||||||
У |
|
могут |
потребляться |
только |
вместе в |
|||
|
|
|
некоторой |
фиксированной |
пропорции. |
|||
|
|
|
Например, левый и правый ботинок. |
|||||
|
|
|
||||||
|
|
Х |
Кривые |
|
безразличия |
имеют |
форму |
|
|
|
|
|
|
900 прямых |
|
||
|
|
X |
ломанных |
под углом |
линий. |
|||
0 |
|
Решения потребителя о покупке двух |
||||||
|
|
|||||||
|
|
|
||||||
Рисунок 4.18 – |
Абсолютное |
абсолютно |
дополняющих |
друг |
друга |
|||
|
|
|
|
|
|
|||
дополнение товаров |
товаров не зависит от соотношения их цен, |
|
|
|
его решение зависит от совокупной |
стоимости этих товаров. |
|
4.3. Реакция потребителя на изменение цены товара и дохода потребителя
Изменение цены. Пусть структура предпочтений потребителя, его доход, цена товара У останутся неизменными, а изменится лишь цена товара Х. Изменение цены товара Х, как нам уже известно, приведёт к изменению наклона бюджетной линии.
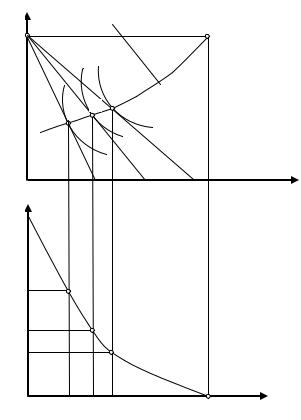
Допустим, что цена на Х снижается от р1х до р2х и далее до р3х . Бюджетная линия в этом случае будет разворачиваться против часовой стрелки вокруг точки I. Покупатель теперь может приобрести больше товара Х, если израсходует на него весь свой доход (рисунок 4.19). В то же время ему становятся доступными более удалённые от начала координат кривые безразличия. Оптимум
потребителя смещается из точки 1 в точку 2.
У |
|
Кривая «цена |
|
|
|
|
|
|
N
I
3
2
1
Х1 Х2 Х3 |
Х, ед. |
|
|
0 |
Х1 Х2 Х3 |
Х, ед. |
|
|
Рисунок 4.20 – Реакция потребителя на
Соединим точки оптимума потребителя 1, 2, 3 линией, которую будем называть кривой
«цена-потребление». Эта кривая предполагает множество всех оптимальных комбинаций товаров Х и У при изменении цены товара
Х.
На основе кривой «цена – потребление» можно постро-ить кривую индивидуального спроса
на товар Х, которая ставит в соответствие каждой цене товара Х оптимальный объём его потребления.
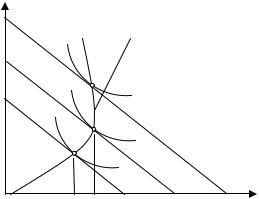
Изменение дохода. Если меняется только доход (цены и предпочтения неизменны), то на графике это выразится в параллельном сдвиге бюджетной линии. В случае увеличения дохода она отодвинется от начала координат и потребителю
|
|
|
|
|
|
|
|
|
|
|
|
|
станут |
доступны |
более высокие |
|||
У, руб. |
|
|
|
|
|
|
|
|
|
кривые безразличия, а в случае |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
уменьшения – приблизится к началу |
||||||
|
|
|
|
|
|
|
|
|
|
|
Кривая «доход - |
|
||||||
I2 |
|
|
|
|
|
|
|
|
|
координат и потребителю придётся |
||||||||
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
перейти |
на |
кривую безразличия с |
|||
|
|
|
|
|
|
3 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
меньшим |
уровнем |
полезности |
|||
I* |
|
|
|
|
|
|
|
|
|
Каждому |
уровню |
бюджета |
||||||
2 |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
потребителя. |
|
соответствует |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
некоторый |
|
оптимальный |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
Х1 |
Х2 |
|
|
|
|
Х, ед. |
потребительский |
набор. |
Соединим |
||||||
Рисунок 4. 21 – Реакция потребителя на |
||||||||||||||||||
точки оптимума потребителя 1, 2, 3 , |
||||||||||||||||||
изменение дохода. |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
получим кривую, названную Дж. |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Хиксом «доход – |
потребление». В экономической литературе она также получила |
|||||||||||||||||
название кривой уровня жизни. |
|
|
|
|
|
|||||||||||||
Кривая «доход – потребление» позволяет построить индивидуаль-ную кривую потребления Энгеля, которая показывает зависимость потребления тех или иных групп товаров от изменения доходов.Уже в XIX в. было замечено, что с ростом реального дохода потребителя потребление вторичных благ возрастает быстрее, чем предметов первой необходимости. Первым исследователем влияния изменения дохода на структуру потребительских расходов был немецкий статистик
Эрнест Энгель (1821– 1896). Он сформулировал закон потребления, который экономисты назвали его именем. Смысл закона состоит в том, что доля
национального дохода, израсходованного на продукты питания, является хорошим показателем уровня благосостояния. Чем ниже эта доля, тем выше благосостояние населения страны.
Для нормальных товаров кривая Энгеля имеет положительный наклон, т.к. с ростом дохода потребители покупают большее количество этих товаров (рисунок 4.22а). Для ряда товаров, называемых «низшими» или «низкокачественными», кривая Энгеля имеет отрицательный наклон. Этот термин означает, что с ростом доходов потребители уменьшают потребление этих товаров (рисунок 4.22б).

Следует отметить, что среди нормальных товаров можно выделить группу высококачественных товаров. К этой группе относятся товары, расходы на которые не просто растут с ростом дохода, а растут быстрее, чем рост дохода. В этом случае кривая Энгеля выглядит, как это показано на рисунке 4.22в.
И наконец, существует группа товаров, потребление которых остаётся постоянным при всех уровнях дохода. К ним относятся товары, расходы на которые занимают сравнительно небольшую часть бюджета, или те, которые рассматриваются как товары первой необходимости. Кривая Энгеля для таких товаров будет представлять собой горизонтальную линию (рисунок 4. 22г).
расходы |
|
|
расходы |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
расходы |
|
|
|
расходы |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
I1 |
I2доход |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
I1 |
I2 доход |
|
|
0 |
|
I1 |
I2доход |
|
|
0 |
I1 |
I2доход |
|||||
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рисунок 4. 22 – Кривые Энгеля: а) нормальный товар; б) низший товар;
Контрольные вопросы
1.На каких гипотезах основывается теория потребительского выбора? Объясните, что означают суверенитет потребителя, функция полезности и рациональное поведение потребителя.
2.Раскройте содержание первого и второго законов Госсена (кардиналистского определения функции полезности и критерия оптимума потребителя).
3.Как задаётся функция полезности в ординалистской теории потребительского выбора?
4.Раскройте содержание базовых аксиом ординалистского подхода. Дайте теоретическое толкование кривым безразличия. Какими свойствами обладают кривые безразличия?
5.Каков критерий оптимума потребителя в ординалистской модели. Объясните различие между внутренним и угловым равновесием потребителя.
6.Опишите, используя ординалистскую модель потребительского выбора (кривые
безразличия и бюджетные линии), реакцию потребителя на изменение его денежного дохода и цены товара.
Глава 5. Производство и издержки 5.1. Понятие производства. Технология и производственная функция. Изокванты
Изучение производства является первым шагом в формировании теории поведения производителя. Производство – это процесс использования рабочей силы и оборудования в сочетании с природными ресурсами и материалами для изготовления товаров и услуг. Продуктом производства являются товары и услуги. Институциональным образованием рыночной экономики является фирма, она предназначена для координации решений владельцев производственных ресурсов. Основу развития теории фирмы даёт предположение о том, что фирма максимизирует свою прибыль.
Решения фирмы относительно предложения того или иного количества продукции на рынке, а также спроса на факторы производства зависят от технологии, используемой фирмой.
Технология – это определённый способ преобразования |
факторов |
производства в едином производственном процессе. |
|
Методологически теория производства похожа на теорию потребления, с тем отличием, что основные её категории имеют не субъективнопсихологическую основу, а объективную природу.
Наиболее общим способом описания технологической стороны производства является производственная функция.
Производственная функция выражает зависимость между максимально возможным количеством продукции, произведённым в течение определённого периода времени, с одной стороны, количеством применённых фирмой ресурсов и технологией, с другой стороны:
Q = Q (K, L, ).
Экономический выбор фирмы зависит от соотношения цен экономических ресурсов и влияет на технологический выбор.
В теории производства традиционно используется двухфакторная производственная функция, которая даёт возможность графического анализа
производства. Если производственной функцией учитывается более чем два фактора производства, то требуется применение математического анализа. Двухфакторная производственная функция имеет вид
Q = f (L; К).
Теория производства строится на утверждении о том, что предприятия ведут себя рационально, т.е. стремятся к максимальной для себя прибыли. Если принять данное утверждение, то правомерно считать что предприятия должны выбирать такие технологические решения, которые обеспечивают выпуск продукта с наименьшими затратами ресурсов.
Эффективные по этому признаку производственные решения находятся на границе технологического множества. Границу технологического множества принято называть изоквантой.
Изокванта – это линия равного выпуска, отражающая различные комбинации ресурсов, которые могут быть использованы для производства данного объёма продукции. Изокванту можно показать графически.
Изокванты схожи по определению с кривыми безразличия, рассмотренными в теории потребления. Так же как кривые безразличия отражают альтернативные варианты потребительского выбора продуктов, обеспечивающие определённый уровень полезности, изокванты отражают альтернативные варианты затрат ресурсов для производства определённого объёма продукции. Они имеют следующие свойства:
изокванты не могут пересекаться, так как являются геометрическим местом равных выпусков продукции;
изокванты строго выпуклы к началу координат и имеют отрицательный наклон;
чем выше и правее расположена изокванта, тем больший объём выпуска она характеризует.
В отличие от кривых безразличия, где суммарное удовлетворение потребителей точно измерить нельзя, изокванты показывают реальные уровни производства (400, 600, 1200). Совокупность изоквант называется картой изоквант.
Отрицательный наклон изоквант объясняется тем, что увеличение использования одного фактора при определённом объеме выпуска продукта всегда сопровождается уменьшением количества другого фактора.
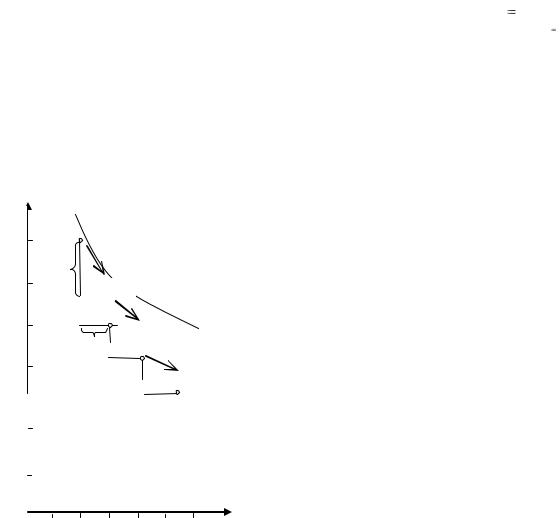
Производственная функция позволяет выстроить систему показателей, характеризующих различные стороны производительного процесса. Одним из таких показателей является предельная норма технологического замещения.
Предельная норма технологического замещения (MRTSLK – marginal rate of technical substitution) показывает, на какую величину требуется уменьшить затраты одного ресурса (капитала), чтобы увеличить затраты другого ресурса
(труда), сохраняя объём производства на прежнем уровне: MRTS LR |
ΔK |
. |
|
|
|||
ΔLQ const |
|||
|
|
Если фирма замещает капитал трудом, то она переходит от капиталоёмких к трудоёмким способам производства (рисунок 5. 1). Для увеличения труда на одну единицу она должна уменьшить капитал на 2 ед. (участок ab изокванты), 1 ед. (участок bс), 0,5 единиц (участок сd). Соответственно MRTSLK = 2; 1; 0,5, т.е. она равна наклону (по абсолютной величине) изокванты на этих участках.
К 60 |
а |
50 ∆К= -20 |
|
b
При достаточно малых изменениях ∆L и ∆К предельная норма технического замещения равна наклону касательной линии, проведённой к изокванте в этой точке. При движении сверху вниз вдоль
40 |
|
|
|
|
|
с |
|
кривой изокванты предельная норма |
|
|
|
|
|
|
|
|
|
||
|
|
|
∆L=10 |
|
|
|
|
технического замещения убывает. |
|
30 |
|
|
|
|
|
d |
|||
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
Изокванты (как и кривые безразличия) |
||
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
||
20 |
|
|
|
|
|
|
Q1200 |
||
|
|
|
|
|
|
имеют различную конфигурацию. |
|||
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
||
10 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
L |
|
10 |
20 |
30 |
40 |
50 |
60 |
||||
|
|
||||||||
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
Рисунок 5.1 – Убывание предельной нормы технического замещения капитала трудом
Если MRTSLK = const, то изокванты имеют форму прямых линий (рисунок 5.2а).
Если MRTSLK = 0, то изокванта имеет форму, предложенную на рисунке 5.2б. Если MRTSLK убывает, то изокванта имеет вид, как на рисунках 5.2 в, г.
