
5617
.pdf
и представляет собой средний период, в течение которого будет происходить изменение результата под воздействием изменения факторной переменной в момент времени t. Средний лаг измеряет скорость реакции y на изменение x. Небольшая его величина свидетельствует об относительно быстром реагировании результата на изменение факторной переменной, тогда как высокое его значение говорит о том, что такое воздействие будет сказываться в течение длительного периода времени.
Медианный лаг (lMe)– это величина лага, для которого
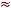 0,5.
0,5.
Это тот период времени, в течение которого с момента времени t будет реализована половина общего воздействия фактора на результат.
В общем случае оценить параметры уравнения модели с распределённым лагом методом наименьших квадратов представляется проблематичным. В этом случае оценке подлежат достаточно большое количество параметров в условиях мультиколлинеарности (лаговые переменные, как правило, тесно связаны друг с другом). Для решения этой проблемы обычно предполагаю, что известна структура лагов. Ш. Алмон (Almon S.) предложила считать, что зависимость величин коэффициентов такой модели от лагов является полиномиальной. В этом случае часть проблем, связанных с проблемами метода наименьших квадратов снимается.
Итак, будем считать, что коэффициенты модели с распределённым лагом
определяются из соотношений b |
j |
0 1 |
j |
2 |
j 2 ... |
k |
j k |
(полином от |
|
|
|
|
|
величины лага j степени к). Тогда после подстановки этих коэффициентов в исходное уравнение (после перегруппировки переменных) исходное уравнение можно заменить на уравнение от вспомогательных переменных с
коэффициентами |
i |
(эти преобразования предлагается провести |
|
|
самостоятельно). Вспомогательные переменные являются линейными комбинациями исходной независимой переменной и её лаговых значений с известными коэффициентами. Число вспомогательных переменных равно к (степени полинома), а поскольку это число, как правило, значительно меньше максимального лага (обычно не больше 4), то размерность вспомогательного уравнения будет существенно меньше размерности
51

исходного уравнения. Оценив вспомогательное уравнение, определим i , а
затем можно рассчитать значения коэффициентов исходного уравнения по приведённой формуле.
В EViews модель распределённых лагов рассчитывается несколько поиному, чем описывается в эконометрической литературе. Так, зависимость коэффициентов модели от лагов имеет вид
b |
j |
0 |
1 |
( j |
с) |
2 |
( j |
с)2 ... |
|
k |
( j с)k |
, (j = 0,1,2,…,l), |
|
|
|
|
|
|
k / 2, |
если |
к |
|
чётное |
|
|
где |
|
|
с = |
(k |
1) / 2, |
если |
к |
|
нечётное . |
|||
Введено это для того, чтобы уменьшить эффект мультиколлинеарности. На конечные результаты расчётов это введение влияния не оказывает.
При использовании метода Алмон необходимо предварительно решить две проблемы: определить максимальную величину лага и степень полинома. Обе проблемы решаются эмпирически.
При решении первой проблемы рекомендуется брать как можно большую величину лага, а потом на основании статистических критериев удалять последовательно незначимые слагаемые из уравнения модели. Аналогичные рекомендации действуют и в отношении определения степени полинома. А поскольку степень полинома, как правило, бывает не больше 4, то при компьютерных расчётах это не создаёт больших затруднений. Оценка параметров модели с распределёнными лагами реализована в большинстве статистических пакетов, и исследователю остаётся просчитать ряд вариантов и выбрать из них наиболее подходящий. Рассмотрим эту процедуру на примере эконометрического пакета EViews.
Чтобы задать в EViews расчёт модели с распределённым лагом, необходимо в спецификации уравнения регрессии задать (y с pdl(x,l,k)). Здесь у – зависимая переменная, с – константа, х – независимая переменная, l – максимальный лаг, к – степень полинома, pdl – polynomial distributed lag (полиномиально распределённый лаг). На рисунке 2.1 приведён отчёт об оценке модели pdl заданной спецификацией (y с pdl(x,5,1)), т.е. приведена оценка зависимости y от x с лагом, равным пяти годам, и степенью полинома, равной единице.
52

Рисунок 2.1 – Оценка параметров модели с распределённым лагом
Итак, в рассматриваемом примере уравнение с распределённым лагом в общем виде следующее:
yt = c + b0 xt + b1xt-1 + b2xt-2 + b3xt-3 + b4xt-4 + b5xt-5 + et.
Коэффициенты этого уравнения рассчитываются из соотношений bj=γ0+γ1(j-0,5) (полином 1-го порядка), (в нашем случае k=1 и c=k/2=0,5), а γ0 и γ1 определяются как оценки вспомогательного уравнения
yt = α + γ0 z0t + γ1 z1t,
где z0t и z1t – вспомогательные переменные, являющиеся линейными комбинациями текущих и лаговых значений независимой переменной.
На рисунке 2.1 с – это , PDLoj – это j (j=1,2), а коэффициенты bj
(j=0,1,2.3.4.5) – это числа в последней части отчёта в столбце Coefficient. Левее их помещён график распределения лагов.
Итак, в нашем примере уравнение регрессии с распределённым лагом имеет вид (с округлениями):
yt = 1,15 + 0,46xt + 0,35xt-1 + 0,24xt-2 + 0,13xt-3 + 0,02xt-4 – 0,09xt-5 + et.
В последней строке отчёта указан долгосрочный мультипликатор (Sum of Lags =1,11).
Отметим, что здесь найдено не лучшее уравнение регрессии. Свободный член уравнения с распределённым лагом незначим (Prob. для с равна 0,725), в остатках присутствует автокорреляция. Эти вопросы решаются отдельно и здесь не рассматриваются.
53

2.1.4. Уравнения модели с геометрически распределённым лагом (метод Койка)
Предположим, что величина лага не ограничена. Тогда модель с
распределённым лагом примет вид |
|
yt = c + b0xt + b1xt-1 + b2xt-2 + … + et. |
(2.8) |
Понятно, что параметры такой модели обычным методом наименьших квадратов определить нельзя, поскольку модель включает бесконечное их число. Один из методов решения задачи оценки параметров такой модели предложил Койк (Koyck L.M.). Он предложил считать, что структура лага имеет геометрическую форму, т.е. воздействие лаговых значений независимой переменной на результат уменьшается с увеличением величины лага в геометрической прогрессии. Итак, предположим, что существует некоторый постоянный темп λ (0 < λ < 1) уменьшения во времени лаговых воздействий факторной переменной на результат. В общем виде такую
зависимость можно записать как |
|
bj = b0 λj, j = 0,1,2,…, 0 < λ < 1. |
(2.9) |
Выразим с помощью (2.9) коэффициенты bj в модели (2.8) через b0 и λ:
yt = c + b0 xt + b0 λ xt-1 + b0 λ2 xt-2 + … + et. |
(2.10) |
Тогда для периода t–1 (2.10) можно записать следующим образом:
yt-1 = c + b0 xt-1 + b0 λ xt-2 + b0 λ2 xt-3 + … + et-1. |
(2.11) |
Умножим обе части (2.11) на λ и вычтем результат из (2.10), получим
yt – λ yt-1 = с – λ с + b0 xt + et – λ et-1
или
yt = с (1 – λ) + b0 xt + λ yt-1 + ut,
где
ut = et – λ et-1.
Получили модель авторегрессии первого порядка. Оценив параметры этой модели, получим оценки λ, b0 и с, после чего по формуле (2.9) получим оценки модели (2.8). Их количество определяется точностью оценок.
Отметим, что оценки модели авторегрессии первого порядка рекомендуется проводить методом инструментальных переменных ввиду наличия в ней в правой части лаговой зависимой переменной. Описанный алгоритм получил название преобразования Койка. Несмотря на бесконечное число слагаемых в правой части модели (2.8), геометрическая структура лага позволяет определить величины среднего и медианного лагов в модели
54

Койка. Средний лаг определяется из соотношения 
 λ/(1– λ), а медианный равен λme = (ln0,5)/ln λ.
λ/(1– λ), а медианный равен λme = (ln0,5)/ln λ.
2.2. Динамические модели с нестационарными переменными
2.2.1. Ложная регрессия
Предположение стационарности временных рядов является решающим для применения стандартных процедур оценивания и проверки гипотез. При этом используется тот факт, что выборочные дисперсии и ковариации конечны для любого объёма выборки. Но если ряды нестационарны, то они не вариируют вокруг постоянного среднего значения, а следовательно, дисперсии и ковариации для генеральной совокупности не определены.
Если моделируемые временные ряды нестационарны, то велика вероятность получить ложную регрессию, особенно, если эти ряды имеют тренды. Если взять два независимых временных ряда, которые имеют тренды, то уравнение регрессии для них просто отразит тот факт, что они изменяются в одном или противоположном направлении. Такая регрессия будет иметь хорошие показатели точности, но будет отражать лишь факт ложной связанности благодаря тому, что оба ряда имеют тренд. При этом ситуации будут совершенно разными, имеют ли ряды детерминированные или стохастические тренды.
Рассмотрим оба варианта. Сначала рассмотрим вариант с детерминированными трендами.
Смоделируем два временных ряда с детерминированными трендами и независимыми друг от друга остатками в виде белого шума (левая часть рисунка 2.2). Оценим уравнение регрессии yt на xt (правая часть этого рисунка). Как видим, уравнение регрессии вполне корректное: высокое значение коэффициента детерминации (0,98), значимое отличие от нуля оценок параметров уравнения, статистика Дарбина – Уотсона близка к двум. Кроме того, анализ остатков этой регрессии показал (рисунок 2.3), что они стационарны (автокорреляции нет и гипотеза о единичном корне отклоняется). Это всё из-за того, что оба ряда имеют детерминированные тренды и только.
55

Рисунок 2.26.6 – Пример ложной регрессии (детерминированные тренды)
Рисунок 2.3 Анализ остатков ложной регрессии
Чтобы убедиться в том, что эта регрессия действительно ложная, проделаем следующее: сначала введём в уравнение регрессии фактор времени в виде тренда, а потом проверим, объясняет ли изменение х изменение у, т.е. вместо уравнения yt = a +bxt + et (что на правой части рисунка 2.2) оценим уравнение yt = a +bxt +ct+ et (левая часть рисунка 2.4) и затем yt = a +b xt + et (правая часть этого рисунка).
56

Рисунок 2.4 – Преобразованные уравнения для случая ложной регрессии Как видим, точность уравнения с включением тренда по сравнению с исходным уравнением повысилась (R-squared = 0,99), остатки не автокоррелированы (DW = 1,89) (левая часть рисунка 2.4). Однако в уравнении регрессии с трендом оценка коэффициента при xt оказалась незначимой (Prob. = 0,38), зато при тренде – высокозначимой (Prob. = 0,00), т.е. в нашем случае yt зависит только от t и не зависит от xt. Это подтверждает ложность исходной регрессии. Кроме того, попытка объяснить зависимость изменения yt, т.е. yt от изменения xt, т.е. от xt, показала, что изменение xt не объясняет изменение yt (оценка коэффициента b в уравнении регрессии yt = a +b xt + et (правая часть рисунка 2.4) незначимо отличается от нуля (Prob. = 0,87)). Т.е. в этом случае также подтвердилась
ложность исходной регрессии.
Рассмотрим теперь вариант стохастических трендов. Смоделируем два независимых процесса случайного блуждания и построим уравнение регрессии одного ряда на другой (рисунок 2.5).
Рисунок 2.5 – Пример ложной регрессии (стохастические тренды)
57

Как и в предыдущем случае, уравнение зависимости y от x оказалось значимым (рисунок 2.5): F-статистика = 38, prob(F-statistic) = 0,00, оценки коэффициентов высокозначимы, R2 кажется приемлемым, а вот статистика Дарбина – Уотсона чрезвычайно низка, что говорит о высокой автокоррелированности остатков.
Протестируем остатки этой регрессии на стационарность с помощью теста Дики – Фуллера. На рисунке 2.6 (левая часть) приведены графики фактических, расчётных значений зависимой переменной и остатков уравнения регрессии (в центре левого рисунка) и тест на единичный корень (правая часть рисунка).
Рисунок 2.6 – Проверка остатков на единичный корень
Как видно из рисунка, остатки визуально представляют собой тот же процесс случайного блуждания, что и исходные ряды. Тест на единичный корень подтверждает этот вывод (Prob. = 0,08), т.е. гипотеза о единичном корне не отклоняется, следовательно, остатки являются нестационарным рядом. Это и подтверждает утверждение о том, что наша регрессия ложная.
Если оценить уравнение регрессии изменения одной из этих переменных на изменение другой, то получим тот же результат, что и в предыдущем случае (см. рисунок 2.7).
58

Рисунок 2.7 – Регрессия зависимости изменения у от изменения х
Как видим, изменение х не объясняет изменение у. Уравнение регрессии в целом незначимо и соответственно ничего не описывает.
Подведём итог. Если при детерминированных трендах в ложной регрессии остатки могут быть стационарными и проверка на ложную регрессию требует либо вводить в регрессию фактор времени, либо проверять, объясняют ли изменения одной переменной изменения другой, то при стохастических трендах в ложной регрессии остатки не являются стационарными и после установления этого факта дополнительной проверки не требуется.
2.2.2. Единичные корни и коинтеграция
Нестационарный процесс, первые разности которого стационарны, называется интегрированным процессом первого порядка и обозначается I(1). Стационарный процесс в этих обозначениях является I(0)-рядом. Как известно, при моделировании зависимости между временными рядами на основе регрессионного анализа важно знать, являются ли анализируемые ряды стационарными или нет. В случае стационарности оценки, полученные на основе метода наименьших квадратов, будут «хорошими», т.е. несмещёнными, эффективными и состоятельными. Но если моделируемые временные ряды не стационарны, велика вероятность получить ложную регрессию, особенно, если эти ряды имеют тренды. Отличить ложную регрессию от истинной можно, опираясь на теорию коинтеграции.
Предположим, что существует специфическое соотношение между двумя нестационарными временными рядами. Снова рассмотрим два случайных
59

блуждания yt и xt, но на этот раз предположим, что существует некоторое действительное линейное соотношение между ними. Существование этого соответствия отражается в утверждении, что существует некоторое значение β такое, что ряд yt – βxt является интегрируемым порядка 0, I(0), хотя оба ряда yt и xt являются интегрируемыми порядка 1, I(1). В этом случае говорят, что временные ряды yt и xt являются коинтегрированными. И хотя относящаяся к этому случаю теория оценивания нестандартна, можно показать, что состоятельное оценивание β в регрессии yt = α + βxt + εt возможно. В этом случае обычная оценка наименьших квадратов b является суперсостоятельной для β, поскольку она сходится к β намного быстрее, чем обычно. Поэтому обычные процедуры статистического вывода здесь не применимы.
Если yt и xt оба являются I(1) и существует β такое, что zt = yt – βxt является I(0), то yt и xt являются коинтегрированными, с β называемым коинтегрирующим параметром. В этом случае на долгосрочные динамические компоненты yt и xt действует особое ограничение. Т.к. оба временных ряда yt и xt являются I(1), они будут подчиняться «длинноволновым» компонентам, а zt, будучи I(0), нет: поэтому yt и βxt должны иметь долгосрочные динамические компоненты, которые фактически уравновешиваются, чтобы порождать zt.
Эта идея связана с понятием долгосрочного динамического равновесия. Предположим, что такое равновесие определяется соотношением yt = α + βxt. Тогда разность zt – α (где zt = yt – βxt) является «остатком равновесия», который измеряет величину отклонения значения yt от своего «значения равновесия» α – βxt. Если разность zt – α стационарна, то остаток равновесия стационарен и флуктуирует вокруг нуля. Следовательно, система в среднем будет находиться в равновесии. Однако, если yt и βxt некоинтегрированы и, следовательно, zt – α является I(1), остаток равновесия может долго блуждать, и пересечения нуля будут очень редкими. При таких обстоятельствах не имеет смысла рассматривать yt = α + βxt как долгосрочное динамическое равновесие. Следовательно, наличие коинтегрирующего параметра может интерпретироваться как наличие соотношения долгосрочного динамического равновесия.
Из рассмотренного следует, что важно различать случаи существования коинтегрирующего соотношения между yt и xt и случаи ложной регрессии.
60
