5617

В зависимости от принадлежности временного ряда к тому или иному классу различаются методы их анализа и прогнозирования. Прежде чем перейти к их рассмотрению, введём показатели точности прогноза.

1.3. Показатели точности прогноза

Любой прогноз несёт на себе определённую степень ошибки, поэтому при проведении прогнозов на основе той или иной модели исследователь всегда имеет дело со случайными отклонениями прогнозных значений от их реальных текущих и будущих значений. Такие отклонения в случае правильной спецификации модели предполагаются распределёнными нормально, а мерой их рассеяния вокруг прогнозных значений служат различные показатели точности прогноза.

Рассмотрим некоторые из них. Пусть yt – реальные значения показателей временного ряда, а ft – прогнозные. Тогда ошибка прогноза в период времени t составит:

et = yt – ft .

Средняя ошибка прогноза (МЕ) определится из соотношения

ME 1/n et

и характеризует степень смещённости прогноза. В идеальном случае МЕ 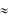0. Если прогнозные значения в среднем завышены, то МЕ < 0, а если занижены, то МЕ > 0.

Средний квадрат ошибки прогноза (MSE) определяется из соотношения

MSE 1/n et 2 .

Средняя абсолютная ошибка (МАЕ) вычисляется из соотношения:

MAE 1/n et .

MSE и МАЕ используются для сравнения процедур прогноза и подбора параметров сглаживания уровней элементов временного ряда.

Средняя абсолютная процентная ошибка (МРАЕ) вычисляется из соотношения:

МРАЕ 1/n et / yt 100

и используется для оценки качества прогноза.

Если МРАЕ < 10%, то считается, что точность прогноза высокая, при 10% < МРАЕ < 20% – хорошая, если 20% < МРАЕ < 50%, то точность

12

прогноза удовлетворительная и при МРАЕ > 50% – неудовлетворительная. МРАЕ вычисляется по ошибке прогноза на шаг вперёд.

Средняя процентная ошибка (МРЕ) вычисляется из соотношения:

МРЕ 1/n (et / yt ) 100

и служит показателем смещённости прогноза (не должна превышать 5%). Кроме того, в некоторых статистических пакетах прикладных программ

корень квадратный из MSE называется стандартной ошибкой и обозначается

RMSE.

Из разработанных и используемых в практике методов анализа временных рядов рассмотрим лишь несколько наиболее простых, часто используемых на практике и теоретически обоснованных.

1.4. Сглаживание уровней временных рядов

Этот метод анализа применяется в основном для выявления основной тенденции в развитии исследуемого явления и предназначен для устранения высокочастотных колебаний в уровнях временного ряда. Хотя с помощью этого метода можно устранить и сезонные колебания, выбрав в качестве интервала усреднения длину сезонности.

Среди множества различных вариантов этого метода наиболее простым является вычисление простой скользящей средней. При этом сначала выбирается длина интервала сглаживания и вычисленное значение средней арифметической на этом интервале в начале ряда присваивается его середине. Затем это действие сдвигается по уровням ряда на один элемент вправо и расчёты повторяются, т.е. вычисление средней арифметической как бы скользит по уровням ряда. Отсюда и название метода.

Данный метод наиболее эффективен при линейной динамике уровней ряда. В более общем случае используются методы взвешенной скользящей средней. Наиболее часто из них применяется метод экспоненциально взвешенной скользящей средней. В этом методе учитывается старение информации при удалении её от текущего момента времени.

Рассмотрим простую экспоненциально взвешенную среднюю. Пусть прогнозное значение для периода t рассчитывается по формуле

ft = yt + (1 - )yt-1 + (1 - )2 yt-2 +…+ (1 - )n yt- n + … ,

где – показатель, характеризующий вес текущего наблюдения, называемый параметром сглаживания (0 < < 1).

13

Теоретически здесь предполагается бесконечный временной ряд с коэффициентами при лаговых значениях уровней временного ряда, убывающих по экспоненте. В силу того, что 0 < < 1, коэффициенты-веса при соответствующих элементах временного ряда быстро убывают, и достаточно несколько первых слагаемых этой суммы, чтобы получить результат с достаточной точностью.

Преобразуем это выражение. Вынесем за скобку (1 - ):

ft = yt + (1 - )[ yt-1 + (1 - )yt-2 +…+ (1 - )n-1 yt-n + …].

В квадратных скобках получили значение для ft-1. Тогда можем записать: ft = yt + (1 - )ft-1. (1.1)

Тем самым мы получили модель экспоненциально взвешенной скользящей средней. Из (1.1) следует, что для того, чтобы вычислить экспоненциально взвешенную скользящую среднюю нет необходимости вычислять сумму длинного числового ряда, необходимо знать только значение уровня временного ряда в текущем периоде и экспоненциально взвешенную скользящую среднюю за предыдущий период.

Отметим, что сумма весов в выражении экспоненциально взвешенной средней (как сумма бесконечно убывающей геометрической прогрессии)

из них рассчитываются экспоненциально взвешенные средние и для нихт – ошибка прогноза, например, MSE. Минимальная ошибка и определит константу сглаживания. При расчётах на ЭВМ особых проблем при подборе не возникает ввиду автоматизации таких расчётов. Возможен и ручной вариант подбора значения этой константы.

После простого преобразования модели (1.1) экспоненциально взвешенные скользящие средние могут быть представлены в виде

ft = ft-1+ (yt - ft-1).

Данная форма представления модели оправдывает её название как адаптивной модели прогнозирования. По этой модели прогноз на очередной период t+1 равен предыдущему прогнозу плюс доля ошибки предыдущего прогноза, т.е. в модели учитываются результаты предыдущих прогнозов, т.е. прогноз на очередной период как бы адаптируется к результатам предыдущих прогнозов.

14

Есть разные рекомендации по выбору возможных значений , основная из них заключается в том, что при анализе стационарных временных рядов параметр сглаживания не должен выходить за пределы интервала 0,05 – 0,3. Считается, что если ошибка прогноза уменьшается при выходе значения за пределы указанного интервала, то это означает, что речь идёт о не стационарном временном ряде.

Следует отметить, что, как следует из (1.1), прогнозные значения при

более сглажены. Поэтому, когда по ходу решения задачи требуется повысить чувствительность прогноза к динамике исходных данных, то высокие значения вполне оправданы.

Отметим, что при расчётах по модели (1.1) встаёт проблема определения прогнозного значения на начальный период (при t = 1, т.е. f0). Обычно за f0 берут либо y1, либо среднее значение нескольких первых членов ряда. Как правило, на конечный результат расчётов выбор начального значения f0 практически не сказывается.

Приведём пример использования экспоненциально взвешенных скользящих средних. Рассмотрим (рисунок 1.7). Верхняя левая часть этого рисунка – это график исходного ряда, верхняя правая – экспоненциально

экспоненциально взвешенных скользящих средних.

Рисунок 1.7 – Экспоненциально взвешенные скользящие средние

15

1.5. Аналитическое выравнивание временных рядов

На практике часто приходится определять функциональную зависимость уровней временного ряда от времени. С этой целью сначала необходимо выполнить выравнивание уровней временного ряда, используя одну из возможных процедур, разработанных для этих целей. После этого вид динамики просматривается более чётко.

Процесс определения зависимости уровней временного ряда как функции от времени называется аналитическим выравниванием временных рядов. Обычно такую зависимость определяют, используя обычный метод наименьших квадратов, в котором в качестве независимой переменной выступает фактор времени. При таком подходе изменение исследуемого показателя связывают лишь с течением времени; считается, что влияние других факторов несущественно или косвенно сказывается через фактор времени.

Прогнозирование исследуемого показателя на перспективу при этом осуществляется на основе экстраполяции, т.е. на продление в будущее тенденции, наблюдавшейся в прошлом, путём подстановки в аналитически выраженную зависимость от времени значений будущих тактов времени. При этом к такой форме зависимости предъявляются все те требования, которые разработаны для классического регрессионного анализа.

Для иллюстрации применения аналитического выравнивания временного ряда рассмотрим рисунок 1.8, в котором изображены графики реального временного ряда, выравненный временной ряд по линейному тренду и график остатков уравнения тренда. Необходимо помнить, что на подобных графиках помещены две вертикальные оси координат: правая – для исходной информации, левая – для остатков.

На рисунке 1.9 приведены уравнение линейного тренда, показатели его точности и адекватности. Ясно, что данное уравнение тренда неадекватно отражает динамику временного ряда(статистика Дарбина-Уотсона близка к нулю), но пока цель определения адекватного тренда и не ставилась (здесь иллюстрируется сама идея аналитического определения уравнения тренда).

16

основан на проверке гипотезы о сохранении значений всех коэффициентов модели при переходе от одного подпериода полного периода наблюдений к другому. Другой вариант теста Чоу (на качество прогноза – Chow forecast test) сравнивает качество прогноза, сделанного на основе оценивания модели на одной части периода, с качеством прогноза, сделанного на основе оценивания модели на всём периоде наблюдений.

Рассмотрим первый вариант. Допустим, что тенденция ряда имеет нестабильную тенденцию. Это значит, что, начиная с некоторого момента времени t = n1, происходит изменение характера динамики изучаемого показателя, что приводит к изменению параметров тренда, описывающего эту динамику. Это означает, что момент времени n1 сопровождается значительными изменениями ряда факторов, оказывающих воздействие на изучаемый показатель. При этом весь ряд динамики будем считать выборкой, которую можно разделить на две подвыборки: до момента n1 и после момента n1. При проведении теста предполагается, что на подвыборках может быть достигнута однородность информации.

Для проверки гипотезы о том, что исходная выборка однородна и разбиение её на две части не приведёт к значимому изменению оценок моделей, оценённых на подвыборках, находят параметры трёх уравнений тренда. Первое уравнение строится для всей совокупности наблюдений, второе и третье – для соответствующих выделенных подмножеств совокупности наблюдений. Для каждого из этих уравнений находят остаточную сумму квадратов SSE = Σei2. Для общего уравнения обозначим её через SSE0, а для уравнений по подмножествам – через SSE1 и SSE2 соответственно. Тогда равенство SSE0 = SSE1 + SSE2 выполняется, если оценки параметров всех трёх трендов совпадают (совокупность однородная).

В противном случае SSE0 > SSE1 + SSE2 и чем больше разница между разными частями этого неравенства, тем больше различие между двумя подмножествами с точки зрения значения оценок параметров уравнений трендов. Существенность различия проверяют с помощью F-критерия. Его фактическое значение находят по формуле

,

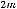
где m – число оцениваемых параметров уравнения тренда (без свободного члена), одинаковое для каждого уравнения. Если значение вычисленной статистики оказалось больше табличного (или, что всё равно, расчётный

18

уровень значимости оказался меньше принятого), то гипотеза об однородности отклоняется и считается, что имеют место структурные сдвиги и целесообразно строить уравнение тренда для каждого подмножества в отдельности.

Рассмотренный критерий может быть применён для тестирования однородности выборки (проверки стабильности модели) при разбиении всей выборки на несколько подвыборок. В этом случае при проведении расчётов, например в EViews, надо указать точки деления выборки на подвыборки и тест проверит, есть ли существенное различие в указанных подвыборках.

Идея критерия Чоу на качества прогноза сходна с рассмотренным методом. Но есть и различия. Рассмотрим его подробнее.

Сначала оцениваются параметры модели тренда и значения уровней элементов временного ряда по всей совокупности наблюдений. Затем совокупность наблюдений разбивается на две части: по первой части оцениваются параметры модели тренда и по оценённой таким образом модели прогнозируются уровни элементов временного ряда для второй части выборки. После этого проверяется, значимо ли различаются оценённые значения уровней ряда для второй части выборки по двум моделям. Если модель стабильна, то это различие не должно быть значимым. Степень различия измеряет статистика

F = ,

где n1 – объём первой части выборки;

SSE0 – остаточная сумма квадратов модели, оценённой по всей выборке; SSE1 – остаточная сумма квадратов модели, оценённой по первой части

выборки объёма n1.

Если модель стабильна, то указанная статистика имеет распределение Фишера и гипотеза о стабильности отклоняется, если вычисленное значение этой статистики превышает табличное значение при заданном уровне значимости (или, что то же, если расчётный уровень значимости окажется меньше принятого).

Проиллюстрируем работу теста Чоу на примере проверки гипотезы об отсутствии структурных изменений в значении переменной lnGDP (поквартальные данные), уравнение линейного тренда для которой приведено на рисунке 1.10.

19