
5617
.pdf
Критерий Шварца (Schwarz information criterion – SIC или BIC –
байесовский информационный критерий). При использовании этого критерия линейные модели с р объясняемыми переменными, оценёнными по n наблюдениям, сопоставляются по значениям
SIC = ln p2 + (lnn)p/n.
p2 + (lnn)p/n.
И здесь при увеличении количества оцениваемых параметров первое слагаемое уменьшается, а второе – увеличивается. Среди нескольких альтернативных моделей предпочтение отдаётся модели с наименьшим значением AIC.
Как видим, «штраф» в этом критерии больше, чем в предыдущем, поэтому он обычно и используется при выборе среди альтернативных моделей наилучшей.
Позднее для этих целей был предложен критерий Хеннана – Куинна
(Hannan – Quinn information criterion – HQC), который аналогичен рассмотренным, но более предпочтителен при больших объёмах выборки.
Важную роль в достижении успеха при построении модели играет личная оценка аналитика. Если две конкурирующие модели адекватно описывают данные, то проблему выбора можно решить только исходя из природы тех данных, для которых делается прогноз.
Этап 4. Прогнозирование на основе выбранной модели. Когда адекватная модель найдена, можно делать прогнозы на один или несколько периодов вперёд. На основе прогнозов строятся также интервалы предсказания. В общем случае, чем больше период прогнозирования, тем шире будет интервал предсказания. Обычно период прогнозирования рекомендуется брать не более трети длины исходного ряда.
Как только станут доступны новые данные наблюдений, ту же модель ARIMA можно применить для модифицированного прогноза, с новым началом отсчёта времени.
Если характер поведения ряда меняется, новые данные могут послужить для переоценки параметров модели или, если в этом есть необходимость, для разработки совершенно новой модели.
Хорошей идеей является постоянный мониторинг ошибки прогнозирования. Если амплитуда ошибок значительно возрастает со временем, то может потребоваться пересмотр используемой модели.
Проиллюстрируем работу рассмотренного метода на примере следующего временного ряда (рисунок 1.28).
41

Рисунок 1.28 – График анализируемого временного ряда
По графику (рисунок 1.28) видно, что ряд не стационарный, да и коррелограмма показывает (рисунок 1.29), что в уровнях ряда есть тренд (автокорреляции отличны от нуля и постепенно убывают).
Рисунок 1.29 – Коррелограмма анализируемого временного ряда
ADF-тест на единичный корень первых разностей (рисунок 1.30) показывает, что ряд первых разностей стационарный (Prob. =0.00).
42

Рисунок 1.30 – ADF-тест на единичный корень первых разностей
Будем строить модель для первых разностей. Коррелограмма первых разностей (рисунок 1.31) указывает на модель МА(1), около этой спецификации и будем искать адекватную модель.
Рисунок 1.31 – Коррелограмма первых разностей анализируемого ряда
Применим к рассматриваемому ряду метод Бокса – Дженкинса, перебирая различные варианты моделей авторегрессии – скользящего среднего для первых разностей. Начнём с модели ARIMA(1,1,0).
Спецификацию ARIMA(1,1,0)-модели в EViews можно задать командой
Equation eq1.ls d(x) c ma(1).
Получим следующий отчёт о решении задачи оценивания параметров этой модели (рисунок 1.32).
43
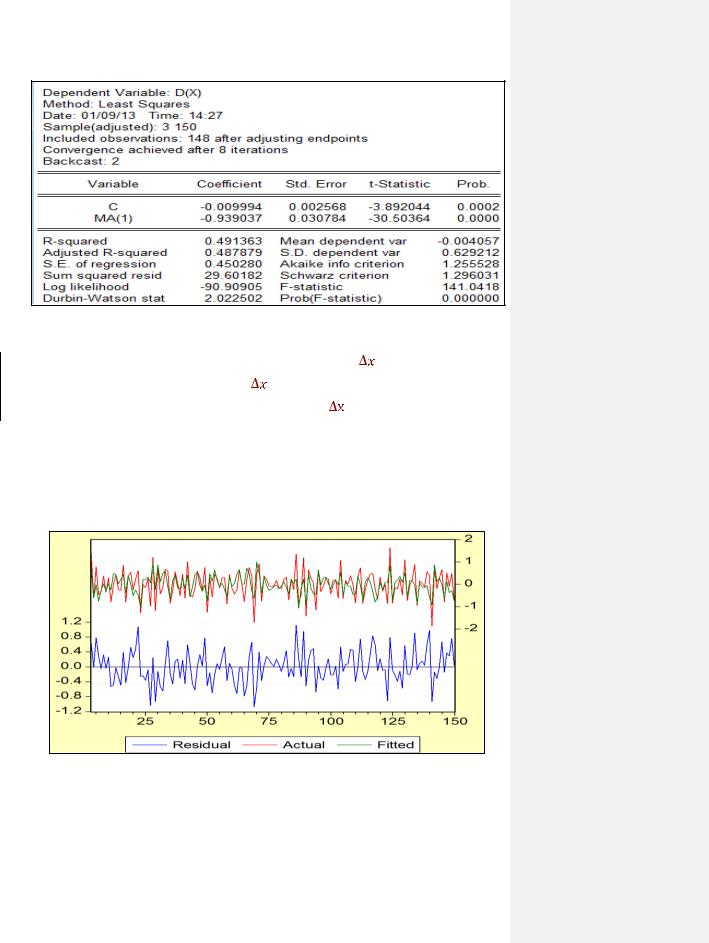
Рисунок 1.32 – Отчёт о решении задачи оценки параметров модели
На рисунке 1.32 – зависимая переменная D(X), т.е. |
, а независимые С и |
|||
МА(1), |
т.е. оценивается уравнение: |
= с + α |
εt-1. |
Получили следующие |
оценки: с = –0,01, α = –0,94 (с округлениями). Т.к. |
t = |
xt – xt-1, окончательно |
||
имеем |
xt = – 0,01+ xt-1 – 0,94 εt-1. |
|
|
|
Чтобы оценить адекватность модели, проанализируем остатки модели (рисунок 1.33). На этом рисунке показано: исходный график ряда (Actual), график смоделированного ряда (Fitted) и график остатков (Residual).
Рисунок 1.33 – График, характеризующий результаты расчётов по модели
По графику остатков можно сделать вывод, что модель адекватна (график остатков часто пересекает линию нуля и разброс остатков примерно одинаков на протяжении всего рассматриваемого периода), к тому же
44
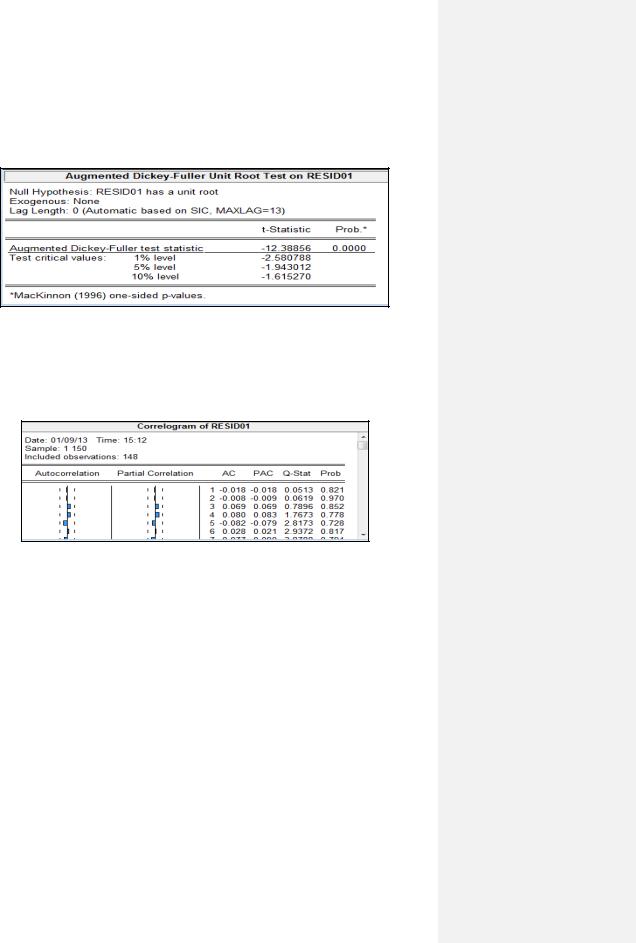
статистика Дарбина – Уотсона (рисунок 1.32) равна почти двум, что свидетельствует об отсутствии автокорреляции в остатках. Тем не менее протестируем остатки на единичный корень (рисунок 1.34).
Рисунок 1.34 – Тест на единичный корень в остатках модели
Гипотеза о единичном корне отклоняется (Prob. = 0,0), т.е. остатки – стационарный временной ряд.
Рисунок 1.35 – Коррелограмма остатков модели ARIMA(1,1,0)
Коррелограмма остатков модели (рисунок 1.35) показывает, что остатки являются белым шумом. При попытке изменить спецификацию модели (добавление других членов в модель) оказалось, что качество модели не изменилось. Так что в данном случае оценённую модель можно признать адекватной.
Глава 2. Многомерные модели временных рядов
До сих пор рассматривались модели для стохастического процесса единственного временного ряда. Но в экономической практике переменные, как правило, взаимосвязаны и значения одной из них могут помочь в прогнозировании значений другой. Поэтому более интересно рассматривать
45

одновременно несколько временных рядов. Кроме улучшения прогнозов, анализ нескольких временных рядов одновременно позволяет рассматривать вопросы «что если». Например, как изменятся расходы семьи при изменении доходов?
2.1.Динамические модели со стационарными переменными
Вэконометрическом анализе динамическими называют модели, в которых в правой части содержатся лаговые значения рассматриваемых переменных. Тем самым отражается динамика анализируемых показателей.
Рассмотрим две стационарные переменные yt и xt и предположим, что имеет место соотношение
yt = δ + α1 yt-1 + β0 xt + β1 xt-1 + εt. |
(2.1) |
Пусть это будут: yt – объёмы продаж компании, xt – затраты на рекламу в период t. Если предположить, что εt является процессом белого шума, независимым от регрессоров и их предыстории, то это соотношение называют авторегрессионной моделью распределённых лагов. Для состоятельной оценки параметров этой модели можно использовать обычный метод наименьших квадратов (все его предпосылки выполняются).
Рассмотрим описание текущих и будущих значений переменной yt в зависимости от динамических эффектов изменения в переменной xt. Взяв частные производные, получим, что непосредственный отклик в момент времени t задаётся в виде
yt/ xt = β0.
Этот отклик называют краткосрочным мультипликатором воздействия. Увеличение хt на единицу влечёт непосредственное изменение уt на β0 единиц.
Эффект после одного периода времени (в момент времени t+1) равен
yt+1/ |
xt =α1 |
yt/ xt + β1 = α1 β0 + β1, |
а после двух периодов |
|
|
yt+2/ |
xt = α1 |
yt+1/ xt = α1 (α1 β0 + β1) |
и т. д. Это показывает, что после первого периода эффект уменьшается, если |α1|<1. Как известно, это условие является требованием стационарности авторегрессионного процесса и позволяет определить долгосрочный динамический эффект единичного приращения xt. Этот эффект задаётся
46

долгосрочным динамическим мультипликатором (или мультипликатором равновесия). Просуммируем промежуточные мультипликаторы
β0 + (α1 β0 + β1) + α1 (α1 β0 + β1) + … = β0 + (α1 β0 + β1) (1+ α1 + α12 +… ) = = β0 + (α1 β0 + β1) /(1- α1) = (β0 + β1)/(1– α1).
Таким образом, если затраты на рекламу xt возрастут на единицу, то ожидаемое накопленное увеличение в объёмах продаж выражается в виде
(β0 + β1)/(1– α1).
Если возрастание xt является постоянным, то долгосрочный динамический мультипликатор имеет интерпретацию математического ожидания долгосрочного динамического постоянного возрастания yt. Из соотношения (2.1) в предположении стационарности рассматриваемых временных рядов (т.е. если M(yt) = M(yt-1) и M(xt) = M(xt-1) – математические ожидания не зависят от времени и M(εt) = 0) получим
M(yt) = δ + α1M(yt) + β0M(xt) + β1 M(xt)
или |
|
M(yt) = δ/(1– α1) +(β0 + β1)/(1– α1) M(xt). |
(2.2) |
что представляет альтернативный вывод долгосрочного динамического мультипликатора.
2.1.1. Модель коррекции остатков
Запишем альтернативный способ формулировки авторегрессионной модели распределённых лагов из выражения (2.1). Для начала запишем выражение (2.2) короче, введя обозначения α = δ/(1- α1), β = (β0 + β1)/(1- α1). Получим
M(yt) = α + β M(xt).
Преобразуем теперь выражение (2.1). Вычтем из обеих его частей yt-1 и в правой части добавим и вычтем β0 xt-1.
Получим
yt – yt-1 = δ + α1 yt-1 – yt-1 + β0 xt – β0 xt-1+ β0 xt-1 + β1 xt-1 + εt
или
yt = δ – (1– α1)yt-1 + β0 xt + (β0 + β1) xt-1 + εt |
|
или |
|
yt = β0 xt – (1– α1)[yt-1 – α – βxt-1]+ εt. |
(2.3) |
В квадратных скобках α и β соответствуют введённым обозначениям и выражение в них соответствует остатку равновесия yt = α + βxt в предыдущий
47

момент времени (t–1). Формулировка (2.3) является примером модели коррекции остатков. Согласно данной модели, приращение в переменной yt (т.е. yt) происходит из-за текущего приращения в переменной xt (т.е. xt) плюс член коррекции остатков. Если остаток равновесия в квадратных скобках положителен, то производится отрицательная дополнительная коррекция в переменной yt. Скорость коррекции определяется коэффициентом (1–α1), который является параметром коррекции. Предположение устойчивости гарантирует, что (1–α1) > 0. Модель коррекции остатков можно состоятельно оценить методом наименьших остатков. В обеих моделях (и в (2.1) и в (2.3)) предполагается, что значения xt рассматриваются как заданные, т.е. как не коррелированные с членами ошибок уравнений иначе оценки их параметров были бы несостоятельными. Причём, эти оценки для обеих моделей будут численно идентичны.
2.1.2. Модель частичного приспособления
Это следующий специальный случай модели (2.1). Обычно в экономике субъекты не сразу могут приспособиться к меняющимся условиям – это происходит постепенно и для этого нужно время. Такие процессы можно моделировать с помощью модели частичного приспособления или модели неполной корректировки.
Пусть yt* – (эмпирически ненаблюдаемый) оптимальный или желаемый уровень yt и предположим, что этот уровень зависит от реального значения переменной xt и эта зависимость описывается моделью
yt* = α + βxt +ηt, |
(2.4) |
где α и β – неизвестные параметры модели, а ηt – остаточный член,
независимый от xt |
и его лаговых значений. Фактическое значение yt |
отличается от yt* |
потому, что коррекция её оптимального уровня, |
соответствующая xt, не является мгновенной. Предположим, что коррекция является только частичной в том смысле, что
yt - yt-1 = (1– α1)(yt* – yt), |
(2.5) |
где 0 < α1 < 1. Коэффициент (1 – α1) называется корректирующим коэффициентом. Чем ближе его значение к 1, тем в большей степени реальная динамика анализируемого показателя отвечает ожидаемому оптимальному уровню и наоборот, чем ближе его значение к 0, тем менее его реальное изменение соответствует желаемому изменению.
48

Подставив в соотношение (2.5) выражение (2.4), получим
yt = yt-1 + (1– α1)α + (1– α1) β xt + (1– α1) yt-1 + (1– α1) ηt = δ + α1 yt-1 + β0 xt + εt,
где δ = (1– α1)α, β0 = (1– α1) β, εt =(1– α1) ηt. |
(2.6) |
Окончательно получили |
|
yt = δ + α1 yt-1 + β0 xt + εt. |
(2.7) |
Эта модель является частным случаем модели (2.1), поскольку не включает xt-1. Модель, заданная соотношениями (2.4) и (2.5), называется моделью частичного приспособления или неполной корректировки.
Параметры модели (2.4) (эта модель называется долгосрочной функцией модели неполной корректировки) непосредственно оценить не представляется возможным из-за того, что зависимая переменная в ней непосредственно не наблюдается. После преобразования получили уравнение модели (2.7) (эта модель называется краткосрочной функцией модели неполной корректировки), в которой все входящие в неё переменные наблюдаются непосредственно и параметры этой модели можно оценить методом наименьших квадратов, а после этого получить оценки и параметров модели (2.4), воспользовавшись (2.6).
Следует отметить, что при оценке параметров уравнения (2.7) (это уравнение авторегрессии первого порядка) обычным методом наименьших квадратов можно столкнуться с проблемой, связанной с нарушение предпосылки о независимости регрессоров и остатков, т.к. в правую часть этой модели входит лаговое значение зависимой переменной. Одним из методов решения этой проблемы является применение метода инструментальных переменных.
Рассмотрим ещё одну модификацию уравнения (2.1). Предположим, что в правой части этого уравнения отсутствует лаговое значение зависимой переменной, а независимая переменная присутствует с несколькими лагами. Такая модификация уравнения (2.1) называется уравнением модели с распределённым лагом.
Рассмотрим два варианта таких моделей – с конечной величиной максимального лага (полиномиальные лаги) и с бесконечной величиной лага (геометрические лаги).
49

2.1.3. Уравнения модели с полиномиально распределённым лагом (лаги Алмон)
Если в правой части уравнения (2.1) присутствует только независимая переменная со своими лаговыми значениями, то такое уравнение называется уравнением с распределённым лагом. Если максимальная величина лага ограничена (например, величиной l), то такое уравнение можно записать в виде
yt c b0 xt b1 xt 1 b2 xt 2 ... bl xt l et .
Эта модель говорит о том, что если в некоторый момент времени t происходит изменение независимой переменной x, то это изменение будет влиять на значения переменной y в течение l следующих моментов времени.
Коэффициент регрессии b0 при переменной xt характеризует среднее изменение yt при изменении xt на единицу своего измерения в некоторый фиксированный момент времени t. Этот коэффициент называют краткосрочным мультипликатором.
По аналогии с моделью (2.1) сумму всех промежуточных мультипликаторов назовём долгосрочным мультипликатором и определим как
b = b0 + b1 + … +bl.
Величина b показывает изменение в долгосрочном периоде t+1 результата y под влиянием изменения на единицу независимой переменной xt.
Введём понятие относительных коэффициентов модели с распределённым лагом
βj = bj/b, j = 0,1,2,…,l.
Эти коэффициенты показывают вклад отдельного лага в суммарное влияние всех лагов. Функция βj целого аргумента называется распределением лагов. Если все коэффициенты bj имеют одинаковые знаки, то для любого j
0 < βj < 1 и |
=1. |
В этом случае относительные коэффициенты βj являются весами для соответствующих коэффициентов bj. Каждый из них измеряет долю общего изменения результативного признака в момент времени t + j.
Зная величины βj, можно определить такие важные характеристики модели с распределённым лагомкак величины среднего лага и медианного лага. Средний лаг определяется по формуле
50
