Таблица 1

Вероятность того, что событие А в n испытаниях появится:

Для вычисления значений Pn(m) в Excel по формуле Бернулли используется функция БИНОМРАСП. Синтаксис этой функции имеет вид: БИНОМРАСП (число_успехов;число_испытаний; вероятность_успеха; интегральная). Здесь:

число_успехов – это количество испытаний, в которых появилось интересующее нас событие;

число_испытаний – число независимых испытаний; вероятность_успеха – вероятность появления события в каждом

отдельном испытании; аргумент интегральная – определяет форму функции. Если этот

аргумент имеет логическое значение истина (или равен 1), функция БИНОМРАСП вычисляет вероятность того, что число успешных испытаний окажется меньше или равно значению аргумента число_успехов. Если этот аргумент имеет значение ложь (или равен 0), функция БИНОМРАСП вычисляет вероятность того, что число успешных испытаний в точности равно значению аргумента число_успехов.

Пример 1

Известно, что в определённом городе 30% граждан предпочитают добираться на работу личным автотранспортом. Случайно отобраны восемь человек. Определить вероятность того, что из восьми респондентов используют автомобиль а) не более трех человек; б) ровно трое опрошенных.

Решение

Дано: n=8; p=0,3; q=1– p =0,7; а) m≤3; б) m=3.

1.Чтобы ответить на первый вопрос задачи, необходимо:

−устанавить табличный курсор в свободную ячейку, например в А1. Здесь должно оказаться значение искомой вероятности.

12

−для получения значения вероятности воспользуемся специальной функцией: нажимаем на панели инструментов кнопку

Вставка функции (fx).

−в появившемся диалоговом окне Мастер функций-шаг 1 из 2 в поле Категория указаны виды функций. Выбираем Статистическая. В поле Функция выбираем функцию БИНОМРАСП. Нажимаем на кнопку ОК.

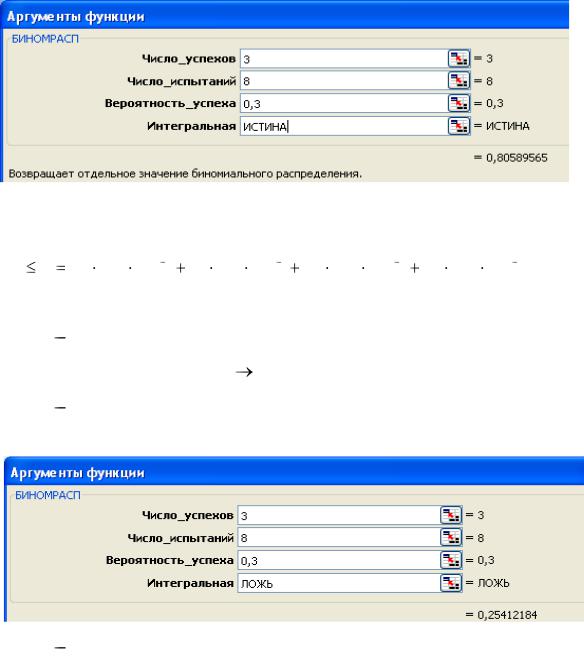
−в открывшемся диалоговом окне Аргументы функции заполнить поля в соответствии с рисунком, затем нажать кнопку ОК:

2. Для ответа на второй вопрос задачи необходимо:

установить курсор в ячейку А2, вызвать Мастера функций и

найти функцию БИНОМРАСП ОК;

воткрывшемся диалоговом окне Аргументы функции

заполнить поля в соответствии с рисунком, затем нажать кнопку ОК:

в результате получим значение вероятности р = 0,254122, что соответствует вычислению по формуле

13

P8 (m 3) C83 0,33 0,78 3 ≈ 0,254.

Таким образом, ровно 3 опрошенных из 8 предпочитают личный автотранспорт с вероятностью р = 0,254.

Для вычисления значений Pn(m) в Excel по формуле Пуассона используется функция ПУАССОН, которая имеет следующий синтаксис

ПУАССОН (х; среднее; интегральная). Здесь:

х – предполагаемое число наступления некоторого события; среднее – величина λ=np;

интегральная определяет тип возвращаемого результата. Если этот аргумент имеет значение истина (или равен 1), функция ПУАССОН возвращает интегральное распределение Пуассона, т.е. вероятность того, что число успешных испытаний окажется не больше значения аргумента х. Если аргумент Интегральная имеет значение ложь (или равен 0), функция ПУАССОН возвращает вероятность того, что число событий будет в точности х.

Пример 2

На предприятии 1 000 единиц оборудования определённого вида. Вероятность отказа единицы оборудования в течение часа составляет 0,003 и не зависит от состояния другого оборудования. Какова вероятность отказа а) двух единиц оборудования в час; б) не более двух единиц в час.

Решение

1. Для получения ответа на первый вопрос задачи:

активизировать ячейку А1, обратиться к Мастеру функций и найти функцию ПУАССОН ОК;

воткрывшемся диалоговом окне Аргументы функции

заполнить поля в соответствии с рисунком, затем нажать кнопку ОК

14

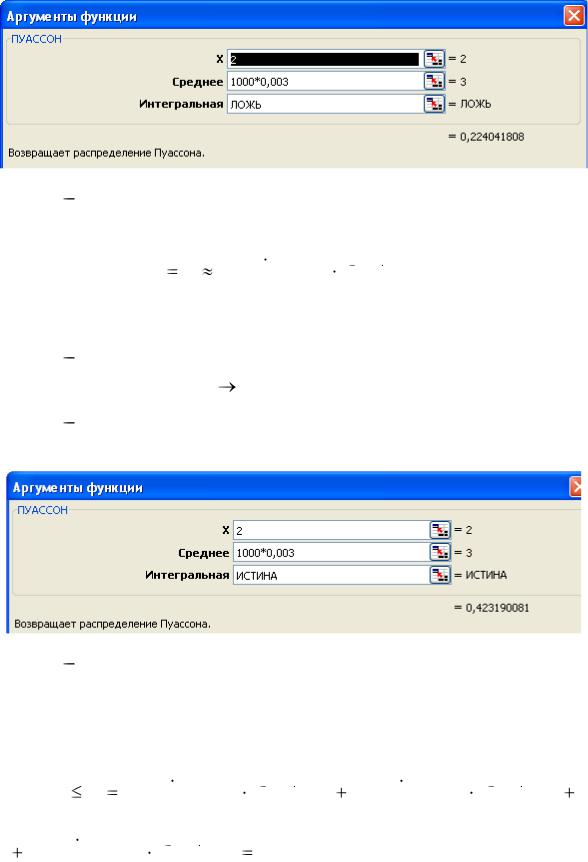
в результате получим значение вероятности отказа двух единиц оборудования в течение часа, что соответствует вычислению по формуле

2. Для получения ответа на второй вопрос задачи:

активизировать ячейку А2, обратиться к Мастеру функций и найти функцию ПУАССОН ОК;

воткрывшемся диалоговом окне Аргументы функции

заполнить поля в соответствии с рисунком, затем нажать кнопку ОК:

в результате получим значение вероятности выхода из строя не более двух единиц оборудования в течение часа, что соответствует вычислению по формуле

15

УПРАЖНЕНИЯ

1.Вероятность своевременной поставки продукции для каждого из пяти поставщиков постоянна и равна 0,7. Найти вероятность того, что своевременно поставят продукцию а) двое поставщиков; б) не более четырех поставщиков.

2.На 150 предприятиях края была произведена аудиторская проверка хозяйственной деятельности. Найти вероятность того, что у 50 предприятий были выявлены серьезные нарушения, если вероятность подобных нарушений для каждого объекта 0,3.

3.Вероятность производственной травмы в течение года равна 0,0005. Какова вероятность того, что из 10 000 рабочих пострадает 3 человека?

4.Вероятность того, что посетитель магазина совершит покупку, равна 0,5. Найти вероятность того, что из 8 посетителей покупку сделает: а) не более двух человек, б) не менее двух человек.

1.3.Случайная величина. Закон распределения случайной величины

Случайной называют величину, которая в результате испытания примет одно и только одно возможное значение, наперёд неизвестное и зависящее от случайных причин, которые заранее не могут быть учтены.

В зависимости от множества значений, принимаемых случайной величиной, выделяют дискретные и непрерывные случайные величины.

Дискретной случайной величиной (ДСВ) называется случайная величина, множество значений которой конечно или бесконечно, но счётно.

Непрерывной случайной величиной (НСВ) называется случайная величина, которая может принимать все значения из некоторого конечного или бесконечного промежутка.

Законом распределения случайной величины называется соответствие между её возможными значениями и вероятностями, с которыми она их принимает. Закон распределения можно задавать тремя способами.

16

1. Табличный.

Табличным способом можно задать только дискретную случайную величину. В этом случае первая строка таблицы содержит возможные значения, а вторая – их вероятности:

2. Графический.

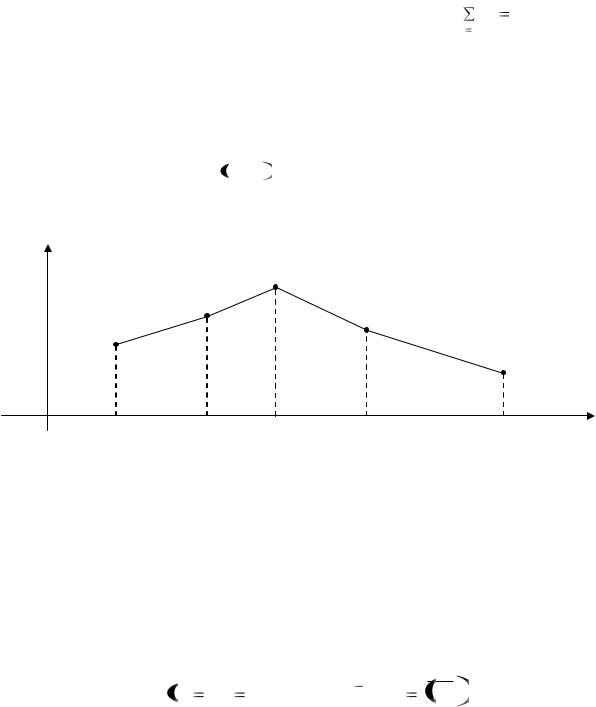
Для наглядности закон распределения дискретной случайной величины можно изобразить и графически, для чего в прямоугольной системе координат строят точки xi , pi , а затем соединяют их отрезками.

Полученную фигуру называют многоугольником распределения (рис. 1).

pn

Рис. 1

Для непрерывной случайной величины данный график будет представлять собой кривую распределения вероятностей.

3. Аналитический.

Закон распределения случайной величины можно задавать также формулой. Например, биномиальный закон распределения дискретных случайных величин задается формулой Бернулли:

Pn X m Cnm p m q n m , m 0, n .

Основные законы распределения дискретных случайных величин и их

Таблица 2

Основные законы распределения дискретных случайных величин

18

Пример

Контролёр проверяет на соответствие стандарту 8 изделий. Вероятность того, что каждое из изделий будет признано годным, равна 0,6. Составить закон распределения случайной величины Х – числа стандартных изделий среди проверенных. Найти числовые характеристики случайной величины Х. Построить многоугольник распределения вероятностей.

Решение

1. В диапазон А1:В3 внести исходные

вячейку А6 – pi.

3.В диапазон В5:J5 внести все возможные значения, которые может принять в результате опыта случайная величина Х – число стандартных изделий (от 0 до 8). При заполнении ячеек использовать средство

Автозаполнение.

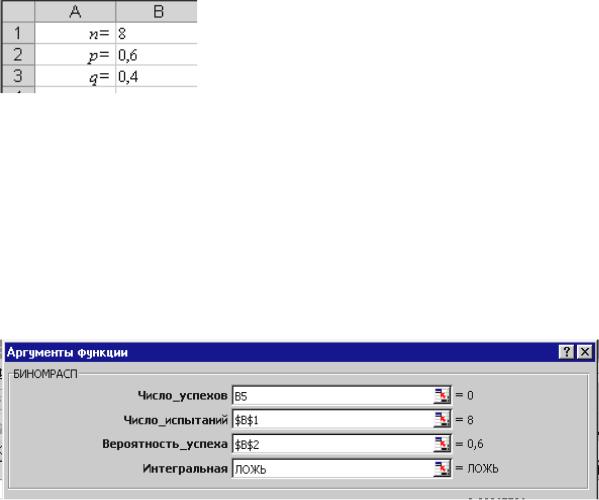
4.Установить курсор в ячейку В6, обратиться к Мастеру функций, найти функцию БИНОМРАСП и заполнить поля диалогового окна Аргументы функции в соответствии с рисунком, затем нажать кнопку ОК:

Обратите внимание, что ссылки на ячейки В1 и В2 должны быть абсолютными ($В$1; $В$2), в то время как ссылка на ячейку В5 – относительная. Это позволит скопировать формулу в диапазон ячеек

C6:J6.

19

5.Оформить составленный ряд распределения в виде таблицы (задать границы, отформатировать значения диапазона В6:J6 до трех цифр после запятой).

6.Проверить условие нормировки, установив курсор в ячейку D8 и выполнив суммирование диапазона В6:J6.

7.Рассчитать М(Х), D(X), σ(Х), делая ссылки на ячейки с соответствующими значениями.

8.Сравните полученный результат с образцом (формульный вариант):

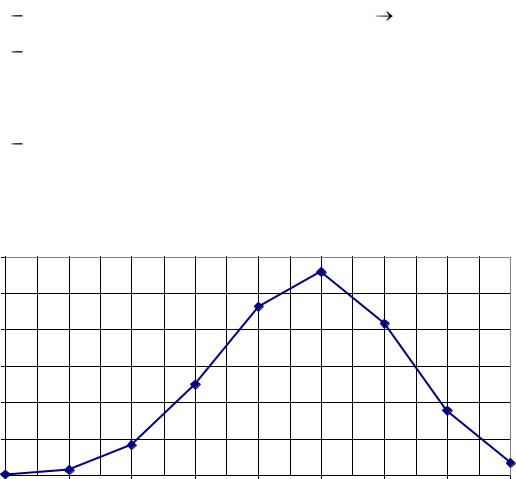
9. Для построения многоугольника распределения установить курсор в свободную ячейку (например, А13). Обратиться к мастеру диаграмм:

установить переключатель в позицию Ряды в строках. Установить курсор в поле Диапазон и выделить мышью диапазон В6:J6. Перейти на вкладку Ряд;

установить курсор в поле Подписи оси Х и выделить мышкой диапазон В5:J5 Далее;

на вкладке Заголовки ввести с клавиатуры название диаграммы, подписи осей; на вкладке Подписи данных поставить флажок в поле

Значения; на вкладке Легенда снять флажок в поле Добавить легенду. На вкладке Линии сетки установить флажок в позиции Ось Х:

промежуточные линии Далее;

20

УПРАЖНЕНИЯ

1. При передаче сообщения вероятность искажения одного знака равна р=0,01. В предположении независимости искажения знаков составить ряд распределения случайной величины Х – числа искажённых знаков при передаче сообщения состоящего из 5 знаков. Вычислить М(Х),

D(X), σ(Х). Построить многоугольник распределения дискретной случайной величины Х.

2. В ходе аудиторской проверки строительной компании аудитор случайным образом отбирает 5 счетов. Известно, что 3 % счетов содержат ошибки. Составить закон распределения случайной величины Х – числа правильных счетов. Вычислить М(Х), D(X), σ(Х). Построить многоугольник распределения дискретной случайной величины Х.

21

1.4. Числовые характеристики дискретных случайных величин

Наиболее полно описывает случайную величину, закон её распределения, который задаёт все возможные её значения и соответствующие вероятности. Однако зачастую нет необходимости характеризовать случайную величину так досконально. Бывает достаточно указать несколько параметров случайной величины.

Такие параметры, выражающие наиболее важные особенности случайной величины, называются числовыми характеристиками случайной величины.

Математическим ожиданием дискретной случайной величины называют сумму произведений всех её возможных значений на их вероятности.

Дисперсией дискретной случайной величины называют математическое ожидание квадрата отклонения случайной величины от её математического ожидания:

Средним квадратическим отклонением случайной величины X

называют квадратный корень из дисперсии

Понятие, характеристика и основные свойства математического ожидания и дисперсии независимых случайных величин приведены в табл. 3.

22