
- •П.Я. Бушин
- •Эконометрика
- •П.Я. Бушин
- •Эконометрика
- •Глава 2. Множественная корреляция и регрессия
- •Таблица дисперсионного анализа регрессии
- •Таблица 3.1
- •Поквартальные данные продажи учебников
- •Рис. 57. График исходных данных и тренда
- •Рис. 58. График сезонной компоненты
- •Таблица 3.2
- •Расчет прогноза с учетом сезонной компоненты
- •Рис.62. График прогноза по модели Винтера
- •Пример. Моделирование сезонной компоненты на основе фиктивных переменных
- •Как отмечалось выше (п. 2.3.4), сезонную компоненту можно моделировать и на основе фиктивных переменных. Выберем в качестве примера аддитивную модель сезонной декомпозиции и проиллюстрируем ее сходство с моделью с фиктивными переменными.
- •ОГЛАВЛЕНИЕ
- •Глава 2. Множественная корреляция и регрессия………………………………………..23
72
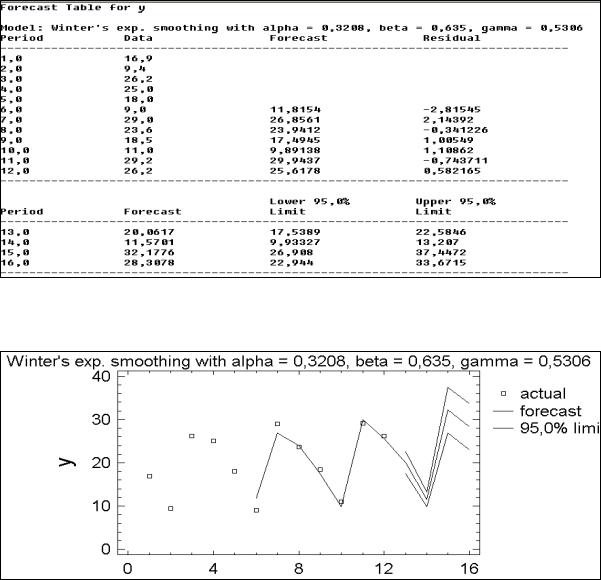
Рис. 61. Отчет о прогнозе по модели Винтера На рис. 62 приведен график прогноза, иллюстрирующий результаты расчетов,
приведенных на рис. 61.
Рис.62. График прогноза по модели Винтера
Пример. Моделирование сезонной компоненты на основе фиктивных переменных
Как отмечалось выше (п. 2.3.4), сезонную компоненту можно моделировать и на основе фиктивных переменных. Выберем в качестве примера аддитивную модель сезонной декомпозиции и проиллюстрируем ее сходство с моделью с фиктивными переменными.
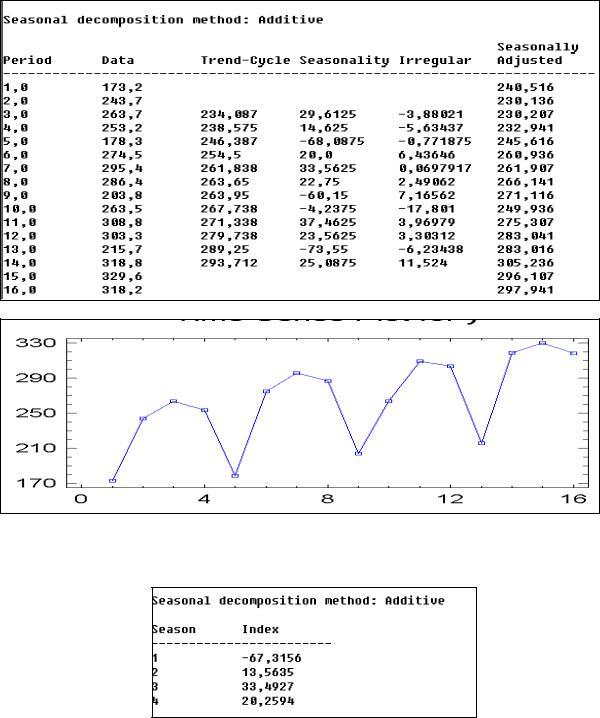
Пусть имеются данные о продажах продукции фирмы (см. информацию в столбце Data на рис. 63). Анализ горизонтального графика ряда (рис. 64) показал наличие тренда с сезонной компонентой. Применим метод сезонной декомпозиции (аддитивную модель), результаты которого показаны на рис. 63.
73
Рис. 63. Отчет о расчетах по методу сезонной декомпозиции по аддитивной модели
Рис. 64. Горизонтальный график ряда Ниже приведены результаты усреднения сезонно-случайной компоненты в виде
показателей, указывающих, на сколько усл. ден. единиц продажи выше или ниже средних по тренду.
Рис. 65. «Индекс» сезонности Далее приведен график этих показателей (рис. 66). Слово «индекс» взят в кавычки
потому, что здесь этот показатель выражен в абсолютных единицах изучаемого процесса (усл. ден. ед.), а не в долях или процентах, как это обычно присуще индексам в статистике.

74
Рис. 66. График «индекса» сезонности По приведенным расчетным показателям заключаем, что продажи в первом
квартале в среднем на 67,3 усл. ден. ед. меньше, чем по тренду, а в остальных кварталах
– выше на соответствующую величину.
Приведенный ниже (рис. 67) график данных, исправленных на сезонность показывает наличие тренда, который можно принять за линейный. Рассчитаем по этим данным линейный тренд.
Рис. 67. График данных, исправленных на сезонность
Результаты расчета линейного тренда приведены ниже (рис. 68).
Рис. 68. Уравнение линейного тренда (R2 = 87,5%, d = 1,82) Итак, уравнение тренда имеет вид
yˆ = 223.16 + 4.85t.
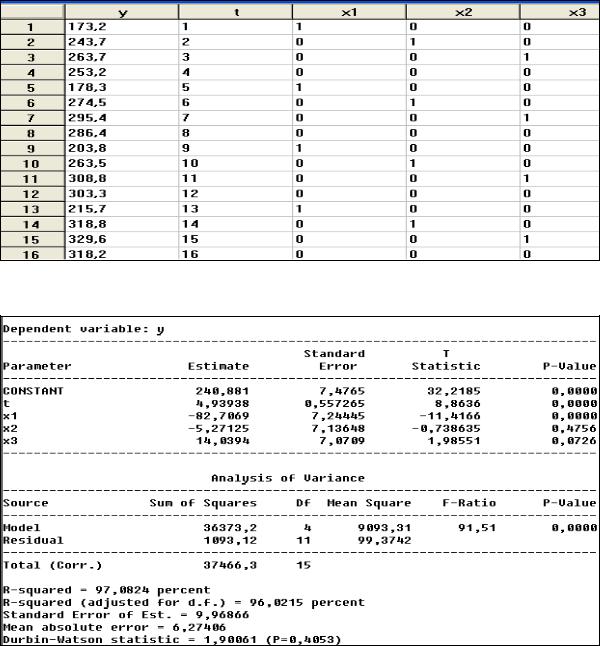
Проведем теперь моделирование сезонной компоненты с помощью фиктивных переменных. Как уже отмечалось, число таких переменных должно быть на единицу меньше, чем число уровней моделируемого явления. Т. к. у нас квартальные данные, то таких переменных будет три: х1, х2 и х3. Каждая из них равна единице для соответствующего квартала и равна нулю – для остальных, как это отражено на рис. 69.
75
Рис. 69. Исходные данные для модели с фиктивными переменными Результаты множественной регрессии с фиктивными переменными приведены на
рис. 70.
Рис. 70. Отчет о множественной регрессии при моделировании сезонной компоненты с помощью фиктивных переменных
Итак, уравнение регрессии имеет вид (с округлением)
yˆ = 240.9 + 4,94t – 82,71x1 – 5,27x2 + 14,04x3.
Таким образом, по сравнению с четвертым кварталом продажи в первом квартале ниже на 82,7 1 ед., во втором – ниже на 5,27 ед., а в третьем – выше на 14,04 ед. Средний постоянный уровень продаж равен 240.9 ед., а среднее ежеквартальное увеличение продаж равно 4,94 ед. (коэффициент при t).
Аналогичные результаты можно получить, сравнивая сезонные «индексы» для аддитивной модели. Так, разница между такими индексами для соответствующих кварталов следующая: S4 – S1 = 20,26 – (–67,32) = 87,58; S4 – S2 = 20,26 – 13,56 = 6,7;
S4 – S3 = 20,26 – 33,49 = –13,23.
76
Задания для самостоятельной работы Задание 1
К следующим временным рядам подобрать лучшую линию тренда в виде
аналитической кривой: |
|
|
|
|
а) 21,6 22,9 |
25,5 21,9 23,9 |
27,5 |
31,5 |
29,7 28,6 31,4 32,1 31,2; |
б) 146 106 |
123 89 97 |
74 |
80 |
53 56 35. |
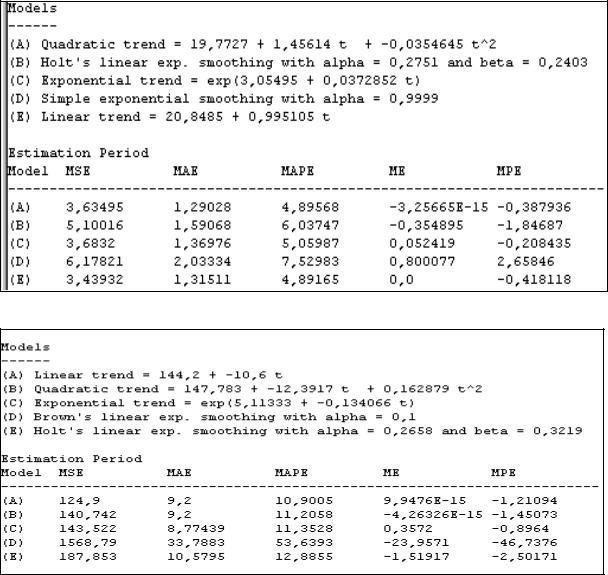
Изобразить в системе координат исходные данные и выбранную линию тренда. Ниже (рис. 71 и рис. 72) приведены отчеты о решении задач с помощью
статистического ППП. Вам необходимо его проанализировать и сделать соответствующие выводы по аналогии с тренировочным примером.
Рис. 71. Информация для решения задачи а)
Рис. 72. Информация для решения задачи б)
Прогноз сделать по линейному и квадратичному тренду.
Задание 2
Имеется следующая информация о потреблении электроэнергии жителями города за 4 года по кварталам (рис.73 в столбце Data).
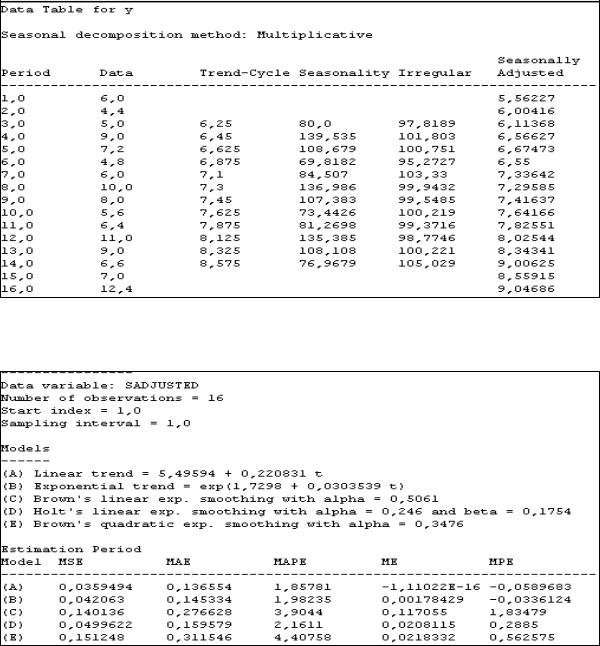
Используя результаты расчетов (рис. 73), построить график исходных данных и линию тренда по центрированным скользящим средним (столбец Trend-Cycle рис.73). Вычислить индексы сезонности, усреднив показатели сезонности (столбец Seasonality)
77
по соответствующим кварталам (например, для 3-го квартала необходимо сосчитать среднюю арифметическую из чисел с номерами 3, 7, и 11 в столбце Seasonality и т. д.).
Рис. 73. Информация для анализа задачи из задания 2 Построить график индексов сезонности.
Спрогнозировать потребление электроэнергии по линии тренда (выбрать лучшую линию тренда по данным на рис. 58)
Рис. 74. Окно отчета о подборе линии тренда Скорректировать прогноз по тренду с помощью индексов сезонности.
Задание 3
Для следующего ряда данных об объемах продаж некоторой фирмы по кварталам спрогнозировать объемы продаж на очередной 6-й год, выбрав наилучший тип модели:
350, 200, 150, 400, 550, 350, 250, 550, 550, 400, 350, 600, 750, 500, 400, 650, 850, 600, 450, 700.
Задание 4
Спрогнозировать на очередные 5 периодов процесс, характеризующийся следующими данными за 40 прошедших периодов, подобрав наилучший вид модели:
10,4 10,34 10,55 10,46 10,82 10,91 10,87 10,67 11,11 10,00 11,20 11,27 11,44 11,52
12,10 11,83 12,62 12,41 12,43 12,73 13,01 12,74 12,73 12,76 12,92 12,64 12,79 13,06 12,69
13,01 12,90 13,12 12,47 12,94 13,1 12,91 13,39 13,13 13,34 13,14.

78
Глава 4. Система одновременных эконометрических уравнений
4.1. Общие понятия о системах одновременных уравнений
Как ранее обсуждалось, остатки уравнений регрессии не должны зависеть от значений объясняющих (независимых) переменных. Однако возможны ситуации, когда на изменения и тех и других влияют одни и те же факторы. Это возможно, когда одни и те же внешние факторы одновременно формируют поведение зависимой и независимых переменных. В этом случае рассматриваемая модель не является полной и появляется необходимость ввести в нее уравнение, в котором объясняемыми переменными выступали бы зависимые переменные. Таким образом, появляется необходимость рассмотрения системы одновременных уравнений.
Классическим примером системы одновременных уравнений является модель формирования спроса и предложения товара в зависимости от его цены.
Пусть Qd – спрос на товар, Qs – предложение товара, Р – цена товара, У – доход. Составим следующую систему уравнений “спрос – предложение”:
Qd = |
|
0 |
+ |
|
1 |
Р + |
2 |
У + |
1 |
(предложение), |
(4.1) |
|
|
|
|
|
|
|
|
||||
Qs = |
0 |
+ |
1 |
Р + |
2 |
|
|
(спрос), |
(4.2) |
||
|
|
|
|
|
|
|
|
|
|||
Qs = Qd = Q |
|
|
|
|
|
|
(равновесие). |
(4.3) |
|||
Итак, имеем: предложение на товар формируется под влиянием цены и дохода, спрос на товар зависит от цены, а последнее равенство означает равновесие предложения и спроса. В этой системе уравнений Р – цена равновесия, которая формируется одновременно со спросом и предложением, следовательно, здесь Р и Q – зависимые переменные, а У – независимая.
Вдальнейшем, если значения переменных формируются в результате расчетов по модели, то такие переменные будут называться эндогенными (внутренними) переменными, в противном случае (если значения переменных определяются или задаются вне модели) – экзогенными (внешними).
Внашем случае У – экзогенная переменная, Р и Q – эндогенные.
Главное отличие между эндогенными и экзогенными переменными заключается в том, что остатки не зависят от экзогенных переменных и, как правило, зависят от эндогенных переменных. В нашем случае естественно предположить, что на спрос и цену равновесия влияют одни и те же случайные факторы.
Система одновременных уравнений кроме уравнений регрессий обычно содержит тождества, устанавливающие соотношения между эндогенными переменными. Тождества позволяют исключать некоторые эндогенные переменные и уменьшать размерность модели. Само тождество оценке не подлежит.
Так, в нашем случае, равенство Qs = Qd = Q приводит к системе уравнений:
Q = |
0 + |
1 Р + |
2 У + 1 , |
(4.4) |
Q = |
0 + |
1 Р + |
2 . |
(4.5) |
В этой системе уравнений зависимая (эндогенная) переменная Р находится в правой части уравнений. В общем случае для двух эндогенных и двух экзогенных переменных система одновременных уравнений может быть записана в виде
y1 = |
0+ |
12y2 + |
11x1 + |
12x2 + 1 , |
|
y2 = |
0+ |
21y1 + |
21x1 + |
22x2 + 2 . |
(*) |
Здесь одни и те же переменные (у1 и у2) одновременно рассматриваются как зависимые в одних уравнениях и как независимые в других. В эконометрике такая

79
система уравнений называется структурной формой модели, а ее коэффициенты – структурными коэффициентами модели. В такой системе уравнений каждое уравнение не может рассматриваться самостоятельно, и для оценки его параметров традиционный МНК неприменим. Для этого применяются специальные приемы оценивания.
Если в структурной форме модели эндогенные переменные выразить через экзогенные, то полученная система уравнений будет называться приведенной формой модели, а ее коэффициенты – коэффициентами приведенной формы модели.
В нашем случае это будет выглядеть следующим образом:
y1 = |
0+ |
11x1 + |
12x2 + 1, |
|
y2 = |
0 + |
21 x1 + |
22 x2 + 2. |
(**) |
Коэффициентами приведенной формы модели являются функциями коэффициентов структурной формы модели и могут быть определены при решении системы структурных уравнений относительно экзогенных переменных.
4.2. Косвенный метод наименьших квадратов
Косвенный метод наименьших квадратов предназначен для оценки структурных параметров системы одновременных уравнений. Идея этого метода заключается в следующем. Известно, что оценивать каждое уравнение структурной модели по отдельности не рекомендуется (в этом случае оценки могут быть смещенными и неэффективными в силу коррелированности эндогенных переменных с остатками). Поэтому сначала обычным МНК оцениваются параметры приведенной формы модели, а затем эти оценки используются для определения оценок параметров структурной формы.
Такой метод оценки называется косвенным МНК. Проиллюстрируем этот метод на примере.
Рассмотрим модель формирования спроса и предложения товара в зависимости от его цены, описанную в п. 4.1. Пусть имеется информация для этой модели по 15 периодам времени (рис. 75):
Рис. 75. Исходная информация для рассматриваемого примера Оценим параметры системы одновременных уравнений (4.4) – (4.5) косвенным
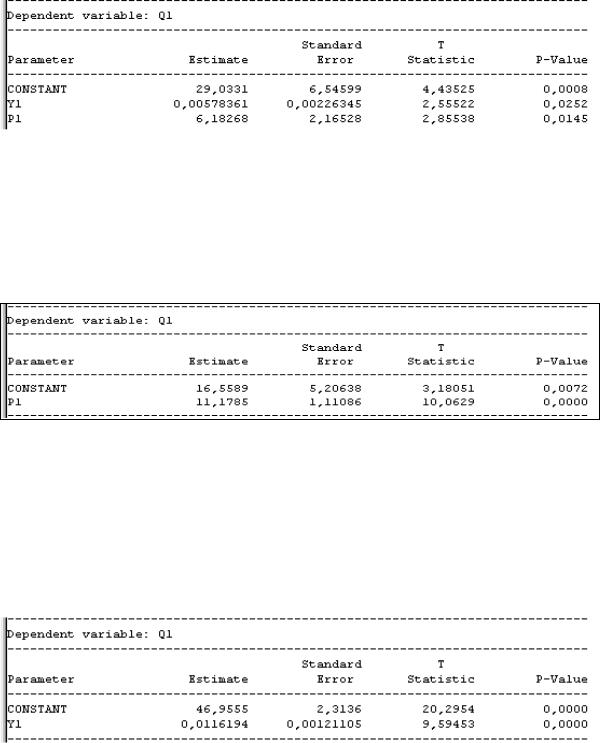
МНК. Для этого оценим сначала каждое уравнение этой системы обычным МНК. Получим для уравнения (4.4) (см. рис. 76).
80
|
|
|
Рис. 76. |
Оценка уравнения (4.4) обычным МНК (R2 = 93%, d = 2,03) |
|
Имеем |
ˆ |
(4.6) |
Q = 29,033 + 0,0058*Y + 6.183*P. |
||
Коэффициент множественной детерминации, равный 93 %, показывает, что уравнение регрессии довольно точно воспроизводит зависимость спроса от дохода и цены. Коэффициент Дарбина – Уотсона, равный 2,03, показывает, что автокорреляция в остатках отсутствует. Но поскольку в правой части уравнения находится зависимая переменная Р, то предполагается, что остатки коррелируют с факторными переменными, нарушая тем самым предпосылки МНК и регрессионного анализа
Для уравнения (4.5) обычный МНК дает (рис. 77):
Рис. 77. Оценка уравнения (5,5) обычным МНК (R2 = 88,4%, d =1,97).
Имеем |
ˆ |
(4.7) |
Q = 16,559 + 11,1785*Р. |
И здесь уравнение регрессии значимо, на 84,4 % описывает изменение предложения от изменения цены, а коэффициент Дарбина – Уотсона, равный 1,97, показывает, что автокорреляция в остатках отсутствует. Однако считается, что остатки в этих уравнениях могут коррелировать с регрессорами.
Применим к этой системе косвенный МНК. Для этого запишем уравнения линейной регрессии для P и Q в зависимости от объясняющей переменной Y – доход.
ˆ |
+ b1*Y |
и |
ˆ |
= a2 + b2*Y. Оценки этих уравнений дают следующие |
P = a1 |
Q |
результаты (рис. 78 и 79).
|
|
|
|
|
|
|
ˆ |
+ b2*Y (R |
2 |
= 87,6%, d = 2,15) |
|
Рис. 78. Оценка уравнения Q = a2 |
|
||||
Имеем |
ˆ |
|
|
|
(4.8) |
Q = 46,95 + 0,00116*Y. |
|||||
Коэффициент детерминации = 87,6%, статистика Дарбина – Уотсона = 2,15. Это значит, что уравнение регрессии значимо, точное и без автокорреляции в остатках.

81
|
|
|
|
|
Рис. 79. Оценка уравнения |
ˆ |
+ b1*Y (R |
2 |
= 81,5%, d = 2,34) |
P = a1 |
|
ˆ
Имеем P = 2,899 + 0,00094*Y. (4.9)
И это уравнение достаточно точное.
Воспользуемся последними двумя уравнениями (4.8) и (4.9) для получения оценок параметров системы уравнений (4.4) – (4.5).
Для оценки параметров уравнения (4.5) выразим Q через P, подставив Y из (4.9) в
(4.8). Получим |
ˆ |
(4.10) |
Q = 11,27 + 12,31*P. |
Сравните с (4,7). Как видим, различие есть.
Для оценки параметров уравнения (4.4) сложим (4.8) и (4.9). Получим
ˆ |
(4.11) |
Q = 49,7 – P + 0.013*Y. |
Как видим, отличие полученного уравнения от уравнения (4.6) значимое, т. е. оценки, полученные на основе обычного МНК и косвенного МНК, различаются.
Вто же время, как показывают расчеты, результаты, полученные по этим уравнениям при оценке по ним значений зависимых переменных, различаются незначимо.
Предполагается, что оценки, полученные косвенным МНК, состоятельные и несмещенные.
4.3. Проблемы идентифицируемости
Врассмотренном примере мы сумели на основе оценок параметров приведенной формы системы уравнений (4.8) и (4.9) однозначно найти оценки параметров структурной формы системы уравнений. Оказывается, что такая ситуация имеет место не всегда.
Бывают ситуации, когда на основе оценок параметров приведенной формы системы уравнений (**), получаемых обычным МНК, однозначно получить оценки параметров структурной формы системы уравнений (*) не удается. Более того, иногда их вообще нельзя рассчитать. Но именно структурная форма раскрывает механизм формирования значений экзогенных переменных и оценка ее параметров является целью рассмотрения системы одновременных эконометрических уравнений.
Рассмотрим эту проблему подробнее.
Структурный параметр называется идентифицируемым, если он может быть однозначно оценен с помощью косвенного МНК. В этом случае (грубо говоря) число параметров структурной модели должно быть равно числу параметров приведенной формы модели. В этом случае число уравнений для определения коэффициентов структурных уравнений равно количеству этих коэффициентов.
Уравнение идентифицируемо, если идентифицируемы все входящие в него структурные параметры. Модель идентифицируема, если все ее уравнения идентифицируемы.
Структурный параметр называется неидентифицируемым, если его значение невозможно получить, даже зная точные значения параметров приведенной формы. Модель неидентифицируема, если хотя бы один её структурный параметр неидентифицируем. В этом случае число приведенных коэффициентов меньше числа структурных коэффициентов.
82
Параметр называется сверхидентифицированным, если косвенный МНК дает несколько равноправных оценок этого параметра. Модель сверхидентифицируема, если число приведенных коэффициентов больше числа структурных коэффициентов. В этом случае число уравнений для определения коэффициентов структурных уравнений больше количества этих коэффициентов.
Проблема идентифицируемости связана не только с числом приведенных и структурных коэффициентов. Может оказаться, что их число совпадает, но при выражении структурных коэффициентов через приведенные полученная система уравнений неразрешима. Достаточным условием идентифицируемости является невырожденность матрицы коэффициентов системы уравнений, связывающих структурные коэффициенты с приведенными. Более подробно об этом можно найти в литературе по эконометрике.
4.4. Двухшаговый метод наименьших квадратов (метод инструментальных переменных)
Если система сверхидентифицируема, то косвенный МНК неприменим, т. к. он не дает однозначных оценок для параметров структурной модели. В этом случае можно использовать различные методы оценивания параметров структурной модели, но наиболее часто используется двухшаговый МНК.
Основная идея этого метода состоит в использовании инструментальных переменных, на основе которых фактические значения эндогенных переменных в правой части уравнения заменяются на расчетные, полученные обычным МНК, с дальнейшим применением обычного МНК к полученным данным. Тем самым обеспечивается независимость регрессоров (факторных переменных) от остатков регрессии. Процедура замены фактических значений эндогенных переменных в правой части уравнений на их расчетные значения называется очищением факторной переменной от ее зависимости от остатков. При этом удаляется та часть переменной, которая коррелирует с ошибками регрессии. Расчетные значения факторных переменных и образуют инструментальные переменные.
Рассмотрим пример, иллюстрирующий описанную процедуру. Пусть
рассматривается модель вида |
|
Y = a1 + b1(C + D) + e1, |
|
C = a2 + b2 *Y + b3*Y-1 + e2, |
(4.12) |
где Y – валовой национальный доход текущего года;
Y-1 – валовой национальный доход предшествующего года; С – личное потребление;
D – конечный спрос (помимо личного потребления); e1 и e2 – случайные составляющие.
В эконометрических исследованиях переменные, сдвинутые по времени на некоторый промежуток времени. называются лаговыми и в системах одновременных уравнений рассматриваются, как правило, в качестве экзогенных переменных. В нашем случае к таким переменным относится Y-1. Кроме того, поскольку на переменные С и D наложено условие, что они должны входить в модель с одинаковыми коэффициентами, то переменная С в первом уравнении рассматривается как экзогенная (она участвует в уравнении не самостоятельно, а вместе с переменной D). Таким образом, в данной модели две экзогенные переменные (D и Y-1) и две эндогенные (Y и С). В нашем случае оценке подлежат пять параметров структурной формы модели, т. е. нужно рассчитать коэффициенты а1, а2, b1, b2 и b3 по шести коэффициентам приведенной формы модели, т. е. имеем случай сверхидентифицируемой модели.
Пусть имеется следующая условная информация за 14 лет о приростах этих показателей (рис.80).

83
Рис. 80. Исходная информация для двухшагового МНК.
Рассчитаем по этой информации уравнения в приведенной форме, используя МНК. Имеем для 1-го приведенного уравнения (рис. 81).
Рис. 81. Оценка 1-го приведенного уравнения (R2 = 93 и d = 2,8) Для второго приведенного уравнения (рис. 82).
Рис. 82. Оценка 2-го приведенного уравнения (R2 = 90,2, d = 1,16) Приведенная форма модели имеет вид
ˆ = 7,9 + 0,49*D + 0,42*Y-1,
Y
ˆ = 2,02 + 0,26*D + 0,22*Y-1.
С
Для оценки пяти параметров структурной формы модели найдено шесть коэффициентов приведенной формы модели. Т.е. наша система уравнений сверхидентифицируема, поскольку сверхидентифицируемым является первое уравнение, т. к. на его параметры наложено условие, что два из них (перед С и D) должны быть равны.
Для оценки параметров сверхидентифицированной модели используем двухшаговый МНК, для чего по второму уравнению из системы приведенной формы
определим расчетные значения ˆ , а затем в первом уравнении структурной формы
С
(оно сверхидентифицируемо) заменим фактические значения С на расчетные значения
ˆ |
ˆ |
С |
и рассчитаем новую переменную Z = С + D и затем на основе обычного МНК |
оценим параметры преобразованного первого уравнения структурной формы. В данном
случае ˆ и Z будут являться инструментальными переменными.
С
84
ˆ
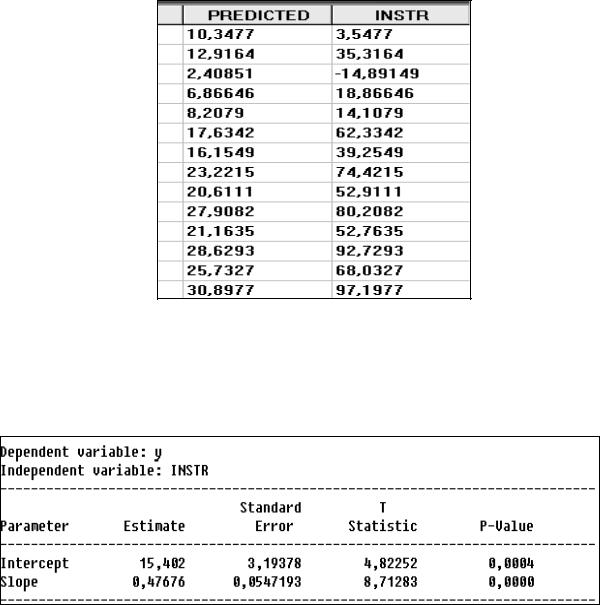
Расчет инструментальных переменных С и Z приведен на рис. 83.
Рис. 83. Результаты расчета инструментальной переменной
Первый столбик цифр (PREDICTED) – это предсказанные (расчетные) значения
ˆ |
ˆ |
переменной С, т. е. С , а второй (INSTR) – сумма значений переменных |
С и D. Здесь |
использована возможность сохранения результатов вычислений в файле исходных данных, а также процедура преобразования переменных в ППП Statgraphics.
Коэффициенты уравнения ˆ = a1 + b1(C + D), рассчитанные по обычному МНК,
Y
приведены ниже (рис. 84).
Рис. 84. Оценка 1-го уравнения обычным МНК (R2 = 92,9, d = 2,5)
Имеем ˆ = 15,4 + 0,48* (C + D).
Y
Итак, первое уравнение структурной формы оценено.
Для оценки второго уравнения воспользуемся приведенными уравнениями и выразим из них зависимость личного потребления от валового национального дохода текущего и предыдущего периодов.
Из первого уравнения получим D = –16,12 + 2,04*Y – 0.86*Y-1. Подставив это
выражение во второе уравнение, получим ˆ = –4,17 + 32,88* Y –13,64 * Y -1.
С
Второе уравнение структурной формы также оценено. Итак, имеем
ˆ = 15,4 + 0,48* (C + D)
Y
ˆ = –2,17 + 0,53*Y –1,53*Y -1.
С
Приведем для сравнения оценки структурной формы модели с использованием обычного МНК.
Для первого уравнения получим (рис. 85)

85
Рис. 85. Оценка 1-го структурного уравнения (R2= 93,4, d =2,32)
Первое уравнение |
ˆ |
= 15,36 + 0,48*(C + D). |
Y |
Для второго уравнения получим (рис.86)
Рис. 86. Оценка 2-го структурного уравнения (R2= 89,7, d =1,43)
Второе уравнение ˆ = -1,84 + 0,49* Y + 0.025* Y -1.
С
Сравнивая уравнения, полученные на основе обычного МНК, с уравнениями, полученными по двухшаговому МНК, видим, что различий для первого уравнения почти нет (см. рис. 84 и рис. 85), а для второго – различия значимы (даже по знаку при переменной Y-1), Но главное здесь в том, что оценки по двухшаговому МНК проведены в условиях выполнимости предпосылок МНК, а потому считается, что эти оценки не смещенные, эффективные и состоятельные.
4.5. Трехшаговый метод наименьших квадратов
Трехшаговый метод наименьших квадратов обычно используется в случае, если в структурной форме модели ошибки коррелируют друг с другом. В этом случае к структурной форме сначала применяется обобщенный МНК для ликвидации отмеченной коррелированности, а затем используется двухшаговый МНК.
Ясно, что если ошибки не коррелируют, то трехшаговый МНК сводится к двухшаговому МНК.
Отметим в заключение темы, что системы уравнений регрессии могут быть различных типов. Например, система независимых уравнений; такая система оценивается обычным МНК (каждое уравнение по отдельности). Или система рекурсивных уравнений, в которой зависимые переменные последовательно включаются в каждое последующее уравнение в качестве факторных наряду с собственно факторными переменными. В этом случае каждое уравнение может последовательно рассматриваться как самостоятельное и его параметры могут оцениваться обычным МНК.
86
Библиографический список
1. Айвазян С. А., Мхитарян В. С. Прикладная статистика и основы эконометрики : учебник для вузов. – М. : ЮНИТИ, 1998.
2. Афанасьев В. Н., Юзбашев М. М. Анализ временных рядов и прогнозирование : учебник. – М. : Финансы и статистика, 2001.
3. Боровиков В. SATISTICA: Искусство анализа данных на компьютере. Для профессионалов. – СПб. : Питер, 2001.
4.Бушин П. Я. Статистические методы принятия решений : уч. пособ. – Хабаровск,
2002.
5.Вуколов Э. А. Основы статистического анализа. Практикум по статистическим методам и исследованию операций с использованием пакетов STATISTICA и EXEL : уч. пособ. – М. : ФОРУМ; ИНФРА-М, 2004.
6.Дрейпер Н. , Смит Г. Прикладной регрессионный анализ. – 2-е изд., перераб. и доп. Кн.1 / пер. с англ. – М. : Финансы и статистика, 1986.
7.Дубров А. М. , Мхитарян В. С. , Трошин Л. И. Многомерные статистические
методы. Для экономистов и менеджеров: учебник. М. : – Финансы и статистика, 1998. 8. Дюк В. Обработка данных на ПК в примерах. – СПб. : Питер, 1997.
9.Ежеманская С. Н. Эконометрика ( Серия «Учебники, учебные пособия»). – Ростов н/Д : Феникс, 2003.
10.Крамер Г. Математические методы статистики. – 2-е изд. / пер. с англ. – М. :
Мир, 1975.
11.Кремер Н. Ш. , Путко Б. А. Эконометрика : учебник для вузов / под ред. проф. Н. Ш. Кремера. – М. : ЮНИТИ-ДАНА, 2002.
12.Лукашин Ю. П. Адаптивные методы краткосрочного прогнозирования. – М. : Статистика, 1979.
13. Льюис К. Д. Методы прогнозирования экономических показателей / пер. с англ.
– М. : Финансы и статистика, 1986.
14. Магнус Я. Р. , Катышев П. К. , Пересецкий А. А. Эконометрика. Начальный курс: учебник. – 3-е изд., перераб. и доп. – М. : Дело, 2000.
15. Попов Л. А. Анализ и моделирование трудовых показателей : учебник. – 2-е изд., доп. и перераб. – М. : Финансы и статистика, 1999.
16. Практикум по эконометрике : учеб. пособ. / под ред. И. И. Елисеевой. – М. : Финансы и статистика, 2001.
17.Салманов О. Н. Математическая экономика с применением Mathcad и Exel. – СПб. : БХВ-Петербург, 2003.
18.Сигел Эндрю. Практическая бизнес-статистика : пер. с англ. – М. : Издательский дом «Вильямс», 2002.
19.Сошникова Л. А. , Тамашевич В. Н. , Уебе Г. , Шефер М. Многомерный статистический анализ в экономике : учеб. пособ. для вузов / под ред. проф. В. Н. Тамашевича. – М. : ЮНИТИ-ДАНА, 1999.
20.Тихомиров Н. П. , Дорохина Е. Ю. Эконометрика : учебник. – М. : Экзамен,
2003.
21.Френкель А. А. Прогнозирование производительности труда: методы и модели. – М. : Экономика, 1989.
22.Ханк Д. Э., Уичерн Д. У. Райтс А. Дж. Бизнес-прогнозирование. – 7-е изд./пер.
сангл. – М. : Вильямс, 2003.
23. Четыркин Е. М. Статистические методы прогнозирования. – 2-е изд., перераб. и доп. – М. : Статистика, 1977.
