
- •Моделирование производственных процессов и финансовых операций
- •Хабаровск 2008
- •ВВЕДЕНИЕ
- •Исследуем отдачу от расширения масштабов производства и взаимосвязь между эластичностью производства и коэффициентами эластичности выпуска по производственным факторам.
- •Для случая двух переменных K и L однородность производственной функции F(K, L) определяется соотношением (1.4):
- •Рис.1.1. Изокванта и предельная норма замещения труда капиталом hLK
- •Рис.1.2. Изокванты и изоклинали производственной функции
- •Рис.1.4. Изокванты линейной производственной функции
- •Параметры в традиционных линейной производственной функции (1.20)
- •Следовательно, производственные функции с переменными параметрами являются обобщением производственных функций с постоянными параметрами.
- •Отрицательность параметров статических производственных функций (1.20) и (1.21) указывает на неадекватность описания этими функциями экономики США.
- •Таким образом, несмотря на очень высокие значения коэффициентов детерминации, статические производственные функции (1.20) и (1.21) не пригодны для моделирования экономики США.
- •Воспользовавшись оценками макроэкономической степенной производственной функции экономики США периода 1950 – 1960 гг.
- •Для построения изокванты степенной производственной функции постоянного выпуска Y0=535,2 млрд долл. определим по формуле (1.64) расчётные значения объёма основного капитала K в зависимости от количества отработанных часов L (табл. 1.8).
- •Таблица 1.8
- •Расчёт величин K(L) и h
- •Из (2.3) следует
- •Таблица 2.1
- •Финансовые функции ППП Excel
- •План погашения кредита периодическими взносами
- •План погашения кредита равными частями основного долга
- •План погашения кредита равномерными взносами
- •библиографический СПИСОК
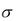
Из формулы (1.63) следует:
-предельная норма замещения в линейной производственной функции с переменными параметрами является переменной, так как переменными являются параметры предельных эффективностей факторов at и bt;
-переменность предельной нормы замещения производственных факторов в степенной производственной функции с переменными параметрами обусловлена не только соотношением производственных факторов, но и соотношением переменных коэффициентов эластичности выпуска производственных факторов.
Нетрудно заметить, что степенная производственная функция с переменными параметрами (1.58) удовлетворяют всем четырём предположениям (1.1) – (1.4) о свойствах производственных функций. Следует также отметить, что в производственных функциях с переменными параметрами преодолевается ограниченность постоянства эластичности замещения производственных факторов в функциях CES.
Переменность эластичности замещения производственных факторов (t) производственной функции с переменными параметрами позволяет исследовать возможность замещения производственных факторов не в целом для всего анализируемого периода времени, как в случае производственных функций CES с постоянной эластичностью замещения, а для каждого конкретного года в зависимости от соотношения темпов прироста факторов и параметров производственной функции.
Таким образом, благодаря гипотезе о переменности параметров в производственных функциях преодолевается методологическая проблема ограниченности традиционных производственных функций с постоянными параметрами, заключающаяся в постоянстве эластичности замещения производственных факторов.
Следовательно, производственные функции с переменными параметрами являются обобщением производственных функций с постоянными параметрами.
Прогнозирование с помощью статических производственных функций осуществляется традиционными методами. Для прогнозирования производственных функций с переменными параметрами автором разработаны новые методы преобразования этих производственных функций.
42

1.2. ЭКСПЕРИМЕНТАЛЬНОЕ ОЦЕНИВАНИЕ И ВЫБОР СТАТИЧЕСКИХ ПРОИЗВОДСТВЕННЫХ ФУНКЦИЙ
Статистические данные экономики США приведены в табл. 1.1.
В качестве конечного результата производства выбран валовой национальный продукт Yt, а в качестве факторов производства – объём загруженного основного капитала Kt и количество отработанных часов в производстве Lt.
По данным валового национального продукта Yt, объёма загруженного основного капитала Kt и количества отработанных часов в производстве Lt экономики США 1950 – 1960 гг. (табл.1.1) необходимо:
1.Оценить методом наименьших квадратов параметры линейной и степенной производственных функций.
2.Выбрать из оценённых производственных функций ту функцию, которая точнее описывает экономический процесс.
3.Сравнить характеристики линейной и степенной производственных функций.
4.Исследовать свойства и характеристики статической степенной производственной функции.
43
Таблица 1.1 Динамика основных показателей экономики США 1950 – 1960 гг.
Год |
Y |
K |
L |
|
Валовой |
Объём загруженного |
Количество отработанных часов, |
|
национальный |
основного капитала (в |
млрд ч |
|
продукт (в ценах |
ценах 1972 года), млрд |
|
|
1972 года), млрд |
долл. |
|
|
долл. |
|
|
1950 |
534,8 |
310,42 |
125,12 |
1951 |
579,4 |
337,79 |
133,01 |
1952 |
600,8 |
349,20 |
134,91 |
1953 |
623,6 |
380,53 |
136,07 |
1954 |
616,1 |
354,20 |
131,12 |
1955 |
657,5 |
400,66 |
134,16 |
1956 |
671,6 |
415,15 |
136,04 |
1957 |
683,8 |
418,83 |
134,77 |
1958 |
680,9 |
384,87 |
130,44 |
1959 |
721,7 |
431,04 |
133,87 |
1960 |
737,2 |
435,65 |
134,99 |
1.2.1. Статистическая оценка и выбор производственных функций
По экспериментальным данным валового национального продукта Yt, объёма загруженного основного капитала Kt и количества отработанных часов в производстве Lt экономики США (табл.1.1) за период 1950 –1960 гг. после оценивания методом наименьших квадратов параметров линейной и степенной производственных функций выберем из них ту функцию, которая точнее описывает экономический процесс.
Для оценивания методом наименьших квадратов параметров линейной и степенной производственных функций воспользуемся пакетом прикладных программ (ППП) EXCEL. Для выбора линейной регрессии необходимо выполнить последовательный выбор из меню: Сервис/Анализ данных/Регрессия. В результате имеем диалоговое окно (рис. 1.5).
Заполнив все требуемые ячейки диалогового окна для экономики США за период 1950 – 1960 гг., получаем табл. 1.2 Выводы итогов оценивания параметров статической линейной производственной функции Y=A*+a·K+b·L произвольной степени однородности.
44
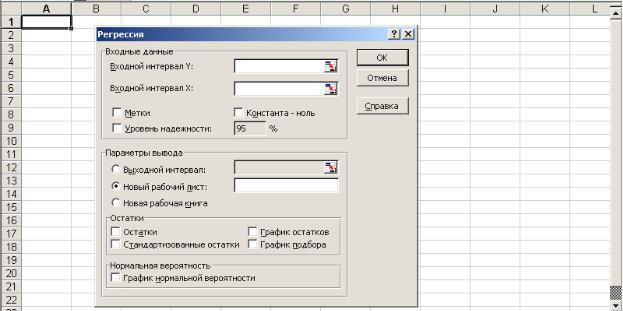
Рис. 1.5. Диалоговое окно Сервис/Анализ данных/Регрессия
Таблица 1.2 Вывод итогов оценивания параметров статической линейной
производственной функции Y=A*+a·K+b·L
ВЫВОД ИТОГОВ |
|
|
|
|
|
|
|
|
|
|
|
|
|
Регрессионная статистика |
|
|
|
|
|
|
Множественный R |
|
0,970 |
|
|
|
|
R-квадрат |
|
0,942 |
|
|
|
|
Нормированный R-квадрат |
|
0,927 |
|
|
|
|
Стандартная ошибка |
|
16,597 |
|
|
|
|
Наблюдения |
|
11 |
|
|
|
|
|
|
|
|
|
|
|
Дисперсионный анализ |
|
|
|
|
|
|
|
df |
|
SS |
MS |
F |
Значимость F |
Регрессия |
|
2 |
35518,2 |
17759,1 |
64,4678 |
1,2E-05 |
Остаток |
|
8 |
2203,8 |
275,473 |
|
|
Итого |
|
10 |
37722,0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Стандартная |
|
|
|
|
Коэффициенты |
ошибка |
t-статистика |
P-Значение |
Нижние 95% |
|
Y-пересечение |
|
417,1 |
251,2 |
1,7 |
0,1 |
-162,2 |
Переменная X 1 |
|
1,6 |
0,2 |
9,3 |
1,4E-05 |
1,2 |
Переменная X 2 |
|
-2,8 |
2,2 |
-1,3 |
0,2 |
-7,8 |
Для оценивания степенной производственной функции необходимо
45
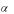
преобразовать исходные статистические данные валового национального продукта Yt, объёма загруженного основного капитала Kt и количества
отработанных часов в производстве Lt |
экономики США в логарифмы |
||
соответствующих показателей lnYt, lnKt, lnLt (табл. 1.3). |
|||
|
|
|
Таблица 1.3 |
Расчёт логарифмических показателей lnYt, lnKt, lnLt экономики США |
|||
|
|
|
|
Год |
lnYt |
lnKt |
lnLt |
1950 |
6,2819 |
5,7379 |
4,8293 |
1951 |
6,3620 |
5,8224 |
4,8904 |
1952 |
6,3983 |
5,8556 |
4,9046 |
1953 |
6,4355 |
5,9416 |
4,9132 |
1954 |
6,4234 |
5,8699 |
4,8761 |
1955 |
6,4884 |
5,9931 |
4,8990 |
1956 |
6,5097 |
6,0286 |
4,9129 |
1957 |
6,5277 |
6,0375 |
4,9036 |
1958 |
6,5234 |
5,9529 |
4,8709 |
1959 |
6,5816 |
6,0662 |
4,8969 |
1960 |
6,6029 |
6,0768 |
4,9052 |
Для оценивания методом наименьших квадратов параметров степенной производственной функции необходимо снова воспользоваться пакетом прикладных программ (ППП) EXCEL и осуществить последовательный выбор из меню: Сервис/Анализ данных/Регрессия. Следует обратить внимание, что в этом случае при заполнении диалогового окна вместо исходных данных валового национального продукта Yt, объёма загруженного основного капитала Kt и количества отработанных часов в производстве Lt экономики США необходимо использование логарифмов соответствующих показателей lnYt, lnKt, lnLt (табл. 1.3).
Для статической степенной производственной функции Y=A·K ·L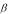 вывод итогов аналогичен виду вывода итогов линейной производственной функции (табл. 1.2).
вывод итогов аналогичен виду вывода итогов линейной производственной функции (табл. 1.2).
Из полученных итогов выпишем результаты оценивания параметров линейной и степенной производственных функций произвольной степени однородности и значения коэффициентов детерминации R2:
Ŷ =417,1+1,6*K - 2,8*L, R2 = 0,942;
46
