
5196
.pdfМинистерство образования и науки Российской Федерации Федеральное агентство по образованию
Государственное образовательное учреждение высшего профессионального образования
«Хабаровская государственная академия экономики и права»
МАТЕМАТИКА
Теория вероятностей и математическая статистика
Программа, методические указания к самостоятельному изучению дисциплины и контрольные задания
для студентов заочной формы обучения
Хабаровск 2007
ББК В 1
Х 12
Математика. Теория вероятностей и математическая статистика : программа, методические указания к самостоятельному изучению дисциплины и контрольные задания для студентов заочной формы обучения / сост. Е. Н. Кравченко, С. А. Наумова, И. В. Ясеновская. – Хабаровск : РИЦ ХГАЭП, 2007. – 64 с.
Рецензенты: В. М. Манаков, канд. физ.-мат. наук, доцент кафедры высшей математики ТОГУ
В. Я. Прудников канд. физ.-мат. наук, доцент кафедры высшей математики ТОГУ
Методические указания посвящены разделу "Теория вероятностей и математическая статистика" государственного общеобразовательного стандарта в области математики для специалистов с высшим образованием по экономическим специальностям. Дано краткое содержание каждой темы, приведены основные теоретические положения и используемые формулы, имеются образцы решения экономических задач с помощью современных прикладных математических методов обработки статистических данных.
Утверждено издательско-библиотечным советом академии в качестве методических указаний для студентов.
© Е. Н. Кравченко, С. А. Наумова, И. В. Ясеновская, 2007 ©Хабаровская государственная академия экономики и права, 2007
ОГЛАВЛЕНИЕ
Предисловие…………………………………………………..….......................4
Программа курса «Теория вероятностей и математическая статистика»…..5
Тема 1. Основные понятия теории вероятностей. Классическое определение вероятности……………………………………………………...7
Тема 2.Классические теоремы теории вероятностей………..……………9
Тема 3. Формула полной вероятности. Формула Байеса……………….11
Тема 4. Повторные независимые испытания……………….……………12
Тема 5. Случайные величины и их числовые характеристики…………15
Тема 6. Выборочный метод………………………………………………25
Тема 7. Статистические оценки параметров распределения…….……..29
Тема 8. Элементы теории корреляции………………….…......................32
Контрольные задания…………………………………………………………39
Библиографический список…………..………………………………………59
Приложения..……………………..…………...………………………………60
ПРЕДИСЛОВИЕ
Современный период развития науки характеризуется широким применением вероятностных (статистических) методов во всех областях знаний. Особенно большое значение теория вероятностей и математическая статистика имеют для современных экономических методов.
Студентам, изучающим курс теории вероятности и математической статистики, надо помнить, что данный курс имеет непосредственное применение к практике экономиста, а также используется при изучении дисциплины «Экономико-математические методы и модели».
Данная разработка содержит программу курса, список учебной литературы, основные теоретические вопросы дисциплины, решение типовых задач и задания для самостоятельного решения. Основные теоремы, выводы из них и математические формулы чаще всего даются без доказательства, чтобы основное внимание было сосредоточено на методике решения прикладных задач.
Методические указания соответствуют требованиям государственных общеобразовательных стандартов в области математики для специалистов с высшим образованием по экономическим специальностям и предназначены для самостоятельного изучения дисциплины студентами заочного отделения сокращённой формы обучения.
Составители желают студентам успехов в самостоятельном изучении курса теории вероятностей и математической статистики.
ПРОГРАММА КУРСА «ТЕОРИЯ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА»
Комбинаторика. Предмет теории вероятностей. Виды случайных событий. Классическое определение вероятности. Ограниченность классического определения. Относительная частота. Устойчивость относительных частот. Статистическое определение вероятности. Теорема сложения вероятностей для несовместных событий. Полная группа событий. Противоположные события. Зависимые и независимые события. Теорема умножения вероятностей. Вероятность появления хотя бы одного события.
Повторные испытания. Формула Бернулли. Наивероятнейшее число наступления событий. Локальная теорема Лапласа. Функция (х) и её свойства. Формула Пуассона. Интегральная теорема Лапласа. Функция Ф(х) и её свойства. Вероятность отклонения относительной частоты от постоянной вероятности в независимых испытаниях.
Случайные величины, их виды. Закон распределения вероятностей дискретной случайной величины. Определение функции распределения. Свойства функции распределения, её график. Определение непрерывной случайной величины. Плотность распределения вероятностей. Вероятность попадания непрерывной случайной величины в заданный интервал. Свойства функции плотности. Нахождение функции распределения по известной функции плотности.
Математическое ожидание дискретной случайной величины. Вероятностный смысл математического ожидания. Свойства математического ожидания. Дисперсия дискретной случайной величины. Формула для вычисления дисперсии. Свойства дисперсии. Среднее квадратическое отклонение. Числовые характеристики непрерывных случайных величин. Биномиальное распределение, его числовые характеристики. Распределение Пуассона, его числовые характеристики. Закон равномерного распределения вероятностей, его числовые характеристики. Нормальное распределение. Нормальная кривая. Влияние параметров нормального распределения на формулу нормальной кривой. Вероятность попадания в заданный интервал нормальной случайной величины. Правило «трёх сигм».
Неравенство Чебышева. Теорема Чебышева. Теорема Бернулли. Генеральная и выборочная совокупности. Виды выборки. Способы
отбора. Статистическое распределение выборки. Полигон и гистограмма. Эмпирическая функция распределения. Статистические оценки параметров распределения. Несмещенные, эффективные и состоятельные оценки. Оценка генеральной средней по выборочной средней. Устойчивость выборочных средних. Выборочная дисперсия. Оценка
генеральной дисперсии по исправленной выборочной. Точность оценки, доверительная вероятность (надежность). Доверительный интервал. Доверительный интервал для оценки математического ожидания нормального распределения при известном σ. Понятие о распределении Стьюдента. Доверительный интервал для оценки математического ожидания нормального распределения при неизвестном σ. Оценка истинного значения измеряемой величины.
Функциональная, статистическая и корреляционная зависимость. Две основные задачи теории корреляции. Отыскание параметров выборочного уравнения прямой линии регрессии. Свойства выборочного коэффициента корреляции. Групповая и общая средняя. Групповая, внутригрупповая, межгрупповая дисперсии. Криволинейная корреляция.
Статистические гипотезы. Нулевая и конкурирующая гипотезы. Простая и сложная гипотезы. Ошибки первого и второго рода, уровень значимости. Статистический критерий проверки нулевой гипотезы. Наблюдаемое значение критерия. Критическая область и область принятия гипотезы. Критические точки. Левосторонняя и правосторонняя критическая область. Отыскание критических областей. Мощность критерия. Критерий согласия. Примеры критериев согласия. Проверка гипотез о распределении Пуассона и о нормальном распределении совокупности с помощью критерия согласия Пирсона. Методики вычисления теоретических частот распределения Пуассона и нормального распределения.

ТЕМА 1. ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ВЕРОЯТНОСТЕЙ. КЛАССИЧЕСКОЕ ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ
В рекомендованных учебниках по этой теме даны основные понятия теории вероятностей: «испытание», «исход испытания», «событие». Даны определения достоверного, невозможного и случайного событий. Приведена классификация случайных событий: совместные и несовместные, противоположные, равновозможные и единственно возможные события.
Понятие вероятности события – одно из основных понятий в теории вероятности. Оно выражает меру объективной возможности наступления события. В учебниках даны классическое и статистическое определения вероятности события.
Согласно классическому определению, вероятность события А
вычисляется по формуле Р(А) = |
m |
, где n – число всех равновозможных, |
|
n |
|||
|
|
единственно возможных и несовместных исходов испытания, m – число исходов, благоприятствующих появлению события А. Таким образом, нахождение вероятности события сводится к вычислению значений параметров n и m, а так как 0 ≤ m ≤ n, то 0≤ Р(А) ≤ 1.
Пример 1. Имеется 100 одинаковых деталей, среди которых 3 бракованных. Найти вероятность того, что взятая наудачу деталь окажется без брака.
Решение. В этой задаче производится испытание – извлекается одна деталь. Число всех исходов испытания равно 100, т.к. может быть взята любая деталь из 100. Эти исходы несовместны, равновозможны и единственно возможны. Таким образом, n=100. Событие А состоит в появлении детали без брака. Всего в партии 97 деталей без брака, следовательно, число исходов, благоприятных появлению события А равно
97. Итак, m=97. Тогда Р(А)=10097 = 0,97.
При непосредственном вычислении вероятности события А часто для подсчёта числа всех исходов n и числа m, благоприятных событию А исходов, применяются формулы комбинаторики. Приведём краткие сведения из комбинаторики.
Правило произведения. Если объект А может быть выбран n1 способами и после каждого такого выбора объект В может быть выбран n2 способами, то выбор пары А и В может быть осуществлен n1 n2 способами. Это правило распространяется и на случай выбора трёх, четырёх и т.д. объектов.
Пусть дано множество из n элементов.

Размещения. Размещениями из n элементов по m (m ≤ n) называют такие подмножества, каждое из которых содержит m элементов из данных n и которые отличаются друг от друга либо составом элементов, либо их порядком. Число таких подмножеств равно
Аnm = n(n-1) (n-2) …[n-(m-1)] = |
|
n! |
. |
(n |
|
||
|
m)! |
||
Пример 2. Код банковского сейфа состоит из 6 цифр. Найти вероятность того, что наудачу выбранный код содержит различные цифры?
Решение. Так как на каждом из шести мест в шестизначном номере может стоять любая из десяти цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, то всех различных шестизначных номеров по правилу произведения будет n=10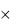 10 10 10 10 10 = 106. Номера, в которых все цифры различны, – это размещения из 10 элементов (10 цифр) по 6. Поэтому число благоприятствующих исходов m= А106 . Искомая вероятность равна
10 10 10 10 10 = 106. Номера, в которых все цифры различны, – это размещения из 10 элементов (10 цифр) по 6. Поэтому число благоприятствующих исходов m= А106 . Искомая вероятность равна
|
|
А6 |
|
10 |
9 |
8 |
7 |
6 |
5 |
|
|
Р(А) = |
|
10 |
= |
|
|
|
|
|
|
|
= 0,151 2 . |
106 |
|
|
|
106 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|||
Перестановки. Перестановками из n элементов называют такие множества, каждое из которых содержит данные n элементов и которые отличаются друг от друга порядком элементов, число перестановок Рn = n!.
Пример 3. Между 6 фирмами: А, Б, В, С, Д, Е, занимающимися продажей компьютерной техники, проводится жеребьёвка на предмет очередности представления своей продукции на выставке потенциальным потребителям. Какова вероятность того, что очередь будет выстроена по порядку, т.е. А, Б, В, Г, Д, Е?
Решение. Исход испытания – случайное расположение фирм в очереди. Число всех возможных исходов равно числу всех перестановок из шести элементов (фирм), т.е. n=Р6=6!. Число исходов, благоприятствующих событию L, – очередь выстроена по порядку: m=1.
Тогда Р(L) = |
1 |
= |
|
|
|
|
1 |
|
|
= 0,0014. |
|
6! |
1 |
2 |
3 |
4 |
5 |
6 |
|||||
|
|
|
|||||||||
Сочетания. Сочетаниями из n элементов по m называют такие подмножества, каждое из которых содержит m элементов из данных n и которые отличаются друг от друга составом элементом
С m = |
n! |
|
. |
|
|
||
|
|
||
n |
m!(n |
m)! |
|
|
|||

Пример 4. В компании 10 акционеров, из них три имеют привилегированные акции. На собрание акционеров явилось 6 человек. Найти вероятность того, что среди явившихся акционеров:
а) все трое акционеров с привилегированными акциями отсутствуют; б) двое с привилегированными акциями.
Решение: 1. Испытанием является отбор 6 человек из 10 акционеров. Число всех исходов испытания равно числу сочетаний из 10 по 6, т.е.
n = С106 = |
10! |
= |
7 |
8 |
9 |
10 |
= 210 . |
||
6! |
4! |
1 |
2 |
3 |
4 |
||||
|
|
|
|||||||
Пусть событие А – среди шести человек нет ни одного с привилегированными акциями. Исход, благоприятствующий событию А, – отбор шести человек среди семи акционеров, не имеющих привилегированных акций. Число всех исходов, благоприятствующих
событию А, будет m = С76 |
= |
7! |
|
= 7. Искомая вероятность равна |
||||||
|
|
|||||||||
|
|
|
|
|
|
|
|
6! |
1! |
|
Р(А) = |
m |
= |
7 |
= |
|
1 |
. |
|
|
|
|
|
|
|
|
|
|||||
|
n |
|
210 |
30 |
|
|
|
|
||
2. Пусть событие В – среди шести явившихся акционеров двое с привилегированными акциями, а остальные четыре – с общими акциями.
Число всех исходов n=С106 = 210. Число способов выбора двух человек из
необходимых трёх m1 = С32 |
= |
3! |
|
= 3. Число способов выбора |
|
|
|||
|
|
2! |
1! |
|
оставшихся четырёх акционеров среди семи с общими акциями m2= C74 =
7! |
= |
5 |
6 |
7 |
= 35. Тогда число всех способов отбора по правилу |
|
4!3! |
1 |
2 |
3 |
|||
|
|
произведения m=m1 m2 = 3 35=105.
Искомая вероятность равна Р(В) = mn = 105210 = 0,5.
ТЕМА 2. КЛАССИЧЕСКИЕ ТЕОРЕМЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
1. Теорема сложения вероятностей
Перед изучением данной темы студенту рекомендуется изучить следующие вопросы: совместность и несовместность событий, сумма событий, теоремы сложения совместных и несовместных событий, полная группа событий, противоположные события.
Вероятность суммы двух событий вычисляется по формуле

Р(А+В) = Р(А) + Р(В) (в случае, если события А и В несовместны); Р(А+В) = Р(А) + Р(В) – Р(А В) (если А и В совместны).
Пример 1. Согласно прогнозу метеорологов, Р(дождь)=0,4; Р(ветер)=0,7; Р(дождь и ветер)=0,2. Какова вероятность того, что будет дождь или ветер?
Решение. По теореме сложения вероятностей и в силу совместности предложенных событий имеем Р(дождь, или ветер, или то и другое) = Р(дождь) + Р(ветер) – Р(дождь и ветер) = 0,4 + 0,7 – 0,2 = 0,9.
2. Теорема умножения вероятностей
Перед изучением данной темы студенту необходимо изучить следующий материал: зависимость и независимость событий, произведение событий, теоремы умножения зависимых и независимых событий, вероятность появления хотя бы одного события.
Вероятность произведения двух событий вычисляется по формуле Р(А В) = Р(А) Р(В) (в случае, если события А и В независимы); Р(А В) = Р(А) РА (В) (если А и В зависимы).
Пример 2. На станции отправления имеется 8 заказов на отправку товара: пять – внутри страны, а три – на экспорт. Какова вероятность того, что два выбранных наугад заказа окажутся предназначенными для потребления внутри страны?
Решение. Событие А – первый взятый наугад заказ – внутри страны. Событие В – второй тоже предназначен для внутреннего потребления. Нам необходимо найти вероятность Р(А В). Тогда по теореме об умножении вероятностей зависимых событий имеем
Р(А В)=Р(А) РА(В) = |
5 |
|
4 |
= |
|
5 |
. |
|
8 |
7 |
14 |
||||||
|
|
|
||||||
Пример 3. Из партии изделий товаровед наудачу отбирает изделия высшего сорта. Вероятность того, что выбранная вещь окажется высшего
сорта равна 0,8; первого сорта – 0,7; |
второго сорта – 0,5. |
Найти |
||
вероятность того, что из трех наудачу отобранных изделий будут: |
|
|||
а) только два высшего сорта; |
|
|
|
|
б) все разного сорта. |
|
|
|
|
Решение. |
Пусть событие А1 |
– |
изделие высшего |
сорта; |
событие А2 – изделие первого сорта; событие А3 – изделие второго сорта. По условию задачи Р(А1)=0,8, Р(А2)=0,7, Р(А3)=0,5. События
А1,А2,А3 – независимы.
1. Событие А – только два изделия высшего сорта будет выглядеть
так: А = А1А1А2 + А1А1А3, тогда
Р(А) = Р(А1А1А2+А1А1А3) = Р(А1) Р(А1) Р(А2)+
+ Р(А1) Р(А1) Р(А3)= (0,8)2 0,7 + (0,8)2 0,5 = 0,768.
