5172
.pdfМинистерство образования и науки Российской Федерации Федеральное агентство по образованию
Государственное образовательное учреждение высшего
профессионального образования
«Хабаровская государственная академия экономики и права»
Кафедра математики и математических методов в экономике
Е.В. Кудрявцева Е.Н. Кравченко
Высшая математика Программа, методические указания, варианты контрольной работы № 2
для студентов 1-го курса заочной формы обучения
Хабаровск 2008
2
ББК В 11
Х 12
Высшая математика : программа, методические указания, варианты контрольной работы № 2 для студентов 1-го курса заочной формы обучения / сост. Е. В. Кудрявцева, Е. Н. Кравченко. – Хабаровск : РИЦ ХГАЭП, 2008. – 36 с.
В методических указаниях подобраны примеры для самостоятельного выполнения студентами контрольной работы № 2. Подробно разобрано решение типовых задач.
Методические указания предназначены для студентов заочной формы обучения всех специальностей.
Рецензент канд. физ.-мат. наук, доцент, начальник отделения подготовки научно-педагогических кадров ХПИ ФСБ России Ивлева А.И.
Утверждено издательско-библиотечным советом академии в качестве методических указаний
Кравченко Елена Николаевна
Кудрявцева Елена Викторовна
Высшая математика
Программа, методические указания, варианты контрольной работы № 2
для студентов 1-го курса заочной формы обучения
Редактор Г.С.Одинцова
Подписано в печать |
Формат 80×64/16. |
Бумага писчая. |
|
Печать офсетная. |
Усл.п.л. |
Уч.-изд.л. |
Тираж 300 экз. |
Заказ № |
|
|
|
680042, Хабаровск, ул.Тихоокеанская, 134, ХГАЭП, РИЦ
© Хабаровская государственная академия экономики и права, 2008
3
Введение
Математика играет важную роль в естественнонаучных, инженерно-
технических и гуманитарных исследованиях. В то же время математика является не только мощным средством решения прикладных задач и универсальным языком науки, но также элементом общей культуры. Поэтому математическое образование следует рассматривать как важнейшую составляющую в системе фундаментальной подготовки современного экономиста.
Данные методические указания содержат рабочую программу по высшей математике, методические указания к отдельным разделам программы, варианты контрольной работы № 2.
Предусматриваются задания по следующим темам: «Предел функции», «Производная и дифференциал», «Исследование функций и построение графиков», «Применение понятия производной в экономике», «Интегралы».
Изучив теоретический материал согласно прилагаемой программе, необходимо выполнить контрольную работу в сроки, указанные в вашем учебном графике.
4
ПРОГРАММА КУРСА МАТЕМАТИКИ
1.Функция одной переменной. Область определения функции. Способы задания. Основные элементарные функции, их графики. Монотонность функции, ограниченность функции. Обратные и сложные функции.
2.Числовая последовательность. Предел числовой последовательности.
Теоремы о единственности предела числовой последовательности, об ограниченности последовательности, имеющей предел. Бесконечно малые величины. Теоремы о бесконечно малых. Бесконечно большие величины. Связь между бесконечно малыми и бесконечно большими величинами. Теорема о связи переменой, ее предела и бесконечно малой.
Предел суммы, произведения, частного. Предельный переход в неравенствах. Признак существования предела монотонной последовательности. Предел функции. Теорема о пределе функции.
Раскрытие неопределённостей. Первый замечательный предел. Второй замечательный предел. Сравнение бесконечно малых. Эквивалентные бесконечно малые и их применение для вычисления пределов.
3.Непрерывность функции в точке, на интервале. Непрерывность сложной
и обратной функции. Точки разрыва функции, свойства функций,
непрерывных на [a,b].
4.Производная y = f(x). Геометрический смысл производной. Уравнение касательной. Теорема о непрерывности функции, имеющей производную.
Производная суммы, произведения, дроби. Производные тригонометрической функции, показательной функции, степенной функции, обратных тригонометрических функций. Производные обратной и сложной функции. Производные высших порядков.
Дифференциал. Геометрический смысл дифференциала.
5.Теорема Ферма. Теоремы Ролля, Лагранжа, их геометрический смысл.
Правило Лопиталя. Признак возрастания (убывания) функции на
интервале. Экстремум функции |
y = f(x). Необходимое условие |
экстремума. Второе достаточное условие экстремума. Наименьшее и
5
наибольшее значение y = f(x) на [a,b]. Выпуклость, вогнутость, точки
перегиба. Асимптоты кривых. Вертикальные и наклонные асимптоты.
6.Функции нескольких переменных. Область определения. Способы задания. Понятие предела для функции двух переменных. Непрерывность функции Z = f(x,y). Частные приращения, частные производные. Полное приращение, полный дифференциал Z = f(x,y). Экстремум функции двух переменных. Метод наименьших квадратов.
7.Первообразная функции. Теорема о первообразных. Определение неопределённого интеграла. Свойства неопределённого интеграла.
Замена переменной в неопределённом интеграле. Интегрирование по частям. Интегрирование рациональных дробей, тригонометрических выражений, иррациональных функций. Задача о площади криволинейной трапеции. Интегральная сумма. Определённый интеграл. Свойства определённого интеграла. Определённый интеграл с переменным верхним пределом. Формула Ньютона-Лейбница. Замена переменной в определённом интеграле. Площадь плоской фигуры. Несобственные интегралы.
8.Числовой ряд. Сходимость числового ряда. Свойства рядов.
Геометрический ряд. Гармонический ряд. Необходимый признак.
Признак сравнения. Признак Даламбера. Интегральный признак.
Знакочередующийся ряд. Признак Лейбница. Степенной ряд. Радиус сходимости степенного ряда. Ряд Маклорена. Условия разложимости в ряд. Ряды Маклорена для y=sinx, y=cosx, y=(1+x)m. Приближённые вычисления с помощью рядов.
КОНТРОЛЬНЫЕ ЗАДАНИЯ, ПРАВИЛА ВЫПОЛНЕНИЯ И ОФОРМЛЕНИЯ КОНТРОЛЬНОЙ РАБОТЫ
Вариант для контрольного задания студент выбирает в соответствии с двумя последними цифрами своего шифра по следующему правилу: вторая цифра номера варианта должна совпадать с последней цифрой шифра. Далее,
если предпоследняя цифра шифра чётная, то первая цифра номера варианта должна быть равна 0 или 2; если же предпоследняя цифра нечётная, то первая
6
цифра номера варианта должна быть 1. Например, при учебном номере (шифре) 955027 студент решает 07 вариант, при шифре 953054 – вариант 14 и т.д.
Номера |
|
Номера задач |
для контрольного задания |
|
||||
вариантов |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
01 |
1 |
21 |
41 |
|
61 |
81 |
|
101 |
02 |
2 |
22 |
42 |
|
62 |
82 |
|
102 |
03 |
3 |
23 |
43 |
|
63 |
83 |
|
103 |
04 |
4 |
24 |
44 |
|
64 |
84 |
|
104 |
05 |
5 |
25 |
45 |
|
65 |
85 |
|
105 |
06 |
6 |
26 |
46 |
|
66 |
86 |
|
106 |
07 |
7 |
27 |
47 |
|
67 |
87 |
|
107 |
08 |
8 |
28 |
48 |
|
68 |
88 |
|
108 |
09 |
9 |
29 |
49 |
|
69 |
89 |
|
109 |
10 |
10 |
30 |
50 |
|
70 |
90 |
|
110 |
11 |
11 |
31 |
51 |
|
71 |
91 |
|
111 |
12 |
12 |
32 |
52 |
|
72 |
92 |
|
112 |
13 |
13 |
33 |
53 |
|
73 |
93 |
|
113 |
14 |
14 |
34 |
54 |
|
74 |
94 |
|
114 |
15 |
15 |
35 |
55 |
|
75 |
95 |
|
115 |
16 |
16 |
36 |
56 |
|
76 |
96 |
|
116 |
17 |
17 |
37 |
57 |
|
77 |
97 |
|
117 |
18 |
18 |
38 |
58 |
|
78 |
98 |
|
118 |
19 |
19 |
39 |
59 |
|
79 |
90 |
|
119 |
20 |
20 |
40 |
60 |
|
80 |
100 |
|
120 |
|
|
|
|
|
|
|
|
|
При выполнении контрольной работы надо строго придерживаться указанных ниже правил. Работы, выполненные без соблюдения этих правил, не зачитываются и возвращаются студентам для переработки.
1.Контрольные работы выполнять в тетради пастой или чернилами любого цвета, кроме красного, оставляя поля для замечаний рецензента.
2.На обложке тетради должны быть ясно написаны фамилия студента, его инициалы, шифр, название дисциплины и номер контрольной работы; здесь же следует указать дату отсылки работы в академию и почтовый адрес студента.
3.В работу должны быть включены все задачи, указанные в задании, строго по своему варианту. Контрольные работы, содержащие не все задания, а также содержащие задачи не своего варианта, не зачитываются.
4.Решение задач надо располагать в порядке, указанном в заданиях, сохраняя номера задач.
5.Перед решением каждой задачи надо выписать полностью её
7
условие. Если несколько задач имеют общую формулировку, следует,
переписывая условие задачи, заменить общие данные конкретными из соответствующего номера.
6.После получения отрецензированной работы (как зачтённой,
так и незачтённой) студент должен исправить в ней все отмеченные рецензентом ошибки и недочёты. В связи с этим следует оставлять в конце тетради чистые листы для работы над ошибками. Вносить исправления в сам текст работы после её рецензирования запрещается.
7.Выполнив работу над ошибками, необходимо выслать работу в
кротчайший срок.
8.В конце работы следует указать литературу, которую изучал студент,
выполняя данную работу.
9.Студент должен подписать работу и поставить дату.
10.Зачтённые контрольные работы вместе с рецензиями обязательно
предъявляются на зачёте и экзамене.
11.Перед сдачей зачёта и экзамена студент обязан защитить контрольную работу.
Библиографический список
1.Карасев А. И., Аксютина З. М., Савельева Т. К. Курс высшей математики
для экономических вузов. Ч. 1. – М. :Высшая школа, 1982.
2.Лихолетов И. И. Высшая математика, теория вероятностей и
математическая статистика. – Минск : Вышейшая школа, 1976.
3.Минорский В. П. Сборник задач по высшей математике. – М. : Наука, 1977.
4.Лихолетов И. И., Мацкевич И. П. Руководство к решению задач
по высшей математике, теории вероятностей и математической статистике. –
Минск : Вышейшая школа, 1976.
5.Высшая математика для экономистов : учеб. пособие / под ред. Н. Ш. Кремера. – М. : Банки и биржи, 1997.
6.Красс М. С. Чупрынов Б. П. Основы математики и её проложение в экономическом образовании. – М. : Дело 2001.
8
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
Предел функции
Пусть функция y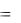 
ƒ(x) задана в некоторой окрестности точки х0.
Определение. Число А называется пределом функции f(x) в точке X0 (или при х→х0), если для любого, сколь угодно малого положительного числа ε>0
найдётся такое положительное число δ>0, зависящее от ε, что для всех х,
удовлетворяющих условию 0< |
x x0 |
, |
выполняется |
неравенство |
|||
|
f (x) A |
|
. Этот предел функции обозначается: |
lim f (x) |
A или ƒ(х)→А |
||
|
|
||||||
|
|
|
|
|
|
x x0 |
|
при х→х0. |
|
|
|
|
|
||
Практическое вычисление пределов основывается на следующих теоремах.
Если существуют |
lim f (x) |
lim g(x) |
и , то |
|
|
x a |
x |
a |
|
1) lim [ f (x) |
g(x)] |
lim f (x) |
lim g(x) ; |
|
x a |
|
x |
a |
x a |
2) lim [ f (x) g(x)] |
lim f (x) |
x a |
x a |
3) |
lim [cf (x)] |
c |
lim f (x) ; |
|||||
|
x |
a |
|
|
|
x a |
|
|
|
|
|
f (x) |
|
lim f (x) |
|
||
4) |
lim |
x |
a |
(при |
||||
g(x) |
lim g(x) |
|||||||
|
x |
a |
|
|||||
|
|
|
|
|
x |
a |
|
|
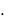lim g(x) ;
x a
lim g x 0 ).
x a
Используются также следующие пределы:
lim |
sin x |
|
1 (первый замечательный предел); |
|||
|
||||||
x 0 |
x |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
x |
(второй замечательный предел). |
|
|
|
1 |
|
|||
|
|
|
||||
|
|
|
|
|||
lim |
1 |
|
|
lim 1 |
|
e 2,71828 |
x |
|
|||||
x |
|
0 |
|
|
||
|
|
|
|
|
||
Определение. Функция α (х) называется бесконечно малой величиной при х→х0, или при х→∞, если её предел равен нулю:
lim (x) 0 x x0
Определение. Функция ƒ(х) называется бесконечно большой в точке х0
9
(или при х→х0), если имеет место одно из равенств:
lim f (x) |
|
; |
|
|
|
|
lim f (x) |
; |
lim f (x) |
|||||
x x0 |
|
|
|
|
|
|
|
x |
x0 |
|
x |
x0 |
|
|
При вычислении пределов также используется следующее утверждение. |
||||||||||||||
Если ƒ(х) – бесконечно малая функция при х→х0, то |
1 |
– бесконечно большая |
||||||||||||
|
||||||||||||||
f (x) |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
функция при х→х0, и наоборот. |
|
|
|
|
||||||||||
Пример1. |
lim |
2x |
4 |
|
Поскольку функция непрерывна в точке х=7, искомый |
|||||||||
|
|
x |
5 |
|
||||||||||
|
x |
7 |
|
|
|
|
|
|
|
|
|
|||
предел равен значению функции в этой точке. |
Используя теоремы о пределах |
|||||||||||||
суммы, разности, частного, получим |
|
|
|
|
||||||||||
lim |
2x |
4 |
|
2 7 |
4 |
9 . |
|
|
|
|
||||
x |
5 |
|
7 |
|
5 |
|
|
|
|
|||||
x 7 |
|
|
|
|
|
|
|
|||||||
Пример 2. |
lim |
|
2x |
5 |
|
|
|
|
|
|
|
|||
|
|
x |
5 |
|
|
|
|
|
|
|
||||
|
x |
5 |
|
|
|
|
|
|
|
|
|
|||
При х→5 числитель (2х + 5) стремится к 2 ∙ 5 + 5 = 15 (т.е. является ограниченной функцией), а знаменатель (х – 5) – к нулю (т.е. является бесконечно малой величиной), очевидно, их отношение есть величина
бесконечно большая, т.е. lim |
2x |
5 |
. |
|
x |
5 |
|||
x 5 |
|
Врассмотренных примерах предел находился сразу: в виде числа или символа
∞.Но чаще при вычислении пределов мы сталкиваемся с неопределённостями,
когда результат нахождения предела не ясен, например, в случае отношения
двух бесконечно малых функций |
0 |
|
или бесконечно больших |
|
|
|
. |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
0 |
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Пример 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
3(x 3)(x |
1 |
) |
|
|
|
|
|
|
|
|
|
|
||
|
3x 2 |
|
10x 3 |
0 |
|
|
|
|
|
|
|
|
|
3x 1 |
|
8 |
|
|||||||
lim |
|
|
lim |
3 |
lim |
|
|
. |
||||||||||||||||
|
3 |
|
|
0 |
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
27 |
||||||
x 3 x |
27 |
|
x 3 |
(x 3)(x |
3x 9) x 3 x |
|
3x |
9 |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||
10
Пример 4
|
|
x 2 |
|
|
|
|
|
|
(x 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
(x 2 |
|
|
|
|
||||||
lim |
25 |
|
|
0 |
|
lim |
25)(2 |
|
x |
1) |
|
|
|
lim |
25)(2 |
|
x 1) |
||||||||||||||||
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
(x |
1) |
|
|||||||||
2 |
|
x 1 |
|
(2 |
|
x |
1)(2 |
|
|
x |
1) |
|
|
|
|||||||||||||||||||
x |
5 |
|
|
x |
5 |
|
|
|
|
x 5 |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
(x |
5)(x |
5)(2 |
|
x |
1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
lim |
|
|
lim (x |
5)(2 |
|
|
|
x |
1) |
10 |
4 |
40. |
|
|
|
||||||||||||||||||
|
|
|
(x 5) |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
x |
5 |
|
|
|
|
|
|
|
|
x |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Пример 5.
lim |
2x 2 |
3x |
4 |
|
|
. Теорему о пределе частного здесь применить |
|
|
|
|
|
|
|
||
|
x 4 |
|
|
||||
x |
|
1 |
|
|
|
||
нельзя, так как числитель и знаменатель дроби конечного предела не имеют. В
данном случае имеем неопределённость вида . Разделим числитель и
знаменатель дроби на высшую степень х (в данном случае на х2 ), а затем воспользуемся теоремами о пределах функций:
|
|
|
|
|
|
|
2x 2 |
|
3x |
4 |
|
|
|
|
|
|||||||
lim |
2x 2 |
3x 4 |
lim |
x 2 |
|
x 2 |
|
x 2 |
|
2 |
2 . |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
||||||
|
x 4 |
|
|
|
|
|
x 4 |
|
|
|
|
|
|
|
||||||||
x |
|
1 |
x |
|
|
|
|
1 |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
x 4 |
x 4 |
|
|
|
|
|
||||||
Здесь мы |
воспользовались |
следующим |
равенством: lim |
a |
0 (а – любое |
|||||||||||||||||
x |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
||
число).
Производная и дифференциал
Пусть функция у = f(x) определена на промежутке X. Возьмём точку х Х.
Дадим значению х приращение x 0 , тогда функция получит приращение y f x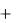 
x
f x .
Определение 1. Производной функции у = f(x) называется предел отношения приращения функции к приращению независимой переменной при стремлении последнего к нулю (если этот предел существует):