§ 9. Исследование функций и построение графиков

Учиться строить графики по результатам исследования функций лучше всего на занятиях вместе с группой. Возможны разные способы построения графика по уже проведённому исследованию, например,

– постепенное уточнение: «монотонность – выпуклость – асимптоты»;

– уточнение: «поведение на краях – асимптоты – монотонность – выпуклость»;

– соединение отрезков, на которых ничего не меняется (выпуклое убывание, выпуклое возрастание и т.д. – метод, популярный в средней школе).

Общая схема исследования функции

1) Элементарное исследование:

а) найти область определения (обязательно), область значений;

б) точки пересечения с осями координат;

в) чётность и (или) периодичность;

2) Монотонность и экстремум:

а) найти корни производной и разместить их на числовой оси;

б) выяснить знак производной на каждом полученном интервале;

в) определить интервалы возрастания, убывания;

г) найти точки минимума и максимума;

3) Выпуклость и перегиб:

а) найти 2-ю производную, найти её корни и расставить их на числовой оси;

б) – г) по аналогии с 2) определить интервалы выпуклости «вниз», «вверх»,

точки перегиба;

4) асимптоты графика (для многочленов этот шаг не имеет смысла);

5) график функции строится по всем особенным точкам и линиям, полученным

на предыдущих шагах.

Замечание 1. Под точкой минимума или перегиба подразумевается как абсцисса (значение переменной), так и ордината (значение функции в этой переменной). Таким образом, речь идёт о точках графика, а не точках числовой оси. В литературе в этом отношении часто встречаются противоречия в текстах.

Исследование на выпуклость обычно связано с вычислительными трудностями. Далее показано, как при помощи небольшого рассуждения упростить построение графика, обходясь без 2-й производной.

Пример 1. Посмотрим, как можно построить график функции .

Замечаем, что функция не пересекает ось OX (уравнение не имеет корней). Кроме того, функция чётная – значит, график симметричен относительно оси OY.

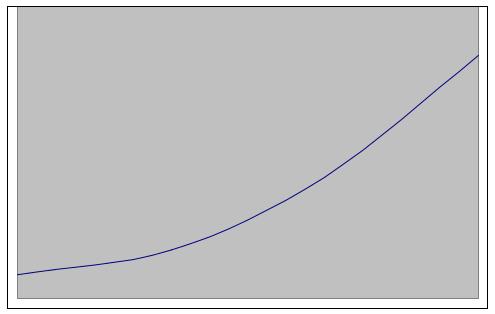
С ростом x от до 0 величина убывает от до 1. Обратная к ней величина соответственно возрастает от до :

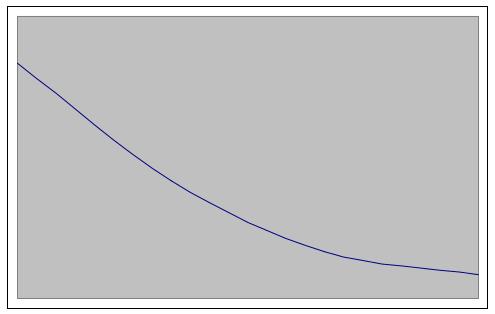
С другой стороны, растёт от 1 при до при , тогда обратная величина убывает от при до при :

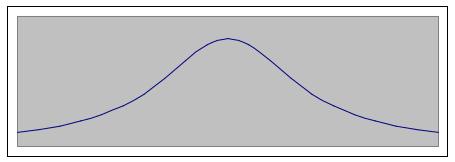
Подтверждается замечание о симметричности графика относительно вертикали. Объединяя графики, получаем такой набросок:

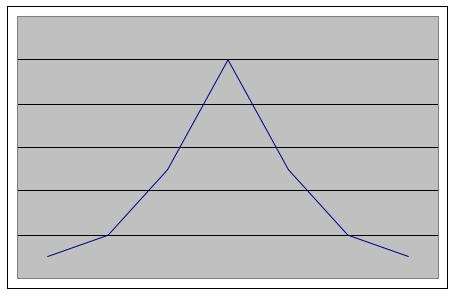
Однако график должен быть плавный, поскольку 1-я произ­водная определена во всех точках. Поэтому с каждой стороны от оси OY график обязательно перегнётся:
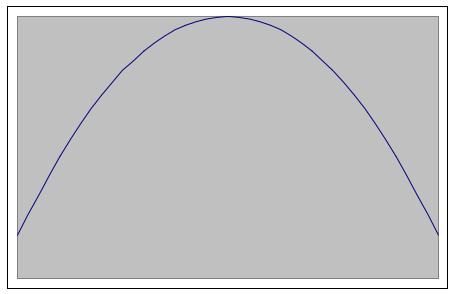
Здесь решающую роль сыграло то, что график не пересекает ось OX. Иначе была бы возможна любая ситуация, например, такая:

Пример 2. Функция нечётная, и её график симметричен относительно начала координат. Посмотрим, что происходит при . Заметим, что график пересекает ось OX в точке , и только в ней.

При функция , не пересекая ось OX. Также при функция положительна. Получается, что где-то при функция достигает максимума, и потом убывает:
Но если функция будет выпукла вверх, она пересечёт ось OX при , а этого быть не должно. Значит, где-то после точки максимума график перегнётся и пойдёт выпуклостью вниз:

Учитывая симметрию относительно начала координат, получаем примерно такой график: Здесь центр рисунка соответствует началу координат.

Поиск производных нужен, если интересуют конкретные координаты точек экстремума или перегиба. Кроме того, приведённые рассуждения определяют число точек экстремума или перегиба с точностью до чётного числа.

Так, в примере 2 при могла быть не 1, а 3 точки перегиба (но не 2 и не 4!), не 1 максимум, а 2 максимума и 1 минимум между ними, и т.д.

Замечание 2. В строгой математической литературе нередко «выпуклая функция» – это функция, график которой обращён «выпуклостью вниз» (например, парабола). Соответственно функции типа квадратного корня оказываются «вогнутыми». Это противоположно студенческой (и преподавательской) традиции, поэтому при обращении к старым учебникам необходимо внимательно следить, о каких функциях речь.

ИФ1. Постройте графики квадратичных функций по стандартной схеме исследования. Сравните с тем, что получается при построении по школьной схеме:

1) ;

2) ;

Примечание: Школьная (элементарная) схема – это поиск вершины параболы, точек пересечений с осями координат и определение направления ветвей.

ИФ2. Исследуйте функции и постройте графики многочленов:

1) ;

2) ;

3) ;

4) .

ИФ3. Исследуйте функции, упростив производные, и постройте графики:

1) ;

2) .

Пояснение: Производную в ИФ3 удобно найти, не раскрывая скобок:

.

Здесь применена формула .

Для поиска корней 1-й производной, а затем для поиска 2-й производной скобки лучше раскрыть:

.

ИФ4. Исследуйте дробно-рациональные функции и постройте их графики:

1) ;

2) ;

3) ;

4) ;

5) ;

6) ;

7) ;

8) ;

9) ;

10) ;

11) ;

12) ;

13) .

ИФ 5. Постройте графики функций

1) ;

2) ;

3) .