III. Производная и исследование функций
§ 6. Основы дифференцирования функций
Производная от
функции
– это предел
,
или, что то же самое,
.
Производная показывает, во сколько раз
(вблизи точки x)
функция меняется быстрее, чем аргумент.
Значение производной
в точке
– это число, обозначаемое
.
Производная в общем виде – это новая
функция, обозначаемая как
.
Возможны также обозначения
или
,
если
.
Замечание 1. Значение производной зависит от единиц измерения аргумента и функции. Например, если цену измерять в рублях, скорость изменения спроса будет в 100 раз выше, чем при измерении цены в копейках. Этим производная отличается от таких понятий, как эластичность, темп прироста, относительный прирост, и некоторых других, применяемых в экономических приложениях.
Производные от основных элементарных функций
1)
;
2)
; 3)
;
4)
; 5)
; 6)
;
7)
.
Во 2-й и 3-й формулах
и
.
Полезно запомнить частные случаи:
;
(поскольку
).
Производные других функций получают на основе правил дифференцирования.
Основные правила дифференцирования (в сокращённой записи):
1)
; 2)
для любого
;
3)
; 4)
.
Производная
сложной функции. Если
даны функции
и
,
то производная сложной функции
,
определённой как
,
обладает свойством
и находится обычно по этой формуле.
На основе этого правила получается
Обобщённая таблица основных производных
1)
;
2)
; 3)
;
4)
; 5)
; 6)
;
7)
,
а также частные случаи, аналогичные приведённым выше.
Как следствия из основных свойств получаются производные
;
.
Правила
дифференцирования отражают объективные
свойства функций и помогают найти
производную наиболее простым образом.
Любая попытка «исправить правило»
(например, решить, что
)
приведёт к противоречию.
ОД1.
Даны функция
,
точка
и приращение аргумента
.
Найдите
и
– значения функции в точках
и
,
приращение функции
и отношение
.
Замечание 2. При решении примеров с чётными номерами (2, 4, 6, 8 и 10) воспользуйтесь результатами примеров 1, 3, 5, 7, 9 соответственно.
1)
;
а)
; б)
; в)
;
г)
; д)
; е)
;
2)
;
а) ; б) ; в) ;
г) ; д) ; е) ;
3)
;
а)
; б)
; в)
;
г)
; д)
; е)
;
4)
;
а) ; б) ; в) ;
г) ; д) ; е) ;
5)
;
а)
; б)
; в)
;
г)
; д)
; е)
;
6)
;
а) ; б) ; в) ;
г) ; д) ; е) ;
7)
;
а)
; б)
; в)
;
г)
; д)
; е)
;
8) ;
а) ; б) ; в) ;
г) ; д) ; е) ;
9)
;
а)
; б)
; в)
;
г)
; д)
; е)
;
10)
;
а) ; б) ; в) ;
г) ; д) ; е) .
Замечание
3. В примерах
9 и 10 число 2 добавлено во избежание
деления на 0 в примере 10. На величину
в примере 9 оно не влияет.
Пример
1а. Пусть
,
,
тогда
а)
; б)
;
в)
; г)
;
д)
(значение точное).
Пусть теперь , но по-прежнему , тогда
а)
; б)
;
в)
; г)
;
д)
(обратите внимание на применение знаков точного и приближённого равенства).
Пример
1б. Пусть
,
,
тогда
а)
; б)
;
в)
; г)
;
д)
.
Пусть теперь
при тех же
и
:
а)
; б)
;
в)
; г)
;
д)
.
ОД2.
Найдите производные от суммы, разности,
произведения и частного функций
и
,
а также производные от их линейных
комбинаций
и
:
1) , при этом
а)
; б)
; в)
; г)
;
д)
;
е)
; ж)
; з)
;
2)
,
при этом
а)
; б)
; в)
; г)
;
д)
;
е)
; ж)
; з)
;
3)
,
при этом
а)
; б)
; в)
; г)
;
д)
;
е)
; ж)
; з)
.
Пример 2. Пусть и даны функции
а)
; б)
; в)
.
Найдём
– эта производная понадобится во всех
трёх случаях;
а)
для пары
и
дополнительно находим
,
тогда
;
;
;
;
;
.
Обратите внимание,
что
и
(по таблице производных). Полученные
выше результаты совпадают с табличными;
б)
для пары
и
находим
,
тогда
;
;
;
;
;
;
в)
для пары
и
находим
,
тогда
;
;
;
;
;
.
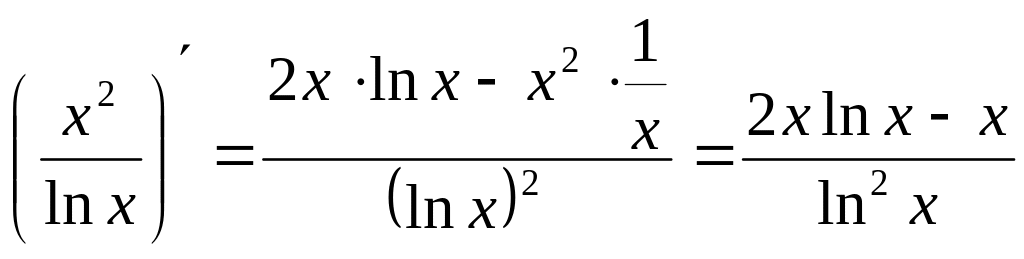ОД3.
Найдите производную функции
,
применив правило
:
а)
; б)
; в)
; г)
;
д)
; е)
; ж)
; з)
.
Пример
3. Напомним,
что
:
а) пусть
,
тогда
;
б) пусть
,
тогда
;
в) пусть
,
тогда
.
ОД3а.
Для функций
из задания ОД3 составьте функцию
,
представьте
как
и найдите производную по правилу
.
Пример 3а. Пусть даны функции
а)
; б)
; в)
; г)
.
Учтём, что
:
а) если
,
то
,
тогда
;
б) если
,
то
,
тогда
;
в) если
,
то
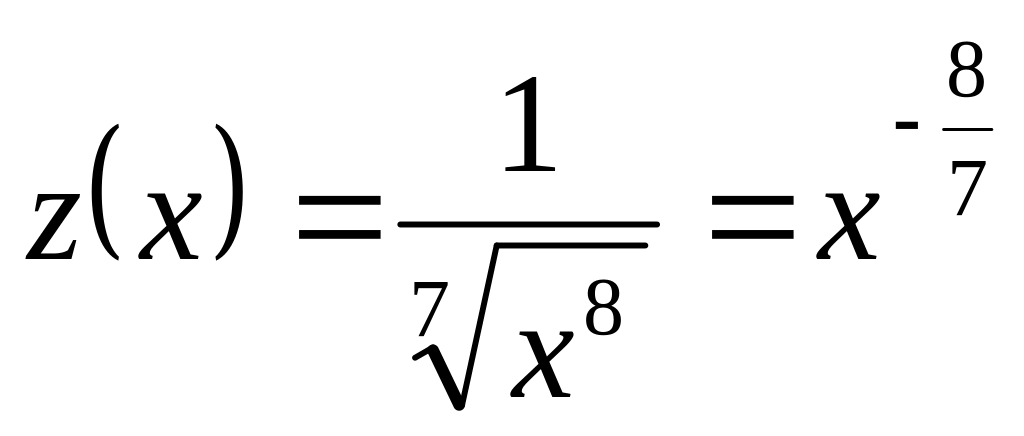и
;
г) если
,
то
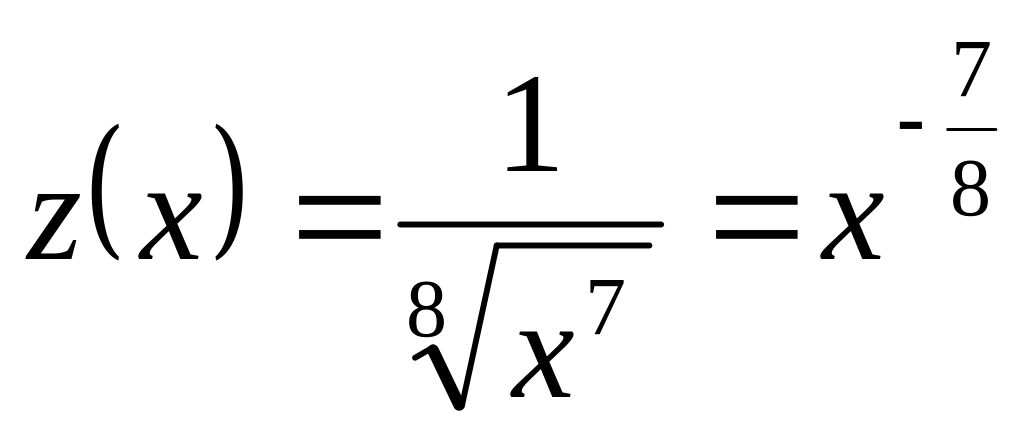и
.
ОД4.
Найдите производную функции
,
зная производную
для функции
и применив правило дифференцирования
:
а)
; б)
; в)
; г)
;
д)
; е)
; ж)
; з)
.
Таким же образом найдите производные для функций задания ОД3 и сравните с уже известными результатами.
Пример 4. Пусть даны функции
а)
; б)
; в)
;
а) если
,
то
,
при этом
и
;
б) если
,
то
,
при этом
и
;
в) если
,
то
,
при этом
и
.
Заметим, что
,
что совпадает с полученной выше
производной. Также
.
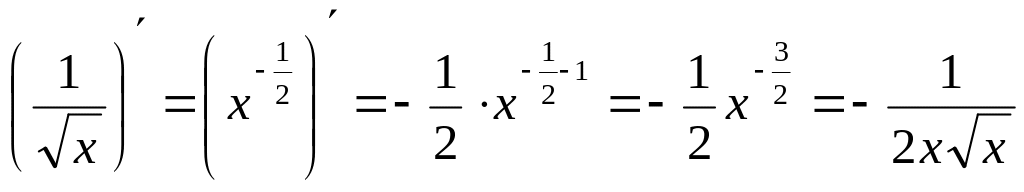Проще и надёжнее искать производные от степенной функции, а не от дроби.
ОД5.
Найдите производную функции
,
если
:
а)
; б)
; в)
; г)
;
д) ; е) ; ж) ; з) .
Пример 5. Воспользуемся указанным выше правилом:
а) пусть
,
тогда
;
б) пусть
,
тогда
;
в) пусть
,
тогда
.
Заметьте, что по свойствам логарифма и по свойствам производной также будет
и
.
ОД6.
Найдите производную функции
по правилу
:
а) ; б) ; в) ; г) ;
д)
; е)
; ж)
; з)
.
Пример 6. По правилу дифференцирования показательной функции:
а) пусть
,
тогда
;
б) пусть
,
тогда
;
в) пусть
,
тогда
.
ОД7.
Применяя свойство логарифма
и правило
,
где
– любое число, продифференцируйте
функцию
:
а)
; б)
; в)
; г)
;
д)
; е)
; ж)
; з)
.
Пример 7. По правилу дифференцирования логарифма некоторой функции
а) если
,
то
,
поэтому
;
б) если
,
то
,
и
;
в) если
,
то
,
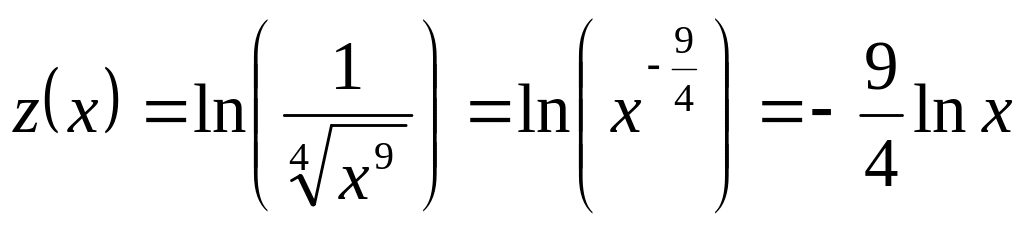поэтому
.
ОД8.
Представив функции
как квадраты, т.е. считая, что
,
где
– некоторая более простая функция,
найдите производные функций
по правилу дифференцирования
:
а)
; б)
; в)
; г)
;
д)
; е)
; ж)
; з)
.
Пример 8. По правилу дифференцирования квадрата некоторой функции
а) если
,
то
;
б) если
,
то
;
в) если
,
то
.
ОД9.
Представив функции
как
,
где
– более простая функция, а
–
некоторый показатель степени (число),
найдите производные функций
по правилу дифференцирования
:
а)
; б)
; в)
; г)
;
д)
; е)
; ж)
; з)
;
и)
; к)
; л)
; м)
.
Пример 9. Найдём производные функций, возведённых в степень:
а) пусть
,
тогда
;
б) пусть
,
или
,
тогда
;
в) если
,
или
,
то
.
ОД10. Задание то же, что в ОД9, но число – дробное:
а)
; б)
; в)
;
г)
;
д)
; е)
;
ж)
; з)
; и)
;
к)
; л)
; м)
.
Пример 10. Продифференцируем функции, стоящие под знаком корня:
а) пусть
,
т.е.
,
тогда
;
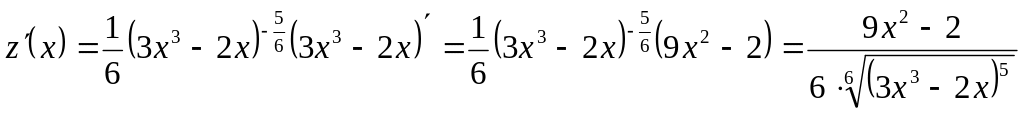б) пусть
,
т.е.
,
тогда
;
в) если
,
т.е.
,
то
.