§ 7. Логарифмическое дифференцирование
Логарифмическое
дифференцирование обычно применяют,
чтобы найти производные от
степенно-показательных
функций
или от произведений
и дробей
,
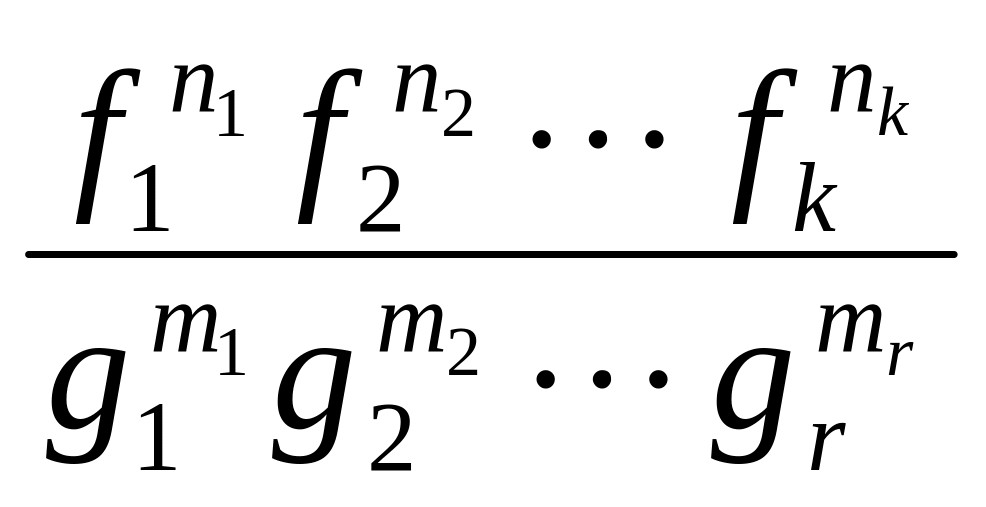где
– действительные числа.
В этих случаях можно найти логарифм функции, упростить его по основным свойствам логарифмов, продифференцировать то, что получилось, и умножить на первоначальную функцию.
Правило
дифференцирования
следует из формулы
.
Пример 1.
Применяя свойство
,
находим
,
тогда
,
т.е.
.
Поэтому
,
или, после раскрытия
скобок,
.
Пример 2.
Здесь
,
тогда
,
поэтому
.
Пример 3. Найдём
производную функции
.
Логарифмируем:
,
выносим степень:
,
дифференцируем:
.
Тогда
.
Пример 4.
Можно раскрыть скобки, привести подобные слагаемые и продифференцировать частное, но лучше найти
и затем
.
Полученную сумму умножим на исходную функцию. Раскрывать скобки нет смысла – наоборот, в таких задачах желательно выносить общий множитель. Итак,
.
Пример 5.
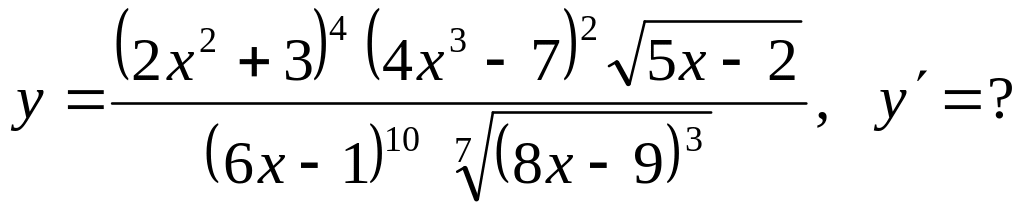
Раскрыть скобки невозможно из-за корней, и непосредственное дифференцирование весьма громоздко. Поэтому ищем
,
затем по свойству логарифма выносим степени:
,
и тогда
.
Окончательно
.
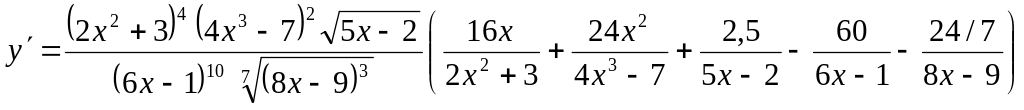ЛД1. Найдите производные функций
1)
;
2)
;
3)
;
4)
;
5)
.
ЛД2. Найдите производные функций при помощи логарифмического дифференцирования. Укажите, в каких точках производная не определена:
1)
;
2)
;
3)
.
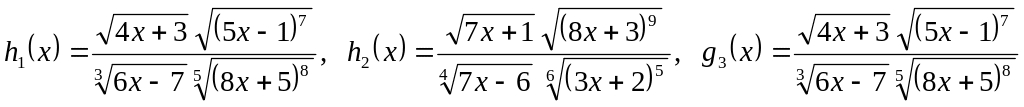ЛД3. Найдите производные при помощи логарифмирования:
1) а)
; б)
;
2) а)
; б)
;
3) а)
; б)
.
Пример 6.
Пусть
,
тогда
,
соответственно
,
и тогда
.
§ 8. Правило Лопиталя – Бернулли
Правило позволяет
раскрывать неопределённости
и
,
а также, после приведения к указанным
дробям, неопределённости
,
,
и
.
Оказывается, если
в некоторой точке две функции равны 0,
то предел их отношения такой же, как у
отношения производных:
.
Подобное свойство
выполнено, если функции в точке a
становятся бесконечно большими:
.
Кроме того, оба
свойства справедливы, когда
,
а не к точке a.
Пример 1.
Найдём
.
Поскольку
и
,
то
.
Разумеется, можно
было вначале сократить
и потом подставить 2.
Пример 2.
.
Пример 3.
(или
)
(если забыть, что
при любых
и
всегда
).
Пример 4. Правило Лопиталя – Бернулли можно применять несколько раз:
.
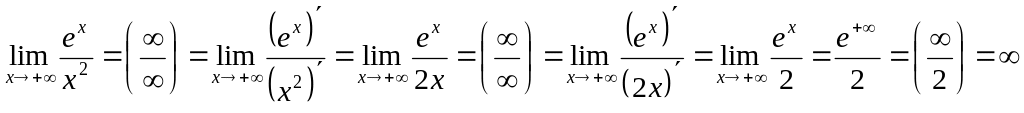(тем самым
при любых
и
,
даже при
и
).
Правило нельзя применять, если нет неопределённости или .
Пример 5.
,
при этом
.
ЛБ1. Найдите по правилу Лопиталя – Бернулли
1) а)
; б)
; в)
; г)
;
2) а)
; б)
; в)
; г)
;
3) а)
; б)
; в)
; г)
;
4) а)
; б)
; в)
; г)
;
5) а)
; б)
; в)
; г)
.
Неопределённость можно раскрыть, заменив на или .
Пример 6.
Найдём
.
Учтём, что
,
тогда
.
Неопределённость
приводят к
,
а затем – к
или
.
Пример 7.
Найдём
.
Преобразуем:
.
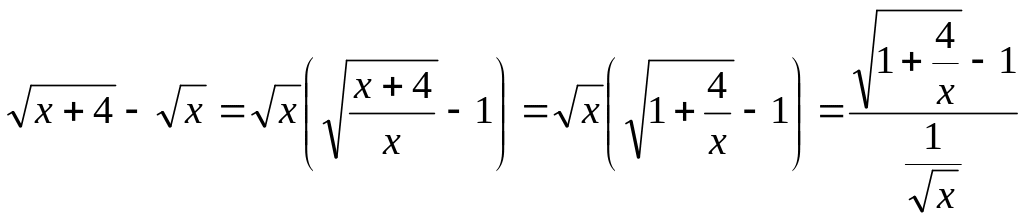Но
,
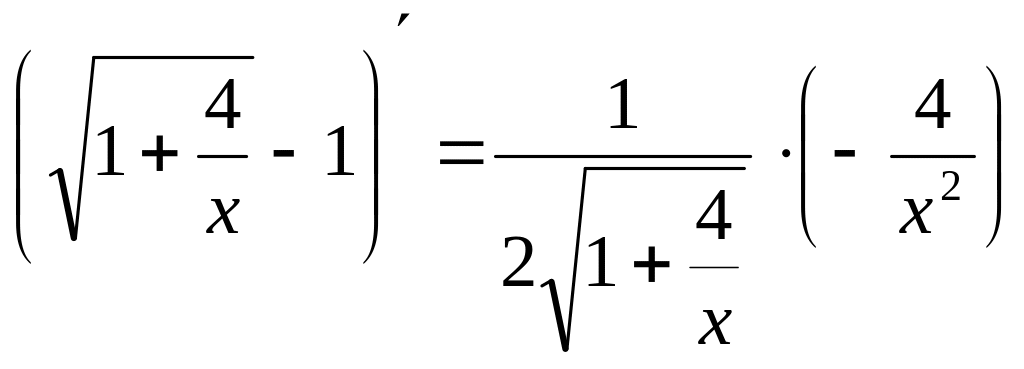и
.
Тогда отношение производных можно
упростить до
.
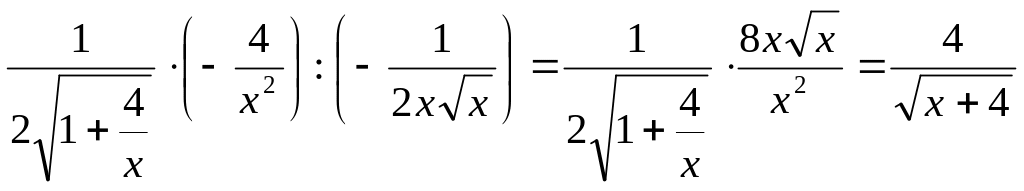Значит,
.
В данном примере
можно было сразу после взятия производных
учесть, что
при
,
и не записывать громоздкий корень, а
заменять числом 1. Однако так нельзя
делать, если из корня такое же число 1
вычитается.
ЛБ2. Найдите по правилу Лопиталя – Бернулли
1) а)
; б)
; в)
;
2) а)
; б)
; в)
;
3) а)
; б)
; в)
.
Применение правила можно совмещать с переходом к эквивалентным бесконечным малым величинам и с подстановкой чисел.
Пример 8.
,
дифференцируем числитель и знаменатель:
.
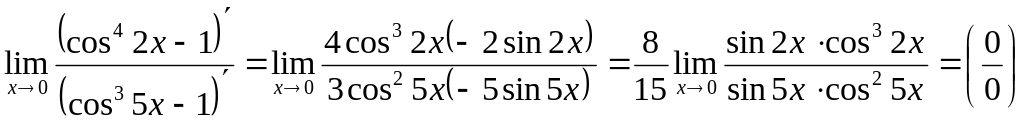Но
,
,
а при
и
,
тогда
.
ЛБ3. Найдите по правилу Лопиталя – Бернулли
1) а)
; б)
; в)
; г)
;
1) а)
; б)
; в)
; г)
.