
Плясов Лабораторный практикум по курсу обсчей физики 2011
.pdf7.В маятнике, используемом в работе, опорные втулки расположены несимметрично относительно точки С. Можно ли расположить эти втулки симметрично относительно этой точки?
8.Измерения каких физических величин в данной лабораторной работе являются прямыми, а каких – косвенными?
9.Как определить, какая из погрешностей прямых измерений вносит максимальный вклад в погрешность окончательного результата?
10.Укажите возможные источники систематических погрешностей в данной работе. Устранимы ли эти источники?
11.Как определить наличие (или отсутствие) в экспериментально полученной величине g (сравнивая ее с табличным значением
этой величины gтабл ) систематической ошибки?
ЛИТЕРАТУРА
Основная
1.Савельев И.В. Курс общей физики. Т. 1. Механика. М: Аст-
рель АСТ, 2003. С. 281–285.
2.Сивухин Д.В. Общий курс физики. Т. 1. Механика. М.: Физ-
матлит, 2006. С. 220–224.
Дополнительная
3. Матвеев А.Н. Механика и теория относительности. М.: ОНИКС 21 век. Мир и Образование, 2003. С. 348–358.
211

Работа 1.15
ОПРЕДЕЛЕНИЕ ПЕРИОДА КОЛЕБАНИЙ И ПРИВЕДЕННОЙ ДЛИНЫ НАКЛОННОГО МАЯТНИКА
Цель: изучение колебаний наклонного маятника; определение периода колебаний и приведенной длины для наклонного маятника.
Оборудование: наклонный маятник; таймер; световой барьер; держатель для светового барьера; соединительные провода; штатив.
ВВЕДЕНИЕ
Под маятником в физике понимают твердое тело, совершающее колебания вокруг неподвижной точки или оси. Принято различать математический и физический маятники.
Математическим маятником называют идеализированную систему, состоящую из невесомой и нерастяжимой нити, на которой подвешена масса, сосредоточенная в одной точке. Достаточно хорошим приближением к математическому маятнику служит небольшой тяжелый шарик, подвешенный на длинной тонкой нити.
Если колеблющееся тело нельзя представить как материальную точку, маятник называется физическим. Таким образом, физический маятник – твердое тело, совершающее колебания вокруг неподвижной оси, жестко связанной с телом.
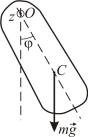
В работе изучаются гармонические колебания наклонного маятника. Гармоническими называют колебания, при которых координата, определяющая положение маятника, например угловое смещение из положения равновесия φ, (рис. 1.15.1) изменяется со временем по закону синуса или косинуса: φ = φ0cos(ω0t + θ0).
Наибольшее отклонение маятника от положения равновесия (максимальное значение величины φ, т.е. φ0) называется амплитудой колебаний. Величина θ = ω0t + θ0, стоящая под знаком косинуса или синуса, называется фазой. Значение фазы колебаний в начальный момент времени θ0 называют начальной фазой.
212
Периодом T называют время одного полного колебания, т.е. время, за которое маятник совершает движение из одного крайнего положения в другое и возвращается обратно
впервоначальное положение.
Вслучае гармонических колебаний возвращающая сила направлена к положению равновесия и является квазиупругой, т.е. сила линейно зависит от смещения φ из этого положения.
При отклонении маятника (см. рис. 1.15.1) от положения равновесия на угол φ сила тяжести создает вращательный момент N,
стремящийся вернуть маятник в положение равновесия. В этом смысле вращательный
момент силы тяжести аналогичен квазиупругой силе, и потому проекция момента N на направление углового ускорения системы отрицательна.
Рассмотрим колебания физического маятника под действием силы тяжести. Выберем положительное направление отсчета угла φ против часовой стрелки (см. рис. 1.15.1). Пусть ось z проходит через точку O и направлена к нам.
Тогда проекция момента силы тяжести на ось z имеет вид
Nz = − mgdsin φ, |
(1.15.1) |
где m – масса маятника; g – ускорение свободного падения; d – расстояние между точкой подвеса O и центром масс маятника С.
В общем случае уравнение движения маятника представляет со-
бой уравнение динамики вращательного движения, которое в про-
екции на ось z имеет вид
Iβz = Nz , |
(1.15.2) |
где βz − угловое ускорение; I – момент инерции тела относительно оси z.
Подставляя (1.15.1) в (1.15.2) получим:
I |
d 2ϕ |
= −mgdsinϕ. |
(1.15.3) |
||
dt |
2 |
||||
|
|
|
|||
Ограничимся рассмотрением малых колебаний, т.е. колебаний, при которых φ << 1, тогда sin φ ≈ φ. В этом случае колебательное
213
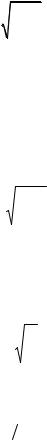
движение маятника будет описываться дифференциальным уравнением гармонических колебаний:
d 2ϕ |
2 |
ϕ = 0 |
|
|
|
|
+ω |
, |
(1.15.4) |
||
dt2 |
|||||
0 |
|
|
|
где введем новое обозначение:
ω = |
mgd |
. |
(1.15.5) |
|
|||
0 |
I |
|
|
|
|
||
Уравнение (1.15.4) имеет решение: |
|
||
φ = φ0 cos(ω0t + θ0), |
(1.15.6) |
||
которое описывает гармонические колебания с амплитудой φ0, начальной фазой θ0, собственной частотой ω0 и периодом T =
= 2π/ω0.
Таким образом, период малых колебаний физического маятника определяется выражением:
T = 2π |
I |
. |
(1.15.7) |
|
|||
|
mgd |
|
|
Математический маятник можно рассматривать как частный случай физического маятника, считая, что вся его масса сосредоточена в одной точке – в центре масс маятника С. В этом случае d = l, I = ml2, где l – длина маятника, и формула (1.15.7) переходит в формулу для периода колебаний математического маятника:
T = 2π |
l |
. |
(1.15.8) |
|
|||
|
g |
|
|
Из сравнения формулы (1.15.7) и (1.15.8) следует, что физический маятник колеблется с тем же периодом, что и математический маятник с длиной
lпр = I md . |
(1.15.9) |
Величина lпр называется приведенной длиной маятника.
При повороте плоскости колебаний на угол β относительно вертикальной плоскости, т.е. для наклонного маятника, формула для периода колебаний имеет вид
214

T = 2π |
lпр |
|
gcosβ . |
(1.15.10) |
Таким образом, можно экспериментально определять с помощью наклонного маятника приведенную длину маятника lпр:
l |
= |
T 2 g cosβ |
. |
(1.15.11) |
|
4π2 |
|||||
пр |
|
|
|
Погрешность приведенной длины, рассчитанной по формуле (1.15.11), определяется выражением:
|
|
lпр |
|
|
g 2 |
2 |
|
T 2 |
|
Δβ |
2 |
|
|||
εlпр |
≡ |
|
= |
|
|
|
+ |
|
|
|
|
+ |
|
. |
(1.15.12) |
l |
g |
|
T |
|
|
||||||||||
|
|
|
|
|
|
|
|
ctgβ |
|
||||||
Здесь |
lпр, g, T, Δβ – абсолютные погрешности измерений соот- |
|
ветствующих величин. |
|
|
Подчеркнем, что в расчетные |
|
|
формулы все значения углов β сле- |
|
|
дует подставлять в радианах. |
|
|
ОПИСАНИЕ УСТАНОВКИ |
|
|
Экспериментальная установка, |
|
|
используемая в работе, представле- |
|
|
на на рис. 1.15.2. Наклонный маят- |
|
|
ник состоит из длинного металли- |
|
|
ческого стержня 1, на котором мо- |
|
|
жет быть закреплен в различных |
|
|
положениях груз 2 (см. рис. 1.15.2). |
|
|
При отклонении стержня от поло- |
Рис. 1.15.2 |
|
жения |
равновесия маятник совер- |
|
шает колебания. Для фиксации прохождения маятника через положение равновесия служит световой барьер 3. Угол отклонения плоскости колебаний от вертикали можно измерять по шкале 4.
Шкала 4, наклонный маятник и световой барьер 3 укреплены на штативе 5. Нивелировочные кольца на треножнике 6 позволяют отрегулировать маятник так, чтобы он был устойчив и чтобы значение угла, считываемое по шкале 4, совпадало с наклоном плоско-
215
сти колебаний по вертикали. Световой барьер при помощи соединительных проводов подключен к источнику питания и к входу 1 таймера 7. На таймере следует выбрать режим «Период колебаний». При этом счетчик фиксирует момент времени, когда стержень колеблющегося наклонного маятника перекрывает луч на световом барьере. Второе перекрывание не берется в учет, а после третьего – измерения прекращаются. Таким образом, измеряется время одного полного колебания маятника (период колебаний).
ПРАВИЛА ТЕХНИКИ БЕЗОПАСНОСТИ
1.После того, как было изменено положение груза на стержне, следует крепко закрутить стопорный винт, чтоб избежать возможного движения груза вдоль стержня при последующих колебаниях маятника.
2.После того, как был изменен угол отклонения плоскости колебаний от вертикали, следует надежно зафиксировать соответствующий винт на штативе с тем, чтобы избежать падения маятника
идержателя светового барьера при последующих качаниях стержня с грузом.
3.Винты следует закручивать крепко, но не перекручивать так, чтобы не отломать их и не сорвать резьбу.
4.Для того чтобы вызвать колебания маятника, не следует слишком сильно отклонять стержень с грузом от положения равновесия.
5.Запрещается разъединять электрические разъемы.
6.Запрещается изменять выставленный на таймере режим работы прибора.
ЗАДАНИЯ
Задание 1. Определение периода колебаний наклонного маятника
1. Поместите подвижный груз 2 вблизи нижнего конца стержня маятника 1. Измерьте геометрическую длину маятника L1 (рас-
стояние между точкой поворота и центром тяжести груза) и запишите ее в заранее подготовленную табл. 1.15.1.
216

2. Установите стержень маятника под углом β = 0° к вертикали. Отклоните маятник на малый угол и измерьте период колебаний Ti для данного значения угла наклона плоскости маятника.
3.Сделайте еще четыре измерения периода колебаний маятника при неизменном положении плоскости колебаний. Результаты занесите в табл. 1.15.1.
4.Поверните плоскость колебаний наклонного маятника в соответствии со значениями угла β, приведенными в табл. 1.15.1. Для каждого значения угла β выполняйте по пять измерений периода колебаний Т малой амплитуды. Результаты измерений занесите в табл. 1.15.1.
Таблица 1.15.1
L1 = |
мм |
|
|
|
|
|
|
||
β, град. |
|
(cos β)-1 |
|
|
Ti, c |
|
|
T , c |
T , c |
|
1 |
2 |
3 |
4 |
5 |
||||
|
|
|
|
|
|||||
0 |
|
|
|
|
|
|
|
|
|
40 |
|
|
|
|
|
|
|
|
|
50 |
|
|
|
|
|
|
|
|
|
60 |
|
|
|
|
|
|
|
|
|
70 |
|
|
|
|
|
|
|
|
|
80 |
|
|
|
|
|
|
|
|
|
L2 = |
мм |
|
|
|
|
|
|
|
|
β, град. |
|
(cos β)-1 |
|
|
Ti, c |
|
|
T , c |
T , c |
|
1 |
2 |
3 |
4 |
5 |
||||
|
|
|
|
|
|||||
0 |
|
|
|
|
|
|
|
|
|
40 |
|
|
|
|
|
|
|
|
|
50 |
|
|
|
|
|
|
|
|
|
60 |
|
|
|
|
|
|
|
|
|
70 |
|
|
|
|
|
|
|
|
|
80 |
|
|
|
|
|
|
|
|
|
5. Измените геометрическую длину маятника и запишите в табл. 1.15.1 ее новое значение L2 (рекомендуется выбирать
L2 =1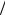 2 L1 ).
2 L1 ).
6. Проведите для новой длины маятника еще одну серию измерений и согласно пп. 2–4. Результаты заносите в табл. 1.15.1.
217
Задание 2. Определение приведенной длины маятника для заданного ускорения свободного падения
1.Зафиксируйте плоскость колебаний маятника в вертикальном положении (β = 0°).
2.Поместите подвижный груз на расстоянии L =1 4 L1 от оси
4 L1 от оси
вращения. Запишите это расстояние в заранее подготовленную табл. 1.15.2.
3. Выполните пять измерений периода Ti колебаний малой ам-
плитуды при неизменной геометрической длине маятника L. Результаты измерений заносите в табл. 1.15.2.
4. Поместите подвижный груз на расстоянии L = 3 4 L1 от оси
4 L1 от оси
вращения. Запишите это расстояние в табл. 1.15.2 и проведите для него измерения согласно п. 3.
Таблица 1.15.2
L, мм |
|
|
Ti , c |
|
|
T , c |
T , с |
lпр, |
lпр, |
|
1 |
2 |
3 |
4 |
5 |
|
|
мм |
мм |
1/4L1 |
|
|
|
|
|
|
|
|
|
1/2L1 |
|
|
|
|
|
|
|
|
|
3/4L1 |
|
|
|
|
|
|
|
|
|
L1 |
|
|
|
|
|
|
|
|
|
ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ
Задание 1
1. Рассчитайте для каждого значения угла β средние значения периода колебаний. Погрешностью измерения времени T следует считать приборную погрешность, если показания отличаются последней значащей цифрой. В том случае, когда в измерениях времени присутствует случайный разброс, значение погрешности T
нужно определить методом Корнфельда. Результаты расчета  T
T  и
и
T занесите в табл. 1.15.1.
2. По данным табл. 1.15.1 постройте в одних осях графики за-
висимости квадрата периода колебаний маятника T 2 от величины (1/cos β) для обоих значений длин маятника.
218
3.По каждому из графиков определите угловой коэффициент k наклона графика к оси абсцисс. Для определения k используйте метод парных точек.
4.Рассчитайте отношение k1/k2 и сравните его со значением величины L1/L2.
Задание 2
1. |
Рассчитайте среднее значение периода колебаний T = T , а |
||
также его абсолютную T погрешность. |
Результаты занесите в |
||
табл. 1.15.2. |
|
|
|
2. |
Занесите в табл. 1.15.2 значения Ti , |
T = T |
и T , получен- |
ные в задании 1 для β = 0°в случаях, когда L = L1 |
и L = L2 =1 2 L1 . |
||
3. Для каждого значения L по формулам (1.15.11) и (1.15.12) рассчитайте значения эффективной (приведенной) длины маятника lпр и их погрешности.
4.Сравните представленные в табл. 1.15.2 соответствующие значения величин l пр и L .
5.По данным из табл. 1.15.2 постройте график зависимости приведенной длины маятника lпр от величины L.
ПРЕДСТАВЛЕНИЕ РЕЗУЛЬТАТОВ РАБОТЫ
В заключении к работе по результатам первого задания предста-
вить график зависимости квадрата периода колебаний маятника T 2 от величины (1/cos β) для обоих значений длин маятника. Сделать вывод о характере полученных зависимостей и о значении величины приведенной длины маятника в данном эксперименте. Сравнить отношение угловых коэффициентов графиков k1/k2 и величины L1/L2.
По результатам задания 2 представить график зависимости приведенной длины маятника lпр от величины L. Обсудить характер полученной зависимости. Сделать вывод о справедливости использования формул для математического маятника в случае различных величин геометрической длины маятника L .
219
Табличные значения
Ускорение свободного падения |
g = 9.8156 м/с2 |
КОНТРОЛЬНЫЕ ВОПРОСЫ
1.Какие измерения в работе являются прямыми, а какие – косвенными?
2.Как в работе следует определять погрешность измерения времени?
3.От чего в работе будет зависеть погрешность в определении приведенной длины маятника?
4.Дайте определение гармонических колебаний.
5.Что называется периодом, амплитудой гармонического колебания?
6.Что такое математический маятник?
7.Что такое физический маятник?
8.Что называется приведенной длиной физического маятника?
9.Какова зависимость периода колебаний наклонного маятника от угла отклонения плоскости колебаний от вертикали?
10.Объясните, как изменение геометрической длины маятника влияет на момент инерции маятника, его приведенную длину, период его колебаний.
11.Известно, что на поверхности Луны ускорение свободного
падения gЛ составляет 16,6 % от ускорения свободного падения Земли g. Рассчитайте такой угол β, чтобы маятник в лаборатории колебался с тем же периодом, с каким он колеблется на Луне в вертикальном положении. (Вычисления рекомендуется проводить для случая, когда подвижный груз находится внизу стержня маятника.)
12.Математический маятник с длиной нити l установлен на тележке, скатывающейся без трения вниз по наклонной плоскости, составляющей угол β с горизонтом. Определите период колебаний маятника.
13.Сформулируйте основное уравнение динамики вращательного движения тел с закрепленной осью.
14.Выведите формулу для периодов незатухающих гармонических колебаний физического и математического маятников.
220
