
Плясов Лабораторный практикум по курсу обсчей физики 2011
.pdf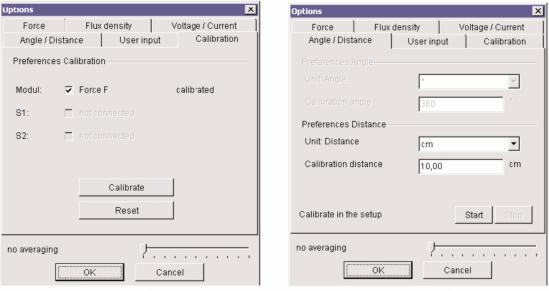
а) |
б) |
Рис. 1.6.6
3. Произвести калибровку датчика движения. Для этого закрепить в установке пружину так, чтобы нить, проходящая через датчик движения, была натянута, но пружина при этом находилась около положения равновесия. Нажать кнопку «Параметры», выбрать в окне программы вкладку «Угол/Расстояние» и установить длину равной 10 см (рис. 1.6.6, б). Для начала калибровки нажать кнопку «Старт», затем медленно, с постоянной скоростью перемещать круглое основание со стойкой вдоль измерительной линейки на расстояние, равное 10 см. Закончить калибровку, нажав на кнопку «Стоп».
ПРАВИЛА ТЕХНИКИ БЕЗОПАСНОСТИ
1.При увеличении или уменьшении нагрузки образца соблюдать осторожность, перемещать круглое основание медленно.
2.Следить, чтобы нить не соскакивала со шкива датчика перемещения.
3.Не пытайтесь растягивать пружины более чем на 30 см! Это может привести к их пластической деформации и невозможности их дальнейшего использования.
4.При замене образца не прилагайте излишних усилий к крючку датчика силы! Это может повредить датчик.
ЗАДАНИЯ
Задание 1. Проверка закона Гука
иопределение коэффициента упругости пружины
1.Снять зависимость удлинения от приложенной силы для первой пружины. Для этого установить круглое основание в начальное положение. Нажать кнопку «Далее» в окне параметров программы. Для начала измерений нажать кнопку «Начать измерения». Медленно, с постоянной скоростью переместить стойку вдоль измери-
тельной линейки на расстояние 20 −30 см. Нажать кнопку «Закончить измерения». Вернуть стойку в начальное положение.
2. На экране появится график зависимости удлинения от приложенной силы. Щелкнуть правой кнопкой мыши по пиктограмме с таблицей в правом верхнем углу графика, или в главном меню программы «Measure» выбрать пункты «Измерение», затем «Таблица данных». На экране появится окно с экспериментальными данными. Занести результаты измерений в заранее подготовленную табл. 1.6.1.
102

Таблица 1.6.1
l , мм
F, Н
3.Снять зависимость удлинения от приложенной силы для второй пружины. Для этого закрепить в установке вторую пружину и повторить действия пп. 1 и 2. Результаты измерений занести в заранее подготовленную таблицу, аналогичную табл. 1.6.1.
Задание 2. Изучение гистерезисной кривой нагрузки
иразгрузки резины
1.Измерить штангенциркулем ширину a0 , толщину b0 и на-
чальную длину l0 резинового жгута. Записать полученные значения
влабораторный журнал.
2.Снять кривые нагрузки и разгрузки образца. Для этого закрепить резиновый жгут в установке. Поместить круглое основание в начальное положение. Нажать кнопку «Далее» в окне параметров программы. Для начала измерений нажать кнопку «Начать измерения». Медленно, с постоянной скоростью переместить стойку
вдоль измерительной линейки на расстояние 20 −30 см. Затем также медленно и плавно вернуть основание в исходное положение. Нажать кнопку «Закончить измерения». Результаты измерений занести в табл. 1.6.2.
Таблица 1.6.2
l , мм
F , Н
ε
σ, Н/м2
ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ
Задание 1
1. По данным таблиц, созданных в задании 1, для обеих пружин на одном листе построить график зависимости силы F от удлине-
103
ния l. Если установка была откалибрована правильно, то графики должны быть почти прямолинейными.
2. Определить коэффициент жесткости каждой пружины. Для этого рассчитать угловые коэффициенты обоих графиков методом парных точек (см. раздел «Введение»). Погрешность коэффициента жесткости оценить методом Корнфельда.
Задание 2
1.Рассчитать относительное удлинение жгута ε и напряжение
σдля каждой экспериментальной точки по формулам:
ε = |
l |
; |
σ = |
F |
, |
||
l |
S |
0 |
|||||
|
|
|
|
||||
|
0 |
|
|
|
|
||
где S0 = a0b0 – начальное поперечное сечение жгута.
2. По данным табл. 1.6.2 построить график зависимости величины относительного удлинения ε от растягивающего напряжения σ для процессов нагрузки и разгрузки
ПРЕДСТАВЛЕНИЕ РЕЗУЛЬТАТОВ РАБОТЫ
В заключении к работе представить графики зависимости приложенной силы от удлинения для двух пружин и график зависимости относительного удлинения от растягивающего напряжения для резинового жгута.
По результатам первого задания сравнить полученные графики с теоретической зависимостью. Привести рассчитанные коэффициенты жесткости пружин. Сравнить их с табличными значениями. Сделать вывод о справедливости закон Гука.
По результатам второго задания сделать вывод о наличии у резины нелинейной зависимости между удлинением и приложенной силой и явления гистерезиса.
Табличные значения |
|
|
|
|
|
Коэффициенты жесткости |
|
|
Первая пружина |
|
k1 = 3 Н/м |
Втораяпружина |
|
k2 = 20 Н/м |
104 |
|
|
КОНТРОЛЬНЫЕ ВОПРОСЫ
1.К какому виду фундаментальных взаимодействий относятся силы упругости?
2.Что такое механическое напряжение, относительное удлинение упругого тела?
3.Сформулировать закон Гука для стержней.
4.Что такое упругая деформация?
5.Что такое предел пропорциональности, предел упругости?
6.В чем состоят и как объясняются свойства высокой эластичности резины?
7.Какое явление называется упругим гистерезисом?
8.В какой области значений относительного удлинения имеет место линейная зависимость растягивающей силы от относительного удлинения в случае резины?
9.Как проявляются свойства усталости у резины?
10.Почему для резины наблюдаются отклонения от закона Гука?
ЛИТЕРАТУРА
Основная
1.Савельев И.В. Курс общей физики. Т. 1. Механика. М.: Аст-
рель АСТ, 2004. С. 69–73.
2.Сивухин Д.В. Общий курс физики. Т. 1. Механика. М.: Физ-
матлит, 2006. С. 404–420.
Дополнительная
3. Фейнман Р., Лейтон Р., Сэндс М. Фейнмановские лекции по физике. Т. 7. Физика сплошных сред. М.: Мир, 1965. С. 188–197.
105

Работа 1.7
МОДУЛЬ УПРУГОСТИ
Цель: изучение упругих деформаций твердых тел; определение модуля Юнга металла.
Оборудование: установка для изучения прогиба пластин; стрелочный микрометр; набор разновесов; набор пластин разного сечения; штангенциркуль; рулетка.
ВВЕДЕНИЕ
Все реальные тела деформируемы, т.е. под действием приложенных сил они меняют форму или объем. Эти изменения называ-
ются деформациями.
В случае твердых тел различают два предельных случая: упругие деформации и пластические деформации. Упругими называются деформации, исчезающие после прекращения воздействия приложенных сил. Пластическими, или остаточными, называют деформации, которые сохраняются в теле, по крайней мере, частично и после прекращения действия внешних приложенных сил. Является деформация упругой или пластической, зависит не только от материала, но и от приложенных сил.
Если сила, отнесенная к единице площади, т.е. напряжение, не превосходит известной величины, называемой пределом упругости, то деформация – упругая, в ином случае она будет пластической. Предел упругости имеет различные значения для разных материалов. Разделение на упругие и пластический деформации условно, и предел упругости не является четко определенной величиной. Строго говоря, все деформации после прекращения воздействия внешних сил исчезают не полностью, т.е. являются пластическими, однако если остаточные деформации малы, то во многих случаях их можно не принимать во внимание. Предельное значение остаточной деформации, при котором ей можно пренебрегать, зависит от каждой конкретной задачи, в некоторых случаях можно пренеб-
106
регать остаточными деформациями, если они составляют 0,1 % от максимальных деформаций, возникающих при нагрузке образца, в иных случаях предел должен быть снижен до 0,01 %, все зависит от рассматриваемой задачи. В лабораторной работе изучаются только упругие деформации.
Упругие свойства тел можно описать при помощи некоторых эмпирических величин, называемых упругими постоянными. Упругие постоянные различны для разных тел и зависят от физического состояния этих тел. Более подробное описание упругих свойств тел с атомистической точки зрения дает теория твердого тела.
Твердые тела разделяются на изотропные и анизотропные. Изотропными называются тела, свойства которых одинаковы по всем направлениям, анизотропными – свойства которых зависят от направления, например кристаллы. Металлы обычно имеют поликристаллическую структуру, т.е. состоят из большого числа мельчайших монокристаллов. Поэтому, хотя каждый кристаллик обладает анизотропией, весь металлический образец, состоящий из множества по-разному ориентированных монокристаллов, в целом можно считать изотропным. При описании деформации металлических образцов, используемых в работе, материал образцов считается изотропным.
В механике при рассмотрении упругих деформаций вводится понятие абсолютно упругих тел, т.е. идеализированных тел, которые могут испытывать только упругие деформации. Для идеально упругих тел существует однозначная зависимость между действующими силами и вызываемыми ими деформациями. Кроме того, для рассмотрения вводится понятие малых деформаций, т.е. упругих деформаций, подчиняющихся закону Гука. Этот приближенный закон гласит, что деформации пропорциональны силам их вызывающим.
Рассмотрим произвольное деформированное тело или среду. Мысленно разделим его на две части: тело 1 и тело 2, граничащие между собой вдоль поверхности АВ (рис. 1.7.1). Так как тело 1 деформировано, то оно действует на тело 2 с некоторой силой. По третьему закону Ньютона тело 2 действует на тело 1 с такой же по модулю, но противоположно направленной силой. Однако для определения возникающих деформаций недостаточно знать суммар-
107

ные силы, действующие в сечении АВ. Надо еще указать, как эти силы распределены по этому сечению.
Рис. 1.7.1
Рассмотрим бесконечно малую площадку dS на поверхности АВ. Пусть dF – сила, с которой на этой площадке тело 2 действует на тело 1. Сила, отнесенная к единице площади, т.е. dF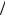 dS , называет-
dS , называет-
ся напряжением, действующим в соответствующей точке на границе АВ тела 1.
Ориентацию площадки dS можно задать, указав направление нормали к ней. Условимся эту нормаль проводить наружу от поверхности тела, на которое действует сила dF . Обозначим через n единичный вектор нормали, а через σn = dF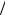 dS – соответствующее
dS – соответствующее
напряжение. Вектор σn можно разложить на составляющую вдоль
нормали n и на составляющую, лежащую в касательной плоскости к площадке dS. Первая составляющая называется нормальным, а
вторая – тангенциальным напряжениями, действующими на пло-
щадке dS.
В общем случае для того, чтобы характеризовать напряжения, возникающие в малой окрестности рассматриваемой точки упругого тела, необходимо выбрать в этой точке три взаимно перпендикулярных площадки и рассмотреть три вектора напряжения. Таким
108
образом, напряжения, возникающие в окрестности этой точки, будут определяться совокупностью девяти величин (по три проекции трех векторов). Совокупность этих девяти величин называется
тензором упругих напряжений.
В изотропном симметричном теле количество величин, определяющих напряжения, сокращается до трех (в этом случае тензор упругих напряжений симметричен и его можно привести к диагональному виду).
Если же рассмотреть тонкий стержень, к основаниям которого приложены перпендикулярные основаниям растягивающие или сжимающие силы, то для определения деформаций достаточно ввести всего лишь одну переменную, называемую нормальным напряжением. Нормальное напряжение определяется как отношение силы, действующей на основание стержня, к площади поперечного сечения стержня σ = F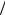 S . Оно положительно в случае растяжения
S . Оно положительно в случае растяжения
и отрицательно в случае сжатия стержня. В случае растяжения стержня положительные напряжения называют натяжениями, а при сжатии стержня вводится понятие давления, которое можно рассматривать как отрицательное напряжение.
Если длина недеформированного стержня равна l0, а после приложения к нему силы F, перпендикулярной его основанию, его длина получает приращение l и становится равной l0+ l, тогда само приращение l называется абсолютным удлинением, а отношение ε = l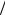 l0 – относительным удлинением стержня. В случае
l0 – относительным удлинением стержня. В случае
растяжения оно положительно, в случае сжатия отрицательно. Опыт показывает, что для не слишком больших упругих
деформаций напряжение σ пропорционально относительному
удлинению: |
|
σ = Eε, |
(1.7.1) |
где E – постоянная, зависящая только от материала стержня и его физического состояния, называемая модулем Юнга вещества.
Формула (1.7.1) выражает закон Гука для деформаций растя-
жения и сжатия стержней. Как уже отмечалось, этот закон приближенный и может не выполняться для больших деформаций.
В настоящей работе исследуется только один вид упругих деформаций – изгиб. Рассмотрим изгиб однородного бруса (балки) произвольного поперечного сечения, линейные размеры которого
109
много меньше длины бруса. Кроме того, будем рассматривать брус, сечение которого одинаково по всей длине.
а |
б |
Рис. 1.7.2
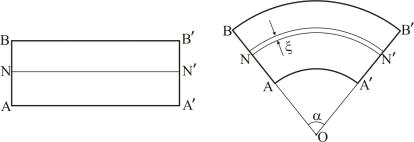
Пусть до деформации брус имел прямоугольную форму. Мысленно вырежем из бруса бесконечно малый элемент AA′BB′ , проведя сечения AB и A′B′, нормальные к его оси. Длину этого элемента обозначим через l0. Ввиду бесконечной малости выделенного элемента можно считать, что в результате изгиба прямые AA' , NN ' , BB ' и все прямые, параллельные им, перейдут в дуги окружности с центрами, лежащими на оси O (рис. 1.7.2), перпендикулярной к плоскости рисунка. Эта ось называется осью изгиба.
Длина средней линии NN ' остается неизменной. Эта линия называется нейтральной линией. Проходящее через нее сечение недеформированного бруса плоскостью, перпендикулярной плоскости рисунка, называется нейтральным сечением. Наружные волокна, т.е. волокна, лежащие выше линии NN ' , при изгибе удлиняются, волокна, лежащие ниже линии NN ' , называемые внутренними волокнами, укорачиваются. Таким образом, все наружные волокна будут растянуты, все внутренние – сжаты.
Пусть R – радиус кривизны нейтральной линии NN ' . Тогда длина недеформированного бруса l0 = Rα , где α – центральный угол, опирающийся на дугу NN ' .
Рассмотрим волокно бруса, находящееся на расстоянии ξ от нейтрального сечения (см. рис. 1.7.2, б). Величина ξ положительна, если волокно находится выше нейтрального сечения, и отрицательна, если оно находится ниже нейтрального сечения.
110
