Заключение

Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный исследовательский ядерный университет (МИФИ)

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Чугунков Методы и средства оценки качества генераторов 2012.pdf

Скачиваний:

Добавлен:

12.11.2022

Размер:

4.26 Mб

Скачать

☆

1 / 51 2 3 4 5 > Следующая >>>

Министерство образования и науки Российской Федерации

НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ ЯДЕРНЫЙ УНИВЕРСИТЕТ «МИФИ»

И.В. ЧУГУНКОВ

МЕТОДЫ И СРЕДСТВА ОЦЕНКИ КАЧЕСТВА ГЕНЕРАТОРОВ ПСЕВДОСЛУЧАЙНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ, ОРИЕНТИРОВАННЫХ НА РЕШЕНИЕ ЗАДАЧ ЗАЩИТЫ ИНФОРМАЦИИ

Рекомендовано УМО «Ядерные физика и технологии» в качестве учебного пособия

для студентов высших учебных заведений

Москва 2012

УДК 621.377.621.12 (075.8) ББК 32.973.202я7 Ч83

Чугунков И.В. Методы и средства оценки качества генераторов псевдо-

случайных последовательностей, ориентированных на решение задач защи-

ты информации: Учебное пособие. М.: НИЯУ МИФИ, 2012. – 236 с.

Излагаются вопросы исследования статистической безопасности генераторов псевдослучайных чисел, предназначенных для решения задач криптографической защиты информации.

Пособие предназначено для студентов вузов и аспирантов, обучающихся по компьютерным специальностям, а также специальностям, связанным с обеспечением безопасности компьютерных технологий.

Рекомендуется использовать при изучении дисциплин «Методы и средства защиты компьютерной информации», «Безопасность информационных систем» для студентов, обучающихся по специальности «Вычислительные машины, комплексы, системы и сети». Может быть полезно разработчикам и пользователям компьютерных систем.

Подготовлено в рамках Программы создания и развития НИЯУ МИФИ.

Рецензент канд. техн. наук В.Г. Грибунин

ISBN 978-5-7262-1690-4 © Национальный исследовательский ядерный университет «МИФИ», 2012

ОГЛАВЛЕНИЕ
ОСНОВНЫЕ ОБОЗНАЧЕНИЯ............................................................	6
ВВЕДЕНИЕ ...........................................................................................	9
ГЛАВА 1. МАТЕМАТИЧЕСКИЕ ПРЕДПОСЫЛКИ......................	10
1.1. Биномиальные коэффициенты ...............................................	10
1.2. Числа Стирлинга......................................................................	12
1.2.1. Числа Стирлинга первого рода.......................................	12
1.2.2. Числа Стирлинга второго рода .......................................	14
1.3. Целочисленные функции........................................................	15
1.4. Дискретное преобразование Фурье........................................	16
1.5. Функция ошибок......................................................................	17
1.6. Функция Лапласа.....................................................................	18
1.7. Функция нормального распределения...................................	20
1.8. Гамма-функция........................................................................	20
1.9. Неполная гамма-функция .......................................................	21
1.9.1. Верхняя неполная гамма-функция..................................	21
1.9.2. Нижняя неполная гамма-функция..................................	22
1.10. P-value .....................................................................................	23
1.11. Критерий χ2.............................................................................	27
1.12. Критерий Колмогорова–Смирнова......................................	32
1.13. Критерий Андерсона–Дарлинга...........................................	35
ГЛАВА 2. СИСТЕМА ОЦЕНКИ СТАТИСТИЧЕСКИХ
СВОЙСТВ «DIEHARD».....................................................................	37
2.1. Проверка дней рождения ........................................................	40
2.2. Проверка пересекающихся перестановок .............................	44
2.3. Проверка рангов матриц .........................................................	46
2.4. Обезьяньи тесты.......................................................................	50
2.5. Подсчет единиц........................................................................	55
2.6. Тест парковки...........................................................................	57
2.7. Тест минимальных расстояний ..............................................	60
2.8. Тест случайных сфер...............................................................	62
2.9. Тест сжатия...............................................................................	65
2.10. Проверка пересекающихся сумм..........................................	68
2.11. Проверка на монотонность...................................................	69
2.12. Тест игры в кости...................................................................	72
2.13. Тест гориллы..........................................................................	75
2.14. Тест НОД................................................................................	78
3

ГЛАВА 3. ПОДБОРКА ТЕСТОВ Д. КНУТА...................................	87
3.1. Проверка равномерности........................................................	87
3.2. Проверка серий........................................................................	90
3.3. Проверка интервалов...............................................................	91
3.4. Покер-тест................................................................................	92
3.5. Тест собирателя купонов ........................................................	94
3.6. Проверка перестановок...........................................................	96
3.7. Проверка на монотонность.....................................................	97
3.8. Тест «максимум-t»...................................................................	99
3.9. Проверка конфликтов............................................................	101
3.10. Проверка дней рождений....................................................	102
3.11. Проверка корреляции..........................................................	102
ГЛАВА 4. РУКОВОДСТВО НИСТ.................................................	106
4.1. Частотный тест.......................................................................	109
4.2. Частотный тест в подпоследовательностях.........................	110
4.3. Проверка на равномерность..................................................	112
4.4. Проверка на равномерность в подпоследовательностях....	114
4.5. Проверка рангов матриц .......................................................	117
4.6. Спектральный тест ................................................................	118
4.7. Проверка непересекающихся шаблонов..............................	120
4.8. Проверка пересекающихся шаблонов..................................	124
4.9. Универсальный статистический тест Маурера...................	128
4.10. Сжатие при помощи алгоритма Лемпела–Зива ................	131
4.11. Проверка линейной сложности ..........................................	133
4.12. Проверка серий....................................................................	137
4.13. Проверка аппроксимированной энтропии.........................	139
4.14. Проверка кумулятивных сумм ...........................................	141
4.15. Проверка случайных отклонений.......................................	143
4.16. Разновидность проверки случайных отклонений.............	147
4.17. Стратегия тестирования и интерпретация результатов ...	150
4.17.1. Выбор тестируемого генератора.................................	151
4.17.2. Генерация последовательностей для тестирования..	151
4.17.3. Исполнение набора статистических тестов...............	152
4.17.4. Анализ прохождения статистических тестов ............	153
4.17.5. Принятие решения о свойствах генератора...............	156
ГЛАВА 5. ДРУГИЕ ТЕСТЫ............................................................	157
5.1. Система CRYPT-X.................................................................	157
5.1.1. Частотный тест...............................................................	157
4

5.1.2. Частотный тест в подпоследовательностях.................	158
5.1.3. Проверка серий...............................................................	162
5.1.4. Проверка на равномерность..........................................	163
5.1.5. Сложность последовательности....................................	167
5.1.6. Линейная сложность......................................................	168
5.1.7. Бинарное ускорение.......................................................	171
5.1.8. Бинарное ускорение в подпоследовательностях.........	172
5.1.9. Точка расхождения.........................................................	176
5.1.10. Точка расхождения в подпоследовательностях ........	178
5.2. Тест «Стопка книг» ...............................................................	180
ГЛАВА 6. ПОВЫШЕНИЕ ЭФФЕКТИВНОСТИ
ОЦЕНОЧНЫХ ТЕСТОВ..................................................................	184
6.1. Проверка категорий...............................................................	184
6.2. Подсчет числа отсутствующих слов....................................	190
ГЛАВА 7. ГРАФИЧЕСКИЕ ТЕСТЫ...............................................	197
7.1. Гистограмма распределения элементов
последовательности......................................................................	198
7.2. Распределение на плоскости.................................................	200
7.3. Проверка серий......................................................................	207
7.4. Проверка на монотонность...................................................	210
7.5. Автокорреляционная функция .............................................	213
7.6. Спектральный тест ................................................................	219
7.7. Профиль линейной сложности.............................................	221
ГЛАВА 8. РАЗРАБОТКА СИСТЕМЫ ОЦЕНКИ КАЧЕСТВА
ГЕНЕРАТОРОВ ПСЕВДОСЛУЧЕЙНЫХ ЧИСЕЛ........................	223
ЗАКЛЮЧЕНИЕ.................................................................................	232
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ.........................	233

ОСНОВНЫЕ ОБОЗНАЧЕНИЯ
Обозначение		Значение				Раздел
Обозначение		Значение				Раздел
f k		Сумма всех	f k , таких,		что
f k		значение k – целое и выполняется
R k		значение k – целое и выполняется
R k		R k
		R k
min f k		Минимальное	значение	из	всех
min f k		f k , таких, что значение k – целое
R k		и выполняется R k
		и выполняется R k
max f k		Максимальное	значение	из	всех
max f k		f k , таких, что значение k – целое
R k		и выполняется R k
		и выполняется R k
n
		Биномиальный коэффициент				1.1
		Биномиальный коэффициент				1.1
i
n		Число Стирлинга первого рода				1.2.1
		Число Стирлинга первого рода				1.2.1
k
n *		Беззнаковое число Стирлинга				1.2.1
		первого рода				1.2.1
k		первого рода
n		Число Стирлинга второго рода				1.2.2
		Число Стирлинга второго рода				1.2.2
k
xn		Убывающий факториальный				1.2
xn		многочлен				1.2
		многочлен
		Возрастающий факториальный				1.2
xn		Возрастающий факториальный
xn		многочлен
		многочлен
x		Функция «пол» – наибольшее целое,				1.3
x		меньшее либо равное x				1.3
		меньшее либо равное x
x		Функция «потолок» – наименьшее				1.3
		целое, большее либо равное x
DFT x		Дискретное преобразование Фурье				1.4

	6

Обозначение

Значение

Раздел

erf x

2 du – функция ошибок

e u

1.5

2 du – дополнительная

erfc x

e u

1.5

функция ошибок

igamc x

Библиотечная

функция

для

вычисления статистики теста,

см.

P-value , 2 obs

P x

Вероятность события x

1.6

ФL x

z 2

– функция Лапласа

1.6

2 0

Г n

1e t dt

– гамма-функция

1.8

Г n, x

1e t dt

– верхняя неполная

1.9.1

гамма-функция

γ n, x

tn 1e t dt

– нижняя неполная

1.9.2

гамма-функция

2 obs

Статистика для критерия 2

1.11

P-value

Величина, используемая для оценки

результатов статистического

1.10

тестирования

Обозначение

Значение

Раздел

erfс

– значение P-value для

P-value X , ,

1.10

нормированной

нормальной

вели-

чины с математическим ожиданием

μ и средним квадратическим откло-

нением σ

erfс

– значение P-value для

P-value

модуля нормированной нормальной

1.10

величины с математическим ожида-

нием μ и средним квадратическим

отклонением σ

2 obs

t 2

2 obs

igamc

–

P-value , 2 obs

1.11

2 Г

P-value

значение

для

статистики

χ2 obs

критерия

2 с числом сте-

пеней свободы, равным

ВВЕДЕНИЕ

Генераторы псевдослучайных последовательностей (ПСП) являются неотъемлемым элементом любой системы защиты. Именно от их свойств зависят надежность и безопасность процессов сбора, обработки, передачи и хранения информации, а также управления объектами. В связи с этим к формируемым последовательностям предъявляются наиболее жесткие требования. В идеале, по своим статистическим свойствам формируемая последовательность должна быть неотличима от истинно случайной.

Настоящая книга посвящена вопросам оценки статистических свойств генераторов ПСП. В первой главе рассматриваются основные понятия теории вероятностей и математической статистики, используемые при построении тестов для ПСП. Главы со второй по пятую посвящены наиболее известным подборкам оценочных тестов. Во второй главе рассматривается одна из самых первых систем для оценки свойств ПСП – «DIEHARD». Третья глава посвящена подборке тестов Д. Кнута – математическим основам, на которых строятся практически все системы оценки качества ПСП. В четвертой главе представлена специализированная система, разработанная Национальным институтом стандартов и технологий США, ориентированная на исследование криптографических генераторов ПСП. Пятая глава посвящена системе CRYPT-X и отечественному тесту «Стопка книг». В шестой главе рассматриваются вопросы повышения эффективности оценочных тестов. Седьмая глава посвящена графическим тестам, использующимся при оценке статистических свойств генераторов ПСП. В восьмой главе рассматриваются вопросы построения эффективной системы оценки качества генераторов ПСП.

ГЛАВА 1. МАТЕМАТИЧЕСКИЕ ПРЕДПОСЫЛКИ

1.1. Биномиальные коэффициенты

Биномиальные коэффициенты [13] суть коэффициенты n ,

i 0,n в разложении бинома Ньютона для целочисленных n:

a b n n n an 1bi , n = 1, 2, … . i 0 i

В комбинаторике биномиальные коэффициенты интерпретируются как число сочетаний из n по i:

i	n
i
Сn	i .

Значения биномиальных коэффициентов (табл. 1.1) определя-

ются следующим образом:
	n n 1 ... n k 1		n!
				для n k;
n		k!	k! n k !
n		k!	k! n k !
		1		для n k;
		1		для n k;
k		0		для n k.
		0		для n k.

Таблица 1.1. Значения некоторых биномиальных коэффициентов

n						k
n	0	1	2	3	4		5	6	7	9	0
	0	1	2	3	4		5	6	7	9	0
0	1	0	0	0	0		0	0	0	0	0
1	1	1	0	0	0		0	0	0	0	0
2	1	2	1	0	0		0	0	0	0	0
3	1	3	3	1	0		0	0	0	0	0
4	1	4	6	4	1		0	0	0	0	0
5	1	5	10	10	5		1	0	0	0	0
6	1	6	15	20	15		6	1	0	0	0
7	1	7	21	35	35		21	7	1	0	0
8	1	8	28	56	70		56	28	8	1	0
9	1	9	36	84	126		126	84	36	9	1
					10

Биномиальным коэффициентам присущи следующие свойства:

n k

n 1

k 1

k n

n n

m k

k m

...

n 2

...

r s

k 0 m

n k

m n

Пример 1.1

a b 3

a2b

ab2

C30 a3 C31a2b C32 ab2 C33b3 .

C3 0! 3 0 ! 1,

C3 1! 3 1 ! 3,

3	2	3!
	C3
		2! 3 2 ! 3 ,
2
3	3	3!
	C3
		3! 3 3 ! 1 .
3

a b 3 a3 3a2b 3ab2 b3 .

1.2.Числа Стирлинга

Вряде математических формул [12] используются произведения факториального типа, называемые факториальными степенями или факториальными многочленами [13]. Существует два типа факториальных многочленов:

убывающие

n 1

xn x x 1 ... x n 1 x i , n 0 ;

i 0

возрастающие

n 1

xn x x 1 ... x n 1 x i , n 0 .

i 0

Коэффициенты, фигурирующие в преобразовании многочленов, представленного факториальными степенями, в многочлены, выраженные через биномиальные коэффициенты, называются числами Стирлинга.

1.2.1. Числа Стирлинга первого рода

Числа Стирлинга первого рода

s n,k nk

используются для перехода от факториальных степеней к обычным

xn x x 1 ... x n 1 n n xk . k 1 k

Значения чисел Стирлинга первого рода определяются следующим образом:


n		1,
n		0,
		0,
k	n 1	n	n 1
		n	1	k
	k 1			k

еслиn k;

если k 0 и n k или k n; вовсех остальных случаях.

В ряде случаев [11] удобнее пользоваться числами беззнаковыми числами Стирлинга первого рода, в дальнейшем изложении они

n *

будут обозначаться как :

n	n	n	1 n k	n	*
xn x x 1 ... x n 1	xk		1 n k		xk .
k 1	k	k 1		k

Для беззнаковых чисел Стирлинга первого рода справедливы следующие равенства:

n 1 *

k 1

n *

n 1

n *

n!,

k 0

* p

n 1

p k

Некоторые числа Стирлинга первого рода приведены в табл. 1.2.

Таблица 1.2. Числа Стирлинга первого рода

	n							k
	n	0	1	2		3		4	5	6	7	8	9
		0	1	2		3		4	5	6	7	8	9
	0	1	0	0		0		0	0	0	0	0	0
	1	0	1	0		0		0	0	0	0	0	0
	2	0	–1	1		0		0	0	0	0	0	0
	3	0	2	–3		1		0	0	0	0	0	0
	4	0	–6	11		–6		1	0	0	0	0	0
	5	0	24	–50		35		–10	1	0	0	0	0
	6	0	–120	274		–225		85	–15	1	0	0	0
	7	0	720	–1764		1624		–735	175	–21	1	0	0
	8	0	–5040	13068		–13132		6769	–1960	322	0	1	0
	9	0	40320	–109584	118124		–67284		22499	–4536	546	–36	1
Пример 1.2				3		3		3
				3		3		3
	x3 x x 1 x 2 x3					x2		x x3 3x2 2x .
				3		2		1

1.2.2. Числа Стирлинга второго рода

Числа Стирлинга второго рода

S n,k n

используются для перехода от факториальных степеней к обычным

xn n kn xk . k 1

Значения чисел Стирлинга первого рода определяются следующим образом:


n				1,
n				0,
				0,
k		n 1			n 1
	k		k			,
			k			k 1

если n k;

если k 0 или k n;

вовсех остальных случаях.

Некоторые числа Стирлинга второго рода приведены в табл. 1.3.

Таблица 1.3. Числа Стирлинга второго рода

		n																	k
		n		0				1		2			3				4				5			6			7				8	9
				0				1		2			3				4				5			6			7				8	9
		0		1				0		0			0				0				0			0			0				0	0
		1		0				1		0			0				0				0			0			0				0	0
		2		0				1		1			0				0				0			0			0				0	0
		3		0				1		3			1				0				0			0			0				0	0
		4		0				1		7			6				1				0			0			0				0	0
		5		0				1		15			25				10				1			10			0				0	0
		6		0				1		31			90				65				15			1			0				0	0
		7		0				1		63		301				350					140			21			1				0	0
		8		0				1		127		966				1701					1050			266			28				1	0
		9		0				1		255		3025				7770					6951			2646			462				36	1
		Для чисел Стирлинга второго рода справедливы равенства
											n			n *					n
																						1,
																						1,
											n			n					n
												n					n				*	n
										n		1		n 1
										n		1		n 1									2 .

Пример 1.3
x	3		3		3		3		2	3		1	x	3			3x	2			1		3		3		3			2	3
x		x				x				x			x				3x		x			x				x					x
			3				2			1													3				2				1
			2				2				3			2		2x 3 x						2	x x x					3
			2				2		x x		3	3x		2								2						3	.
3			x				x		x x			3x																	.
			2				1
1.3. Целочисленные функции
		Функция «пол» (floor)											x		определяется как наибольшее целое,
меньшее либо равное x:
										x max n Z \| n x .
		Функция «потолок» (ceiling)															x			определяется как наименьшее

целое, большое или равное x:

x min n Z | n x .

Целочисленным функциям присущи следующие свойства [11]:

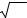
x x x ,

1,	x Z	,
x x	x Z	,
0,	x Z

x x ,x x .

Пример 1.4

1,8 1,1,8 2 ,1,8 2 ,1,8 1.

1.4. Дискретное преобразование Фурье

Дискретное преобразование Фурье [13] (DFT(x)) суть получение функций по гармоникам для нормированной 1 1,0 1 бито-

вой последовательности x = x1,x2,…,xn:

f j xk ei	2 j	k 1 , i 1 .
f j xk ei	n	k 1 , i 1 .
n

k 1

Для упрощения вычислений предлагается использовать сле-

дующую формулу:

2 j

cos

k i sin

k .

Таким образом,

2 j

f j xk cos

k 1

i sin

k 1 .

k 1

Пример 1.5

Вход:

= 1001;

n = 4.

Получение дискретного преобразования Фурье: x = 1, 1, 1, 1,

S = DFT(x),


		4	2									2
S1 f1		xk cos				k	1				i	sin	k 1			2 2i ,
S1 f1		xk cos		4		k	1				i	sin	k 1			2 2i ,
		k 1		4								4
		10		2 2									2 2
S2 f2		xk cos							k	1		i sin			k	1	0 ,
S2 f2		xk cos			4				k	1		i sin	4		k	1	0 ,
		k 1			4								4
		10		2 3									2 3
S3 f3		xk cos						k		1		i sin		k 1			2 2i ,
S3 f3		xk cos			4			k		1		i sin	4	k 1			2 2i ,
		k 1			4								4
		10		2 4									2 4
S4 f4		xk cos							k	1		i sin			k	1	0 .
S4 f4		xk cos		10					k	1		i sin	10		k	1	0 .
M1		k 1		10									10
M1	= modulus (2 – 2i) = 2,
M2	= modulus (0) = 0,
M3	= modulus (2 + 2i) = 2,
M4	= modulus (0) = 0.

1.5. Функция ошибок

Функция ошибок erf (error function) [13] суть функция

erf x	2	x
		e u 2 du .

	0

Интеграл в составе функции является недифференцируемым, то есть его нельзя выразить через элементарные математические функции, однако можно разложить в ряд [17]

erf x

2 x

u 2

1 x5

1 x7

2! 5

3! 7

...

2 1

n 0 n! 2n 1

Существует формула [17] для приближенного вычисления функции ошибки

erf x 1 a1t a2t2 a3t3 a4t4 a5t5 e x2 e x ,

где

t		1	,
	1	px

e x 1,5 10 7 ,

p = 0,3275911, a1 = 0,254829592, a2 = –0,284496736, a3 = 1,421413741, a4 = –1,453152027, a5 = 1,061405429.

Если Х – случайная величина, имеющая нормальное распределение с математическим ожиданием, равным нулю, и стандартным отклонением , то вероятность того, что Х отклонится от среднего не более чем на a, равна

			a
P	X	a erf		.
			2

Пример 1.6

Вход:

a 3 (демонстрация правила «трех сигм» [5, 6], гласящего, что вероятность того, что нормально распределенная случайная величина отклонится от своего математического ожидание на величину, большую, чем утроенное среднее квадратичное отклонение, практически равна нулю)

				3				3
P	X		3 erf				erf		0,9973 .
					2			2


P	X	3 1 P		X		3 1 0,9973 0,0027 .

Через функцию ошибок определяется дополнительная функция ошибок

erfc x 1 erf x	2
		e u 2 du .

	x

1.6. Функция Лапласа

Функция Лапласа [6] суть функция

	1	x	z 2
ФL x		e		dz .
			2

	2 0

Используя значения функции Лапласа (табл. 1.4) можно найти вероятность попадания нормальной случайной величины X с математическим ожиданием и среднеквадратическим отклонением

в интервал , :


P X ФL	ФL	.

Таблица 1.4. Значения функции Лапласа ФL x

x	0	1	2	3	4	5	6	7	8	9
0,0	0,00000	00399	00798	01197	01595	01994	02392	02790	03188	03586
0,1	03983	04380	04776	05172	05567	05962	06356	06749	07142	07535
0,2	07926	08317	08706	09095	09483	09871	10257	10642	11026	11409
0,3	11791	12172	12552	12930	13307	13683	14058	14431	14803	15173
0,4	15542	15910	16276	16640	17003	17364	17724	18082	18439	18793
0,5	19146	19497	19847	20194	20540	20884	21226	21566	21904	22240
0,6	22575	22907	23237	23565	23891	24215	24537	24857	25175	25490
0,7	25804	26115	26424	26730	27035	27337	27637	27935	28230	28524
0,8	28814	29103	29389	29673	29955	30234	30511	30785	31057	31327
0,9	31594	31859	32121	32381	32639	32894	33147	33398	33646	33891
1,0	34134	34375	34614	34850	35083	35314	35543	35769	35993	36214
1,1	36433	36650	36864	37076	37286	37493	37698	37900	38100	38298
1,2	38493	38686	38877	39065	39251	39435	39617	39796	39973	40147
1,3	40320	40490	40658	40824	40988	41149	41309	41466	41621	41774
1,4	41924	42073	42220	42364	42507	42647	42786	42922	43056	43189
1,5	43319	43448	43574	43699	43822	43943	44062	44179	44295	44408
1,6	44520	44630	44738	44845	44950	45053	45154	45254	45352	45449
1,7	45543	45637	45728	45818	45907	45994	46080	46164	46246	46327
1,8	46407	46485	46562	46638	46712	46784	46856	46926	46995	47062
1,9	47128	47193	47257	47320	47381	47441	47500	47558	47615	47670
2,0	47725	47778	47831	47882	47932	47982	48030	48077	48124	48169
2,1	48214	48257	48300	48341	48382	48422	48461	48500	48537	48574
2,2	48610	48645	48679	48713	48745	48778	48809	48840	48870	48899
2,3	48928	48956	48983	49010	49036	49061	49086	49111	49134	49158
2,4	49180	49202	49224	49245	49266	49286	49305	49324	49343	49361
2,5	49379	49396	49413	49430	49446	49461	49477	49492	49506	49520
2,6	49535	49547	49560	49573	49585	49598	49609	49621	49632	49643
2,7	49653	49664	49674	49683	49693	49702	49711	49720	49728	49736
2,8	49744	49752	49760	49767	49774	49781	49788	49795	49801	49807
2,9	49813	49819	49825	49831	49836	49841	49846	49851	49856	49861

3,0	0,49865
3,1	0,49903
3,2	0,49931
3,.3	0,49952
3,4	0,49966
3,5	0,49977
3,6	0,49984
3,7	0,49989
3,8	0,49993
3,9	0,49995
4,0	0,499968
4,5	0,499997
5,0	0,49999997

					19

Пример 1.7

Демонстрация правила «трех сигм» при помощи функции Лапласа.

P 0 3 X	0 3	3 0				3 0		ФL 3 ФL 3
P 0 3 X	0 3	ФL		ФL				ФL 3 ФL 3

2ФL 3 2 0,49865 0,9973.
Значение функции Лапласа можно получить, используя функ-
цию ошибок
			erf		x

					2
		ФL x			2		.
		ФL x		2			.
				2

1.7. Функция нормального распределения

Функция нормального распределения [6] суть функция

Ф x	1	x	z2
		e	2	dz .

	2

Функция нормального распределения может быть вычислена

через функцию Лапласа и функцию ошибок
Ф x	1			x	1			x .
		1	erf			Ф	L
		1	erf			Ф
	2			2	2
	2			2	2

1.8. Гамма-функция

Гамма-функция [1, 17] суть функция

Г z t z 1e t dt , Re z > 0.

Далее рассмотрение функции будет производиться применительно к целым действительным аргументам функции n:

Г n tn 1e t dt.

Основные равенства следующие:

Г1 e t dt 1,

				1	,
		Г		2	,
				2
	1		1 3 5... 2n 1				1
Г n						Г		,
Г n	2				2n	Г	2	,
	2				2n		2

Г n 1 n Г n ... n!Г1 n!.

1.9. Неполная гамма-функция

Под неполной гаммой функцией понимается гамма-функция с переменным пределом интегрирования. В связи с этим различают две неполные гамма-функции: верхнюю (фиксирован верхний передел) и нижнюю (фиксирован нижний предел).

1.9.1. Верхняя неполная гамма-функция

Верхняя неполная гамма-функция суть функция

Г n, x t n 1e t dt .

В частном случае (n = 0) верхняя неполная гамма-функция превращается в обычную гамма-функцию

Г n,0 tn 1e t dt Г n .

Вычисление верхней неполной гамма-функции [2] возможно либо при помощи рекуррентной формулы

Г n 1, x n Г n, x xne x ,

либо при разложении в ряд	1	x		,
Г n, x Г n	1	x		,
	i		n i
i 0	i! n i

либо при помощи разложения Лежандра (Legendre) в бесконечную дробь Гаусса (Gauss)

Г n, x			e x xn
Г n, x	x			1 n
				1 n
		1		1
				1
			x	2		n
				2		n
				1			2
							2
					x		3 n
							3 n
							1
							1

Для верхней неполной гамма-функции также справедливы следующие равенства:

		Г 1, x e x ,
1		, x		erfc	x ,
Г	2

1		, x	2	erfc x .
Г	2

1.9.2. Нижняя неполная гамма-функция

Нижняя неполная гамма-функция суть функция

γ n, x tn 1e t dt .

Нижняя неполная гамма-функция связана с верхней следующим равенством:

γ n, x Г n, x Г n .

Вычисление нижней неполной гамма-функции [2] возможно либо при помощи рекуррентной формулы

n 1, x n Г n, x xne x ,

либо при разложении в ряд

n, x 1 i xn i ,

i 0 i! n i

либо при помощи разложения Лежандра в бесконечную дробь Гаусса

n, x				e x xn
n, x					nx
	n				nx
	n	n 1			n
					n
			n 2		n 1 x
			n 2	n 3		2x
						2x
					n 4	n 2 x

n 5 3x

n 6

Для нижней неполной гамма-функции также справедливы следующие равенства:

		1, x 1 e x ,
1		, x		erf	x ,
	2

1		, x	2	erf	x .
	2

В ряде случаев [16] используют модифицированную нижнюю неполную гамма-функцию

x n x

γ* n, x Г n 0 t n 1e t dt .

1.10. P-value

P-value суть величина, используемая для оценки результатов статистического тестирования [16]. Далее в книге под статистическим тестированием будет пониматься исследование свойств формируемых генераторами последовательностей.

Статистический тест формулируется для проверки определенной нулевой гипотезы H0 о том, что проверяемая последовательность является случайной. С этой нулевой гипотезой связана альтернативная гипотеза На о том, что последовательность не случайна. Для каждого применяемого теста получают заключение о принятии или отклонении нулевой гипотезы, основываясь на сформированной исследуемым генератором последовательности.

Для каждого теста должна быть выбрана подходящая статистика случайности для принятия или отклонения нулевой гипотезы. Согласно предположению о случайности, такая статистика имеет рас-

пределение возможных значений. Теоретическое эталонное распределение данной статистики для нулевой гипотезы определяется математическими методами. Из этого эталонного распределения определяется критическое значение. Во время проведения теста вычисляется значение тестовой статистики. Такое значение сравнивается с критическим. Если значение тестовой статистики превышает критическое значение, нулевая гипотеза для случайности отклоняется. В противном случае, нулевая гипотеза принимается.

Проверка статистических гипотез работает, потому что эталонное распределение и критическое значение зависят и генерируются согласно предварительному предположению о случайности. Если предположение о случайности последовательности истинно, то результирующее значение тестовой статистики для нее будет иметь очень низкую вероятность превышения критического значения

(например, 0,01 %).

С другой стороны, если расчетное значение тестовой статистики превышает критическое значение (то есть происходит событие с низкой вероятностью), то с точки зрения проверки статистической гипотезы, событие с низкой вероятностью не может встретиться естественно. Поэтому когда расчетное значение тестовой статистики превышает критическое значение, делается заключение, что первоначальное предположение о случайности является подозрительно или ошибочно. В этом случае делается заключение об отклонении Н0 (случайность) и принятии На (неслучайность).

Проверка статистической гипотезы – процедура генерации заключения, которая имеет два возможных результата: или принять Н0 (данные случайны), или принять На (данные неслучайны). Табл. 1.5 связывает истинное (неизвестное) состояние данных с заключением, полученным процедурой проверки.

Если данные на самом деле случайны, то заключение об отклонении нулевой гипотезы (то есть данные неслучайны) будет приниматься крайне редко. Это заключение называется ошибкой первого рода. Если данные неслучайны, то заключение о принятии нулевой гипотезы (то есть, что данные случайны) называется ошибкой второго рода. Заключения о принятии Н0, когда данные действительно случайны, и отклонении Н0, когда данные неслучайны, являются правильными.

Таблица 1.5. Принятие заключений по результатам проведения статистических испытаний

Ситуация	Заключение
	Принять Н0	Принять На

Данные случайны	Нет ошибки	Ошибка 1-го рода
(Н0 истинна)

Данные неслучайны	Ошибка 2-го рода	Нет ошибки
(На истинна)

Вероятность ошибки 1-го рода называется уровнем значимости теста. Эта вероятность может быть установлена до испытания и обозначается как . Для теста суть вероятность того, что тест укажет на неслучайность последовательности, тогда как на самом деле она случайна. То есть на то, что последовательность имеет неслучайные свойства, даже если ее произвел хороший генератор.

Вероятность ошибки 2-го рода обозначается как . Для теста есть вероятность того, что тест укажет на случайность последовательности, тогда как это не так; то есть плохой генератор произвел последовательность, которая, как кажется, имеет случайные свойства. В отличие от , не является фиксированным значением, может принимать множество различных значений, потому что существует бесконечное число ситуаций, когда поток данных может

быть неслучаен, и каждая из них выдает различные . Вычисление ошибки 2-го рода является более сложным из-за множества возможных типов неслучайности.

Одна из основных целей статистических тестов – минимизация вероятности ошибки 2-го рода, иначе говоря, минимизация вероятности принятия последовательности, произведенной плохим генератором, за последовательность, произведенную хорошим генера-

тором. Вероятности и связаны друг с другом и с длиной n проверяемой последовательности: если два из этих значений определены, третье определяется автоматически. На практике обычно выбирают размер n и значение для (вероятности ошибки 1-го рода). Тогда критическая точка для данной статистики выбирается так,

чтобы получить наименьшее значение (вероятность ошибки 2-го рода).

Каждый тест основан на вычислении значения тестовой статистики, которое является функцией данных. Если значение тестовой

статистики – S , а t – критическое значение, то вероятность ошибки 1-го рода и 2-го рода есть соответственно

P(S > t || Н0 истинна) = P(отклонить Н0 | Н0 истинна),

P(S t || Н0 ложна) = P(принять Н0 | Н0 ложна). Тестовая статистика использует вычисление значение P-value,

которое констатирует силу доказательства против нулевой гипотезы, иначе говоря, P-value – вероятность того, что совершенный генератор случайных чисел произвел бы последовательность менее случайную, чем исследуемая, для типа неслучайности, проверяемого тестом. Если P-value для теста равно 1, то последовательность абсолютно случайна. P-value, равное 0, указывает, что последовательность абсолютно неслучайна. Для теста следует выбрать уро-

вень значимости . Если значение P-value больше или равно , то принимается нулевая гипотеза, т.е. последовательность кажется

случайной. Если значение P-value меньше , то нулевая гипотеза отклоняется, т.е. последовательность кажется неслучайной. Пара-

метр обозначает вероятность ошибки 1-го рода. Как правило, выбирается в интервале [0,001, 0,01].

Значение , равное 0,001, говорит о том, что из 1000 случайных последовательностей не прошла бы тест лишь одна.

При P-value 0,001 последовательность рассматривается как случайная с доверительностью 99,9 %. При P-value < 0,001 последовательность рассматривается как неслучайная

с доверительностью 99,9 %.

Значение , равное 0,01, говорит о том, что из 100 случайных последовательностей не прошла бы тест лишь одна. При P-

value 0,01 последовательность рассматривается как случайная с доверительностью 99 %. При P-value < 0,01 последовательность рассматривается как неслучайная с доверительностью 99 %.

Найдем значение P-value для нормированной нормальной величины [5]:

z X ,

где X – нормальная величина с математическим ожиданием μ и средним квадратическим отклонением σ.

Согласно определению, P-value характеризует силу доказательства против нулевой гипотезы, следовательно, для нормированной нормальной величины

																					z
								1						1					1	erf
																				erf	2

P-value z 1 Ф z						1				Ф	L	z			Ф	L	z
P-value z 1 Ф z						1				Ф		z			Ф		z
														2					2	2
								2						2					2	2
		z				z
1	erf		erfc
1	erf	2	erfc			2
		2				2			.
	2			2					.
	2			2
Подставляя z					X		, получаем
Подставляя z							, получаем

														X
				P-value X , ,									erfс					.
													erfс		2
															2
															2

Как правило, нормированные нормальные величины применяются при аппроксимации с нормальным законом распределения. В этом случае следует рассчитывать значение P-value применительно

к z :

P-value

2 1 Ф z 2

P-value z

erfс

Примечание: P-value z

можно вычислить при помощи специ-

альных онлайн-калькуляторов (например, z-score-calculator, распо-

ложенного по адресу http://www.zscorecalculator.com/index.php).

1.11. Критерий χ2

Пусть результаты испытаний таковы, что их можно разделить на k категорий. Проводится n независимых испытаний, где n – достаточно большое число. Обозначим через ps вероятность того, что результат испытания попадет в s-ю категорию, а через Ys число испытаний, которые реально попали в s-ю категорию.

Cформируем статистику

k	Y	np	s	2
χ2 obs	s		s		.
χ2 obs		nps			.
s 1		nps

Для оценки полученного результата используются таблицы распределения 2 [12, 17]. В строках табл. 1.6 расположены степени свободы , а в столбцах – P-value.

Таким образом, зная значение х можно определить соответствующее ему значение P-value. Число степеней свободы принимается равным

k 1 .

Число степеней свободы меньше числа категорий на единицу,

так как Ys , s			1,k	не являются полностью независимыми. Это свя-
зано с тем, что, поскольку					k
					k
					Yi n ,
					i 1
то, зная Y1,Y2 ,...,Yk 1 , можно вычислить значение Yk :
							k 1
					Yk n Yi .
							i 1
	Таблица 1.6. Некоторые значения 2-распределения
ν							P-value

		0,99		0,95	0,75		0,50	0,25	0,05	0,01
		0,99		0,95	0,75		0,50	0,25	0,05	0,01
1		0,00016		0,00393	0,1015		0,4549	1,323	3,841	6,635

2		0,02010		0,1026	0,5754		1,386	2,773	5,991	9,210
3		0,1148		0,3518	1,213		2,366	4,108	7,815	11,34

4		0,2971		0,7107	1,923		3,357	5,385	9,488	13,28

5		0,5543		1,1455	2,675		4,351	6,626	11,07	15,09
6		0,8721		1,635	3,455		5,348	7,841	12,59	16,81

7		1,239		2,617	4,255		6,346	9,037	14,07	18,48
8		1,646		2,733	5,071		7,344	10,22	15,51	20,09

9		2,088		3,325	5,899		8,343	11,39	16,92	21,67

10		2,558		3,940	6,737		9,342	12,55	18,31	23,21
20		8,260		10,85	15,45		19,34	23,83	31,41	37,57

30		14,95		18,49	24,48		29,34	34,80	43,77	50,89
						28

Пример 1.8

Уровень значимости теста α = 0,01. В результате вычислений для числа степеней свободы ν = 6 получено две статистики:

χ2 obs 1 7,841 и 2 obs 2 21,365 . Определить, пройдены ли

тесты.

Решение:

Для первой статистики значение 2 obs 1 7,841 для ν = 6 соот-

ветствует P-value1 = 0,25, что больше, чем α = 0,01, следовательно, тест пройден.

Для второй статистики значение 2 obs 2 21,365 для ν = 6 пре-

вышает все значения в 6-й строке, что свидетельствует о том, что P-value2 < 0,01. Таким образом, P-value2 < α, тест не пройден.

Табл. 1.6 предоставляет только некоторые значения, при оценке же результатов теста необходимо иметь конкретное значение, соответствующее заданным числу степеней свободы и статистике теста. Для расчета значения P-value для критерия χ2 можно использовать формулу [17]


			1e		t
	t 2				2	dt
P-value	2 obs						.


22
		Г		2

Вычисление данного выражения реализовано во многих языках программирования и библиотеках к ним. Например, в языке С зна-

чение P-value для статистики 2 obs с ν степенями свободы может

быть вычислено при помощи igamc:				obs
		,	2		,
P-value , 2 obs igamc		,			,
	2			2
	2			2

в библиотеке ESBPCSStatistics для Delphi это делается при помощи функции IncompleteGamma:

		,	2	obs
P-value , 2 obs IncompleteGamma		,		obs	.
	2			2
	2			2

Существуют также специализированные программы, вычис-

ляющие значения P-value для заданного распределения (например, Statistics Calculators, расположенный по адресу http://www.danielsoper.com/statcalc/).

При ручном вычислении значения P-value можно использовать тот факт, что числитель формулы представляет собой верхнюю неполную гамма-функцию. Интегрируя ее по частям и раскладывая полученный результат в ряд, можно получить следующее выраже-

ние [17]:

						t				1e t dt						2 obs i
				1		t		t 2
			t 2	1		2 dt		t 2
			t 2	e		2 dt	2	obs					1	2
	2							obs				2	1		obs	2
	2	obs						2				2				2
P-value								2				e			2
P-value												e			2	i!
		2						22				i 0				i!
		2	2 Г		2			22	Г		2
					2						2

для четных ν.

Пример 1.9

В результате 100 бросков при игре в кости двумя кубиками со значениями костяшек от 1 до 3 были получены следующие результаты:

сумма, равная 2, была выброшена 10 раз;

сумма, равная 3, была выброшена 20 раз;

сумма, равная 4, была выброшена 40 раз;

сумма, равная 5, была выброшена 20 раз;

сумма, равная 6, была выброшена 10 раз.

Применить критерий χ2 для данной совокупности бросков.

Решение: n 100 ;

число категорий k 5 (2, 3, 4, 5, 6);

число степеней свободы k 1 5 1 4.

1-я категория (число исходов, в которых была выброшена сумма 2):

Y1 10 ;

2-я категория (число исходов, в которых была выброшена сумма 3):

Y2 20 ;

3-я категория (число исходов, в которых была выброшена сумма 4):

Y3 40 ;

4-я категория (число исходов, в которых была выброшена сумма 5):

Y4 20 ;

5-я категория (число исходов, в которых была выброшена сумма 6):

Y5 10 .

Соответствующие вероятности равны:

p	1	1	1	(2: 1 на первом кубике и 1 на втором кубике);
1	3	3	9

p2	1	1	1	1		2	(3: 1 на первом кубике и 2 на втором кубике,
				3
	3	3	3		9
или 2 на первом кубике и 1 на втором кубике);
p	1	1	1 1		1		1	3 1 (4: 1 на первом кубике и 3 на втором
3	3	3	3	3	3		3	9	3

кубике, или 2 на первом кубике и 2 на втором кубике, или 3 на первом кубике и 1 на втором кубике);

p4	1	1	1	1	2	(5: 2 на первом кубике и 3 на втором кубике,
p4	3	3	3	1	9	(5: 2 на первом кубике и 3 на втором кубике,
	3	3	3	3	9
или 3 на первом кубике и 2 на втором кубике);
p5	1	1	1	(6: 3 на первом кубике и 3 на втором кубике).
	3	3	9
Вычисляем статистику:

														1 2										2	2
		5					2		10 100								20 100
		5		Ys		nps								9										9
χ2 obs				Ys		nps								9										9
χ2 obs													1										2
		s 1				nps				100			1						100				2
		s 1				nps							9										9
													9										9
		100			1 2			100			2	2				100				1	2
	40						20								10					9
	40						20				9				10
					3						9												2.
		100 1						100		2						100		1					2.
										2								1
																		9
		3						9										9
Вычисляем соответствующее значение P-value:
			2													4				2
P-value ,					obs P-value 4, 2 igamс													,				0,7358 .
P-value ,					obs P-value 4, 2 igamс													,		2		0,7358 .
																2				2
													31

1.12. Критерий Колмогорова–Смирнова

Критерий χ2 может применяться в том случае, когда результаты испытаний могут быть отнесены к конечному числу категорий. Однако имеют место случаи, когда результаты испытаний могут принимать бесконечное множество значений (например, был проведен ряд испытаний, результатом каждого из которых явилось значение P-value, которое, как было показано ранее, может принимать бесконечное множество значений в интервале от 0 до 1). Для оценки таких результатов применяется критерий Колмогорова– Смирнова [5, 6, 12, 30]. Суть его в следующем. Пусть в результате

n испытаний были получены значения Xi , i 1,n . Построим эмпирическую функцию распределения

Fn x	Число X1 X 2	X n ,таких,..., что, они , x	.
		n

Критерий Колмогорова–Смирнова определяет, насколько эмпирическая функция распределения Fn x отличается от функции

распределения F x [5, 6], определяющей вероятность того, что

случайная величина X примет значение, меньше либо равно x для заданного распределения. Для этого вычисляются две статистики:

Кn n max Fn x F x ,

К	n max	F x F x .
n	x	n
	x

Для оценки полученных статистик используются таблицы распределения Кn и Кn [12]. В строках табл. 1.7 расположены значе-

ния n, а в столбцах – P-value. Таким образом, зная значения Кn и

Кn можно определить соответствующие им значения P-value.

Применим критерий Колмогорова–Смирнова для оценки результатов испытаний, использовавших критерий χ2. Пусть проведено n испытаний, в результате которых были получены статистики

2 obs i и соответствующие им значения P-valuei, i 1,n . В этом

случае, F 2 obs i есть не что иное, как значение P-valuei для i-го

испытания. Для того чтобы избавиться от необходимости нахождения максимума по всем x от до , воспользуемся процедурой, предложенной в [12]. Суть ее в следующем.

Таблица 1.7. Некоторые значения распределения Кn								и Кn
n				P-value
n	0,99	0,95	0,75		0,50	0,25	0,05	0,01
	0,99	0,95	0,75		0,50	0,25	0,05	0,01
1	0,01000	0,05000	0,2500		0,5000	0,7500	0,9500	0,9900
2	0,01400	0,06749	0,2929		0,5176	0,7071	1,0980	1,2728
3	0,01699	0,07919	0,3112		0,5147	0,7539	1,1017	1,3589
4	0,01943	0,08789	0,3202		0,5110	0,7642	1,1304	1,3777
5	0,02152	0,09471	0,3249		0,5245	0,7674	1,1392	1,4024
6	0,02336	0,1002	0,3272		0,5319	0,7703	1,1463	1,4144
7	0,02501	0,1048	0,3280		0,5364	0,7755	1,1537	1,4246
8	0,02650	0,1086	0,3280		0,5392	0,7797	1,1586	1,4327
9	0,02786	0,1119	0,3274		0,5411	0,7825	1,1624	1,4388
10	0,02912	0,1147	0,3297		0,5426	0,7845	1,1658	1,4440
20	0,03807	0,1298	0,3461		0,5547	0,7975	1,1839	1,4698
30	0,04354	0,1351	0,3509		0,5605	0,8036	1,1916	1,4801

Полученные значения P-valuei, i 1,n , располагаются в порядке

возрастания. Статистики для критерия Колмогорова–Смирнова вычисляются по следующим формулам:

			i
К		n max		P-value		,
К		n max		P-value		,
	n	1 i n n			i
					i 1
Кn		n max P-valuei				.
Кn		n max P-valuei			n	.
		1 i n			n

Критерий Колмогорова–Смирнова эффективен при исследовании последовательностей большой длины, которые не могут сразу быть обработаны заданным статистическим тестом. В этом случае можно разделить последовательность на отдельные подпоследовательности, получить статистики тестов для каждой из них и оценить полученные результаты при помощи критерия Колмогорова– Смирнова.

Пример 1.10

В результате n = 5 испытаний при помощи критерия χ2 были получены следующие значения:

P-value1 = 0,55;

P-value2 = 0,40;

P-value3 = 0,34;

P-value4 = 0,51;

P-value5 = 0,10.

Оценить полученные результаты при помощи критерия Колмо- горова–Смирнова.

Решение:

Расположим полученные значения P-valuei, i 1,5 , в порядке воз-

растания. Получаем: 0,10; 0,34; 0,40; 0,51; 0,55.

Вычислим статистики критерия Колмогорова–Смирнова:

			1				2		3				4				5
К5		5 max		0,1;				0,34;			0,4;			0,51;					0,55
К5		5 max	5	0,1;			5	0,34;	5		0,4;		5	0,51;			5		0,55
			5				5		5				5				5
	5 max 0,1; 0,06; 0,24; 0,29; 0,45												5 0,45 1.
P-value K5 0,11 .
					1	1				2 1					3	1				4 1
К5		5 max	0,1					; 0,34				; 0,40						; 0,51				;
К5		5 max	0,1			5		; 0,34			5	; 0,40				5		; 0,51			5	;
						5					5					5					5
0,55		5 1		5 max 0,1; 0,14; 0; 0,09; 0,25															5 0,14 0,31.
0,55				5 max 0,1; 0,14; 0; 0,09; 0,25															5 0,14 0,31.
		5

P-value K5 0,78 .

Использование критерия Колмогорова–Смирнова в чистом виде связано с двумя проблемами. Первая из них заключается в трактовке результатов – ведь критерий возвращает две статистики, а они, как видно из примера, могут существенно различаться. Вторая проблема связана со сложностью вычисления значения P-value. В [11] приведена формула для вычисления

		t			t
P-value P K	n		P K	n
P-value P K			P K

		n			n

t		n	n
				k t k t n k n k 1	,
	n
n
		k t 1	k

однако данная формула не позволяет рассчитывать все значения P- value ввиду ограниченности диапазона значений t, поскольку t присутствует в пределах суммирования. Еще одна формула [11]

			2x2	2		1	1
P-value P Kn	x P Kn	x e	1		x		O
P-value P Kn	x P Kn	x e	1		x		O
				3		n	n
				3		n	n

обеспечивает точность вычислений лишь при больших значениях n.

В связи с этим в математической статистике вместо критерия Колмогорова–Смирнова часто применяется критерий Андерсона– Дарлинга (Anderson–Darling) [28].

1.13. Критерий Андерсона–Дарлинга

Пусть в результате n испытаний были получены тестовые статистики Xi , i 1,n . Расположим их в порядке возрастания:

X1 X 2 ... X n .

Вычислим тестовую статистику

где

A2 n S ,

2k 1 ln F Xk ln 1 F Yn 1 k .

k 1

В случае, когда результатом тестов являются P-valuei,

, в

1,n

порядке возрастания располагаются значения последних:

P-value1 P-value2 ...P-valuen

и тестовая статистика принимает вид

A2 n n

2k 1

ln P-value ln 1 P-value

n 1 k

k 1

В [28] приведена формула для расчета P-value для значения А2:

A2 ;

1,2337

0,04958 A

1 A

1,325 A2

P-value

A2 2;

0,6621361 e 1,091638 A2

0,95095 e 2,005138 A2 ,

2 A2 4;

0,4938691 e

1,050321 A2

0,5946336 e

1,527198 A

, A

где α – уровень значимости теста.

Пример 1.11

В результате n = 5 испытаний при помощи критерия χ2 были получены следующие значения:

P-value1 = 0,55;

P-value2 = 0,40;

P-value3 = 0,34;

P-value4 = 0,51;

P-value5 = 0,10.

Оценить полученные результаты при помощи критерия Андер- сона–Дарлинга.

Решение:

Расположим полученные значения P-valuei, i 1,5 , в порядке воз-

растания. Получаем

0,10; 0,34; 0,40; 0,51; 0,55.

Вычислим A2:

A2 n n 2kn 1 ln P-valuek ln 1 P-valuen 1 k .

k 1

A2 5 2 15 1 ln 0,1 ln 1 0,55 2 25 1 ln 0,34 ln 1 0,51

2 35 1 ln 0,4 ln 1 0,4 2 45 1 ln 0,51 ln 1 0,34

2 55 1 ln 0,55 ln 1 0,10 0,91.

Вычислим значение P-value:

		1,2337	0,91		2
	2e		0,91	0,04958 0,91
	2e	0,91 1
			8		1,325 0,91
P-value			8		1,325 0,91	0,6 .
P-value			0,91			0,6 .
			0,91

ГЛАВА 2. СИСТЕМА ОЦЕНКИ СТАТИСТИЧЕСКИХ СВОЙСТВ «DIEHARD»

Данный набор тестов [26] был предложен Джорджем Марсалья (G. Marsaglia) для исследования статистических свойств разработанных им конруэнтных генераторов. Программная реализация тестов вместе с их описанием и необходимыми пояснениями, а также программные реализации конгруэнтных генераторов с описаниями последних опубликованы на специальном компакт-диске

«The Marsaglia random number CDROM», посвященном случайным числам. Содержимое данного диска доступно для свободного ска-

чивания по адресу http://stat.fsu.edu/pub/diehard/.

«DIEHARD» рассматривается как один из наиболее строгих наборов тестов. Связано это с тем, что большинство тестов «DIEHARD» очень сложно «обмануть», то есть сформировать заведомо плохую последовательность, не удовлетворяющую совокупности требований на случайность, но успешно проходящую рассматриваемый тест. Данный факт обусловлен тем, что решение о прохождении или непрохождении теста принимается не на основе частоты появления определенных шаблонов в исследуемой последовательности, а на основе анализа взаимного расположения наборов бит последовательности.

В состав программной системы «DIEHARD» входят следующие тесты:

проверка дней рождения (the birthday-spacing Test);

проверка пересекающихся перестановок (the overlapping k-permutation test);

проверка рангов матриц (the binary rank test for matrices);

обезьяньи тесты (the monkey test);

подсчет единиц (the count-the-1’s test);

тест парковки (the parking lot test);

тест минимальных расстояний (the minimum distance test);

тест случайных сфер (the random spheres test);

тест сжатия (the SQUEEZE test);

тест пересекающихся сумм (the overlapping sums test);

проверка на равномерность (the runs test);

тест игры в кости (the craps test).

Существуют также еще два теста, которые не включены в программную реализацию, но всё-таки относятся к «DIEHARD»:

тест гориллы;

тест НОД (наибольший общий делитель).

Важное замечание. Ряд тестов «DIEHARD» для анализа последовательности применяют критерий χ2 с последующим вычислением P-value (рис. 2.1). Как можно заметить, с увеличением значения статистики теста значение P-value также увеличивается, хотя должно уменьшаться.

Выводимое «DIEHARD» значение представляет собой

		,	2	obs
P-valueDIEHARD 1 P-value , 2 obs 1 igamc		,		obs	.
	2			2
	2			2

Это следует учитывать при интерпретации результатов. P-valueDIEHARD определяет вероятность получения значения, мень-

шего или равного 2 obs для заданного числа степеней свободы. Например, P-valueDIEHARD для 6 (см. рис. 2.1) означает, что результат с 2 obs 9,48 будет получен приблизительно в 85 % случаев. Традиционное значение P-value может быть получено из P-valueDIEHARD при помощи следующей формулы:

P-value 1 P-valueDIEHARD .

И P-value и P-valueDIEHARD могут использоваться при обобщении статистик при помощи критерия Колмогорова–Смирнова. При этом в программе «DIEHARD» используется критерий Андерсона– Дарлинга (как одна из вариаций критерия Колмогорова–Смирнова), однако в выводимой отчетности он фигурирует как критерий Кол- могорова–Смирнова.

BIRTHDAY SPACINGS TEST, M= 512 N=2**24 LAMBDA= 2.0000

Results for bits.01
For a sample of size 500:			mean
bits.01	using bits	1 to 24	1.994
duplicate	number	number
spacings	observed	expected
0	65.	67.668
1	140.	135.335
2	136.	135.335
3	89.	90.224
4	46.	45.112
5	16.	18.045
6 to INF	8.	8.282

Chisquare with 6 d.o.f. =		.54 p-value=			.002747
:::::::::::::::::::::::::::::::::::::::::
For a sample of size 500:				mean
bits.01	using bits		2 to 25	1.954
duplicate	number		number
spacings	observed		expected
0	68.		67.668
1	145.		135.335
2	136.		135.335
3	80.		90.224
4	46.		45.112
5	16.		18.045
6 to INF		9.	8.282
Chisquare with 6 d.o.f. =		2.17 p-value=			.096086
:::::::::::::::::::::::::::::::::::::::::
For a sample of size 500:				mean
bits.01	using bits		3 to 26	1.924
duplicate	number		number
spacings	observed		expected
0	57.		67.668
1	160.		135.335
2	142.		135.335
3	78.		90.224
4	42.		45.112
5	14.		18.045
6 to INF		7.	8.282
Chisquare with 6 d.o.f. =		9.48 p-value=			.851709

Рис. 2.1. Пример отчета о тесте «DIEHARD»

2.1. Проверка дней рождения

Цель теста – проверить равномерность распределения чисел в исходной последовательности, анализируя длины интервалов между числами.

Своим названием тест обязан парадоксу дней рождения (ДР), утверждающему, что если дана группа из 23 и более человек, то вероятность того, что у двоих из них совпадут дни рождения (число и месяц), превышает 50 %.

Пусть = 1, 2,…, n – последовательность m-разрядных чисел.

Если провести аналогию с парадоксом ДР, то представляет собой последовательность из n ДР в году из 2m дней. Применять идеи парадокса ДР непосредственно к числам последовательности нецелесообразно, так как достаточно внедрить в плохую последовательность недостающие элементы, чтобы выровнять статистику и, соответственно, пройти тест. В связи с этим в системе «DIEHARD» анализируются не сами ДР, а промежутки между ними.

Отсортируем числа в порядке неубывания, образовав тем последовательность ДР: Y = y1y2…yn. Сформируем последовательность W

промежутков между ДР:

y2 – y1, y3 – y2, …, yn – yn–1, y1 + 2m – yn.

Последний элемент последовательности Y требует пояснений. Событие y1 после yn наступит только в следующем году, поэтому промежуток между y1 и yn и составляет y1 + 2m – yn.

Пусть ni, i 0, k , – число промежутков, имеющих i дубликатов.

В работе [29] показано, что если ni, i 0, k – число промежутков, встречающихся более, чем 1 раз, то ni асимптотически распределе-

ны по Пуассону с		n3	.
	4	2m

Вычисляем статистику

k	(n	np	)2
2 obs	i	i		,
2 obs		npi		,
i 0		npi

где pi ie . i!

Полученный результат анализируется при помощи критерия 2 с числом степеней свободы, равным k.

Кроме того, вычисляется значение					obs
	k		χ	2
P-value ,χ2 obs P-value k,χ2 obs igamc	k	,	χ			.
P-value ,χ2 obs P-value k,χ2 obs igamc		,				.
	2				2
	2				2

Пример 2.1

Вход:

= 120 75 156 43 97 113 153 61 1 136 54 131 92 167 64 18; m = 8;

n = 16.

Тест:

	Упорядоченные	Промежутки	Упорядоченные
ДР	по возрастанию ДР	между ДР	Упорядоченные
ДР	по возрастанию ДР	между ДР	промежутки между ДР
	Y	W	промежутки между ДР
	Y	W
120	1	90	3
75	18	17	3
156	43	25	5
43	54	11	5
97	61	7	7
113	64	3	7
153	75	11	11
61	92	17	11
1	97	5	11
136	113	16	11
54	120	7	16
131	131	11	17
92	136	5	17
167	153	17	17
64	156	3	25
18	167	11	90

Три промежутка встречаются по одному разу (16, 25, 90), то есть не имеют дубликатов. Таким образом,

n0 = 3.

Число промежутков, имеющих одно повторение (3, 5, 7), равно

n1 = 3.

Промежутки, равные 11 и 17, встречаются 3 и 4 раза соответственно. Таким образом, n2 = 1 и n3 = 1. Однако для достижения пуассоновского распределения необходимо, чтобы значение в катего-

рии превышало 1. Поэтому две категории n2 и n3 объединяются в одну:

n 2 = 2.

	163				4 ,
	4		28		4 ,
	4		28
p0			40	e 4			0,018 ,
p0				0!			0,018 ,
				0!
p		41		e 4			0,073 ,
p							0,073 ,
1				1!
				1!
p 2 1 p0							p1 1 0,018 0,073 0,909 ,
2 obs						3 16 0,018 2		3 16 0,073 2	2 16 0,909 2	39,23 .
2 obs								16 0,073	16 0,909	39,23 .
							16 0,018	16 0,073	16 0,909

Поскольку две категории ( n2 и n3 ) объединены в одну, то вме-

сто трех степеней свободы при вычислении P-value используется две:

P-value ,χ	2	obs P-value 2, 39,230		2		39,23
			igamc		,		0 .
				2		2

В оригинальной реализации данного теста в системе «DIEHARD» используются следующие параметры: m = 24, n = 29. В каждом 32-битном слове анализируются наборы по 24 бита (1–24, 2–25, …, 9–32), находятся 500 длин интервалов между ДР и вычисляется статистика теста, затем полученные 9 статистик анализируются при помощи критерия Колмогорова–Смирнова.

Категории для длин интервалов: n0, n1, n2, n3, n4, n5, n 6. Данное разбиение объясняется следующим. Вероятности для шести и семи совпадений составляют

p6 26 e 2 0,012 , 6!

p7 27 e 2 0,003 . 7!

Для 500 интервалов ожидаемые значения составляют n6ож 500 0,012 6 ,

n7ож 500 0,003 1,5 .

Таким образом, ожидаемое значение для шести совпадений меньше, чем 2, а для достижения пуассоновского распределения необходимо, как уже отмечалось, чтобы ожидаемое значение было больше, чем 2. В связи с этим все длины интервалов, имеющие

шесть и более дубликатов, объединяются в одну категорию n 6. Вероятности и ожидаемое число интервалов для данных катего-

рий следующие:

p0 20 e 2 0,135 , n0ож 500 0,135 67,5 ; 0!

p1 21 e 2 0,270 , n1ож 500 0,270 135 ; 1!

p2 22 e 2 0,270 , n2ож 500 0,270 135 ; 2!

p3 23 e 2 0,180 , n3ож 500 0,180 90; 3!

p4 24 e 2 0,090 , n4ож 500 0,090 45 ; 4!

p5 25 e 2 0,036 , n5ож 500 0,036 18 ; 5!

p 6 1 0,135 0,270 0,270 0,180 0,090 0,036 0,019 ; nож6 500 0,019 9,5 .

Недостатком системы «DIEHARD» является то, что тест ДР в ней анализирует только первые 500 32-битных слов последовательности или 2000 байт. Существуют более строгие реализации данного теста, параметры данных реализаций приведены в табл. 2.1, однако и в самой строгой реализации (m = 32, n = 212) анализируются только первые 5000 32-битных слова или 20 000 байт.

Таблица 2.1. Параметры усиленных тестов дней рождения

m	n	λ
20	28	4
23	29	4
26	210	4
29	211	4
32	212	4
	43

Применение теста к последовательности произвольной длины возможно в случае следования следующим рекомендациям:

значение λ должно лежать в интервале [2, 8];

число категорий должно выбираться таким образом, чтобы ожидаемое значение в каждой категории было не меньше 2.

Однако в данном случае m будет принимать достаточно большие значения, что отрицательно скажется на тестировании генераторов разрядностью много меньше, чем m. Решить данную проблему можно увеличением λ, однако делать это следует с изрядной долей осторожности, поскольку pi 0 , что сделает невозможным

применения критерия 2. Другой вариант – разбить последовательность на подпоследовательности фиксированной длины, удовлетворяющие требованиям к λ, подсчитать для каждой такой подпоследовательности статистики и оценить последние при помощи критерия Колмогорова–Смирнова.

2.2. Проверка пересекающихся перестановок

Цель теста – проверить равномерность распределения чисел в исходной последовательности, анализируя частоты появления наборов из m чисел.

Пусть = 1, 2,…, n – последовательность m-разрядных чисел.

	n 1	пересекающихся наборов по k
Представим ее в виде	N

	k 1

чисел. Лишние числа отбрасываются. В каждом таком наборе воз-

можно k! относительного расположения чисел. Пусть i – число появлений наборов с i-м расположением:

1: j < j + 1 < … < j + k – 1,

2: j < j + k – 2 < j + 1 < … < j + k – 3 < j + k – 1,

…

k!: j + k – 1 < j + k – 2 < … < j;

где j 1, n k 1 – индекс первого элемента набора.

Примечание. В данном тесте предполагается, что в одном наборе нет равных между собой чисел, точнее, вероятность появления данного события настолько мала, что даже если оно всё-таки имеет место, то это никак не сказывается на результатах тестирования

(данный набор просто выбрасывается из рассмотрения). Вычисляем статистику


	i	N 2
k!

2 obs		k!	.

i 1	N

Полученный результат анализируется при помощи критерия 2 с числом степеней свободы, равным k! – 1.

Кроме того, вычисляется значение

	k! 1		χ	2	obs
P-value ,χ2 obs P-value k! 1,χ2 obs igamc	k! 1	,	χ		obs	.
P-value ,χ2 obs P-value k! 1,χ2 obs igamc		,				.
	2				2
	2				2

Пример 2.2

Вход:

n = 28; m = 3; k = 3.

Тест:

N28 1 13 .

3 1

Последнее число (2) не входит в состав ни одного набора, поэтому отбрасываем его.

Получаем следующие пересекающиеся наборы:

{0, 2, 4} {4, 7, 3} {3, 5, 1} {1, 6, 2} {2, 0, 5} {5, 1, 4} {4, 6, 3} {3, 0, 6} {6, 3, 5} {5, 6, 3} {3, 2, 1} {1, 6, 7} {7, 3, 7}.

Если набор имеет вид {x1, x2, x3}, то распределение по категориям будет следующим:

1: x1 < x2 < x3,2: x1 < x3 < x2,3: x2 < x1 < x3,4: x2 < x3 < x1,5: x3 < x1 < x2,6: x3 < x2 < x1.

Исходя из этого, получаем

1 = 2: {0, 2, 4} и {1, 6, 7},2 = 1: {1, 6, 2},3 = 2: {2, 0, 5} и {3, 0, 6},

4 = 2: {5, 1, 4} и {6, 3, 5},5 = 4: {4, 7, 3}, {3, 5, 1}, {4, 6, 3}, {5, 6, 3},6 = 1: {3, 2, 1}.

Примечание. Набор {7, 3, 7} не рассматривался, так как в нем встречаются два повторяющихся числа. Предполагается, что вероятность данного события настолько мала, что не оказывает влияния на результаты прохождения теста.

				2	13	2			13	2	2		13	2	2		13	2	4		13	2
				2	3!		1		3!		2		3!		2		3!		4		3!
2 obs					3!				3!				3!				3!				3!
				13				13				13				13				13
				3!					3!			3!				3!				3!
		13	2
1		3!
		3!		2,84.
	13

P-value ,χ2 obs P-value 3! 1; 2,84 0,725 .

В системе «DIEHARD» данный тест имеет название OPERM5 – overlapping 5-permutation. Анализируемая последовательность представляется в виде двух подпоследовательностей, состоящих из N = 1 000 000 пересекающихся наборов по пять 32-разрядных чисел (таким образом, длина тестируемой последовательности составляет

2 4 (1 000 000 4 + 1) = 32 000 008 байт). Следуя введенным обо-

значениям, m = 32, k = 5, n = 2 (1 000 000 4 + 1) = 8 000 002.

Недостатком системы «DIEHARD» является фиксированная длина последовательности для данного теста и ориентированность на 32-разрядные генераторы.

2.3. Проверка рангов матриц

Цель теста – проверить равномерность распределения чисел в исходной последовательности, анализируя частоты появления матриц различных рангов.

1 2 j i

Пусть = 1, 2,…, n – последовательность m-разрядных чисел.

		n	двоичных матриц размером Q R.
Представим ее в виде	N

	Q R

Лишние числа отбрасываем.

Подсчитываем ранги матриц. Пусть i – число матриц ранга i, i 1, min Q, R . Вычисляем статистику

2 obs	min Q, R	i	Np	2
			i		.

	i 1		Npi

Значения соответствующих вероятностей можно определить по следующей формуле [4, 18, 31]:

pi 2i Q R i QR i 1 1 2 j Q 1 2 j R . j 0

Полученный результат анализируется при помощи критерия 2 с числом степеней свободы, равным min(Q, R) –1.

Кроме того, вычисляется значение

P-value ,χ2 obs P-value min(Q, R) 1,χ2 obs

			χ	2	obs
min(Q, R) 1			χ		obs
igamc	2	,				.
igamc		,			2	.
					2

Пример 2.3

Вход:

= A25Сh 24B1h E923h

Разбиение на матрицы 4 4:

Исходная последовательность в двоичном представлении:

= 1010 0010 0101 1100 0010 0100 1011 0001 1110 1001 0010 0011.

Представим каждое число в виде матрицы

	1	0	1	0		0	0	1	0		1	1	1	0
	1	0	1	0		0	0	1	0		1	1	1	0
A25Ch	0	0	1	0	24B1h	0	1	0	0	E923h	1	0	0	1
	0	1	0	1		1	0	1	1		0	0	0	1
	1	1	0	0		0	0	0	1		0	0	1	1
						47

В системе «DIEHARD» реализовано 3 разновидности данного теста.

Проверка рангов матриц 32 32. Последовательность 32-

разрядных чисел рассматривается как N = 40 000 матриц размером

32 32. Формирование матриц происходит следующим образом: берутся наборы по 32 числа, двоичное представление первого числа – первая строка матрицы, второго – вторая и т.д. Анализируются следующие ранги матриц: 32, 31, 30 и меньшие либо равные 29.

Длина последовательности для тестирования равна 40 000 32 4 = = 5 120 000 байт. Вероятности и ожидаемое число матриц для данного теста следующие:

p32 232 32 32 32 32 32

1 2

j 32

0,289;

32 1

j 0

1 2 j 32

n32ож 40 000 p32

11 551,524 ;

1 2

0,578;

p31 231 32 32 31 32 32 1 2

j 32

31 1

j 0

1 2 j 31

n31ож 40 000 p31

23 103,048 ;

1 2

0,128;

p30 230 32 32 30 32 32

1 2

j 32

30 1

j 0

1 2 j 30

n30ож 40 000 p30

5 134,010 ;

p 29

1 p32

p31

p30

1 0,289 0,578 0,128 0,05 ;

nож

40 000 p

211,418 .

Проверка

рангов

матриц

31 31. Последовательность

32-разрядных чисел рассматривается как N = 40 000 матриц разме-

ром 31 31. Формирование матриц происходит следующим образом: берутся наборы по 32 числа, первые 31 бит первого числа – первая строка матрицы, первые 31 бит второго – вторая и т.д. Анализируются следующие ранги матриц: 31, 30, 29 и меньшие либо равные 28. Минимальная длина последовательности равна

40 000 32 4 = 5 120 000 байт.

Вероятности и ожидаемое число матриц для данного теста сле-

дующие:

p31

231 31 31 31 31 31 1 2

j 31

1 2

j 31

0,289;

31 1

j 0

1 2 j 31

nож

40 000 p

11 551,523 ;

1 2

0,578;

p30

230 31 31 30 31 31

j 31

30 1

j 0

1 2 j 30

nож

40 000 p

23103,048 ;

1 2

0,128;

p29

229 31 31 29 31 31

j 31

29 1

j 0

1 2 j 29

n29ож 40 000 p29

5134,010 ;

p 28 1 p31

p30

p29

1 0,289 0,578 0,128 0,05 ;

nож

40 000 p

211,419 .

Проверка

рангов

матриц

6 8.

Последовательность

32-разрядных чисел рассматривается как N = 100 000 матриц раз-

мером 6 8. Формирование матриц происходит следующим образом: берутся наборы по 6 чисел, первые 8 бит первого числа – первая строка матрицы, первые 31 бит второго – вторая и т.д. Анализируются следующие ранги матриц: 6, 5 и меньшие либо равные 4.

Минимальная длина последовательности равна 100 000

6 4 =

= 2 400 000 байт.

Вероятности и ожидаемое число матриц для данного теста сле-

дующие:	6 8		1 2			1 2		0,773 ;
p6 26 6 8 6				j	6		j 8
	6 1
	j 0		1 2 j 6
n6ож 100 000 p6			77 311,764 ;					0,217 ;
p5 25 6 8 5	6 8		1 2	j	6	1 2	j 8
	5 1
	j 0		1 2 j 5
nож 100 000 p		5	21 743,933 ;
5
p 4 1 p6 p5 1 0,73 0,217 0,010 ;
nож 100 000 p			944,303 .
4	4						49

Недостаток данного теста в системе «DIEHARD» – фиксированная длина анализируемой последовательности. При этом сам тест достаточно просто модифицируется для матриц произвольного размера (что позволяет анализировать генераторы с произвольной разрядностью), а также для последовательностей произвольной длины.

2.4. Обезьяньи тесты

Цель тестов – проверить равномерность распределения чисел в исследуемой последовательности на основе анализа отсутствующих в ней подпоследовательностей.

Столь странному названию данные тесты [32] обязаны своему автору – Дж. Марсалья, который предложил рассматривать генератор как обезьяну, печатающую на машинке с определенным набором символом, и анализировать количество пропущенных слов в выдаваемой последовательности. Вполне вероятно, что при именовании теста была проведена параллель с теоремой о бесконечных обезьянах, утверждающей, что абстрактная обезьяна, ударяя случайным образом по клавишам печатной машинки, рано или поздно намечает заранее заданный текст, то есть вероятность наступления данного события будет стремиться к единице при стремлении времени печатания к бесконечности.

Пусть = 1, 2,…, n – последовательность m-разрядных чисел. Преобразуем ее в строку *, состоящую из N слов. Каждое слово состоит из k l-разрядных букв (буквы и слова в исходной последовательности не обязательно следуют друг за другом). Тогда число отсутствующих слов в строке * аппроксимируется с нормальным распределением со средним

		ож		2kl e		N
						2kl
						2kl
и отклонением
	2l	2l	2l				,
			... cov ni1 ,ni2 , ...,nik				,
	i1 1 i2 1		ik 1
				i	, присутствует в слове;
где ni 1, еслибуква, равная2					, присутствует в слове;

0, еслибуква, равная2i , отсутствует в слове.

Вычисление является в ряде случаев проблематичным, поэтому на практике используют либо табличные значения, либо значения, полученные в результате ряда экспериментов.

Результаты теста оцениваются путем вычисления статистики для нормированной нормальной величины

P-value P-value , ож, ;

		ож

P-value X , , P-value , ож,	erfс	2
		2	,
		2	,
		2

где μ – число отсутствующих слов.

Недостаток данного теста в системе «DIEHARD» – фиксированная длина анализируемой последовательности. Попытка модифицировать тест для анализа последовательности произвольной длины осложняется проблематичностью вычисления σ.

В системе «DIEHARD» реализованы следующие представители данной группы тестов.

Проверка потока бит (The bitstream test). Представим исход-

ную последовательность 32-разрядных чисел = 1, 2,…, n в виде последовательности бит b = b1,b2,…,b32n. Преобразуем b в строку, состоящую из 20-буквенных пересекающихся слов (1 буква – 1 бит). Получим:

b1b2…b20, b2b3…b21, …, b32n-19b32n-18…b32n.

Тогда в строке, состоящей из 221 пересекающихся 20-буквенных слов, число отсутствующих слов аппроксимируется с нормальным

распределением с ож = 141 909 и = 428. Тест повторяется 20 раз (1-й раз – отсчет начинается с 1-го бита, 2-й – с (221 + 1)-го и т.д. до

20-го). Для каждого случая определяется число отсутствующих слов μ и вычисляется статистика для нормированной нормальной величины:

		141 909
	erfс	2 428
P-value X , , P-value , 141 909, 428			.
		2

К полученным статистикам применяется критерий Колмогоро- ва–Смирнова.

Следуя введенным обозначениям, N = 221, k = 20, l = 1.

Длина тестируемой последовательности равна 221 20 бит = = 5 242 800 байт.

Пример 2.4

Вход:

= 5 2 0 7; N = 10;

k = 3; l =1.

Тест:

Исходная строка в битовом представлении: b = 101 010 000 111,

Слова: {101}, {010}, {101}, {010}, {100}, {000}, {000}, {001}, {011}, {111},

Число отсутствующих слов равно 1 {110} (предполагается, что всего возможно 23 8 слов от {000} до {111}).

Проверка разреженных пересекающихся пар (OPSO – Over- lappng-Pairs-Sparce-Occupancy). Пусть = 1, 2,…, n – исходная последовательность 32-разрядных чисел. Из каждого числа выбираем 10 бит (букву) и образуем двухбуквенные слова. Тогда в строке из 221 пересекающихся слов число отсутствующих слов аппрок-

симируется с нормальным распределением с = 141 909 и = 290. Тест повторяется 23 раза (1-й раз – выбираются биты с 1-го по 10- й, 2-й – со 2-го по 11-й и т.д. до 23-го). Для каждого случая определяется число отсутствующих слов μ и вычисляется статистика для нормированной нормальной величины:

		141 909
	erfс	2 290
P-value X , , P-value , 141909, 290			.
		2

К полученным статистикам применяется критерий Колмогоро- ва–Смирнова.

Следуя введенным обозначениям, N = 221, k = 2, l = 10.

Длина тестируемой последовательности равна (221 + 1) 4 = = 8 388 612 байт.

Пример 2.5

Вход:

= 15 12 0 7 9 4 1 13 10 8 4 3 0 8; N = 13;

k = 2; l = 2.

Тест:

1-й раз выбираются первые 2 бита каждого числа:

b = 1111 1100 0000 0111 1001 0100 0001 1101 1010 1000 0100 0011 0000 1000, Слова: {1111}, {1100}, {0001}, {0110}, {1001}, {0100}, {0011},

{1110}, {1010}, {1001}, {0100}, {0000}, {0010}.

Число отсутствующих слов равно 5: {0101}, {0111}, {1000},

{1011}, {1101} (предполагается, что всего возможно 24 16 слов от {0000} до {1111}).

2-й раз выбираются вторые 2 бита каждого числа:

b = 1111 1100 0000 0111 1001 0100 0001 1101 1010 1000 0100 0011 0000 1000, Слова: {1110}, {1000}, {0011}, {1100}, {0010}, {1000}, {0010},

{1001}, {0100}, {0010}, {1001}, {0100}, {0000}.

Число отсутствующих слов равно 8: {0001}, {0101}, {0110}, {0111}, {1010}, {1011}, {1101}, {1111}.

Проверка разреженных пересекающихся четверок (Overlap- ping-Quadruples-Sparse-Occupancy). Пусть = 1, 2,…, n – исход-

ная последовательность 32-разрядных чисел. Из каждого числа выбираем 5 бит (букву) и образуем 4-буквенные слова. Тогда в строке из 221 пересекающихся слов число отсутствующих слов аппроксимируется с нормальным распределением с = 141 909 и = 339. Тест повторяется 28 раз (1-й раз – выбираются биты с 1-го по 5-й, 2-й – со 2-го по 6-й и т.д. до 28-го). Для каждого случая определяется число отсутствующих слов μ и вычисляется статистика для нормированной нормальной величины:

		141 909
	erfс	2 339
P-value X , , P-value ,141 909, 339		2 339	.
P-value X , , P-value ,141 909, 339		2	.
		2
53

К полученным статистикам применяется критерий Колмогоро- ва–Смирнова.

Следуя введенным обозначениям, N = 221, k = 4, l = 5.

Длина тестируемой последовательности равна (221 + 3) 4 = = 8 388 620 байт.

Пример 2.6

Вход:

= 7 6 0 3 4 2 0 6 5 4 2 1 0 4 7 3; N = 5;

k = 4; l = 1.

Тест:

1-й раз выбираются первые биты каждого числа:

b = 111 110 000 011 100 010 000 110 101 100 010 001 000 100 111 011, Слова: {1100}, {0100}, {0111}, {1000}, {0110}.

Предполагается, что всего возможно 24 16 слов, поэтому число отсутствующих слов равно 16 – 5 = 11.

2-й раз выбираются вторые биты каждого числа:

b = 111 110 000 011 100 010 000 110 101 100 010 001 000 100 111 011, Слова: {1101}, {1010}, {0100}, {0100}, {0011}.

Одно слово встречается два раза ({0100}), поэтому число отсутствующих слов равно 16 – (5 – 1) = 12.

Проверка разреженных пересекающихся десяток (DNA).

Пусть = 1, 2,…, n – исходная последовательность 32-разрядных чисел. Из каждого числа выбираем 2 бита (букву) и образуем 10-буквенные слова. Тогда в строке из 221 пересекающихся слов число отсутствующих слов аппроксимируется с нормальным рас-

пределением с = 141 909 и = 339. Тест повторяется 31 раз (1-й раз – выбираются биты с 1-го по 2-й, 2-й – со 2-го по 3-й и т.д. до 31-го). Для каждого случая определяется число отсутствующих слов μ и вычисляется статистика для нормированной нормальной величины:

		141 909
	erfс	2 339
P-value X , , P-value , 141909, 339			.
		2

К полученным статистикам применяется критерий Колмогоро- ва–Смирнова.

Следуя введенным обозначениям, N = 221, k = 2, l = 10.

Длина тестируемой последовательности равна (221 + 9) 4 = = 8 388 644 байт.

Примечание. Указанные тесты можно существенно усилить, если изменить порядок выбора бит для составления слов или тестировать слова с определенной периодичностью.

2.5. Подсчет единиц

Цель теста – проверить равномерность распределения чисел в исследуемой последовательности на основе анализа частоты появления байтов с различным числом единиц.

Пусть = 1, 2,…, n – исходная последовательность 32разрядных чисел. Представим ее в виде последовательности байт b = b1,b2,…,b4n. Каждый байт может содержать от 0 до 8 единиц с ве-

роятностями 2561 , 2568 , 25628 , 25656 , 25670 , 25656 , 25628 , 2568 , 2561 со-

ответственно. Введем следующие обозначения: если байт содержит от 0 до 2 единиц, обозначим его A, 3 единицы – B, 4 единицы – C, 5 единиц – D, от 6 до 8 единиц – Е. Соответствующие вероятности:

	8		8			8


p A	0		1			2	1 8 28	37	,
		256					256	56
	8

			56
p B	3		56	,
p B			256	,
256			256
	8

			70
p С	4		70		,
p С			256		,
256			256

p D 5 56 , 256 256

	8		8	8

	6		7	8	28 8 1	37
p E	6		7	8	28 8 1	37	.
p E					256	256	.
		256			256	256

Представим последовательность b в виде строки из N пересекающихся k-буквенных слов. Пусть ik , i 1, 5k , – число появлений слова конкретного типа (например, 15 – число появлений слова

ААААА, …, 53125 – число появлений слова EEEEE). Вычисляем статистику

5k	k	k	2	5k 1	k 1	k 1	2
2 obs	i	Npi			i	Npi		,
2 obs		Npk			Npk 1			,
i 1		Npk		i 1	Npk 1
		i				i

которая аппроксимируется с распределением 2 с числом степеней свободы, равным 5k – 5k–1 ( pik – вероятность появления слова ik ).

Вычисляем значение

P-value , χ2 obs P-value 5k 5k 1, χ2 obs

	5	k	5	k 1		χ	2	obs		.
igamc	5		5			χ		obs
					,				.
					,				.
			2					2
			2					2

В системе «DIEHARD» используются следующие параметры:

N = 256 000, k = 5.

Длина тестируемой последовательности равна 256 000 4 + 1 = = 1 024 001 байт.

Пример 2.7

Вход:

= C700h A4C9h 2367h E4B7h; k = 3;

N = 3.

Формирование слов:

b = 11000111 0000000 10100100 11001001 00100011 01100111 11100100 10110111,

b = E A B C B D C E.

Слова: {EAB}, {BCB}, {BDC}.

Расширением данного теста является Подсчет единиц в опре-

деленных байтах (the count-the-1’s for specific bytes). Рассматри-

вается последовательность 32-разрядных чисел и из каждого числа выбирается 8 бит, которые затем участвуют в образовании слов. Тест повторяется 25 раз (1-й раз – выбираются биты с 1-го по 8-й, 2-й – со 2-го по 9-й и т.д. до 25-го). К полученным статистикам применяется критерий Колмогорова–Смирнова.

Длина тестируемой последовательности равна 4 (256 000 4 + + 1) = 4 096 004 байт.

Пример 2.8

Вход:

= C700h A4C9h 2367h E4B7h 4D20h 128Ah BB47h 98C3h 3AC6h; k = 3;

N = 2.

Формирование слов:

Биты с 1-го по 8-й:

b = 11000111 00000000 10100100 11001001 00100011 01100111 11100100 10110111 01001101 00100000 00010010 10001010 10111011 01000111 10011000 11000011 00111010 11000110.

Слова: {DBC}, {CEC}.

Биты со 2-го по 9-й:

b = 11000111 00000000 10100100 11001001 00100011 01100111 11100100 10110111 01001101 00100000 00010010 10001010 10111011 01000111 10011000 11000011 00111010 11000110.

Слова: {СBC}, {CDD}.

2.6. Тест парковки

Цель теста – проверить равномерность распределения чисел в исследуемой последовательности на основе анализа корреляции между элементами последовательности.

Как и ряд других тестов «DIEHARD», тест парковки связан с некоторой задачей теории вероятностей и математической статистики. В данном случае речь идет о задаче парковки. Суть ее в сле-

дующем. В квадрате размером 100 100 случайно паркуются (размещаются) «автомобили» – окружности радиусом 1. Для того чтобы избежать вопросов доставки до места парковки автомобиля, последний предлагается заменить средством передвижения, не зависимым от пробок, например вертолетом. Каждая попытка может закончиться столкновением или удачной парковкой. В случае столкновения средство передвижения продолжает попытки размещения до тех пор, пока не осуществит удачную парковку. Пусть X – число удачных парковок после p = 12 000 попыток. Эксперименты показывают, что X асимптотически нормально распределено с

μ = 3 523 и σ = 21,9.

Сразу следует отметить: поскольку закон распределения числа удачных парковок получен экспериментально, значения p, μ и σ строго фиксированы.

Пусть = 1, 2,…, n – исходная последовательность m- разрядных чисел. Разбиваем исходную последовательность на N подпоследовательностей, состоящих из 2p m-разрядных чисел. Лишние числа отбрасываются. В качестве координат места парковки выступают нормированные значения соседних чисел подпоследовательности. Таким образом, для p попыток координаты мест парковки будут иметь вид

															2 p 1		2 p
100		1	;100		2	,			3			4	, … ,
100	2	m	;100	2	m	,	100	2	m	;100	2	m	, … ,	100	2	m ;100	2	m	.
	2			2				2			2				2		2

Как можно заметить, значение m должно быть больше либо равно log2 100 7 , чтобы обеспечить равномерное заполнение

квадрата.

Пример 2.9

Вход:

= 25, 36, 127, 200; m = 8.

Формирование координат мест для парковки:

1-е место очередной парковки:

	25	;100	36	9,765625; 14,0625 .
100	8	;100	8	9,765625; 14,0625 .
	2		2

2-е место очередной парковки:

	127	; 100	200		49,609375; 78,125 .
100	8	; 100	2	8	49,609375; 78,125 .
	2		2

Подсчитывается число удачных парковок X. Делается это при помощи следующего алгоритма:

Шаг 1. Установить Х в 0, i в 0.

Шаг 2. Выбрать очередную координату. Увеличить i на 1. Если i

>p, то перейти на Шаг 5, в противном случае перейти на Шаг 3. Шаг 3. Если координата уже встречалась, то перейти на Шаг 2,

впротивном случае перейти на Шаг 4.

Шаг 4. Увеличить Х на 1. Перейти на Шаг 2. Шаг 5. Конец.

Пример 2.10

Вход:

Координаты: (1; 3), (2; 4), (4; 2), (7; 8), (5; 6), (2; 4), (9; 1), (4; 2), (5; 6), (1; 1);

p = 10.

Тест:

i	Координаты,	Очередная	X
i	которые уже встречались	координата	X
	которые уже встречались	координата

0		-	0
1		(1; 3)	1
2	(1; 3)	(2; 4)	2
3	(1; 3), (2; 4)	(4; 2)	3
4	(1; 3), (2; 4), (4; 2)	(7; 8)	4
5	(1; 3), (2; 4), (4; 2), (7; 8)	(5; 6)	5
6	(1; 3), (2; 4), (4; 2), (7; 8), (5; 6)	(2; 4)	5
7	(1; 3), (2; 4), (4; 2), (7; 8), (5; 6)	(9; 1)	6
8	(1; 3), (2; 4), (4; 2), (7; 8), (5; 6), (9; 1)	(4; 2)	6
9	(1; 3), (2; 4), (4; 2), (7; 8), (5; 6), (9; 1)	(5; 6)	6
10	(1; 3), (2; 4), (4; 2), (7; 8), (5; 6), (9; 1)	(1; 1)	7

Для числа удачных парковок вычисляется статистика для нормированной нормальной величины:

				X 3 523

			erfс
				2 21,9
P-value X , , P-value Х; 3 523; 21,9					.
				2

В системе	«DIEHARD» анализируются	N = 10 наборов по
2 p 2 12 000	32-разрядных чисел (m = 32). Для каждого набора

вычисляется значения P-value. К полученным статистикам применяется критерий Колмогорова–Смирнова.

Длина тестируемой последовательности равна 10 (2 12 000 4) = = 960 000 байт.

2.7. Тест минимальных расстояний

Данный тест развивает идеи теста парковок. Теперь анализируется не только координаты точек, но и их взаимное расположение на плоскости.

Рассмотрим вначале соответствующую тесту задачу. В квадрате размером 10000 10000 размещается p = 8 000 случайных точек.

		p		p	2	p
Вычисляется dmin	– минимальное расстояние из						воз-

			2			2

можных между парами точек. Если точки в квадрате расположены случайно, то квадрат минимального расстояния между точками асимптотически экспоненциально распределен со средним 0,995. Следовательно, величина

			d 2
	k 1 e		0,995

нормировано нормально распределена на интервале 0,1 . Таким

образом, получив N таких величин, можно применить критерий Колмогорова–Смирнова и вычислить значение P-valueКС.

Теперь рассмотрим саму реализацию теста. Пусть = 1, 2,…, n – исходная последовательность m-разрядных чисел. Разбиваем исходную последовательность на N подпоследовательностей, состоящих из 2p m-разрядных чисел. Лишние числа отбрасываются. В качестве координат точек выступают нормированные значения

соседних чисел подпоследовательности. Таким образом, для i-й подпоследовательности, i 1, N , координаты p точек будут иметь вид

		2 p i 1 1							2 p i 1 2

					m		;10 000					m
10000			2		m		;10 000				2	m			,
			2								2
			2 p i 1 3								2 p i		1 4
			2 p i 1 3				; 10 000				2 p i		1 4
10 000																,
10 000			2		m						2		m			,
			2								2
						…
	2 p i 1 2 p 1									2 p i 1 2 p
								;10 000
				m										m
10 000			2	m								2		m			.
			2									2

Как можно заметить, значение m должно быть больше либо равно log2 10 000 14 , чтобы обеспечить равномерное заполнение

квадрата.

Для каждой подпоследовательности вычисляем квадрат мини-


мального расстояния	d 2	между из		p2 p			возможных между па-
мального расстояния	d 2	между из					возможных между па-
	mini		2
			2
рами точек и значение статистики
			d 2
	ki 1 e		mini
			0,995 , i			,
			0,995 , i		1, N	,

после чего применяем к значениям ki критерий Колмогорова–

Смирнова для получения значения P-valueКС.

Примечание. Для ускорения поиска квадрата минимального расстояния между точками рекомендуется воспользоваться свойством треугольника, гласящим, что сумма двух сторон не может быть больше третьей, и для очередной пары точек вначале сравнивать квадрат минимального расстояния с квадратом разности между координатами по одной из осей и только в случае превышения рассчитывать квадрат разности между координатами по другой оси.

Пример 2.11

Вход:

Координаты (1; 9), (4; 2), (2; 4), (7; 8). p = 4.

Сторона квадрата равна 10.

Тест:

В качестве исходного квадрата минимального расстояния установим максимально возможное значение, т.е. значение в случае, когда точки анализируемой пары лежат в диаметрально противо-

положных сторонах квадрата. В этом случае dmin2 102 102 200 .

Всего возможно 422 4 6 расстояний. Найдем минимальное из них.

		2	Точка	Точка	xAB2	yAB2			dAB2			Новое
	№	dmin	A	B	xA xB 2	yA yB 2			xAB2		yAB2	dmin2
	1	200	(1; 9)	(4; 2)	9 < 200	49	<	200	58	< 200		58
	2	58	(1; 9)	(2; 4)	1 < 58	25 < 58			26 < 58			26
	3	26	(1; 9)	(7; 8)	36 > 26		-				-	-
	4	26	(4; 2)	(2; 4)	4 < 26	4	<	26	8	< 26		8
	5	8	(4; 2)	(7; 8)	9 > 8		-				-	-
	6	8	(2; 4)	(7; 8)	25 > 8		-				-	-
dmin2		8 .

В системе «DIEHARD» анализируются N = 100 наборов по 2 p 2 8 000 32-разрядных чисел (m = 32).

Длина тестируемой последовательности равна 100 (2 8 000 4) = = 6 400 000 байт.

2.8. Тест случайных сфер

Данный тест продолжает линейку тестов, связанных с оценкой корреляции, и развивает идеи теста парковок и теста минимальных расстояний. Теперь анализируется взаимное расположение точек в пространстве.

Соответствующая задача звучит следующим образом. В кубе со стороной 1000 выбирается p = 4000 случайных точек. Каждая точка представляет собой центр сферы, радиус которой – минимальное

расстояние от центра сферы до ближайшей к центру точки. Если точки в кубе расположены случайно, то объем минимальной такой сферы асимптотически экспоненциально распределен со средним

120 . Таким образом, кубическое значение радиуса r3			мини-
3		min
3
	r3
k 1 e	min
k 1 e	30
мальной сферы асимптотически экспоненциально распределено со
средним, равным 30.
Следовательно, величина
нормировано нормально распределена на интервале 0, 1 .			Таким

образом, получив N таких величин, можно применить критерий Колмогорова–Смирнова и вычислить значение P-valueКС.

Теперь рассмотрим саму реализацию теста. Пусть = 1, 2,…, n – исходная последовательность m-разрядных чисел. Разбиваем исходную последовательность на N подпоследовательностей, состоящих из 3p m-разрядных чисел. Лишние числа отбрасываются. В качестве координат центров окружностей выступают нормированные значения соседних чисел подпоследовательности. Таким

образом, для i-й подпоследовательности, i 1, N , координаты p точек будут иметь вид

3 p i 1 1

3 p i 1 2

3 p i 1 3

;1000

1000

3 p i 1 4

3 p i 1 5

;1000

1000

…

				3 p i 1 3 p 2					3 p i 1 3 p 1			3 p i 1 3 p
								;1000			;1000
						m				m			m
	1000				2	m			2	m		2	m	.
					2				2			2
	Как можно заметить, значение m должно быть больше либо
равно	log	2	1000		10		, чтобы обеспечить равномерное заполнение
		2

куба.

Пример 2.12

Вход:

= 368, 442, 543, 200, 712, 956; m = 10.

Формирование координат центров окружностей:

центр 1-й окружности:

	368	; 1000	442	; 1000	543
1000	10	; 1000	10	; 1000	10
	2		2		2
359,375; 431,640625; 530,2734375 ;
центр 2-й окружности:
	200	;1000	712	; 1000	956
1000	10	;1000	10	; 1000	10
	2		2		2
195,3125; 431,640625; 530,2734375 .

Для каждой подпоследовательности вычисляем минимальный

			p		2
	3		p		p p
	3				p p
кубический радиус	rmini	для всех					возможных сфер и
кубический радиус	rmini	для всех		2		2	возможных сфер и
				2		2

значение статистики

	r3
ki 1 e	mini	, i		,
ki 1 e	30	, i	1, N	,

после чего применяем к значениям ki критерий Колмогорова–

Смирнова для получения значения P-valueКС.

Примечание. Для ускорения вычислений рекомендуется сначала найти квадрат минимального радиуса. В этом случае можно использовать подход, примененный в тесте проверки парковок – последовательно сравнивать значение квадрата минимального радиуса с квадратом разницы координат по каждой из осей и только в случае превышения в каждом случае вычислять значение куба радиуса.

Пример 2.13

Вход:

Координаты (1; 9; 7), (4; 2; 6), (2; 4; 5), (7; 8; 4); p = 4;

Сторона куба равна 10.

Тест:

В качестве исходного квадрата минимального радиуса установим максимально возможное значение, т.е. значение в случае, когда точки анализируемой пары лежат в диаметрально противополож-

ных сторонах куба. В этом случае rmin3 102 102 102 300 .

Всего возможно 42 2 4 6 радиусов. Найдем минимальный из них.

rmin2

Точка A

Точка B

xAB2

yAB2

zAB2

rAB2

Новое

rmin

200

(1; 9; 7)

(4; 2; 6)

9 < 300

49 < 300

1 < 300

59 < 300

(1; 9; 7)

(2; 4; 5)

1 < 59

25 < 59

4 < 59

30 < 59

(1; 9; 7)

(7; 8; 4)

36 > 26

(4; 2; 6)

(2; 4; 5)

4 < 30

1 < 30

9 < 30

(4; 2; 6)

(7; 8; 4)

9 = 9

(2; 4; 5)

(7; 8; 4)

25 > 9

xAB2 xA xB 2 , yAB2

yA yB 2 , zAB2

zA zB 2 ,

r 2

z2 .

rmin2 9 rmin3 27 .

В системе «DIEHARD» анализируются N = 20 наборов по 3 p 2 4000 32-разрядных чисел (m = 32).

Длина тестируемой последовательности равна 20 (3 8 000 4) = = 1 920 000 байт.

2.9. Тест сжатия

Цель теста – проверить равномерность распределения чисел в исследуемой последовательности на основе анализа взаимного расположения чисел.

Пусть = 1, 2,…, n – исходная последовательность 32разрядных чисел. Преобразуем ее в последовательность * чисел, нормированных на интервале 0;1

* 2321 , 2322 ,..., 232n .

Пример 2.14

Вход:

ε = 25 356 578, 13 047 856; n = 2.

* 25 356 578	,13 047 856
232	232
0,0054846932180225849151611328125;
0,0030379407107830047607421875

Для каждого элемента последовательности * подсчитывается число итераций, необходимое для уменьшения k = 231 = = 2 147 483 648 до 1 при помощи преобразования

k k X .

Определяются значения Ys – количество уменьшений с числом итераций, равным s, s 6, 48 (в Y6 записывается количество

уменьшений с числом итераций, меньшим либо равным 6; в Y48 записывается количество уменьшений с числом итераций, большим либо равным 48).

Пример 2.15

Вход:

ε = 250, 32, 137, 68, 190, 94, 73, 201;

разрядность чисел = 8; k 127 .

Тест:

*									0,9765625; 0,125;

	28	28	28	28	28	28	28	28

0,53515625; 0,265625; 0,7421875; 0,3671875; 0,28515625; 0,78515625.

s	k	X	k X	k X
1	127	0,9765625	124,0234375	125
2	125	0,125	15,625	16
3	16	0,53515625	8,5625	9
4	9	0,265625	2,390625	3
5	3	0,7421875	2,2265625	3
6	3	0,3671875	1,1015625	2
7	2	0,28515625	0,5703125	1

Увеличиваем значение Y7 на 1.

Полученные значения анализируются при помощи критерия 2 с42 степенями свободы

48	Y	np	s	2
χ2 obs	s		s		,
χ2 obs		nps			,
s 6		nps

где n – количество чисел, вовлеченных в процесс нахождения значений Ys, s 6, 48 . Значения ожидаемых вероятностей приведены в табл. 2.2.

Таблица 2.2. Ожидаемые значения для вероятностей ps , s 6, 48

s = 6	s = 7	s = 8	s = 9	s = 10	s = 11	s = 12	s = 13
21,03	57,79	175,54	467,32	1107,83	2 367,84	4 609,44	8 241,16

s = 14	s = 15	s = 16	s = 17	s = 18	s = 19	s = 20	s = 21
13 627,81	20 968,49	30 176,12	40 801,97	52 042,03	62 383,28	72 056,37	78 694,51

s = 22	s = 23	s = 24	s = 25	s = 26	s = 27	s = 28	s = 29
82 067,55	81 919,35	78 440,08	72 194,12	63 986,79	54 709,31	45 198,52	36 136,61

s = 30	s = 31	s = 32	s = 33	s = 34	s = 35	s = 36	s = 37
28 000,28	21 055,67	15 386,52	10 940,20	7 577,96	5 119,56	3 377,26	2 177,87

s = 38	s = 39	s = 40	s = 41	s = 42	s = 43	s = 44	s = 45
1 374,39	849,70	515,18	306,66	179,39	103,24	58,51	32,69

s = 46	s = 47	s = 48
18,03	9,82	11,21

			67

Также вычисляется статистика			obs
	42 ,	2
P-value ,χ2 obs P-value 42, 2 obs igamc	42 ,			.
	2		2
	2		2

2.10. Проверка пересекающихся сумм

* 2321 , 2322 ,..., 232n .

Последовательность * разбивается на N подпоследовательностей *i , i 1,n , состоящих из 2 p 1 слов. Лишние слова отбрасы-

ваются. Для каждой подпоследовательности *i				формируется p
сумм:
S	*	*	... *	,
1	2 p i 1 1	2 p i 1 2	2 p i 1 p
		…
S p 2 p i 1 p 2 p i 1 p 1			... *2 p i 1 2 p 1 .

Пример 2.16

Вход:

ε* = 0,25; 0,32; 0,137; 0,68; 0,19; 0,94; 0,73; 0,201; 0,198; 0,98; p = 5.

Тест:

Число 0,98 отбрасываем, как не использующееся в тесте.

S1 0,25 0,32 0,137 0,68 0,19 1,577 ,

S2 0,32 0,137 0,68 0,19 0,94 2,267 ,

S3 0,137 0,68 0,19 0,94 0,73 2,677 ,

S4 0,68 0,19 0,94 0,73 0,201 2,741,

S5 0,190 0,94 0,73 0,201 0,198 2,259 .

Если числа последовательности случайны, то значение суммы аппроксимируется с нормальным распределением с 2p и .

Вычисление значение достаточно проблематично, поэтому в системе «DIEHARD» для p = 100 используется приближенное зна-

чение 12 . Таким образом, для каждой суммы можно вычислить значение

					Si	100
					Si	2
						2
					2 12
				erfс	2 12
	100


P-value X , , P-value Si ,		,	12				, i 1,100 .
P-value X , , P-value Si ,	2	,	12		2		, i 1,100 .
	2				2

Сто таких значение P-value для каждой подпоследовательности являются исходными данными для критерия Колмогорова– Смирнова, после чего полученная статистика для каждой из N подпоследовательностей снова обрабатывается при помощи критерия Колмогорова–Смирнова.

В программе «DIEAHARD» N принимается равным 10.

Длина тестируемой последовательности равна 10 2 100 1 4 =

= 7 960 байт.

Примечание. Повышение длины тестируемой последовательности возможно путем увеличения числа рассматриваемых подпоследовательностей N, что существенно снизит быстродействие теста.

2.11. Проверка на монотонность

Цель теста – проверить равномерность распределения чисел в исследуемой последовательности на основе анализа участков возрастания и убывания элементов последовательности.

Пусть = 1, 2,…, n – исходная последовательность m- разрядных чисел. Определим длины участков возрастания и убывания последовательности и вычислим Xi – число появлений участ-

ков длины i, i 1,6 . Х6 соответствует числу появлений участков с длиной, большей либо равной 6.

Пример 2.17

Вход:

ε= 1, 2, 9, 8, 5, 3, 6, 7, 0, 4.

Участки возрастания:

ε= | 1 2 9 | 8 | 5 | 3 6 7 | 0 4.

Сначала следует участок длиной 3 (1 2 9), затем два участка длиной 1 (8 и 5), затем участок длиной 3 (3 6 7) и участок длиной 2 (0 4). Таким образом, получаем

X1 = 2, X2 = 1, X3 = 2, X4 = 0, X5 = 0, X6 = 0.

Участки убывания:

ε = 1 | 2 | 9 8 5 3 | 6 | 7 0 | 4.

Сначала следуют два участка длиной 1 (1 и 2), затем следует участок длиной 4 (9 8 5 3), затем участок длиной 1 (6), затем участок длиной 2 (7 0) и снова участок длиной 1 (4).

Таким образом, получаем

X1 = 4, X2 = 1, X3 = 0, X4 = 1, X5 = 0, X6 = 0.

Полученные значения анализируются при помощи статистики:


					V			1		6	6 X		i	nb X		j	nb		j	a ,
					V						6 X			nb X			nb			a ,
															i					ij
								n 6 i 1 j 1
где aij , i				,	j				, и bi		, i				, – элементы матриц [12]:
где aij , i			1,6	,	j		1,6		, и bi		, i	1,6			, – элементы матриц [12]:
	4 529,4					9 044,9					13 568				18 091			22 615			27 892
		9 044,99				18 097					27 139				36 187			45 234			55 789
		9 044,99				18 097					27 139				36 187			45 234			55 789
A		13 568				27 139					40 721				54 281			67 852			83 685	,
A		18 091				36 187					54 281				72 414			90 470			111 580	,
		18 091				36 187					54 281				72 414			90 470			111 580
		22 615				45 234					67 852				90 470			113 262			139 476
		22 615				45 234					67 852				90 470			113 262			139 476
		27 892				55 789					83 685				111 580			139 476			172 860
		27 892				55 789					83 685				111 580			139 476			172 860

	1
	6
	6
			5
	24
	11

	120
B	120			.
		19
	720
	29
	29
	5040
	5040
		1
	840
	840

Данная статистика оценивается при помощи критерия 2 с шестью степенями свободы:

P-value , 2 obs P-value 6,V igamc 62 ,V2 .

Примечание. Критерий применяется с шестью, а не с пятью степенями свободы, так как длины интервалов не являются независи-

мыми. Модификация данного теста, использующая критерий 2 с

«правильным» числом степеней свободы, то есть с пятью, будет рассмотрена в главе 3, посвященной подборе тестов Д. Кнута.

В системе «DIEHARD» данный тест применяется со следующими параметрами: m = 32, числа рассматриваются нормированными (хотя для определения длин участков возрастания и убывания нормировать не обязательно – для нормированных и ненормированных чисел участки возрастания и убывания будут идентичны). Анализируются десять следующих друг за другом подпоследователностей длиной 10 000 чисел каждая, для каждой из них вычисляются значения P-value для участков возрастания и участков убывания, после чего к полученным значениям P-value применяется критерий Колмогорова–Смирнова. Затем операция повторяется и анализируется еще 10 следующих друг за другом подпоследовательностей.

Длина тестируемой последовательности равна 2 10 10 000 4 =

= 8 000 байт. Длину тестируемой области можно увеличить за счет увеличения числа прогонов теста.

2.12. Тест игры в кости

Цель теста – проверить равномерность распределения чисел в исследуемой последовательности на основе анализа взаимного расположения чисел последовательности.

Как и во многих других тестах «DIEHARD», основой для данного теста является задача из теории вероятностей, а именно: задача определения вероятности выигрыша при игре в кости. Кратко изложим основы этой игры. Имеется 2 кубика с гранями от 1 до 6. Кубики бросают одновременно, и определяется выпавшая сумма. В игре участвует несколько игроков, но в данной задаче анализируются только броски ведущего игрока (shooter). Возможно три исхода:

craps (сумма очков равна 2, 3 или 12) – ведущий игрок проигрывает;

natural (сумма очков равна 7 или 11) – ведущий игрок выигрывает;

point (все остальные случаи) – фиксируется выпавшее число и кубики снова бросаются до тех пор, пока снова не выпадет данное число (ведущий игрок выигрывает) или семерка (ведущий игрок проигрывает).

Теперь перейдем к тесту. Пусть = 1, 2,…, n – исходная последовательность m-разрядных чисел. Каждое число последовательности дает значение для одного кубика

1	6	i	, i		.
				1,n
		m
		2

Значение m должно быть больше либо равно log2 6 3, чтобы

обеспечить выпадение на кубике чисел от 1 до 6. Соответственно итог одного броска есть значение кубиков для двух чисел последовательности.

Пример 2.18

Вход:

ε = 1 15 9 8; m =4.

Первый бросок:
первый кубик (для числа 1): 1	6	1	1 0,375 1;
первый кубик (для числа 1): 1	6	24	1 0,375 1;
		24

второй кубик (для числа 15): 1 6 15 1 5,625 6 ;
			24
Результат первого броска: 1 + 6 =7.
Второй бросок:
первый кубик (для числа 9): 1	6		9	1 3,375 4 ;

			24
			24
второй кубик (для числа 8): 1	6		8	1 3 4 ;

		24
		24

Результат броска: 4 + 4 =8.

Ведущий игрок играет в кости 200 000 раз (одна игра подразумевает необходимое количество бросков кубиков до победы или поражения ведущего игрока).

Число побед ведущего игрока Win аппроксимируется с нормальным распределением со следующими параметрами:

200 000 p ,

200 000 p 1 p ,

где p 244495 . Рассчитывается значение

								244	, 200 000	244		244
P-value X , , P-value Win, 200 000									, 200 000		1
								495		495
								495		495		495
					244
			Win 200 000 495
	erfс		Win 200 000 495
	erfс
		2	200 000	244		244
		2	200 000	495	1	495
				495		495	.
			2				.
			2
	Также подсчитывается Yi – количество								игр с числом бросков,

равным i, i 1,21. Y21 соответствует количеству игр с числом бросков, большим или равным 21.

Вычисляется статистика

21	Y	200 000 p	s	2
χ2 obs	s		s		.
χ2 obs		200 000 ps			.
s 1		200 000 ps

которая анализируется при помощи критерия 2 числом степеней свободы, равным 20.

Соответствующие вероятности ps , s 1,21 (табл. 2.3) можно определить, используя следующую формулу [26]:

			1		,																s 1;
				3	,																s 1;
				3
								s 2			26 s 2					s 2
							27	s 2			26 s 2				25	s 2
				27					40					55
		ps					36				36				36					s
							36				36				36			,				2,20;

										648
										648
						20															s 21.
			1 pi																		s 21.
						i 1


Вычисляется значение																						2 obs
						2						2							20			2 obs
																					,
P-value , obs P-value 20, obs igamc																			2		,	2		.
																			2			2
Таблица 2.3. Вероятности											ps , s				, для теста игры в кости
Таблица 2.3. Вероятности											ps , s		1, 21		, для теста игры в кости
		s = 1				s = 2			s = 3		s = 4			s = 5			s = 6						s = 7

	0,3333				0,1883				0,1348		0,0966			0,0693			0,0497					0,0357

		s = 8				s = 9			s = 10		s = 11			s = 12			s = 13						s = 14

	0,0257				0,0185				0,0133		0,0096			0,0069			0,0050					0,0036

		s = 15			s = 16				s = 17		s = 18			s = 19			s = 20						s ≥ 21

	0,0026				0,0019				0,0014		0,0010			0,0007			0,0005					0,0016

Пример 2.19

Вход:

Значения бросков, соответствующие исследуемой последовательности:

4, 5, 12, 11, 6, 7, 11, 8, 10, 13, 15, 8, 2; m =4.

Тест: Win = 0;

Число игр Games = 0;

Первая игра: 4, 5, 12, 11, 6, 7, 11, 8, 10, 13, 15, 8, 2.

Games = 1;

Выпала 4. Ожидаем или 4 или 7. Пришла 7, следовательно, проигрыш. Число бросков = 6, увеличиваем Y6 на 1.

Вторая игра: 4, 5, 12, 11, 6, 7, 11, 8, 10, 13, 15, 8, 2.

Games = 2;

Выпала 11, следовательно, выигрыш. Win = 1. Число бросков = 1, увеличиваем Y1 на 1.

Третья игра: 4, 5, 12, 11, 6, 7, 11, 8, 10, 13, 15, 8, 2.

Games = 3;

Выпала 8. Ожидаем или 8 или 7. Пришла 8, следовательно, выигрыш.

Win = 2.Число бросков = 5, увеличиваем Y5 на 1.

Четвертая игра: 4, 5, 12, 11, 6, 7, 11, 8, 10, 13, 15, 8, 2.

Games = 4;

Выпала 2, следовательно, проигрыш. Число бросков = 1, увеличиваем Y1 на 1.

Таким образом, рассматриваемая последовательность представляет собой набор из четырех игр, две из которых состояли из одного броска, одна – из пяти бросков и одна – из шести. Две игры завершились победой.

В программе «DIEHARD» данный тест применяется к последовательности 32-разрядных чисел (m = 32).

2.13. Тест гориллы

Цель теста – проверить равномерность распределения чисел в исследуемой последовательности на основе анализа отсутствующих в ней подпоследовательностей.

Тест гориллы – усиленный вариант обезьяньих тестов.

Пусть = 1, 2,…, n – последовательность m-разрядных чисел.

Преобразуем ее в битовые строки i ,		i		длиной	2m* m* 1 ,
			1,m
m* m . Каждый бит новой строки ij		есть i-й бит в j-м числе ис-
ходной последовательности, j	1, 2m*	m* 1		.

Примечание. Для выполнения теста длина исходной последовательности должна удовлетворять следующему неравенству:

n 2m* m* 1 .

Каждая строка i представляется в виде 2m* пересекающихся

m* -разрядных слов. Число отсутствующих слов Xi в каждой строке аппроксимируется с нормальным распределением со средним

2m* e	2m*	2m	*
	2m*
		e

и отклонением , следовательно, можно рассчитать значения

										2m*
							S	i
							S			e
										e
						erfс
						erfс			2
			2	m*
P-value X , , P-value X		,	2		,						,
P-value X , , P-value X		,		e	,			2			,
	i			e				2

а затем проанализировать их при помощи критерия Колмогорова– Смирнова.

Пример 2.20

Вход:

ε = 15 4 9 5 7 1 8 3 2 0; n = 10;

m = 4; m* 3 .

Тест:

2m* m* 1 23 3 1 10 n

ε = 1111 0100 1001 0101 0111 0001 1000 0011 0010 0000.

Формирование последовательностей:

1 :

ε = 1111 0100 1001 0101 0111 0001 1000 0011 0010 0000;

1 = 1010001000.

Слова: {101}, {010}, {100}, {000}, {001}, {010}, {100}, {000}.

Число отсутствующих слов – 2: {011} и {111}.

2 :

ε= 1111 0100 1001 0101 0111 0001 1000 0011 0010 0000;

2 = 1101100000.

Слова: {110}, {101}, {011}, {110}, {100}, {000}, {000}, {000}.

Число отсутствующих слов – 3: {001}, {010}, {111}.

3 :

ε= 1111 0100 1001 0101 0111 0001 1000 0011 0010 0000;

3 = 1000100110.

Слова: {100}, {000}, {001}, {010}, {100}, {001}, {011}, {110}.

Число отсутствующих слов – 2: {101} и {111}.

4 :

ε= 1111 0100 1001 0101 0111 0001 1000 0011 0010 0000;

4 = 1011110100.

Слова: {101}, {011}, {111}, {111}, {110}, {101}, {010}, {100}.

Число отсутствующих слов – 2: {000} и {001}.

В системе «DIEHARD» используются следующие параметры: m 32 , m* 26 . Таким образом,

2m*	2	26	24 687 971.
e	e

Вычисление математически сложно, поэтому в системе используется приближенное значение

4 170 .

Таким образом, формула для расчета значений P-value принимает вид:

P-value X , , P-value Xi , 24 687 971, 4170

		S	i	24	687 971
	erfс		i
	erfс
				2	4170
				2	4170	.
				2		.
				2
Длина тестируемой					последовательности равна (226 25) 4

= 268 435 556 байт.

Примечание. Данный тест действительно будет трудно обмануть, однако плата за стойкость – значительное время обработки по сравнению с другими тестами. Время обработки можно снизить

путем уменьшения m* , однако в данном случае придется рассчитывать или экспериментально определять значение , что также является сложной вычислительной задачей.

2.14. Тест НОД

Цель теста – проверить равномерность распределения чисел в исследуемой последовательности на основе взаимного расположения элементов последовательности.

Пусть = 1, 2,…, n – последовательность m-разрядных чисел. Два соседних числа образуют исходные данные для нахождения НОД и определения числа итераций k в алгоритме Евклида [12].

Пример 2.21

Вход:

ε = 297 366 255 420.

Тест:

Вычисляем НОД 297, 366

k Вычисления

1366 = 1·297 + 69

2297 = 4·69 + 21

3	69	= 3·21	+ 6
4	21	= 3·6	+ 3
5	6	= 2·3	+ 0

НОД = 3, число итераций алгоритма Евклида = 5.

Вычисляем НОД 255, 420

k Вычисления

1420 = 1·255 + 165

2255 = 1·165 + 90

3165 = 1·90 + 75

4	90	= 1·75	+ 15
5	75	= 5·15	+ 0

НОД = 15, число итераций алгоритма Евклида = 5.

Подсчитывается YsНОД , s 1,101, – число пар чисел, имеющих НОД, равный s (в Y101НОД записывается число пар, имеющих НОД,

равный или больший 101) и применяется критерий 2 со 100 степенями свободы

НОД

101

χНОД2 obs

НОД

s 1

psНОД ,

Для расчета вероятностей

(табл. 2.4), применя-

1,101

ется следующая формула [12, 29]:

s 1,100;

psНОД

100

piНОД,

s 101.

i 1

Значение 2 obs оценивается при помощи значения

P-value ,χ2 obs P-value 100,χНОД2

obs

igamc

100 ,

χНОД obs

Примечание. В системе «DIEHARD» данный тест применяется к 32-разрядным числам, отсюда такое большое число s. Для последовательностей с числами меньшей разрядности можно уменьшить число s для увеличения быстродействия теста.

Таблица 2.4. Значения вероятностей psНОД , s 1,101 для теста НОД

s = 1	s = 2	s = 3	s = 4	s = 5	s = 6	s = 7	s = 8	s = 9	s = 10
0,6079	0,1520	0,0675	0,0380	0,0243	0,0169	0,0124	0,0095	0,0075	0,0061
s = 11	s = 12	s = 13	s = 14	s = 15	s = 16	s = 17	s = 18	s = 19	s = 20
0,0050	0,0042	0,0036	0,0031	0,0027	0,0024	0,0021	0,0019	0,0017	0,0015
s = 21	s = 22	s = 23	s = 24	s = 25	s = 26	s = 27	s = 28	s = 29	s = 30
0,0014	0,0013	0,0011	0,0011	0,0010	0,0009	0,0008	0,0008	0,0007	0,0007
s = 31	s = 32	s = 33	s = 34	s = 35	s = 36	s = 37	s = 38	s = 39	s = 40
0,0006	0,0006	0,0006	0,0005	0,0005	0,0005	0,0004	0,0004	0,0004	0,0004
s = 41	s = 42	s = 43	s = 44	s = 45	s = 46	s = 47	s = 48	s = 49	s = 50
0,0004	0,0003	0,0003	0,0003	0,0003	0,0003	0,0003	0,0003	0,0003	0,0002
s = 51	s = 52	s = 53	s = 54	s = 55	s = 56	s = 57	s = 58	s = 59	s = 60
0,0002	0,0002	0,0002	0,0002	0,0002	0,0002	0,0002	0,0002	0,0002	0,0002
s = 61	s = 62	s = 63	s = 64	s = 65	s = 66	s = 67	s = 68	s = 69	s = 70
0,0002	0,0002	0,0002	0,0001	0,0001	0,0001	0,0001	0,0001	0,0001	0,0001
s = 71	s = 72	s = 73	s = 74	s = 75	s = 76	s = 77	s = 78	s = 79	s = 80
0,0001	0,0001	0,0001	0,0001	0,0001	0,0001	0,0001	0,0001	0,0001	0,0001
s = 81	s = 82	s = 83	s = 84	s = 85	s = 86	s = 87	s = 88	s = 89	s = 90
0,0001	0,0001	0,0001	0,0001	0,0001	0,0001	0,0001	0,0001	0,0001	0,0001
s = 91	s = 92	s = 93	s = 94	s = 95	s = 96	s = 97	s = 98	s = 99	s = 100
0,0001	0,0001	0,0001	0,0001	0,0001	0,0001	0,0001	0,0001	0,0001	0,0001
s = 101
0,0060

Также подсчитывается Ysk , s 3, 36 , – число пар чисел, при нахождении НОД которых алгоритм Евклида совершил k итераций (в Y3k записывается число пар, при нахождении НОД которых алгоритм Евклида совершил число итераций, меньшее либо равное 3, в Y36k записывается число пар, при нахождении НОД которых алгоритм Евклида совершил число итераций, большее либо равное 36). В [29] показано, что Ysk ассимптотически нормально распределены со средним

0,842766 ln n 0,06535

и отклонением

0,5151ln n 0,1666 .

Расчет среднего

Y k Ysk s 3

иоценка полученного значения

P-value X , ,

	k	n		n
P-value Y		, 0,842766 ln		0,06535, 0,5151ln		0,1666

			2		2

		k			n
	Y		0,842766 ln					0,06535
	Y		0,842766 ln			2		0,06535
erfс						2
erfс				n
				n
			2	0,5151ln			0,1666
			2	0,5151ln	2		0,1666
					2
				2
				2

сделает тест менее сильным, поэтому в системе «DIEHARD» реа-

лизована оценка каждого значения Y k ,						s	3, 36	. В [29] показано,
					s
что Y k	с заданными	и можно аппроксимировать с биноми-
s
альным распределением со следующими вероятностями:
	50			j		50 j
	50			j		50 j
					0,524		, s 1,50 .
	P s j	j	0,376		0,524		, s 1,50 .
		j

Теперь можно применить критерий 2										со 100 степенями свобо-
ды
					k		n		k 2
36			Y					p	s
			Y					p
				s			2			,
χk2 obs						n	2	k		,
		s 3				n		k
							ps
						2	ps
						2
где вероятности psk , s		(табл. 2.5),								рассчитываются по сле-
где вероятности psk , s	3, 36	(табл. 2.5),								рассчитываются по сле-
дующей формуле:
			81

s 3;

0,376 j 0,52450 j ,

j 1

0,524

s 4,35;

0,376

pkj

s 36.

j 3

Значение 2 obs оценивается при помощи значения
				32 χ2			obs
	2	2				k
P-value ,χ		obs P-value 32,χk	obs igamc	2	,		2	.
				2			2

Примечание. Тест можно значительно усилить, если для числа итераций k рассматривать не 33 категории, а все возможные. В [12] показано, что в наихудшем случае число итераций k не превышает величины

4,8 log10 2m 0,32 .

Для системы «DIEHARD» значение m 32 , соответственно k 4,8 log10 232 0,32 46 .

Таблица 2.5. Значения вероятностей psk , s 3, 36 для теста НОД

	s = 3		s = 4		s = 5	s = 6		s = 7
0,000000274		0,000001744		0,000009668		0,000043691	0,000165482
	s = 8		s = 9		s = 10			s = 12
	s = 8		s = 9		s = 10	s = 11		s = 12
0,000535959		0,001507099		0,003723307		0,008158294	0,015976660
	s = 13		s = 14		s = 15	s = 16		s = 17
0,028140349		0,044813249		0,064806852		0,085422493	0,102945056
	s = 18		s = 19		s = 20	s = 21		s = 22
0,113723491		0,115411694		0,107791563		0,092787609	0,073700181
	s = 23		s = 24		s = 25			s = 27
	s = 23		s = 24		s = 25	s = 26		s = 27
0,054063232		0,036648633		0,022966477		0,013306514	0,007127136
	s = 28		s = 29		s = 30	s = 31		s = 32
0,003527671		0,001612561		0,000680170		0,000264417	0,000094601
	s = 33		s = 34		s = 35	s = 36
0,000031093		0,000009368		0,000002580		0,000000833
				82

Программная реализация теста анализирует 1 000 000 пар чисел, соответственно, длина последовательности равна 2 · 1000 000 · 4 = = 8 000 000 байт. Существует усиленный вариант данного теста, анализирующий 10 000 000 пар чисел, длина последовательности для усиленного варианта составляет 80 000 000 байт.

Рассмотренные тесты показывают силу системы «DIEHARD». Действительно, сложно сформировать заведомо плохую последовательность, не удовлетворяющую совокупности требований на случайность, но успешно проходящую все тесты системы. Однако системе присущи и недостатки.

Жестко заданный размер области тестирования. Как можно заметить из описания тестов, размер области тестирования значительно отличается для разных тестов. Например, тест дней рождений анализирует всего 2 000 байт, в то время как для реализации теста гориллы необходимо 268 435 556 байт. Увеличить значение области тестирования до максимального значения среди всех тестов не представляется возможным, так как большинство тестов использует или приближенные или экспериментальные значения для оценки ожидаемых величин, причем эти значения жестко привязаны к размеру области тестирования. Оценивать же качество последовательности на основе свойств части категорически неправильно – последовательность может иметь предпериод и в область тестирования может попасть именно он.

Отбрасывание чисел при разбиении на подпоследовательности.

Ряд тестов разбивает исходную последовательность на подпоследовательности, отбрасывая при этом неиспользуемые элементы последовательности. В ряде случаев число отбрасываемых элементов может быть критично для некоторых приложений. Предположим, пользователь сформировал последовательность длиной 1000 чисел, при этом первые 900 элементов по своим свойствам неотличимы от истинно случайной последовательности, а последние 100 в силу каких-нибудь причин равны 0. Алгоритма теста использует 900 чисел, отбрасывая при этом 100 чисел. Статистика теста показывает положительный результат прохождения, пользователь считает, что вся последовательность случайна и использует ее, к примеру, для формирования паролей, состоящих из 20 чисел. Первые

900 чисел сформируют 45 случайных паролей, а последние числа дадут мало того, что нулевые, так еще и одинаковые пароли. Естественно, в качественных системах генерации паролей повторение будет обнаружено, однако факт непроверки части последовательности следует иметь в виду. При этом система «DIEHARD» не отображает, сколько чисел из анализируемой последовательности обрабатывается конкретным тестом.

Использование экспериментальных или приближенных зна-

чений. Большинство тестов «DIEHARD» использует для вычисления статистик экспериментальные или приближенные значения. Недостаток данного подхода проиллюстрируем следующей ситуацией. Предположим, результаты испытаний можно разделить на две категории. Для ожидаемых значений к каждой категории, полученных при помощи точных вычислений, значение статистики теста

Т2 obs 6,64 .

Соответствующее значение P-value есть

P-value , χ2 obs P-value 2 1; 6,64

2 1			6,64		.
igamc		,		0,00997 0,01
igamc	2	,	2	0,00997 0,01
	2		2

Для уровня значимости 0,01 тест считается не пройденным.

Теперь предположим, что при расчете ожидаемых значений использовались приближенные методы, и значение статистики теста получилось равным

Э2 obs 6,63 .

Соответствующее значение P-value есть

P-value ,χ2 obs P-value 2 1; 6,63

2	1		6,63
igamc		,		0,010028 0,01.
	2		2

Для уровня значимости 0,01 тест считается пройденным.

Таким образом, последовательность, которая на самом деле является неслучайной, тестом будет трактоваться как случайная.

Двоякость в трактовке значений P-value для разных критериев.

Как уже упоминалось ранее, при оценке результатов критерий 2 в

системе «DIEHARD» формирует отличное от оригинального P- value значение

2			2 obs
		,
P-valueDIEHARD 1 P-value , obs 1 igamc	2	,	2	.
	2		2

Последующее использование критерия Колмогорова–Смирнова, а точнее, Андерсона–Дарлинга, нейтрализует это различие, правда, только в том случае, если все анализируемые критерием Колмого- рова–Смирнова значения P-value больше либо равны уровня значимости теста. При этом, данное свойство с некоторыми оговорками будет действовать только для малых уровней значимости (например, 0.01), так как с точки зрения Д. Кнута вероятность появления слишком случайных [12] событий, т.е. испытаний с P-value 1 , меньше, чем . Кроме того, критерий Колмого-

рова–Смирнова при единичных случаях появления слишком случайных событий их попросту отсеет. Правда, истинная случайная последовательность в такой реализации тест не пройдет. В связи с

этим, если P-valueDIEHARD для критерия Колмогорова–Смирнова показывает, что последовательность тест не прошла, необходимо проверить значения характеристик, участвовавших в вычислении данной величины.

Отсутствие интегральной оценки результатов испытаний.

Каждый тест формирует отчет в виде текстового файла с указанием имени тестируемого файла и полученного значения P-value. Учитывая, что разные тесты анализируют различные участки последовательности, используют как точные, так и приближенные значения, а также двойственность в трактовке значений P-value, простое сравнение полученных значений P-value с уровнем значимости, а также применение к ним критериев Колмогорова–Смирнова или Андерсона–Дарлинга не даст полного представления о свойствах исследуемой последовательности. Хорошим решением явилось бы введение некоей интегральной оценки, основанной на таких аргументах, как длина исследуемой последовательности, область тестирования, точность или приближенность расчетов ожидаемых значений и т.п.

Указанные недостатки ни в коей мере не умаляют достоинств самих тестов «DIEHARD». Следует также помнить, что сама система была реализована более 15 лет назад, соответственно ряд программистских и вычислительных решений был попросту не доступен в то время. При этом сама системе ничуть не утратила своей актуальности и по сей день используется как одно из основных средств при оценке свойств псевдослучайных последовательностей.

ГЛАВА 3. ПОДБОРКА ТЕСТОВ Д. КНУТА

В состав данной подборки [11] включены следующие тесты, которые традиционно применяются для проверки статистических свойств последовательностей:

проверка равномерности (frequency test);

проверка серий (serial test);

проверка интервалов (gap test);

покер-тест (poker test);

тест собирателя купонов (coupon collector’s);

проверка перестановок (permutation test);

проверка на монотонность (runs test);

тест «максимум-t» (maximum of t test);

проверка конфликтов (collision test);

тест дней рождений (birthday spacing’s test);

проверка корреляции (serial correlation test).

3.1.Проверка равномерности

Первый тест, с которого, по мнению Д. Кнута, следует начать

исследование последовательности. Пусть = 1, 2,…, n – последовательность m-разрядных чисел. Если последовательность случайна, то все числа должны быть равновероятны. Проверить это можно двумя способами.

Первый способ состоит в применении критерия 2 . Пусть Ys – количество появлений чисел, равных s, s 0, 2m 1 . Вероятность появления любого числа равняется 21m , соответственно статистика теста

			1		2
2m 1	Ys n
			2	m
2 obs						.
	n	2m
s 0		1

Полученное значение оценивается при помощи критерия 2 с2m 1 степенями свободы. Вычисляется значение

P-value , 2 obs P-value 2m 1, 2 obs igamc	2m 1	,	2 obs	.
P-value , 2 obs P-value 2m 1, 2 obs igamc		,		.
	2		2

Пример 3.1

Вход:

= 3 2 6 7 0 1 5 2 7 3; n = 10;

m = 3.

Тест:

Вероятность появления любого числа равна 213 18 .

Y0 = 1;

Y1 = 1;

Y2 = 2;

Y3 = 2;

Y4 = 0;

Y5 = 1;

Y6 = 1;

Y7 = 2.

							10			1		2				10		1		2			2	10			1		2				2	10			1	2
					1		10			8					1	10		8					2	10			8						2	10			8
2 obs										8								8									8										8
2 obs							10		1							10	1							10		1								10		1
							10		1							10	1							10		1								10		1
									8								8									8										8
		10		1			2				10			1		2			10			1		2				10			1		2
	0	10		8				1			10			8		1			10			8			2			10			8
				8										8								8									8				2,8
		10	1									10	1							10	1								10 1						2,8
			8										8								8									8
						2																				7			2,8
P-value ,							obs P-value 7; 2,8 igamc																				,					0,902867 .
P-value ,							obs P-value 7; 2,8 igamc																			2	,		2			0,902867 .
																										2			2

Второй способ состоит в нормировании исходной последовательности

норм 2m1 , 2m2 , ..., 2mn

и применении к числам последовательности норм критерия Колмо- горова–Смирнова или Андерсона–Дарлинга с F x x .

Пример 3.2

Вход:

= 3, 2, 6, 7, 0, 1, 5, 2, 7, 3; n = 10;

m = 3.

Тест:

норм 233 , 223 , 263 , 273 , 203 , 213 , 253 , 223 , 273 , 233 0,375; 0,25; 0,75;

0,875; 0; 0,125; 0,625; 0,25; 0,875; 0,375.

Упорядочим элементы последовательности в порядке возрастания

*норм 0; 0,125; 0,25; 0,25; 0,375; 0,375; 0,625; 0,75; 0,875; 0,875.

Применим критерий Колмогорова–Смирнова
					1			2					3			4		5
	К10		10 max			0;				0,125;				0,25;			0,25;		0,375;
	К10		10 max		10	0;		10		0,125;		10		0,25;		10	0,25;	10	0,375;
					10			10				10				10		10
6		0,375;		7	0,625;			8	0,75;		9		0,875;		10		0,875

10				10			10				10				10
10				10			10				10				10

10 max 0,1; 0,075; 0,05; 0,15; 0,125; 0,225; 0,075; 0,05; 0,025; 0,125

10 0,225 0,71.

P-value K10 0,34 .
			0		1		2		3		4
К10	10 max	0		; 0,125		; 0,25		; 0,25		; 0,375		;
			10		10		10		10		10

0,375	5	; 0,625	6	; 0,75	7	, 0,875	8	; 0,875	9

	10		10		10		10		10

10 max 0; 0,025; 0,05; 0,05; 0,025; 0,125; 0,025; 0,05; 0,075; 0,025 10 0,075 0,31.

P-value K10 0,89 .

3.2. Проверка серий

Цель теста – исследовать последовательность на случайность, анализируя длины несцепленных серий различной длины.

Пусть = 1, 2,…, n – двоичная последовательность длины n и m – длина серии. Подсчитывается число появлений νi1...im всевоз-

можных непересекающихся серий длиной m (лишние биты отбрасываются) и вычисляется статистика

χ2 obs

νi1...im

		n			1		2
ν
ν	i1...im
	i1...im				2	m			1
		m			2				1
	n		1					n		1

			2	m						2	m
	m		2					m		2

νi

...i

νi

...i

Полученный результат анализируется при помощи критерия 2 с числом степеней свободы, равным 2m – 1. Вычисляется значение

P-value , 2 obs P-value 2m 1, 2 obs igamc	2m 1	,	2 obs	.
P-value , 2 obs P-value 2m 1, 2 obs igamc		,		.
	2		2

Примечание. Проверка равномерности есть частный случай проверки серий при разрядности числа, равной размеру серии.

Пример 3.3

Вход:

= 11001001000011111101101010100010001000010110100011; n = 50;

m = 3.

Тест:

Разделим последовательность на серии-тройки, отбрасывая последние два бита (11) как не принадлежащие ни одной тройке

* = 110 010 010 000 111 111 011 010 101 000 100 010 000 101 101 000;

000 = 4; 001 = 0; 010 = 4; 011 = 1; 100 = 1; 101 = 3; 110 = 1; 111 = 2.

n	1		50		1			1	2 .
							16
	2	m		3	2	3		8
m

χ2 obs 12 4 2 2 0 2 2 4 2 2 1 2 2 1 2 2 3 2 2

1 2 2 2 2 2 8 .

P-value , 2 obs P-value 7, 8 igamc 72 , 82 0,332594 .

3.3. Проверка интервалов

Данный тест проверяет равномерность распределения символов в исследуемой последовательности, анализируя длины промежутков между элементами последовательности, принадлежащих определенному числовому интервалу.

Пусть = 1, 2,…, n – последовательность m-разрядных чисел. Пусть и два целых числа, таких, что 0 < < 2m. Подсчитываются длины интервалов между числами, лежащими в промежутке [ ; ). После этого определяется число интервалов i,

0, t

, длины i

(в t записывается число интервалов, имеющих

длину, большую или равную t) и рассчитывается статистика

η p

χ2 obs

i 0

η pi

где η νi

– общее число интервалов, а вероятности определяют-

i 0

ся следующим образом:

β α

β α i

i 0, t 1 ;

β α

i t.

Значение t выбирается таким образом, чтобы каждое значениеi, i 0, t , было больше либо равно 5.

Полученный результат анализируется при помощи критерия 2 с числом степеней свободы, равным t. Вычисляется значение

P-value , 2 obs P-value t, 2 obs igamc	t	,	2 obs	.

2			2

Пример 3.4

Вход:

= 0 5 4 1 0 4 6 1; m = 3;

= 0;= 2.

Тест:

Начинаем анализировать последовательность. Находим первое число, лежащее в интервале [0; 2). Это 0 – первый элемент последовательности. Следующее число, лежащее в заданном интервале, 1, четвертый элемент последовательности, отделяет от 0 два элемента последовательности – 5 и 4. Таким образом, найден первый интервал длиной 2: {0-5-4-1}. Продолжая, получаем

0 = 1: {1-0},

1 = 0,

2 = 2: {0-5-4-1}, {0-4-6-1}, t = 2.

= 2 + 0 + 2 = 4.

p0 2230 1 2230 0 0,25 ;

p1	2	0			2		0 1	0,1875;
				1
	23			1		23
	23					23
p			2 0 2
	1					0,5625 .
	1	23				0,5625 .
1		23

χ2 obs	1 4 0,25 2			0 4 0,1875 2	2 4 0,5625 2					0,78 .
χ2 obs				4 0,1875	4 0,5625					0,78 .
			4 0,25	4 0,1875	4 0,5625
		2				2		0,78
P-value ,			obs P-value 2, 0,78 igamc				,		0,677057 .
P-value ,			obs P-value 2, 0,78 igamc			2	,	2	0,677057 .
						2		2

3.4. Покер-тест

Данный тест проверяет равномерность распределения символов в исследуемой последовательности, анализируя различные комбинации чисел в подпоследовательностях.

Пусть = 1, 2,…, n – последовательность m-разрядных чисел

длины n. Разобьем ее на подпоследовательности длиной t каждая (лишние биты отбрасываются). Подсчитывается число подпоследо-

вательностей νi , i 1, t , содержащих i различных чисел, и вычисляется статистика

				n		2
r	ν	i				p
	ν					p
						i
χ2 obs				t		,
i 1			n		p
					p
						i
			t

где pi	d d 1 ... d i 1 t		,	d 2	m	1.
		i
	d t

Полученный результат анализируется при помощи критерия2 с числом степеней свободы, равным t – 1. Вычисляется значение

P-value , 2 obs P-value t 1, 2 obs igamc	t 1	,	2 obs	.

2			2

Пример 3.5

Вход:

= 0 1 5 0 1 3 2 2 2 3 0 1 0 2 3 5 1 2 3 4 0 3 3 3 5 1 2; n = 27;

t = 5.

Тест:

Разбиваем последовательность на группы по 5 чисел, отбрасывая 1 и 2 как не принадлежащие ни одной группе

* = 0 1 5 0 1 3 2 2 2 3 0 1 0 2 3 5 1 2 3 4 0 3 3 3 5,

1 = 0,2 = 1: {3 2 2 2 3},

3 = 2: {0 1 5 0 1} и {0 3 3 3 5},4 = 1: {0 1 0 2 3},

5 = 1: {5 1 2 3 4}. d = 23 1 = 7,

p1	7	5	0,0004 ,
	7
	75
	75	1

p2		7 6	5				0,037 ,
p2		7 6					0,037 ,
		75	2
p3		7 6		5	5
p3		7 6		5	0,31,
		75				3

p4		7 6					5
p4		7 6		5 4 0,5 ,
		75					4
p5		7 6						5
p5		7 6		5 4 3 0,15 .
			75					4
n		27			5.


t		5							1 5 0,037 2	2 5 0,31 2
2 obs				0 5 0,0004 2					1 5 0,037 2	2 5 0,31 2
2 obs						5 0,0004			5 0,037
						5 0,0004			5 0,037		5 0,31
	1 5 0,5 2							1 5 0,15 2	6,87.
									6,87.
		5 0,5						5 0,15
					2						4		6,87
P-value ,						obs P-value 4; 6,87 igamc						,		0,142920.
P-value ,						obs P-value 4; 6,87 igamc					2	,	2	0,142920.
											2		2

3.5. Тест собирателя купонов

Пусть = 1, 2,…, n – последовательность m-разрядных чисел длины n. Подсчитывается число r подпоследовательностей длины

r, r 2m , t , (в t записывается число подпоследовательностей с

длиной, большей либо равной t) содержащих полный набор чисел от 0 до 2m – 1 и вычисляется критерий

				t			2
							pi
	t	νi			νj		pi
	t		j d
χ2 obs								,
χ2 obs				t				,
	i d			t
						pi
			νj			pi
		j d
		94

где

p		d!	r 1 , r
		d!				d, t 1 ,
						d, t 1 ,
	r	d r d 1

		pt 1		d!	t 1		,

				d t 1
				d t 1	d

d 2m . Значение t выбирается таким образом, чтобы каждое значение i , i d, t , было больше либо равно 5.

Полученный результат анализируется при помощи критерия 2 с числом степеней свободы, равным t 2m . Вычисляется значение

P-value , 2 obs P-value t 2m , 2 obs igamc	t 2m	,	2 obs	.

2			2

Примечание. Последний собираемый набор может оказаться неполным ввиду завершения последовательности и не будет учитываться при расчете статистики теста. При больших значениях m данный фрагмент может оказаться значительным, данный факт следует учитывать при формировании заключения о свойствах тестируемой последовательности.

Пример 3.6

Вход:

= 0 1 2 0 1 3 2 2 2 3 0 1 0 2 3 1 1 1 0 3 2 1 2; m = 2.

Тест:

Начинаем с первого элемента последовательности. Длина первой

подпоследовательности, содержащей все числа от 0 до 2m 1, равна 6: {0 1 2 0 1 3}. Продолжая, получаем

4 = 1 {0 2 3 1},5 = 1 {1 1 0 3 2},

6 = 2 {0 1 2 0 1 3} и {2 2 2 3 0 1}. t = 6.

νj 1 1 2 4 ,

j 4

d = 22 = 4;

p4		4!	4 1				0,09 ,

		44		4
					1

p5		4!	5		1		0,14 ,

		45		4
					1

p6				4!		6 1
	1						0,77 ,
			46 1
							4


χ2 obs (1 4 0,09)2			(1 4 0,14)2	(2 4 0,77)2			1,87 .
χ2 obs (1 4 0,09)2			4 0,14	4 0,77			1,87 .
		4 0,09	4 0,14	4 0,77
	2			4		1,87
P-value ,		obs P-value 4; 1,87 igamc			,	2	0,759654.
P-value ,		obs P-value 4; 1,87 igamc			,		0,759654.
				2

3.6. Проверка перестановок

Данный тест проверяет равномерность распределения символов в исследуемой последовательности, анализируя взаимное расположение чисел в подпоследовательностях.

Пусть = 1, 2,…, n – последовательность m-разрядных чисел длины n. Разобьем ее на подпоследовательности длиной t чисел каждая (лишние биты отбрасываются). В каждой такой подпоследовательности возможно t! вариантов относительного расположения чисел. Подсчитывается, сколько раз встречается каждое такое

расположение i , i 1, t! и вычисляется статистика:

χ2 obs

i 1

1 i 1

Полученный результат анализируется при помощи критерия 2 с числом степеней свободы, равным t! – 1. Вычисляется значение

P-value , 2 obs P-value t! 1, 2 obs igamc	t! 1	,	2 obs	.

2			2

Пример 3.7

Вход:

= 3 5 4 2 1 4 0 1 0; n = 9;

t = 2.

Тест:

Разбиваем исходную последовательность на пары, последний 0 отбрасываем как не относящийся ни к одной из пар.

* = {3 5} {4 2} {1 4} {0 1},

1 (первое число меньше второго) = 3: {3 5}, {1 4}, {0 1};2 (первое число больше второго) = 1: {4 2}.

									2					2
χ2 obs			1			9		1			9		1
			1		3	9		1		1	9		1		1.
					3					1					1.
	9			1			2	2!				2	2!
	9			1			2	2!				2	2!

		2		2!
		2		2!

P-value , 2 obs P-value 1, 1 igamc 12 , 12 0,317311.

3.7. Проверка на монотонность

Данный тест проверяет равномерность распределения символов в исследуемой последовательности, анализируя участки невозрастания и неубывания элементов последовательности.

Пусть = 1, 2,…, n – последовательность m-разрядных чисел. Пусть νi , i 1, t , – число участков невозрастания (неубывания) длиной i (в νt записывается число участков с длиной, большей либо равной t). Значение t выбирается таким образом, чтобы каждое значение i , i 1, t , было больше либо равно 5.

Вычисляется статистика

			t			2
						pi
t	νi			νj		pi
t		j 1
χ2 obs							,
χ2 obs		t					,
i 1		t
					pi
		νj			pi
	j 1
	97

где

1				1
1				1	,	i 1, t 1 ;

			i	1 !
i!			i	1 !
pi		t 1
1	p j ,					i t.
		j 1
		j 1

Полученный результат анализируется при помощи критерия 2 с числом степеней свободы, равным t – 1.

Вычисляется значение

P-value ,	2	obs P-value t 1,	2	obs igamc	t 1		,	2 obs	.
						2		2

Примечание. Отличие от теста монотонности системы «DIEHARD» заключается в том, что после нахождения участка невозрастания (неубывания) очередной участок начинает искаться не со следующего элемента, а с элемента, следующего за следующим.

Пример 3.8

Вход:

= 3 5 4 2 1 4 6 1 0.

Тест:

Участки невозрастания:

= 3 5 4 2 1 4 6 1 0.

Берем первый элемент последовательности, это 3. Следующий за ней элемент – 5 – больше, чем 3, следовательно, участок невозрастания состоит из одного элемента: {3}. Пропускаем следующий за участком элемент, то есть 5, и начинаем дальнейший анализ с 2. Продолжая, получаем

1 = 1: {3},

2 = 0,3 = 2: {4 2 1} и {6 1 0} ,

νj ν1 ν2 ν3 3 ,

j 1

p1 11 21! 12 , p2 21! 31! 13 ,

p 1 1		1	1 ,
3	2	3		6
	2	3		6		2					2					2
					1	2	0	3		1	2	2	3		1	2
		1 3			2		0	3		3		2	3		6
2 obs					2					3					6		5,67 .
			3	1				3	1				3	1
				2					3					6

P-value ,	2	obs P-value 2; 5,67		2		5,67
			igamc		,		0,058719.
				2		2

Участки неубывания:

= 3 5 4 2 1 4 6 1 0,

1 = 2: {2} и {0},2 = 2: {3 5} и {4 6},

j 1 2 4 ,

j 1

Число категорий для участков невозрастания и неубывания могут не совпадать. Это связано с тем, что после нахождения очередного участка следующий за ним элемент последовательности не рассматривается, соответственно проверки невозрастания и неубывания являются независимыми друг от друга.

p 1			1		1 ,
p 1					1 ,
1	1	2!				2
	1	2!				2
p2 1		1				1 .
p2 1		2!				1 .
		2!				2
						4		1	2	2	4		1	2
				2		4		2		2	4		2
2 obs								2					2		0.
2 obs						4	1				4	1			0.
						4	1				4	1
							2					2

P-value , 2 obs P-value 1, 0 igamc 12 , 02 1.

3.8. Тест «максимум-t»

Данный тест проверяет равномерность распределения символов в исследуемой последовательности, анализируя распределение чисел по подпоследовательностям.

Пусть = 1, 2,…, n – последовательность m-разрядных чисел. Преобразуем ее в нормированную последовательность

норм 2m1 , 2m2 , ..., 2mn .

Разобьем нормированную последовательность на	n	непере-

t

секающихся подпоследовательностей длиной t и определим максимальный элемент в каждой подпоследовательности

t j 1 1

t j

1 t

m ,

m ,...,

j 1, .

Vj max

Полученные значения Vj анализируются при помощи критерия

Колмогорова–Смирнова или Андерсона–Дарлинга с F x xt .

Примечание. Выражение для функции распределения получается следующим образом. Пусть U1, U2, … , Ut – некие нормированные значения. Тогда

P max U1,U2 ,...,Ut x P U1 x P U2 x ... P Ut x x xt

i 1

Пример 3.9

Вход:

= 3 2 6 7 0 1 5 2 4 3; n = 10;

m = 3; t = 3.

Тест:

Для простоты реализации теста можно нормировать только максимальные элементы. Поэтому сначала разобьем последовательность на подпоследовательности длиной 3. Последний элемент последовательности (3) отбрасываем, как не относящийся ни к одной подпоследовательности.

* = {3 2 6} {7 0 1} {5 2 4};

100

Для первой подпоследовательности максимальный элемент будет 6, для второй – 7, для третьей – 5. Соответственно нормированные максимальные элементы будут

V1 263 0,75 ;

V2 273 0,875;

V1 253 0,625 .

Упорядочим значения в порядке возрастания: 0,625; 0,75; 0,875.

Применим критерий Колмогорова–Смирнова

			1				3		2					3			3			3
К3		3 max		0,625				;		0,75					;			0,875
К3		3 max	3	0,625				;	3	0,75					;		3	0,875
			3						3								3
	3 max 0,089; 0,245; 0,33											3 0,33 0,577.
P-value K3 0,49 .
					3	0					3		1						3	2
К3		3 max	0,625					; 0,75								; 0,875
К3		3 max	0,625			3		; 0,75					3			; 0,875				3
						3							3							3

3 max 0,244; 0,089; 0,003 3 0,244 0,423.

P-value K3 0,64 .

3.9. Проверка конфликтов

Данный тест и тест парковок системы «DIEHARD» похожи, оба используют в своей основе задачи размещения.

Предположим, имеется a урн, в которые наудачу размещают b шаров, причем a b . Возможна ситуация, когда очередной шар будет размещен в урну, в которой уже есть шар. Данная ситуация называется «конфликтом». Существуют приближенная формула для оценки среднего числа конфликтов С в урне [11]

101

Сb2 . 2a

Также существует точная формула для расчета вероятности того, что произойдет ровно с конфликтов [11]:

pc a a 1 ... a b c 1	b
pc a a 1 ... a b c 1		.
an	b c

Сам тест заключается в сравнении числа конфликтов, производимых генератором, с ожидаемыми значениями. К сожалению, полученные значения очень сложно аппроксимировать с какимнибудь законом распределения, в связи с этим невозможно дать точную оценку результатам прохождения теста. В связи с этим для анализа конфликтов лучше использовать тест парковок из системы

«DIEHARD».

3.10. Проверка дней рождений

Данный тест полностью идентичен тесту «Проверка дней рождений» системы «DIEHARD».

3.11. Проверка корреляции

Данный тест проверяет взаимонезависимость элементов последовательности.

Пусть = 0, 1,…, n-1 – последовательность m-разрядных чисел

длины n. Вычисляется статистика

Сj

n 0 j 1 (1 j) mod n ... n 1

(n 1 j) mod n 0 1 ... n 1 2

n 02

12 ... n2

0 1 ... n 1 2

Для любого j значение Cj должно лежать в интервале

где

[ n 2 n ; n 2 n ] ,

n 1

n 1 2 n 2

Значение 2σ объясняется тем, что Д. Кнут считает, что если вероятность появления результата превышает 99 % (что имеет место в случае 3σ), то последовательность не является случайной. При 2σ вероятность появления результата равна 2Ф(2) = 2 · 0,4772 ≈ 95 %, что, по мнению Кнута, является приемлемым результатом.

102

Все вышеперечисленные тесты Д. Кнут отнес к эмпирическим критериям, то есть к критериям, при использовании которых осуществляются обработка формируемых генератором последовательностей и вычисление определенных статистик. Их анализ позволяет сделать определенные выводы о свойствах исследуемой последовательности и, как следствие, самого генератора. Кроме эмпирических, Д. Кнут рассматривает и теоретические критерии, для которых характеристики последовательности определяются при помощи теоретико-числовых методов, основанных на рекуррентных правилах, используемых при формировании последовательности. В отличие от эмпирических, теоретические критерии позволяют сделать заключение о свойствах последовательности еще до генерации, поскольку они анализируют не формируемую последовательность, а непосредственно структуру генератора. В этом и заключается их главный недостаток – теоретические критерии являются узкоспециализированными и не подходят для исследования генераторов со структурой, отличной от той, для которой был разработан критерий.

Теоретические критерии, предложенные Д. Кнутом в [11], ориентированы исключительно на тестирование простейших линейных конгруэнтных генераторов (LCG – linear congruential generator) [10]

с уравнением работы

Xi 1 aXi c mod n

103

Пример 3.10

Вход:

= 1 3 2 3 2; j = 2.

Тест:

C2 5 1 2 3 3 2 2 3 1 3 3 1 3 2 3 2 2 2 1, 5 12 32 22 32 22 1 3 2 3 2

5				1		0,25 ,
			5	1

	2				52		0,52 .
	5	5 1 2 5 2

и могут применяться лишь для отсеивания заранее некачественных генераторов при подготовке выборки для проверки эмпирическими критериями.

При этом к результатам теоретических критериев следует относиться с изрядной долей осторожности. В главе 7 приведены примеры статистических слабостей конгруэнтных генераторов, успешно прошедших теоретические критерии.

Также заслуживает внимания методика оценки результатов испытаний, предложенная Д. Кнутом. Если традиционно для теста выбирается уровень значимости и последовательность считается прошедшей тест при условии превышения значением P-value этого уровня, то Д. Кнут разбил значения P-value по интервалам. Для уровня значимости 0.01 эти интервалы следующие.

[0; 0,01) и (0,99; 1] – последовательность трактуется как неслучайная. Если с первым интервалом данное утверждение согласуется с общепринятой методикой, то второй интервал требует пояснения. Д. Кнут считает, что ситуация, когда последовательность «слишком случайна», то есть наблюдения полностью совпадают с ожидаемыми значениями, делает последовательность предсказуемой.

[0,01; 0,05) и (0,95; 0,99] – последовательность трактуется как «подозрительная». Оправданное деление, так как в ряде случаев вычисление статистики связано с использованием приближенных значений, и разница между точным и приближенным значением может привести к погрешности в вычислении P-value, и, как следствие, принятию неслучайной последовательности за случайную и наоборот.

[0,05; 0.1) и (0,9; 0,95] – последовательность трактуется как «почти подозрительная».

[0,1; 0,9] – последовательность трактуется как «случайная».

Если при исследовании генератора более половины последовательностей оказываются подозрительными, то генератор рассматривается как недостаточно случайный.

Данный подход оправдан только для P-value, имеющих значение в окрестности , где – уровень значимости теста. Для каче-

104

ственных последовательностей с увеличением их длины локальные неслучайные поведения, как правило, сглаживаются, в результате чего P-value стремится к окрестности 1. В связи с этим градацию Д. Кнута предпочтительнее изменить следующим образом:

[0; 0,01) – последовательность неслучайна;

[0,01; 0,05) – последовательность «подозрительна»;

[0,05; 0,1) – последовательность «почти подозрительна»;

[0,1; 1] – последовательность случайна;

105

ГЛАВА 4. РУКОВОДСТВО НИСТ

Проблема оценки статистических свойств генераторов псевдослучайных последовательностей настолько обширна, что к ее изучению подключаются целые институты. В мае 2001 года Национальным институтом стандартов и технологий (НИСТ) США был опубликован набор тестов для тестирования криптографических генераторов псевдослучайных последовательностей – A statistical test suite for random and pseudorandom number generators for cryptographic applications [15], в дальнейшем – Руководство НИСТ. В апреле 2010 года вышла новая ревизия данного набора [16]. Область применения данного набора – криптографические генераторы, говорит о силе тестов [15, 16, 36, 37], входящих в его состав.

По отношению к тестируемым последовательностям авторы Руководства делают следующие предположения.

Равномерность. В любой точке при генерации последовательности случайных или псевдослучайных битов 0 и 1 равновероятны и вероятности их появления равны 1/2. Ожидаемое число нулей (или единиц) равно n/2, где n – длина последовательности.

Масшабируемость. Любой тест, применимый к последовательности, может также применяться к произвольной подпоследовательности. Если последовательность случайна, то любая ее подпоследовательность должна также быть случайна. Следовательно, любая подпоследовательность должна пройти все тесты на случайность.

Полнота. Поведение генератора ПСП связано с начальным заполнением, поэтому неверно делать заключение о качестве генератора, основываясь на результатах анализа последовательности при каком-то одном начальном заполнении. Аналогично неверно делать заключение о генераторе случайных чисел, основываясь только на результатах анализа одного произведенного

им фрагмента последовательности.

Оценка статистических испытаний основана на проверке гипотезы о случайности исследуемой последовательности нулей и единиц. Табл. 4.1 показывает пошаговый процесс, позволяющий оценить конкретную двоичную последовательность.

106

Таблица 4.1. Процедура оценки

№		Пошаговый	Комментарии
шага		процесс	Комментарии
шага		процесс
1		Постановка	Предполагаем, что последовательность
1		гипотезы	является случайной
		гипотезы	является случайной
		Вычисление
2		тестовой статистики	Проводим тестирование на битовом уровне
		последовательности
3		Вычисление P-value	P-value [0; 1]

4		Сравнение	Задаем , где 0,001; 0,01 .
4		P-value с	Если P-value – тесты пройдены
		P-value с	Если P-value – тесты пройдены

В	состав Руководства		НИСТ входят следующие тесты

(табл. 4.2):

частотный (монобитный) тест (The Frequency (Monobit) Test);

частотный тест в подпоследовательностях (The Frequency Test within a Block);

проверка на равномерность (The Runs Test);

проверка на равномерность в подпоследовательностях (Test for the Longest-Run-of-Ones in a Block);

проверка рангов матриц (The Binary Matrix Rank Test);

спектральный тест (The Discrete Fourier Transform (Spectral) Test);

проверка непересекающихся шаблонов (The Non-overlapping Template Matching Test);

проверка пересекающихся шаблонов (The Overlapping Template Matching Test);

универсальный статистический тест Маурера (Maurer’s «Universal Statistical» Test);

Сжатие при помощи алгоритма Лемпела–Зива (The Lempel– Ziv Compression Test);

проверка линейной сложности (The Linear Complexity Test);

проверка серий (The Serial Test);

проверка аппроксимированной энтропии (The Approximate Entropy Test);

107

проверка кумулятивных сумм (The Cumulative Sums Test);

проверка случайных отклонений (The Random Excursions Test);

разновидность проверки случайных отклонений (The Random Excursions Variant Test).

Таблица 4.2. Статистические тесты Руководства НИСТ

№	Статистический тест	Определяемый дефект
1	Частотный тест	Слишком много нулей или единиц
2	Частотный тест	Слишком много нулей или единиц в подспосле-
	в подпоследовательностях	довательностях
	Проверка	Большое (малое) число подпоследовательностей
3	Проверка	нулей и единиц свидетельствует, что колебание
3	на равномерность	нулей и единиц свидетельствует, что колебание
		потока бит слишком быстрое (медленное)
	Проверка на равномер-	Отклонения в равномерности распределения ну-
4	ность в	Отклонения в равномерности распределения ну-
4	ность в	лей и единиц в подпоследовательностях
	подпоследовательностях	лей и единиц в подпоследовательностях
		Отклонение распределения рангов матриц от
5	Проверка рангов матриц	соответствующего распределения для истинно
		случайной последовательности, связанное с пе-
		риодичностью подпоследовательностей
6	Спектральный тест	Периодические свойства последовательности
	Проверка	Непериодические шаблоны встречаются слиш-
7	непересекающихся шабло-	Непериодические шаблоны встречаются слиш-
7	непересекающихся шабло-	ком часто
	нов
8	Проверка пересекающихся	Слишком часто встречаются m-битные последо-
	шаблонов	вательности единиц
9	Универсальный статисти-	Сжимаемость (регулярность) последовательности
	ческий тест Маурера
10	Сжатие при помощи	Большая сжимаемость, чем истинно случайная
10	алгоритма Лемпела–Зива	последовательность
11	Проверка	Отклонение от распределения линейной сложно-
	линейной сложности	сти для конечной длины (под)строки
12	Проверка серий	Неравномерность распределения m-битных слов.
	Проверка аппроксимиро-	Неравномерность распределения m-битных слов.
13	ванной энтропии	Малые значения означают высокую повторяе-
		мость
14	Проверка кумулятивных	Слишком много нулей или единиц в начале по-
	сумм	следовательности
15	Проверка случайных от-	Отклонение от распределения числа появлений
	клонений	подпоследовательностей определенного вида
16	Разновидность проверки	Отклонение от распределения числа появлений
16	случайных отклонений	подпоследовательностей определенного вида
		108

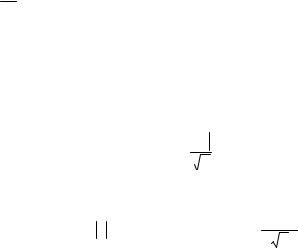
4.1. Частотный тест

Цель теста – проверить равномерность появления 0 и 1 в исследуемой последовательности.

Пусть = 1, 2,…, n – двоичная последовательность длины n. Представим ее в виде последовательности X = X1,X2,…,Xn, Xi = 2εi –

1, i 1,n . Вычислим сумму элементов последовательности X:

Sn Xi .

i 1

Примечание. При реализации теста значение Sn можно вычислять как разницу между числом появлений единиц n1 и нулей n0:

Sn = n1 – n0.

Вычислим статистику

s obs Snn ,

значение которой нормировано нормально распределено, поэтому соответствующее значение P-value есть

P-value z P-value s obs erfс s obs2 .

Значение P-value должно быть больше 0,01.

Рекомендуемая длина последовательности – не менее 100 бит.

Пример 4.1

Вход:

= 11001001000011111101101010100010001000010110100011 00001000110100110001001100011001100010100010111000;

n = 100.

Тест:

X = 1 1 –1 –1 1 –1 –1 1 –1 –1 –1 –1 1 1 1 1 1 1 –1 1 1 –1 1 –1 1 –1 1 –1 –1 –1 1 –1 –1 –1 1 –1 –1 –1 –1 1 –1 1 1 –1 1 –1 –1 –1 1 1 –1 –1 –1 –1 1 –1 –1 –1 1 1 –1 1 –1 –1 1 1 –1 –1 –1 1 –1 –1 1 1 –1 –1 –1 1 1 –1 –1 1 1 –1 –1 –1 1 –1 1 –1 –1 –1 1 –1 1 1 1 –1 –1 –1.

100

S100 Xi 16 . i 1

Альтернативный вариант вычисления S100 :

109

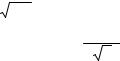
= 11001001000011111101101010100010001000010110100011 00001000110100110001001100011001100010100010111000.

Число единиц: n1 42 ; Число нулей: n0 58 .

S100 = n1 – n0 = 42 – 58 = – 16,

s obs		s100	1,6 ,


	100

P-value s obs erfс s obs2 0,109598 > 0,01 – тест пройден.

4.2. Частотный тест в подпоследовательностях

Цель теста – проверить равномерность появления 0 и 1 в подпоследовательностях.

Пусть = 1, 2,…, n – двоичная последовательность длины n.

Разобьем ее на N	n	непересекающихся М-битных подпосле-

M

довательностей. Лишние биты отбрасываем. Определим долю единиц в каждой подпоследовательности

	M
	ε i 1 M j
πi	j 1	, i		.
	j 1		1, N
	M		1, N
	M

Если последовательность случайна, то в каждой подпоследовательности доля единиц должна быть равна 0,5. Применим критерий

2 . Пусть Хi – число единиц в каждой подпоследовательности. Тогда

	N	Xi M 0,5 2		N	i	0,5 2
χ2 obs		Xi M 0,5 2	M 2		i	0,5 2	N	πi 0,5 2 .
	i 1			i 1			2M
		M 0,5		M 0,5			2M
		M 0,5		M 0,5			i 1

Данная статистика оценивается при помощи критерия 2 с N

степенями свободы (так как предполагается, что все подпоследовательности независимы).

Важное замечание. В Руководстве НИСТ в описании данного теста вычисляется статистика

110

χ2НИСТ obs 4M πi 0,5 2 .

i 1

Причины удвоения статистики не объясняются, при этом данное удвоение увеличивает силу теста.

Вычисляется статистика

P-value , 2 obs P-value N, 2 obs igamc	N	,	2 obs	.
P-value , 2 obs P-value N, 2 obs igamc		,		.
	2		2

Значение P-value должно быть больше 0,01.

Рекомендуемые параметры тестирования: длина последователь-

ности – не менее 100 бит. n > MN, M 20, M > 0,01n, N < 100.

Пример 4.2

Вход:

= 11001001000011111101101010100010001000010110100011

00001000110100110001001100011001100010100010111000; n = 100;

M = 10.

Тест:

N100 10 ,

1 = 1100100100, 1 104 ,

2 = 0011111101, 2 107 ,

3 = 1010101000, 3 104 ,

4 = 1000100001, 4 103 ,5 = 0110100011, 5 105 ,

6 = 0000100011, 6 103 ,

7 = 0100110001, 7 104 ,

111

8 = 0011000110, 8 104 ,9 = 0110001010, 9 104 ,

10 = 0010111000, 10 104 ,

2 obs 2 10 0,4 0,5 2 0,7 0,5 2 0,4 0,5 2 0,3 0,5 2

0,5 0,5 2 0,3 0,5 2 0,4 0,5 2 0,4 0,5 2 0,4 0,5 2

0,4 0,5 2 3,6,

P-value ,	2	obs P-value 10; 3,6		10	,	3,6
P-value ,		obs P-value 10; 3,6	igamс	2	,	2
				2		2

0,963593 > 0,01 – тест пройден.

2НИСТ obs 2 2 obs 2 3,6 7,2 .

P-value ,	2		10	,	7,2
P-value ,		obs P-value 10; 7,2 igamс	2	,	2
			2		2

0,706438 > 0,01 – тест пройден.

4.3. Проверка на равномерность

Цель теста – проверить равномерность распределения 0 и 1 в исследуемой последовательности на основе анализа количества появлений «блоков» – подпоследовательностей, состоящих из одних единиц, и «дырок» – подпоследовательностей, состоящих их одних нулей.

Пусть = 1, 2,…, n – двоичная последовательность длины n. Сначала определим предтестовую статистику * – долю единиц в рассматриваемой последовательности

* j 1n .

Если * 0.5 2n , то тест считается не пройденным (свя-

зано это с тем, что существенное превышение числа единиц, во-

112

первых, уже само по себе говорит о неслучайности последовательности, а во-вторых, не позволит оценить математическое ожидание и отклонение теоретических значений). В противном случае вычислим статистику (количество блоков и дырок)

n 1

n obs r k 1 ,

k 1

где r(k) = 0, если k = k+1 и r(k) = 1, если k k – 1.

Значение n obs аппроксимируется с нормальным законом распределения со средним

2n * 1 *

и отклонением

2 n * 1 * .

Вычисляем значение P-value нормированной нормальной вели-

чины

n obs 2n * 1 *

2 n * 1 *

n obs

P-value

n (obs) 2n

erfс

2n * 1 *

Значение P-value должно быть больше 0,01.

Рекомендуемая длина последовательности – не менее 100 бит.

Пример 4.3

Вход:

= 11001001000011111101101010100010001000010110100011 00001000110100110001001100011001100010100010111000;

n = 100.

Тест:

		2	0,2 ,
		100

* 10042 0,42 0,2 ,

113

100(obs) = 52,			52 2 100 0,42 1 0,42


P value erfс

			2 2 100 0,42 1 0,42

0,50079 > 0,01 – тест пройден.

4.4. Проверка на равномерность в подпоследовательностях

Цель теста – проверить равномерность распределения 0 и 1 в исследуемой последовательности на основе анализа количества появлений «блоков» в подпоследовательностях.

Пусть = 1, 2,…, n – двоичная последовательность длины n.

		n	непересекающихся М-битных подпосле-
Разделим ее на	N

	M

довательностей. Лишние биты отбрасываем. В Руководстве НИСТ предопределены три значения M (табл. 4.3), зависящие от длины исходной последовательности n.

Распределим число появлений подпоследовательностей с максимальной длиной «блока» (числом подряд идущих единиц), равной l, по категориям в соответствии с табл. 4.4.

Вычислим статистику

	2	,
2 obs i N i		,
K
i 0	N i

где i ( i 0, K ) – вероятность появления подпоследовательности с максимальной длиной блока, равной i. Значения i [34] приведены в табл. 4.5. Значения К выбираются в соответствии с табл. 4.6.

Полученная статистика оценивается при помощи критерия 2 с числом степеней свободы, равным N.

Таблица 4.3. Соотношение между M и минимальной длиной последовательности

min n		M

128		8

6272		128

750000		104
	114

Таблица 4.4. Распределение по категориям в зависимости от длины «блока»

		i				М = 8				М = 128					М = 104
		0				l 1				l 4					l 10
		1				l = 2				l = 5					l = 11
		2				l = 3				l = 6					l = 12
		3				l 4				l = 7					l = 13
		4								l = 8					l = 14
		5								l 9					l = 15
		6													l 16
	Таблица 4.5. Значения i для различных М и i
								M = 8
	0					1				2								3
0,2148					0,3672					0,2305				0,1875
							M =		128
	0			1		2				3			4					5
0,1174			0,2430			0,2493			0,1752		0,1027						0,1124
							M =		104
	0			1		2		3		4				5				6
0,0882		0,2092			0,2483		0,1933			0,1208		0,0675						0,0727

			Таблица 4.6. Соотношение между M и K
						M				K

					8					3

					128					5

					104					6
Вычислим значение P-value:																	2 obs
P-value , 2 obs P-value K, 2 obs igamc															K	,	2 obs		.
P-value , 2 obs P-value K, 2 obs igamc																,			.
														2			2

Значение P-value должно быть больше 0,01.

Рекомендуемая длина последовательности – не менее 100 бит. Значение M выбирается в соответствии с табл. 4.6.

115

Пример 4.4

Исходные данные:

= 11001100000101010110110001001100111000000000001001 00110101010001000100111101011010000000110101111100

1100111001101101100010110010; n = 128.

Тест:

По табл. 4.3 значению n = 128 соответствует M = 8. Значению M = 8 по таблице 4.6 соответствует K = 3.

	n	128
N			8	16.

M

Анализируем подпоследовательности:

1 = 11001100, максимальная длина «блока» = 2;2 = 00010101, максимальная длина «блока» = 1;3 = 01101100, максимальная длина «блока» = 2;4 = 01001100, максимальная длина «блока» = 2;5 = 11100000, максимальная длина «блока» = 3;6 = 00000010, максимальная длина «блока» = 1;7 = 01001101, максимальная длина «блока» = 2;8 = 01010001, максимальная длина «блока» = 1;9 = 00010011, максимальная длина «блока» = 2;10 = 11010110, максимальная длина «блока» = 2;11 = 10000000, максимальная длина «блока» = 1;12 = 11010111, максимальная длина «блока» = 3;13 = 11001100, максимальная длина «блока» = 2;14 = 11100110, максимальная длина «блока» = 3;15 = 11011000, максимальная длина «блока» = 2;

16 = 10110010, максимальная длина «блока» = 2.

Распределяем значения максимальных длин «блоков» по категориям:

0 = 4;1 = 9;2 = 3;

3 = 0.

Вычисляем статистику теста:

116

2 obs		4 16 0,2148 2				9 16 0,3672 2		4 16 0,2305 2
2 obs						16 0,3672
				16 0,2148		16 0,3672			16 0,2305
	0 16 0,1875 2				4,8826.
					4,8826.
	16 0,1875
Вычисляем значение P-value:
			2				3			4,8826
P-value ,				obs P-value 3, 4,8826 igamc					,
P-value ,				obs P-value 3, 4,8826 igamc					,	2
							2			2

0,18059 > 0.01 – тест пройден.

4.5. Проверка рангов матриц

Цель теста – проверить равномерность распределения 0 и 1 в исследуемой последовательности на основе анализа количества появлений матриц различных рангов.

Пусть = 1, 2,…, n – двоичная последовательность длины n.

		n
Разделим ее на	N		непересекающихся подпоследователь-

	M Q

ностей. Лишние биты отбрасываем. Теперь представим каждую такую подпоследовательность как бинарную матрицу размером

M Q.

Определим ранг каждой матрицы. Пусть FM – число матриц с рангом М,

FM–1 – число матриц с рангом М – 1,

N FM FM 1 – число оставшихся матриц. Вычислим статистику

2 obs		FM pM N 2			FM 1 pM 1N 2

		pM N				pM 1N
	N FM FM 1 pN FM				FM 1	N 2
							.
		pN F	F	N

		M	M 1

Значения соответствующих вероятностей можно определить по формуле, уже упоминавшейся в п. 1.3 при рассмотрении одноименного теста:

117

	i Q R i QR	i 1	1	2 j Q 1	2 j R
2						, i M 1 , M ;
2				1 2 j i		, i M 1 , M ;
pi		j 0		1 2 j i
	pM pM 1,					i N FM FM 1.
1	pM pM 1,					i N FM FM 1.

Полученный результат анализируется при помощи критерия 2 с числом степеней свободы, равным 2.

ВРуководстве НИСТ используются следующие значения для М

иQ:

M Q 32 .

Для данных значений получаем следующие вероятности:

p32	232 32	32	32	32 32		1 2	j 32	1 2	j 32	0,2888 ;
				32 1			j 32		j 32
p31	231 32	32		j 0	1 2		1 2 j 32			0,5776 ;
p31	231 32	32	31 32 32		1 2		j 32	1 2	j 32	0,5776 ;
				31 1			j 32		j 32
				j 0			1 2 j 31

p30 1 p32 p31 0,1336 .

Таким образом, формула для расчета статистики теста становится равной

2 obs		FM 0,2888N 2		FM 1 0,5776N 2
2 obs		0,2888N
		0,2888N			0,5776N
	N FM FM 1 0,1336N 2
					.
		0,1336N			.
		0,1336N
Вычисляем значение P-value:								2 obs
	2		2			2		2 obs
							,
P-value , obs P-value 2, obs igamс						2	,		2	.
						2			2

Значение P-value должно быть больше 0,01.

Рекомендуемая длина последовательности – не менее 38 M Q бит (для значений, рекомендуемых Руководством НИСТ не менее

38 32 32 = 38 912 бит).

4.6. Спектральный тест

Цель теста – проверить равномерность распределения 0 и 1 в исследуемой последовательности на основе анализа высоты выбросов преобразования Фурье.

118

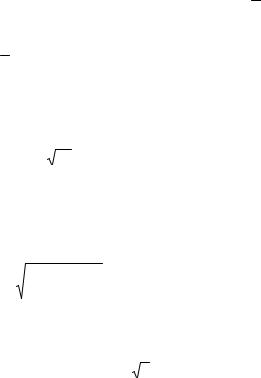
Пусть = 1, 2,…, n – двоичная последовательность длины n. Преобразуем ее в последовательность x = x1,x2,…,xn, где xi = 2 i – 1

(т.е. 1 1, 0 –1). Теперь применим к x дискретное преобразование Фурье и получим последовательность гармоник

S = DFT(x).

Пусть S – подпоследовательность S, содержащая первые n2 элементов S (гармоники симметричны, поэтому достаточно рассмотреть только первые n2 элементов). Для каждого элемента Si

найдем модуль Mi modulus(Si ) ( Si является комплексным чис-

лом). Последовательность M даст нам последовательность высот выбросов преобразования Фурье.

Найдем

	T		3n ,
	N0	0,95n			.

			2
Вычислим N1 – число элементов M, меньших, чем T.
Вычислим статистику	N1		N0
d							.
				0,05
	0.95					n

			2

Значение d нормировано нормально распределено, поэтому соответствующее значение P-value есть

P-value

erfс

Пример 4.5

Вход:

= 1001010011; n = 10.

Тест:

x = 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,

S = DFT(x),

119

	10							2									2
S1 xk				cos							k		1 i			sin					k 1				1,618 1,175i ,
S1 xk				cos				10			k		1 i			sin		10			k 1				1,618 1,175i ,
		k 1						10										10
	10						2 2												2 2
S2 xk				cos										k 1		i sin								k 1			1,381 4,253i ,
S2 xk				cos				10						k 1		i sin				10				k 1			1,381 4,253i ,
		k 1						10												10
	10						2 3												2 3
S3 xk				cos										k 1 i sin									k			1	0,618 1,902i ,
S3 xk				cos				10						k 1 i sin						10			k			1	0,618 1,902i ,
		k 1						10												10
	10						2 4													2 4
S4 xk cos														k 1		i sin								k	1		3,618 2,628i ,
S4 xk cos								10						k 1		i sin				10				k	1		3,618 2,628i ,
		k 1						10												10
	10								2								2											19
S5 xk				cos							k			1 i		sin					k 1					2 7,04 10			i ,
S5 xk				cos				10			k			1 i		sin		10			k 1					2 7,04 10			i ,
		k 1						10										10
M1 = modulus (1,618 – 1,175i) = 2,
M2 = modulus (1,381 – 4,253i) = 4,472,
M3 = modulus (–0,618 – 1,902i) = 2,
M4 = modulus (3,618 + 2,628i) = 4,472,
M5 = modulus (–2 – 7,04 10–19i ) = 2,
T		3 10				5,47 ,
N0	0,95 10 4,75 ,
	2
N1 = 5,
d		5 4,75										0,51,
d		0,95					0,05			10		0,51,
							0,05

						2
												d					0.51
												d					0.51
P-value			d		erfс										erfс							0,61				> 0,01 – тест пройден.


													2					2
													2					2

4.7. Проверка непересекающихся шаблонов

Цель теста – проверить равномерность распределения 0 и 1 в исследуемой последовательности на основе анализа частоты встречаемости заранее определенных шаблонов.

Пусть = 1, 2,…, n – двоичная последовательность длины n.

120

		n	непересекающихся М-битных подпосле-
Разобьем ее на	N

	M

довательностей. Лишние биты отбрасываются.

Пусть j – количество появлений шаблона (подпоследовательности определенного типа) в j-й подпоследовательности ( j 1, N ).

Поиск осуществляется следующим образом. Пусть m – размер шаблона в битах. Начинаем сканировать j-ю подпоследовательность. Если рассматриваемый набор

N(j – 1) + k, …, N(j – 1) + k + m – 1, k 1, M m 1,

совпадает с шаблоном, то значение j увеличиваем на 1 и рассматриваем набор

N(j – 1) + k + m, …, N(j – 1) + k + 2m – 1,

в противном случае значение j не изменяем и рассматриваем набор

N(j – 1) + k + 1, …, N(j – 1) + k + m.

Сканирование прекращаем, когда часть элементов набора выходит за пределы рассматриваемой подпоследовательности.

Значения j аппроксимируются с нормальным распределением со следующими параметрами:

	M m 1 ,
		2m	2m 1
2		1	2m 1
	M			.
	M	2m	22m	.
		2m	22m

Вычислим статистику

2 obs N j 2 2

j 1

и значение P-value

P-value , 2 obs P-value N, 2 obs igamc N ,

Значение P-value должно быть больше 0,01.

2 obs .

Рекомендуемые параметры тестирования: N 100, M > 0,01n. Значения шаблонов, используемые в программной реализации

данного теста, приведены в табл. 4.7.

121

Таблица 4.7. Значения шаблонов для теста непересекающихся шаблонов


		4		m
2	3	4	5	6	7		8
01	001	0001	00001	000001	0000001	00000001		11010010
10	011	0011	00011	000011	0000011	00000011		11010100
	100	0111	00101	000101	0000101	00000101		11011000
	110	1000	01011	000111	0000111	00000111		11011010
		1100	00111	001011	0001001	00001001		11011100
		1110	01111	001101	0001011	00001011		11100000
			11100	001111	0001101	00001101		11100010
			11010	010011	0001111	00001111		11100100
			10100	010111	0010011	00010011		11100110
			11000	011111	0010101	00010101		11101000
			10000	100000	0010111	00010111		11101010
			11110	101000	0011011	00011001		11101100
				101100	0011101	00011011		11110000
				110000	0011111	00011101		11110010
				110010	0100011	00011111		11110100
				110100	0100111	00100011		11110110
				111000	0101011	00100101		11111000
				111010	0101111	00100111		11111010
				111100	0110111	00101011		11111100
				111110	0111111	00101101		11111110
					1000000	00101111
					1001000	00110101
					1010000	00110111
					1010100	00111011
					1011000	00111101
					1011100	00111111
					1100000	01000011
					1100010	01000111
					1100100	01001011
					1101000	01001111
					1101010	01010011
					1101100	01010111
					1110000	01011011
					1110010	01011111
					1110100	01100111
					1110110	01101111
					1111000	01111111
					1111010	10000000
					1111100	10010000
					1111110	10011000
						10110100
						10111000
						10111100
						11000000
						11000010
						11000100
						11001000
						11001010
						11010000
				122

Примечание. Данный тест можно существенно усилить, если вычислить значения P-valuej для каждой подпоследовательности

, ,

M m 1

2m 1

P-value

22m

m 1

erfс

2m 1

а затем применить к полученным значениям критерий Колмогоро- ва–Смирнова или Андерсона–Дарлинга.

Пример 4.6

Вход:

= 1010010010111001011010; n = 22;

M = 10;

m = 3, шаблон равен «001».

Тест:

N22 2 .

Последние два бита (10) отбрасываем, как не принадлежащие ни к одной подпоследоательности.

1 = 1010010010,2 = 1110010110.

Определим число появлений шаблона «001»

Позиции	1 = 1010010010		2 = 1110010110
битов	биты	1	биты	2
1–3	101	0	111	0
2–4	010	0	110	0
3–5	100	0	100	0
4–6	001	1 (+1)	001	1 (+1)
5–7	Пропуск	1	Пропуск	1
6–8	Пропуск	1	Пропуск	1
7–9	001	2 (+1)	011	1
8–10	010	2	110	1
		123

10 3 1						1,
		23					2 3 1
	2		1				2 3 1		0,46875 ,
		10
		10	23				22 3
			23				22 3		1 1 2
2 obs				2 1 2					1 1 2	2,1 3 ,
2 obs								0,46875		2,1 3 ,
			0,46875					0,46875						2,1 3
P-value ,					2	obs						2		2,1 3
								P-value 2; 2,1(3)			igamc		,
								P-value 2; 2,1(3)			igamc	2	,	2
												2		2

0,3441> 0,01 – тест пройден.

4.8. Проверка пересекающихся шаблонов


Пусть	= 1, 2,…, n	– двоичная последовательность длины n.
	n	непересекающихся М-битных подпосле-
Разобьем ее на N

	M
довательностей. Лишние биты отбрасываем.
Пусть i	– число подпоследовательностей, в которых шаблон

появляется i раз ( i 0, K , K – число степеней свободы, в K запи-

сывается число подпоследовательностей, в которых шаблон встречается К и более раз). Поиск осуществляется следующим образом. Пусть m – размер шаблона в битах. Начинаем сканировать j-ю под-

последовательность, j 1, N . Рассматриваем пересекающиеся на-

боры по m бит. Находим

M m 1 , . 2m 2

Вычисляем статистику

	2	,
2 obs i N i		,
K
i 0	N i
124

		e		i i 1	l
где i						, которую анализируем при помощи крите-
			i
			i
		2		l 1 l 1	l!
рия 2	с числом степеней свободы, равным K.
Вычислим значение P-value									2 obs
P-value , 2 obs P-value K, 2 obs igamc							K	,	2 obs	.
P-value , 2 obs P-value K, 2 obs igamc								,		.
						2			2

Значение P-value должно быть больше 0,01.

Рекомендуемые параметры тестирования: n MN, N min( i) > 5,

2, m log2M, K 2 .

Пример 4.7

Вход:

= 10111011110010110100011100101110111110000101101001101; n = 53;

M = 10;

m = 2, шаблон равен «11»;

K = 5.

Тест:

N53 5 .10

Последние три бита (101) отбрасываем как не принадлежащие ни к одной подпоследовательности.

0 = 0, 1 = 0, 2 = 0, 3 = 0, 4 = 0, 5 = 0;

Найдем число появлений шаблонов в 1-й подпоследовательности

1 = 1011101111.

Позиции битов	Биты		Число появлений шаблона
1–2	10		0
2–3	01		0
3–4	11		1 (+1)
4–5	11		2 (+1)
5–6	10		2
6–7	01		2
7–8	11		3 (+1)
8–9	11		4 (+1)
9–10	11		5 (+1)
		125

0 = 0, 1 = 0, 2 = 0, 3 = 0, 4 = 0, 5 = 1.

Найдем число появлений шаблонов во 2-й подпоследовательности

2 = 0010110100.

Позиции битов	Биты	Число появлений шаблона
1–2	00	0
2–3	01	0
3–4	10	0
4–5	01	0
5–6	11	1 (+1)
6–7	10	1
7–8	01	1
8–9	10	1
9–10	00	1

0 = 0, 1 = 1, 2 = 0, 3 = 0, 4 = 0, 5 = 1.

Найдем число появлений шаблонов в 3-й подпоследовательности

3 = 0111001011.

Позиции битов	Биты	Число появлений шаблона
1–2	01	0
2–3	11	1 (+1)
3–4	11	2 (+1)
4–5	10	2
5–6	00	2
6–7	01	2
7–8	10	2
8–9	01	2
9–10	11	3 (+1)

0 = 0, 1 = 1, 2 = 0, 3 = 1, 4 = 0, 5 = 1.

Найдем число появлений шаблонов в 4-й подпоследовательности

4 = 1011111000.

Позиции битов	Биты		Число появлений шаблона
1–2	10		0
2–3	01		0
3–4	11		1 (+1)
4–5	11		2 (+1)
5–6	11		3 (+1)
6–7	11		4 (+1)
7–8	10		4
8–9	00		4
9–10	00		4
		126

0 = 0, 1 = 1, 2 = 0, 3 = 1, 4 = 1, 5 = 1.

Найдем число появлений шаблонов в 5-й подпоследовательности

5 = 0101101001.

			Позиции битов														Биты									Число появлений шаблона
						1–2												01											0
						2–3												10											0
						3–4												01											0
						4–5												11										1 (+1)
						5–6												10											1
						6–7												01											1
						7–8												10											1
						8–9												00											1
						9–10												01											1
	0 = 0, 1 = 2, 2 = 0, 3 = 1, 4 = 1, 5 = 1.
10 2 1							2,25 ,
					22
		2,25				1,125 ,
						1,125 ,
			2				1		l
			e			0	1		l									1,125
0											e					e						0,324652 ,
					0
			2		0				l!
			2			l 1 l	1		l!
			e			1	0		l					e						e 1.125
1				1																			0,182617 ,
1				1					l!						2							2	0,182617 ,
			2			l 1 l	1		l!						2							2
			e 2				1		l			e							2					e
2																										( 2)
					2
			2		2				l!				4							2					8
			2			l 1 l 1			l!				4							2					8
1,125 e 1,125							1,125 2 0,142670,
						8
			e			3	2		l			e										2		3			e	2
3			e									e					2										e
					3
			2		3				l!				8								2		3!				8	6	1
			2			l 1 l		1	l!				8								2		3!				8	6
1,125 e						1,125				2
1,125 e							1,125				1,125 1									0,106645,
						8		6
						8		6
																						127

		e 4 3									l				e				2		3		4
4																	3			3
			4
		2	4								l!				16				2!		3!
		2			l 1		l 1				l!				16				2!		3!		4!
	e					3			2				3
	e												3
	16				24			2				2		1
	16				24			2				2
1,125 e				1,125								3				2		3
								1,125						1,125				3	1,125 1			0,077147,
														1,125					1,125 1			0,077147,
					16					24					2			2
					16					24					2			2

5 1 0 1 2					3 4 1 0,324652 0,182617 0,142670
0,106645 0,077147 0,166269,
2 obs		0 5 0,324652 2					2 5 0,182617 2				0 5 0,142670 2

				5 0,324652			5 0,182617						5 0,142670
	1 5 0,106645 2					1 5 0,077147 2			1 5 0,166269 2					5,6656,
	5 0,106645					5 0,077147			5 0,166269

P-value ,			2	obs	P-value 5; 5,6656					5		,	5,6656
								igamc		2			2

0,340129 > 0,01 – тест пройден.

4.9. Универсальный статистический тест Маурера

Цель теста [33] – проверить равномерность распределения 0 и 1 в исследуемой последовательности на основе анализа расстояний между шаблонами.

Пусть = 1, 2,…, n – двоичная последовательность длины n. Разобьем ее на два сегмента: инициализирующий и тестовый. Пер-

вый состоит из Q блоков по L бит, второй – из	n
	K	Q	блоков

	L

по L бит. Лишние биты отбрасываем.

Инициализирующий сегмент используется для создания таблицы Т. Для i 1, Q Tj = i, где j есть десятичное представление i-го L-

ричного блока.

После этого переходим к сканированию тестового блока. Проверяем каждый из К блоков и определяем расстояние в блоках от последнего появления данного i-го блока (т.е. i – Tj), одновременно обновляя таблицу: Tj = i.

128

Вычисляем статистику

fn 1 Q Klog2 i Tj , K i Q 1

Величина fn аппроксимируется с нормальным распределением, поэтому можно вычислить значение P-value со средним

expectedValue и ожиданием :

P-value

fn expectedValue

P-value

fn expectedValue

erfс

0.8

variance L

32 K L

где 0.7

L 15

Значения expectedValue и variance берутся из табл. 4.8. Значение P-value должно быть больше 0,01.

Рекомендуемые параметры тестирования следующие указаны в табл. 4.9.

Таблица 4.8. Значения expectedValue и variance

L	expectedValue	variance
1	0,7326495	0,690
2	1,5374383	1,338
3	2,4016068	1,901
4	3,3112247	2,358
5	4,2534266	2,705
6	5,2177052	2,954
7	6,1962507	3,125
8	7,1836656	3,238
9	8,1764248	3,311
10	9,1723243	3,356
11	10,170032	3,384
12	11,168765	3,401
13	12,168070	3,410
14	13,167693	3,416
15	14,167488	3,419
16	15,167379	3,421
	129

1 / 51 2 3 4 5 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
12.11.20221.43 Mб4Хотеева Научное познание в историко-философском контексте 2011.pdf
#
12.11.2022738.85 Кб2Цавелов Стсинтиллятсионные кристаллы для плазмофизического експеримента 2015.pdf
#
12.11.20221.65 Mб3Целисчев Лабораторный практикум Конструкционные материалы ядерных реакторов 2012.pdf
#
12.11.202212.4 Mб0Цолнцева Тхе Импортанце оф Беинг Еарнест бы Осцар Wилде 2013.pdf
#
12.11.20222.39 Mб2Цывкунова АРМС ЦОНТРОЛ АНД ДИСАРМАМЕНТ 2013.pdf
#
12.11.20224.26 Mб14Чугунков Методы и средства оценки качества генераторов 2012.pdf
#
12.11.20222 Mб1Чучкина Инноватион течнологиес 2011.pdf
#
12.11.2022497.8 Кб1Чучкина Хоw то маке а пресентатион 2011.pdf
#
12.11.20221.36 Mб12Шапкарин Лабораторный 2012.pdf
#
12.11.20225.86 Mб5Шведенко Начала математического анализа 2011.pdf
#
12.11.202210.65 Mб15Шелегов Насосное оборудование АЕС 2011.pdf

n						k
n	0	1	2	3	4		5	6	7	9	0
	0	1	2	3	4		5	6	7	9	0
0	1	0	0	0	0		0	0	0	0	0
1	1	1	0	0	0		0	0	0	0	0
2	1	2	1	0	0		0	0	0	0	0
3	1	3	3	1	0		0	0	0	0	0
4	1	4	6	4	1		0	0	0	0	0
5	1	5	10	10	5		1	0	0	0	0
6	1	6	15	20	15		6	1	0	0	0
7	1	7	21	35	35		21	7	1	0	0
8	1	8	28	56	70		56	28	8	1	0
9	1	9	36	84	126		126	84	36	9	1
					10

n						k
n	0	1	2	3	4		5	6	7	9	0
	0	1	2	3	4		5	6	7	9	0
0	1	0	0	0	0		0	0	0	0	0
1	1	1	0	0	0		0	0	0	0	0
2	1	2	1	0	0		0	0	0	0	0
3	1	3	3	1	0		0	0	0	0	0
4	1	4	6	4	1		0	0	0	0	0
5	1	5	10	10	5		1	0	0	0	0
6	1	6	15	20	15		6	1	0	0	0
7	1	7	21	35	35		21	7	1	0	0
8	1	8	28	56	70		56	28	8	1	0
9	1	9	36	84	126		126	84	36	9	1
					10

n						k
n	0	1	2	3	4		5	6	7	9	0
	0	1	2	3	4		5	6	7	9	0
0	1	0	0	0	0		0	0	0	0	0
1	1	1	0	0	0		0	0	0	0	0
2	1	2	1	0	0		0	0	0	0	0
3	1	3	3	1	0		0	0	0	0	0
4	1	4	6	4	1		0	0	0	0	0
5	1	5	10	10	5		1	0	0	0	0
6	1	6	15	20	15		6	1	0	0	0
7	1	7	21	35	35		21	7	1	0	0
8	1	8	28	56	70		56	28	8	1	0
9	1	9	36	84	126		126	84	36	9	1
					10