Ратушный Методы получения епитаксиалных гетерокомпозиций 2012

пературе газовую фазу называют пересыщенной, если ее давление превышает равновесное давление насыщенных паров жидкой или твердой фаз. При этом кристаллизация (например, при затвердевании расплава или конденсации пара) обычно не протекает однородно во всем объеме метастабильной фазы [2].

Как уже отмечалось, в начале процесса в разных местах исходной фазы образуются центры кристаллизации, которые затем разрастаются благодаря процессам тепло- и массопередачи. Создание пересыщения (переохлаждения) для кристаллизации исходной фазы необходимо для сообщения системе дополнительной энергии, требуемой для образования поверхности зародышей новой фазы.

Механизм образования зародышей новой фазы может быть гомогенным, когда в исходной фазе отсутствуют какие-либо твердые частицы или поверхности, стимулирующие образование на них центров, и гетерогенным, когда они присутствуют.

Рассмотрим основные параметры, определяющие условия фазового превращения при гомогенном образовании центров кристаллизации.

Вразличных точках газообразной, жидкой или твердой, молекулярной или атомной системы, находящейся в состоянии теплового равновесия, непрерывно возникают флуктуации, т.е. отклонения различных величин от их наиболее вероятных значений. Флуктуации плотности или концентрации в исходной фазе могут приводить

кизменению фазового состояния (например, образование зародышей новой фазы). В этом случае говорят о гетерофазных флуктуациях. Когда изменения фазового состояния в результате флуктуации не происходит, их называют гомофазными. Возникновение гетерофазных флуктуации сопровождается изменением свободной энергии системы не только вследствие различия энергии частиц в различных состояниях, но также и за счет образования поверхности раздела s [22].

Впроцессе образования зародышей новой фазы как энергетический критерий возможности протекания процессов используется свободная энергия Гиббса. Движущей силой любого фазового превращения является стремление системы к уменьшению свободной энергии G. Имеется её три составные части: объёмная, поверхностная и упругой деформации, обусловленная структурными изменениями твердого тела. Первые два фактора наиболее значимы. Для

31

протекания фазового превращения необходимо, чтобы свободная энергия единицы объема исходной фазы была больше свободной энергии такого же объема новой фазы. Кроме того, следует учитывать, что при образовании частиц новой фазы обязательно возникают поверхности раздела между новой и исходной фазами. Эти поверхности обладают поверхностной энергией, что затрудняет превращение. Поэтому в общем виде суммарное изменение свободной энергии системы при фазовом превращении

μконд, μпара – химические потенциалы соответственно конденсированного (твердого) вещества и пара.

где σ – поверхностное натяжение конденсируемой твердой фазы; Ω – площадь её поверхности.

Таким образом

новой фазы происходить не будет из-за G > 0.

Гомогенной конденсацией называется выделение вещества на собственных, возникающих на поверхности зародышах, в отличие от гетерогенного процесса, когда новая фаза конденсируется на уже имеющихся центрах, например, частицах пыли и пр.

При условии пересыщения (P > Pнас = P∞) будем иметь μконд < μпара и возникновение новой фазы зависит от поверхностной составляющей энергии, т.е. от размеров зародыша, определяющих поверхностную энергию.

Для сферического зародыша:

32

Для исследования зависимости энергии Гиббса от размера зародыша r с целью установления наличия её экстремумов приравняем производную к нулю:

где μ0i – стандартный химический потенциал при нормальном атмосферном давлении; рi – парциальное давление i-го компонента; R – молярная газовая постоянная; Т – температура.

С учетом (2.6), получим

Откуда критический радиус зародыша rкр. равен:

Давление Pкрпар должно быть равно давлению насыщенного пара

над поверхностью зародыша с размером rкр. Определим знак экстремума (max или min), найдя вторую производную функции:

Отрицательный знак второй производной свидетельствует о том, что G = ƒ(r) проходит через точку максимума (рис. 2.3), в которой наблюдается неустойчивое равновесие между двумя фазами: слева от максимума выгоднее испарение зародышей, а справа – их выделение.

33

Капельки радиусом меньше критического (или в общем случае участки новой фазы размером меньше критического) называют за-

родышами, а больше критического – центрами новой фазы (или в случае кристаллизации – центрами кристаллизации).

Если Р/Р∞<1, то G возрастает с увеличением r и капельки любых размеров, возникающие в результате гетерофазных флуктуации, будут проявлять тенденцию к испарению [2].

Таким образом, зародыш новой фазы может появиться и расти только в условиях, когда свободная энергия вещества в новой фазе меньше свободной энергии того же вещества в исходной фазе: паровой, растворе или расплаве.

Поскольку свободная энергия не может быть непосредственно измерена, для определения условий образования зародышей и их дальнейшего роста пользуются понятиями пересыщения и переохлаждения. Для зарождения и роста кристаллов необходимо, чтобы исходная фаза была пересыщена или переохлаждена по отношению к возникающей в ней твердой фазе. Напомним, что при данной температуре газовую фазу называют пересыщенной, если ее давление Р превышает давление Р0 насыщенных паров жидкой или твердой фазы [2]. Для начала гомогенного зарождения критический коэффициент пересыщения α = Р / Р0 составляет величину порядка

десяти. Однако в реальных условиях этот коэффициент намного ниже. Это обусловлено наличием в системе примесей, либо наличие готовых поверхностей раздела за счет присутствия инородных нерастворимых частиц.

Примеси, растворенные в зародыше новой фазы, влияют на объемную и поверхностную составляющие изменения свободной энергии при зародышеобразовании. Влияние примесей на процессы роста кристаллов проявляется весьма многообразно, что значительно затрудняет изучение механизма этого процесса. Значительную роль здесь играют природа примеси, ее концентрация, зарядовое состояние. В одних случаях примеси ускоряют рост кристаллов, в других – замедляют. Поверхностно-активные примеси, как правило, понижают свободную поверхностную энергию. Адсорбированная примесь может ослаблять связь конденсата с подложкой, а в других – увеличивать ее.

Рассмотрим теперь процесс гетерогенного образования зародышей при конденсации пересыщенного пара на гладкую плоскую

35

чистую подложку. В общем случае зародыш, образующийся на поверхности подложки, будет иметь либо форму шарового сегмента радиусом r, либо форму монослойного диска.

Изменение свободной энергии системы при гетерогенном образовании зародыша [16]:

где θ – равновесный угол смачивания.

Случай θ = 180° соответствует полной несмачиваемости подложки жидкостью. Это возможно, когда взаимодействие между атомами или молекулами этих материалов мало по сравнению с их взаимодействием в жидкости. В этом случае нет никакого энергетического выигрыша, и подложка не оказывает каталитическое действие на процесс зародышеобразования.

В случае θ = 0° новая фаза полностью смачивает подложку. При этом взаимодействие между атомами или молекулами зародыша и подложки превышает взаимодействие между атомами или молекулами в зародыше. При этом на подложке будут образовываться двумерные зародыши в виде монослойных дисков.

Энергия активации образования монослойного диска критического размера:

где γпт, γжт и γжп – удельные свободные поверхностные энергии границ раздела пар–твердое, жидкость–твердое и жидкость–пар соответственно; εпж – удельная свободная энергия моноатомной ступени; h – ее высота.

Случай 0 ≤ θ ≤180° всегда энергетически более выгоден, чем гомогенное зародышеобразование. Здесь критический радиус зародыша тем меньше, чем меньше угол θ. В данном случае подложка выступает в роли катализатора для процесса зародышеобразования.

Проведенный анализ гетерогенного зародышеобразования новой фазы при конденсации жидких капель применим и для анализа гетерогенного образования кристаллических зародышей из газовой

36

и жидкой фаз. Однако при этом равновесная форма зародышей бу-

Для описания достаточно медленных процессов конденсации тонких пленок совсем не обязательно использовать детальные микроскопические теории быстрых процессов – адсорбции, десорбции и диффузионных перескоков адатомов в соседние узлы. Вполне достаточно знать усредненное макроскопическое поведение адсорбированных частиц.

Обычно первым этапом конденсации пленок считают адсорбцию. При конденсации из однокомпонентного пара чаще всего различают мономолекулярную и диссоциативную адсорбции, которые при малых числах заполнения подложки приводят к равномерному возникновению адатомов по всей незанятой поверхности подложки с постоянной скоростью

где Р – давление пара; Тv – его температура; М – масса одной осаждаемой молекулы; kB – константа Больцмана; Cg – геометрический фактор.

Адсорбированные атомы могут либо десорбироваться обратно в пар, либо перескочить в один из соседних узлов (диффундировать). В случае однокомпонентных пленок различают мономолекулярную и ассоциативную десорбции, которые соответственно описываются следующими уравнениями:

где n1 – поверхностная концентрация адатомов; t – время (dn1/dt – скорость десорбции); τr – характерное время мономолекулярной десорбции (время реиспарения); Dd – коэффициент ассоциативной десорбции, имеющий размерность коэффициента диффузии; Еa – энергия активации десорбции; v и Dd0 – предэкспоненциальные факторы [23].

Среднее расстояние, на которое перемещается диффундирующий атом за время t, равно

37

где Da – коэффициент диффузии адатомов; Ed – энергия активации диффузии (как правило, она примерно равна Еa/3); Da0 – предэкспоненциальный фактор.

Значения энергий активации и предэкспоненциальных множителей для различных систем можно найти, например, в [23].

Рассмотрим кинетику заполнения поверхности подложки адатомами при отсутствии роста тонкой пленки, т.е. при n1<n1e, где n1e

– равновесная концентрация адатомов. При постоянной скорости J поступления адатомов на подложку и малых числах заполнения подложки для случаев мономолекулярной и ассоциативной десорбции соответственно имеем:

Для простоты, если не оговорено особо, обычно рассматривают только случай мономолекулярной десорбции, который чаще встречается на практике.

2.3. Основные режимы роста тонких эпитаксиальных пленок

Режимы роста тонких пленок обычно разделяются на послойный, островковый и промежуточный (рис. 2.4).

Послойный режим (layer-by-layer growth), или режим Франка– Ван дер Мерве (Frank–Van der Merve, FM) реализуется в том случае, если атомы осаждаемого вещества связаны с подложкой более сильно, чем друг с другом. В этом случае сумма поверхностной энергии осаждаемой плёнки и энергии гетерограницы меньше, чем

38

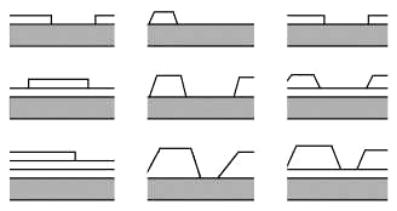
поверхностная энергия подложки. Моноатомные слои заполняются в этом режиме по очереди, т.е. двумерные зародыши (толщиной в один атом) следующего слоя образуются на верхней части зародышей предыдущего слоя после его заполнения (рис. 2.4 а). Послойный рост используется для выращивания большинства традиционных слоистых гетероструктур.

а б в

Рис. 2.4. Схемы трех важнейших механизмов роста [17]:

а – послойный режим; б – островковый режим; в – промежуточный режим

Островковый режим (рис. 2.4, б), или режим Фольмера–Вебера

(island growth, Vollmer–Weber, VW), реализуется в противополож-

ном случае, когда атомы осаждаемого вещества связаны между собой сильнее, чем с подложкой. В островковом режиме маленькие зародыши образуются прямо на поверхности подложки и затем растут, превращаясь в большие островки конденсированной фазы. После чего, сливаясь, эти островки образуют после заполнения каналов между ними сплошную пленку.

Согласно теории Фольмера, начальные стадии образования пленки твердого вещества посредством его конденсации из газовой фазы происходит по «островковому» механизму роста. При этом размер зародыша строго регламентируется термодинамическими условиями роста, в частности, условиями пересыщения осаждаемого вещества в газовой фазе. В свою очередь, размер зародыша и определяет возможности данного процесса по прецизионности рос-

39

та. Другими словами, процесс не может обеспечить точность осаждения сплошной пленки лучше, чем размер зародыша.

В промежуточном режиме (рис. 2.4, в), или режиме Странско-

го–Крастанова (Stransky–Krastanov, SK, layer-plus-islandgrows),

сначала реализуется послойный рост, затем после заполнения од- ного-двух слоев начинается рост трехмерных островков пленки. Причин смены механизмов роста может быть несколько. Однако основной из них считается достаточно большое несоответствие между параметрами кристаллических решеток пленки и подложки.

При данном механизме роста материал на поверхности слоя будет собираться в островки, которые будут выгибаться в вакуум. Если островки-пучности разного размера, содержат дефекты, то такая система неприменима для совершенных полупроводниковых структур. Однако, данный механизм роста с успехом применяется для получения лазеров на квантовых точках. Ключевым фактором в данном случае является не только снижение упругой энергии при формировании островков, но и изменение поверхностной энергии, связанное с их упругой релаксацией.

Зародыши на подложке могут иметь различную форму, однако чаще всего в теоретических расчетах полагают, что они имеют форму либо диска, либо полусферы, в зависимости от механизма роста пленки. Это связано с тем, что многие пленки растут по механизму пар → жидкость → кристалл.

Условие, разграничивающее реализацию того или иного механизма роста, можно получить из анализа соотношений между коэффициентами поверхностного натяжения между подложкой и вакуумом σS, между пленкой и вакуумом σF и между подложкой и пленкой σS/F (рис. 2.5). Коэффициент поверхностного натяжения поверхности равен свободной энергии единицы поверхности. Соответственно эти коэффициенты определяют силы поверхностного натяжения, действующие на единицу элемента длины границы раздела. Согласно этому определению сила dF, действующая на бесконечно малый элемент dl границы раздела двух сред, определяется как dF = σ dl.

Из условия равновесия для любого элемента длины линии соприкосновения подложки, трехмерного островка пленки и вакуума (см. рис. 2.5) получим:

40