Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный исследовательский ядерный университет (МИФИ)

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Михайлов ТФКП Практикум 2013

.pdf

Скачиваний:

Добавлен:

12.11.2022

Размер:

3.91 Mб

Скачать

☆

<<< < Предыдущая 1 2 34 / 254 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

		cos φ	1
∂φ	=	sin φ	0	= −	sin φ	.
∂x	=	ρ		= −		.
∂x		ρ			ρ

Таким образом,

∂u

= nρn−1 cos nφcos φ−nρn sin nφ −

sin φ

∂x

= nρn−1 (cos nφcos φ+sin nφsin φ) = nρn−1 cos(n −1)φ .

∂υ = nρn−1 ∂ρsin nφ+ nρn cos nφ

∂φ ;

∂y

∂ρ

cosφ−ρsin φ

∂φ

−ρsin φ

0 =

∂y

∂ρ

ρcos φ

= sin φ;

∂ρsin φ+ρcosφ∂φ

∂y

1 =

∂y

cos φ

∂φ

sin φ

cos φ

∂y

откуда

∂υ = nρn−1 sin nφsin φ

+nρn cos nφ

cos φ

= nρn−1 cos(n −1)φ.

∂y

Таким образом, ∂u

= ∂υ .

∂x

∂y

Аналогично проверяется условие

∂u

= −

∂υ .

∂y

∂x

Ввиду

непрерывности

частных

производных

производную

w'(z) можно вычислить, например, по формуле w'(z) = ∂u +i

∂υ .

∂x

Подсчитав, что ∂∂υx = nρn−1 sin (n −1)φ, получим:

(zn )' = nρn−1 cos(n −1)φ+inρn−1 sin(n −1)φ= nzn−1 ,

что и требовалось доказать.

Производную легко получить и непосредственно, пользуясь определением:

(zn ) ' = lim

= lim (z +

z)n − zn

→0

z→0

= lim

zn +nzn−1

z +

− zn

= nzn−1.

→0

Рассмотрим

функцию

w = ez

= ex+iy = exeiy = ex (cos y +i sin y) ;

u(x, y) = ex cos y ; υ(x, y) = ex sin y .

Условия Коши–Римана выполняются, так как

∂u = ex cos y =

∂υ

= ex cos y

∂u = −ex sin y = −

∂υ

= −ex sin y .

∂x

∂y

∂x

Следовательно,

)' =

∂u

∂υ

∂x

∂x = e

cos y +ie

sin y = e

Рассмотрим функцию w = Ln z = ln ρ+ iφ+ i2πk .

u ( x, y) = ln x2 + y2 ;

v ( x, y) = φ + 2πk ;

∂u =

= cos φ ;

∂υ

∂φ

= cos φ (см. выше).

x2 + y2

∂y

∂x

Аналогично:

∂u

= sin φ

;

∂υ = ∂φ

= −sin φ .

∂y

+ y2

∂x

Условия Коши–Римана выполнены:

(Lnz)' = ∂u

+i ∂υ = cos φ

−i sin φ =

ρcos φ −i

ρsin φ =

∂x

ρ2

−i

x −iy

= 1 .

x2 + y2

+ y2

x2 + y2

Эту производную можно было вычислить по правилу производной для обратной функции. Действительно, если w = w(z) , то об-

ратная функция z = z−1 (w) имеет производную:

w'( z) = lim	w = lim	1	=			1			;
		w		(		(		))
z→0
	z w→0	z			z−1		w	′

так как w = Ln z , если z = ew , то

(Ln z)' = (e1w )' = e1w = 1z .

Пример 3.2 ([3], № 1.132). Найти постоянные a , b , c , при которых функция f ( z) будет аналитической:

1)f (z) = x + ay +i (bx +cy) ;

2)f ( z) = cos x (chy + ashy) +i sin x (chy +bshy) .

Решение.

1)	w = f (z) = u +iv = x + ay +i (bx +cy) ;			∂u =1	,	∂υ	= c с = 1,
				∂x		∂y
	∂u	= a ,	∂υ = b a = −b.
	∂y		∂x
Ответ: c =1 , a = −b .
2)	f (z) = u +iυ, u = cos x (chy + ashy) ;
	υ = sin x(chy	+bshy); ∂u = −sin x(chy +ashy) ;
			∂x

∂∂yυ = sin x(shy +bchy) a = −1 ; b = −1 .

При этом ∂∂uy = cos x(shy −chy) ; ∂∂υx = cos x(chy −shy) , т.е.

∂∂uy = −∂∂υx .

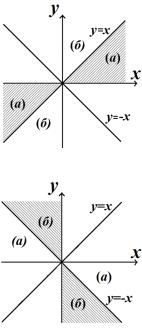
Пример 3.3 ([3], № 1.133). Найти области, в которых функция f (z) = x2 − y2 + 2i xy будет аналитической.

Решение. Рассмотрим два случая: 1) xy > 0 ; 2) xy < 0 .

В первом случае: а) x2 − y2 >0 ; б) x2 − y2 <0 (I и III четверти на рис. 3.1):

= −2y

∂υ ∂x

Рис. 3.1

Рис. 3.2

б) u = y2 − x2 ;

а) u = x2 − y		2 ; υ= 2xy ;		∂u = 2x ;
				∂x
	∂υ	= 2x	∂u	=	∂υ	;
	∂y		∂x		∂y
∂u	= −2 y;	∂υ =	2y		∂u	= −	∂υ.
∂y		∂x			∂y		∂x

Условия Коши–Римана выполняются.

б) u = y2 − x2 ; υ= 2xy ;	∂u	= −2x .
	∂x

Условия Коши–Римана не выполняются.

Во	втором	случае: а) х2	– у2	> 0,
б) x2 − y2 < 0		(II-я и IV-я четверти на рис.
3.2):			∂u
а)	u = x2 − y2 ; υ= −2xy ;		∂u	= 2x ;
			∂x

∂∂yυ = −2x , условия не выполняются.

υ= −2xy ;	∂u	= −2x ;	∂υ	= −2x ;	∂u	= 2 y ;
	∂x		∂y		∂y

, т.е. условия Коши–Римана выполняются.

Таким образом, функция аналитическая в областях:

3π

arg z

−π;−

−

;−

;

Пример 3.4 ([3], № 1.135). Пусть z = ρiφ , w = f ( z) =

=u(ρ,φ) +iυ(ρ,φ) . Записать уравнения Коши–Римана в полярных координатах.

x =ρcosϕ,	то
Решение. Так как	то
y =ρsin ϕ,

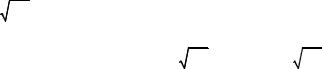
∂u = ∂u ∂x +

∂u ∂y

∂u cosφ

∂u sin φ,

∂ρ

∂x ∂ρ

∂y ∂ρ

∂x

∂y

∂υ

∂υ ∂x

∂υ ∂y

∂υ

(−ρsin φ) + ∂υρcos φ.

∂x ∂φ

∂y ∂φ

∂x

∂φ

∂y

Применяя условия Коши–Римана в переменных ( x, y) , получим

∂u

= ∂u cos φ+ ∂u sin φ;

∂ρ

∂x

∂y

∂υ

= ∂u

ρcosφ−

∂u ρsin φ

∂u = 1

∂υ

∂φ

∂x

∂y

∂ρ ρ ∂φ

Аналогично:

∂u = ∂u

∂x

∂u ∂y

∂u (−ρsin φ)

+ ∂u ρcosφ,

∂y ∂φ

∂φ

∂x ∂φ

∂x

∂y

∂υ

= ∂υ ∂x +

∂υ ∂y

∂υcosφ+

∂υsin φ.

∂ρ

∂x ∂ρ

∂y ∂ρ

∂x

∂y

По условиям Коши–Римана в переменных (x, y) :

∂u

= −

∂u ρsin φ+ ∂υρcos φ,

∂φ

∂x

∂y

∂u = −

∂υ .

∂υ

∂u cos φ+ ∂u sin φ

= −

ρ ∂φ

∂ρ

∂y

∂x

Таким образом, условия Коши–Римана в полярных координатах

имеют вид

∂u =

1 ∂υ

1 ∂u

= −

∂υ .

(3.2)

ρ ∂φ

∂ρ

Пример

3.5

([3],

№ 1.139).

Доказать,

что

для функции

f (z) =

в точке z = 0 выполняются условия Коши–Римана, но

производная не существует.

f ( z) =

u (x, y) =

Решение. Для функции

; υ = 0 ;

∂υ

= ∂υ = 0 всюду;

∂u

в точке z = 0 вычисляется как предел:

∂x

∂y

∂x

∂u

= lim

u (0 +

x,0) −u (0,0)

;

∂x

x=0

x→0

y=0

∂u

так как u (0 + x,0) = 0

и u (0,0) = 0

, то

= 0 .

∂x

x=0

Аналогично:

y=0

u (0 +

y,0) −u (0,0)

∂u

= lim

= 0 .

∂y

x=0

y→0

y=0

Таким образом, в этой точке условия Коши–Римана выполняются. Найдем производную в точке z = 0 , вычисляя предел по лучу y = k x . Тогда

lim	w	=	lim	x2k	,
	z			x (1 +ik )
z→0			x→0

откуда видно, что этот предел зависит от k, т.е. производной не существует.

Пример № 3.6 ([3], № 1.156). Будут ли гармоническими функ-

ции

f ( z)

, arg f (z) , ln

f (z)

, если

f (z) – аналитическая функция?

Решение. Рассмотрим функцию:

w =

f (z)

= u2 +υ2 =U +iV ,

где U = u2 +υ2 = Re w , V ≡ 0 = Im w ;

∂V

= ∂V

≡0 ;

∂U

∂u +

∂υ ;

∂x

∂y

∂x

2 +υ2

∂x

2 +υ2

∂x

u2 +υ2 ∂u −

∂u

∂2U

∂x

u2 +υ2

∂x

∂u

∂x2

u2 +υ2

∂x

u2 +υ2

∂υ −

υ2

∂υ

∂2u

∂2υ

∂x

2 +υ2

∂x

∂x2 +

∂x2

u2 +υ2

υ2

∂u 2

∂υ 2

u2 + υ2 (u2 + υ2 )

∂x

∂2u

∂2υ .

∂x2

u2 +υ2

Аналогично

u2 +υ2

∂x2

∂2U

υ2

∂u

∂υ

∂y

2 +υ2 (u2

+υ2 )

∂y

u2 +υ2 (u2 +υ2 )

∂y

∂2u

∂2υ;

∂y2

u2 + υ2

2 + υ2

∂y2

	U =	∂2U		+		∂2U	=
		∂x 2				∂y2

	u2				∂u 2
+							+
		3
	(u2 +υ2 )				∂x
			2

υ2

∂u

+ ∂u

)

∂x

∂y

+υ

∂υ 2

∂2u

∂y

∂x2

+υ

∂y2

∂2υ

∂u 2

≠ 0;

∂x

∂y

+υ

∂x

+υ

Таким образом, функция

f (z)

не является гармонической.

Рассмотрим функцию arg f (z) = arctg uυ +const .

∂(arg f (z))	=	1		∂
∂x	1	+	υ2	∂x
	1	+	u2
			u2

arg f (z) ,

где

f (z) = u( x, y) + iυ( x, y);

∂υ

−υ

∂u

∂υ

−υ

∂u

∂x

;

+υ

				∂υ		∂u
∂2 (arg f (z))	=	∂	u	∂x	−υ	∂x	=

∂x2				u2	+υ2
		∂x

(u2 +υ2) ∂u ∂υ+u

∂ υ2 −∂υ ∂u −υ

∂ u2 − u∂υ−υ∂u 2u ∂u +2υ∂υ

∂x ∂x

∂x ∂x ∂x

∂x

∂y

(u2 +υ2 )2

+υ

)

∂2υ

−υ

∂2u

−2

∂υ

−υ

∂u

+υ

∂υ

∂x

;

(u2 +υ2 )2

Аналогично

(u2 +

υ2 )

∂

∂u

∂υ

−υ

−2

∂υ −υ

+υ

∂2 (arg f (z))

∂y2

∂y

;

∂y2

(u2 +υ2 )2

arg f (z) =

∂2 (arg f (z))

∂x2

∂y2

∂2υ

∂

∂2u

∂x

∂y

∂x

∂y

−

u2 +υ2

(u2 +υ2 )2

× u ∂υ

−υ

∂u

u ∂u

+υ∂υ

+ u

∂υ

−υ

∂u

+υ

∂υ

∂x

∂y

∂u

=−

−u

−

−υ

+υ

(u2 +

υ2 )

∂y

∂x

∂y

∂x

∂y

∂x

(так

как

и,

υ –

гармонические

функции,

потому

∂2u

= 0 ,

∂x2

∂y

∂2υ

=0 , кроме того,

во втором слагаемом в силу условий

∂x2

∂y2

Коши–Римана мы заменили

∂υ

на −

∂u

∂υ

на

∂u

∂x

∂y

∂x

2 ∂u

∂u

∂u 2

(arg f (z)) = −

−u

+uυ

−uυ

(u2

+υ2 )

∂x

∂y

∂x

+υ

2 ∂u

∂u

2 ∂u

∂u

∂u 2

∂u

= 0.

∂x

∂y

∂x

∂y

+uυ

−uυ

∂y

−υ

∂x

∂y

Таким образом, функция arg f (z)

является гармонической (при

условии аналитичности функции f (z) ).

Можно было бы сделать этот пример и иначе, но для этого предварительно докажем еще одну форму записи условий Коши–

Римана, а именно: если функция

w = f (x, y)

записана в виде

w = R(x, y) eiΦ( x, y) , где

R(x, y) =

а Φ(x, y) =arg w ,

то условия

Коши–Римана можно записать в виде:

∂R

= R ∂Φ,

∂R

= −R

∂Φ,

(3.3)

∂x

∂y

∂x

Действительно:

w = u(x, y) +iυ( x, y) = R (x, y)eiΦ( x, y) = R cos Φ +iR sin Φ ,

т.е.

u(x, y) = R( x, y)cos Φ( x, y) ,

υ( x, y) = R ( x, y)sin Φ( x, y) .

Используя условия Коши–Римана

∂u =

∂υ ,

∂u

= −∂υ

, получим

∂x

∂y

∂x

∂R

∂Φ

∂R

∂Φ

∂x cos Φ− Rsin Φ

∂x

= ∂y sin Φ+ RcosΦ ∂y

∂R

∂Φ

∂R

∂Φ

∂y cos Φ− Rsin Φ

∂y

= −

∂x sin Φ− RcosΦ ∂x .

Умножим первое уравнение на cos Φ , а второе – на sin Φ и сложим:

∂∂Rx = R ∂Φ∂y .

Второе условие получим, умножив первое уравнение наsin Φ , а второе – на cos Φ :

∂∂Ry = −R ∂Φ∂x .

Пользуясь уравнениями (3.3), докажем полученные ранее результаты относительно гармоничности функций arg f (z), f (z) ,

ln f (z) . Так как arg f (z) = Φ(x, y) в принятых здесь обозначениях,

то дифференцируя первое из равенств (3.3) по у, а второе – по х и вычитая их, получим:

∂R	∂Φ	+ R	∂2Φ	+	∂R	∂Φ	+ R	∂2Φ	= 0 .
∂y	∂y		∂y2		∂x	∂x		∂x2

В силу (3.3) первое и третье слагаемые уничтожаются, что при-

водит к уравнению ∂2Φ + ∂2Φ = 0 , из которого следует гармонич-

∂x2 ∂y2

ность функции Ф(х,у).

Аналогично для функции | f (x, y) |= R(x, y) продифференцируем первое из уравнений (3.3) по х, а второе – по у и сложим:

∂2 R

= ∂R

∂Φ + R

∂2Φ

−

∂R

∂Φ − R

∂2Φ

;

∂x2

∂y2

∂x∂y

∂x

∂y

∂x

R =

∂2 R

∂R

∂Φ −

∂R

∂Φ .

∂x2

∂y2

∂y

∂x

∂y

В силу (3.3) правая часть приобретает вид:

−R ∂Φ∂ 2 −

	∂Φ 2
R		= −R
∂y
∂y

∂Φ 2		∂Φ 2	≠ 0,
	+		≠ 0,
∂x	∂y
∂x	∂y

следовательно, R ≠ 0 и функция

f (x, y)

не является гармониче-

ской.

f (x, y)

И, наконец, для функции ln

получим

∂R

∂

(ln

f (x, y)

)

∂

(ln R(x, y)) =

∂x ,

∂x

∂

(ln

f ( x, y)

)

∂

(ln R(x, y)) =

∂R

∂y .

∂y

<<< < Предыдущая 1 2 34 / 254 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
12.11.20226.39 Mб3Международная телекоммуникатсионная конферентсия Молодеж и наука Ч.2 2015.pdf
#
12.11.20224.22 Mб3Международная телекоммуникатсионная конферентсия Молодеж и наука Ч.3 2015.pdf
#
12.11.20225.39 Mб25Миленин Обучение комплексу базовыкх боевыкх приемов самбо 2015.pdf
#
12.11.20221.05 Mб10Милославская сетевые атаки на открытые системы на примере 2012.pdf
#
12.11.20224.57 Mб9Мискевич Прямое преобразование ядерной енергии 2011.pdf
#
12.11.20223.91 Mб6Михайлов ТФКП Практикум 2013.pdf
#
12.11.2022608.01 Кб4Михеев Лабораторный практикум Специалные вопросы 2012.pdf
#
12.11.20222.39 Mб4Михеев Теоретические основы специалности Елементная база автоматических систем Лабораторный практикум 2012.pdf
#
12.11.20223.86 Mб6Мишулина Основы теории вероятностей 2011.pdf
#
12.11.20221.45 Mб7Мкртчян Учебное пособие по русскому языку как иностранному для спетсиалности 2015.pdf
#
12.11.2022966.07 Кб4Молошная Електромагнитная совместимост.pdf