Михайлов ТФКП Практикум 2013

Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный исследовательский ядерный университет (МИФИ)

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

1 x1−p (1− x)p

му берегу разреза ∫0

dx = J (искомый). На нижнем бере-

гу z1− p = e(1− p )(ln x) = x1− p ; (1− z)p

−2πi) = e−2 pπi (1− x)p . Поэтому

.pdf

Скачиваний:

Добавлен:

12.11.2022

Размер:

3.91 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 1920 / 2520 21 22 23 24 25 > Следующая >>>

∞ x2dx

2πi

+ πi

z 2

+ πi

∫0 x4 −1

4z3

z=i

z=−1

−

πi

= z=1

Пр имер 13.9 ([3], № 4.178). Вычислить главное значение инте-

грала ∞∫	x pdx	; (−1 < p < 0).
грала ∞∫	1− x	; (−1 < p < 0).
0	1− x		z pdz
Решение.		Рассмотрим ∫	z pdz	по контуру С, представленному
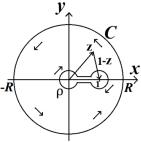
Решение.		Рассмотрим ∫		по контуру С, представленному
		C	1− z

на рис. 13.5. Внутри контура функция аналитическая. Поэтому интеграл по всему контуру С равен 0. В то же время его можно расписать как состоящим из интегралов по составным частям контура. Интегралы по малой дуге радиуса ρ1 с центром в начале координат и по большой дуге радиуса R при стремлении ρ1 →0 и R →∞ , со-

ответственно, как легко показывается, обращаются в 0 (см. пример

13.6 и др.).

Интеграл по верхней полуокружности
радиуса ρ2 с центром в точке z = 1 при
стремлении ρ	2	→0	равен −πi res			[	f (z),1 ,
	2					[	]
так как точка z = 1			– полюс первого по-
рядка, то				z p
−πi res[f (z),1]= −πi				z p		= πi .
−πi res[f (z),1]= −πi				−1	z=1	= πi .		Рис. 13.5
				−1

Интеграл по нижней полуокружности
Интеграл по нижней полуокружности
равен πie2 πip . Множитель e2iπp					появляется из-за перехода на дру-

гую ветвь функции zр при переходе с верхнего берега разреза на нижний. Главное значение интеграла по верхнему берегу действительной положительной полуоси равно вычисляемому интегралу:

J = ∞∫	x p dx	.

0	1− x

Интеграл по нижнему берегу действительной положительной полуоси дает

191

p(ln x+iπ)

∞

∫ e

dx = e2iπp ∫

= −e2iπp ∫

= −e2iπp J .

∞

1− x

∞

1− x

0 1− x

Таким образом, получаем:

J −e2iπp J + πi(1+e2iπp ) = 0

J =

−πi(1+e2iπp )

−πi(1+e2iπp )(1−e−2iπp )

1−e2iπp

(1−e2iπp )(1−e−2iπp )

−πi(e2iπp

−e−2iπp )

πi 2isin 2πp

2πsin 2πp

= πctgπp .

= −

2 −(e2iπp

+e−2iπp )

2 −2cos 2πp

2 2sin2 πp

Пример 13.10 ([3], № 4.179). Вычислить главное значение инте-

+∞	e	px	dxx	(0 < p <1) .
грала ∫
−∞	1	−e

Решение. Сводится к предыдущему примеру заменой ex = t .

Пример 13.11 ([3], № 4.180). Вычислить интеграл

1 1−p			(1− x)	p
J = ∫	x		(1− x)		dx ;	(−1 < p < 2).
J = ∫			3		dx ;	(−1 < p < 2).
0		(1+ x)
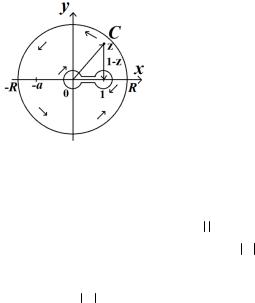
Решение. Рассмотрим интеграл ∫						z1−p (1− z)p	dz	, где С – контур,
Решение. Рассмотрим интеграл ∫						3	dz	, где С – контур,
					C	(1+ z)

представленный на рис. 13.6. Выделим в подынтегральной функции интегрируемую ветвь, являющуюся аналитическим продолжением с действительной оси (ее верхнего берега) функции

x1−p (1− x)p .

По

определению z1− p = e(1− p )Lnz и

(1− z)p = epLn(1−z) ,

z1−p = e(1−p)(ln

+iφ+2πki) .

На действительной оси

= x ; φ = 0 и

z1− p = e(1− p )(lnx +2 πki )

= e(1− p ) ln x = x1− p при k = 0.

Таким образом, интегрируем ветвь

Рис. 13.6

z1−p = e(1−p)(ln

+iφ) .

192

Аналогично, (1− z)p = epLn(1−z) = ep(ln 1−z +iarg(1−z)+2πki) .

На действительной

оси ln

1− z

= ln

1− x

arg (1− z)= 0 (при

0 < z <1 ) k = 0 .

(1− z)p = ep(ln

+iarg(1−z)).

Интегрируем ветвь

1−z

Внутри контура у

подынтегральной функции есть одна особая точка z = −1 – полюс третьего порядка. Вычислим вычет в этой точке:

res[f (z),−1]=

lim

f (z) (1+ z)3

lim

(z1−p (1−z)p )=

2!z→−1 dz

=1 lim[−p(1− p) z−1−p (1− z)p −(1− p)pz− p (1− z)p−1 −

2 z→−1

−(1− p)pz− p (1− z)p−1 + p(p −1)z1−p (1− z)p−2 ] .

Здесь для выделения ветвей

z1−p		= ei(1−p)π ,	(1− z)p	= ep(ln 2) = 2p
	z=−1			z=−1

(так как arg (1− z)		остался равным 0). Следовательно:

res[f (z), −1]= 12 [−p(1− p)ei(1−p)π 2p +(1− p)pei(1−p)π 2p−1 +

+(1− p)pei(1−p)π 2p−1 + p(p −1)ei(1−p)π 2p−2 ] =

[ p2 − p +

(1− p)p

p(p −1)

iπ 1−p

] = e

(

) 2 p−1

−

= 18 eiπ(1−p) 2p p(p −1).

Вычислим интегралы по составным частям контура. По верхне-

интеграл по нижнему берегу разреза равен

193

∫ x

(1− x)

dx = −∫ x

(1− x)

dx = −e−2 pπi J .

3 e

−2 pπi

3 e

1−p

−2 pπi

(1+ x)

Оценим интегралы по окружностям. Интеграл по малой окружности радиуса ρ с центром в начале координат, где z = ρeiφ :

z1−p (1− z)p

2π ρ1−p

1−ρeiφ

2π ρ2−p

1−ρeiφ

∫

≤ ∫

ρdφ =∫

dφ→0

(1+ z)

+ρeiφ

1+ρeiφ

Cρ

при

ρ → 0 , так как p < 2 . Интеграл по малой окружности радиуса

ρ с центром в точке z =1 , где 1− z = ρeiφ; dz = −ρieiφdφ; z =1−ρeiφ :

1−p

(1− z)

2π

(1−ρeiφ )1−p

ρp

∫

≤ ∫

ρdφ =

(1+ z)

2 −ρeiφ

Cρ'

2π

1−ρeiφ

1−p

=ρp+1

∫

dφ→0 ,

2 −ρeiφ

так как

p > −1 .

Интеграл по большой окружности радиуса R, где

z = Reiφ :

z1−p (1− z)p

2π R1−p

1− Reiφ

∫

≤

∫

Rdφ≤

const → 0

(1+ z)

1+ Reiφ

при R →∞ . Таким образом, имеем

J −e−2iπp J =

2πi ei(1−p)π 2p p( p −1);

2p p( p −1)

J =

πi

eiπ e−ipπ

1−e−2πpi

= −

πi

p( p −1)

e−iπp (1−e2πpi )

−e−2πpi )(1−e2πpi )

= −

πi

2p p

( p −1)

e−πpi −eπpi

2 −(e2πpi +e−2πpi )

194

= −	πi	2p p(p −1)	−2isin πp	= −	πi	2p p(p −1)	−	i	=
	4		2 −2cos 2πp		4
								2sin πp

=π p (1 − p)2 p . 8 sin πp

Пример 13.12 ([3], № 4.181). Вычислить интеграл

1	x1−p (1− x)p			(−1 < p < 2).
∫			dx ;
	1+ x	2
0

Решение. Рассмотрим интеграл по тому же контуру С, что и в примере 13.11. Ветвящиеся функции те же самые, поэтому воспользуемся некоторыми результатами этого примера. Внутри контура С теперь две особые точки ±i с полюсом первого порядка в

них. Вычеты вычислим по формуле ψφ' , где φ(z) = z1−p (1− z)p ;

ψ(z) =1+ z2 . Ветви выделены те же, что и в примере 13.11. В точке z = i :

z1−p

= e(1−p)i

= ei

e−i π2 p = ie−i π2 p ;

z=i

p ln 2 −i π

(1− z)

−i

;

= e

4 = 2 2 e

z=i

−i

res[f (z),i]=

ie 2

2 2

= 2

−1

e−i

3π

p .

В точке z = −i

z1−p

(1−p)i

3π

−i

3π

= e

2 = −ie

;

(1− z)

z=−i

p ln 2

;

= e

4 = 2 2 e

z=−i

−i

3π

5π

res[f (z), −i]=

−ie 2

2 2

e 4 = 2

−1

e−i

p .

−2i

195

Интеграл по всему составному контуру равен:

−1

−i 5π p

−1

−i

3π p

−i

5π p

−i

3π p

2πi

2 2

+ 2 2

= πi 2 2 e

Вычислим интегралы по составным частям контура. Интеграл по верхнему берегу разреза равен J (искомый), по нижнему берегу −e−2πpi J (см. пример 13.11). Интегралы по малым окружностям обращаются в ноль при стремлении радиусов к нулю. Остается вычислить интеграл по большой окружности, который в данном случае в нуль не обращается (недостаточная степень убывания модуля подынтегральной функции при R →∞ ):

	∫	z1−p (1− z)p	dz = −2πires[f (z),∞].
		1+ z2
	CR
В точке z =∞		f (z) имеет разложение в ряд Лорана,			начинаю-
щееся с члена	c	, так как главный член имеет вид		(−1)p	. Для вы-
	−1			z
числения (−1)p	z
	возьмем произвольную, удаленную от начала коор-

динат точку, например, на действительной положительной полуоси. Тогда

z1−p

= x1−p ;

(1− z)p = epLn(1−z) = ep(ln

1−x

−iπ) = e−iπp

1− x

(пользуемся выделенной

ранее

ветвью).

Таким образом, при

x → +∞

z1−p (1 − z )p

x1−p (x −1)p e−iπp

e−iπp

1+ z2

1 + x2

или

z1−p (1 − z)p

e−iπp

1+ z2

(для любых z →∞ , так как z =∞ правильная точка подынтегральной функции). Следовательно,

res[f (z),∞]= −c−1 = −e−iπp .

196

Интеграл по большой окружности, таким образом, равен

−2πires[f (z),∞]= 2πie−iπp .

Приравняем интеграл, вычисленный по составным частям контура, интегралу, вычисленному с помощью вычетов:

−i 5π p

−i 3π p

J (1−e−2iπp )+ 2πie−iπp = πi 2 2

−i 5π p

−i 3π p

πi 2 2

−2πie−iπp

J =

1−e−2iπp

−i 5π p

−i

3π p

−2e−iπp

−e2iπp )

πi 2 2

(

)(

)

1−e−2iπp

1−e2iπp

−i 5π p

−i 3π p

5π p

i 3π p

2eiπp

πi

2 2

−2e−iπp −2 2

2 −2cos 2πp

(e−

5πpi

(e−

3πpi

) + 2(eiπp −e−iπp )]

πi[2

−e

) + 2

−e

2(1 −cos 2πp)

πi[−2

2i sin 5πpi −2

2isin

3πpi

+4isin πp]

2 2sin2

πp

πi[4isin πp −2i 2

5πpi +sin

3πpi )]

(sin

4sin2 πp

πp

−π(2sin πp −2

2sin πp cos

)

π(2

cos

−1)

2sin

2 πp

sin πp

197

Пример 13.13 ([3], № 4.183). Вычислить интеграл

∫1 (	x	) p	dx	(−1	< p <1; a > 0).
	1− x		x +a
0
Решение. Рассмотрим интеграл					∫(	z	)p	dz	по контуру С,
						−z		z +a
					C 1

представленному на рисунке 13.7. Составной контур С ограничивает двусвязную область извне окружностью с центром в начале координат достаточно большого радиуса R и изнутри окружностями малого радиуса ρ

сцентром в начале координат и с центром

вточке z =1 (точки ветвления подынтегральной функции), соединенными между собой верхним и нижним берегами разреза по действительной оси ρ < x < 1 – ρ. Ветвь, как обычно, выделяем условием


Рис. 13.7			аналитического продолжения подынте-
Рис. 13.7			гральной функции с верхнего берега раз-
			гральной функции с верхнего берега раз-
реза (0 < x <1) . Функция z p				= e pLnz = e p (ln	z	+i arg z +i 2 πk ) . На верхнем бе-


регу разреза	z	= x ; arg z = 0		и x p = e p (ln x +i 2 πk ) k = 0; следователь-
регу разреза	z	= x ; arg z = 0		и x p = e p (ln x +i 2 πk ) k = 0; следователь-

но, интегрируется ветвь zp =ep(ln z +i arg z) .

Аналогично функция (1−z)p =ep(ln1−z +i arg(1−z)+i2πk) на верхнем берегу равна (1− x) p = ep(ln(1−x)+i 0+i2πk ) k = 0. Интегрируется ветвь (1− z) p = ep(ln 1−z +i arg(1−z)) . Внутри контура выделенная однозначная аналитическая ветвь имеет одну особую точку z = −a (полюс пер-

вого порядка).			Вычислим вычет в этой точке по формуле ϕ/ψ′ , где
	z p		ψ( z) = z + a. В точке z = −a функция
φ(z) =		,

	1− z

z p =ep(ln		z	+i arg z)		z=−a	=ep(ln a+iπ) = ap eiπp ,



а функция
(1− z) p = e p(ln	1−z			+i arg(1−z))			= e p(ln(1+a)+i 0) = (1 + a) p .



							z=−a
							z=−a

198

Интеграл равен

C∫	z p	dz		a peiπp
			= 2πi res[ f (z), −a] = 2πi			.
		z +a		(1+a)	p
	1− z

Вычислим этот же интеграл по составным частям контура С. Покажем, что интегралы по малым окружностям обращаются в 0

при ρ → 0. На окружности с центром в начале координат z = ρeiφ; dz = ρieiφdφ,

(ρeiφ) p

ρieiφdφ

2π

ρp ρdφ

p+1

∫

≤ ∫

= ρ

const → 0

(1−ρe

iφ

)

ρe

iφ

+ a

1−ρe

iφ

ρe

iφ

+ a

Cρ

при ρ → 0 , так как p > −1.

Аналогично оценивается интеграл по малой окружности с центром в точке z = 1. Вычислим интеграл по большой окружности, на

Функция на бесконечности имеет правильную точку, ее предел в бесконечности равен 0 по любому направлению. Для простоты рассмотрим предел по действительной положительной полуоси:

z p

iπp

f (z) =

z +a

(x −1)

−iπp

1− z

z=x

+a x~→∞

eiπp

= eiπp и ин-

То есть главный член функции имеет вид

−1

теграл равен

−2πi (−c−1) = 2πieiπp .

Интеграл по верхнему берегу есть искомый интеграл J. Осталось рассмотреть интеграл по нижнему берегу разреза. Здесь

z p = x p ; (1−z)p =ep(ln1−z −2iπ) =e−2πpi (1−x)p.

Таким образом, интеграл по нижнему берегу при ρ → 0 равен

e2πpi 0∫	x	p	dx	= −e2πpi J .
			x +a
1	1− x

199

2 πpi

Приравняв интегралы, вычисленные разными способами, получим:

J −e2πpi J + 2πieiπp = 2πi

a p

eiπp

+ a) p

2πi[(

) p −1] eiπp

2πi eiπp [(

) p −1] (1−e−2πpi )

+ a

J =

1−e2πpi

(1−e2πpi )(1−e−2πpi )

2πi[(

−1] 2isin πp

[1−(

] 2π sin πp

2 −2cos 2πp

1−cos 2πp

[1−

sin πp

(

)

]

= 2π [1−

1+ a

(

)

]

= π

1+a

2sin2 πp

sin πp

Пример 13.14 ([3], № 4.184). Вычислить интеграл

∫0 (

)

(−1

< p <1, a > 0).

1− x

(x +a)2

Решение. Рассмотрим этот интеграл по контуру С, как и в при-

мере 13.13, только интеграл по большой окружности при R →∞ обращается в 0 (более высокая степень убывания функции на бесконечности, чем первая).

Точка z = −a теперь будет полюсом не первого, а второго порядка. Вычет в точке z = −a вычисляем по формуле

res[ f (z), −a] = lim

(

) p = p(

) p−1

− z

− z)2

z→−a dz 1

z=−a

= −peπpi

a p−1

(a +1) p+1

Интеграл равен

2πi res[ f (z), −a] = −2πipeπpi

a p−1

(a +1)p+1

Интегралы по большой и малой окружностям в пределе обращаются в 0, а интеграл по нижнему берегу разреза равен −e J (см. предыдущий пример). Получаем равенство:

200

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 1920 / 2520 21 22 23 24 25 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
12.11.20226.39 Mб3Международная телекоммуникатсионная конферентсия Молодеж и наука Ч.2 2015.pdf
#
12.11.20224.22 Mб3Международная телекоммуникатсионная конферентсия Молодеж и наука Ч.3 2015.pdf
#
12.11.20225.39 Mб25Миленин Обучение комплексу базовыкх боевыкх приемов самбо 2015.pdf
#
12.11.20221.05 Mб10Милославская сетевые атаки на открытые системы на примере 2012.pdf
#
12.11.20224.57 Mб9Мискевич Прямое преобразование ядерной енергии 2011.pdf
#
12.11.20223.91 Mб6Михайлов ТФКП Практикум 2013.pdf
#
12.11.2022608.01 Кб4Михеев Лабораторный практикум Специалные вопросы 2012.pdf
#
12.11.20222.39 Mб4Михеев Теоретические основы специалности Елементная база автоматических систем Лабораторный практикум 2012.pdf
#
12.11.20223.86 Mб6Мишулина Основы теории вероятностей 2011.pdf
#
12.11.20221.45 Mб7Мкртчян Учебное пособие по русскому языку как иностранному для спетсиалности 2015.pdf
#
12.11.2022966.07 Кб4Молошная Електромагнитная совместимост.pdf