Круглов Руководство по технической термодинамике 2012

Приложение

РЕШЕНИЯ И ОТВЕТЫ

П.1. Основные понятия и законы термодинамики

П. 1.1. a. αp =1/ T ; βT =1 / p ; γV = 1/ T .

б. αp = T1 (1 + b / (V − b) − 2a(V − b) / (V 2RT))−1 ;

βT = (VRT / (V − b)2 − 2a / V 2)−1 ; γV = R / ( p(V − b)) .

Указание: при выводе выражения для αр воспользоваться уравнением состояния ТС в частных производных:

∂∂Vp T ∂∂VT p ∂∂Tp V = −1 .

П. 1.2. а) Ограничиваясь линейным приближением для вариации удельной теплоты δq и учитывая, что вариации независимых переменных можно приравнять их дифференциалам, получим:

Из сопоставления полученного выражения с выражением, приведенным в условии задачи, следует, что

A = (∂q / ∂T)v ≡ cv – удельная теплоемкость при постоянном объеме;

B = (∂q / ∂v)T ≡ λv – скрытая теплота изотермического изменения объема;

C = (∂q / ∂T) p ≡ cp – удельная теплоемкость при постоянном давлении;

D = (∂q / ∂p)T ≡ λp – скрытая теплота изотермического изменения давления.

121

б) Используя правую часть полученного в п. (а) выражения и выражая производные через термодинамические коэффициенты

cv, cp, λv, λp , получим

cpdTp = cvdTp + λvdvp при p = const.

Отсюда непосредственно следуют необходимые соотношения.

П.1.3. Полученные в задаче 1.3 выражения для элементарного приращения теплоты в случае адиабатических условий имеют вид

где индекс S обозначает адиабатичность условий. Отсюда следует, что

Из соотношения, полученного в п. (б) задачи 1.2, следует, что

Выразив левые части выражений (П.1.1) и (П.1.2) через термодинамические коэффициенты βS и βT и поделив их друг на друга, получим необходимое соотношение.

П.1.4. а) Используя выражение, приведенное в условиях задачи 1.3 (п. (б)), и уравнение состояния дли одного моля идеального газа pV = RТ, нетрудно получить λV = p; λp = −V.

б) Взяв за исходное то же выражение, что и при решении п. (а) и определив из уравнении состояния Ван-дер-Ваальса (p = RT/(V – b) – a/V2) производные ( ∂p/ ∂T)V и ( ∂V/ ∂T)p, нетрудно получить

λp ≈ −(V − b)(1 + 2a / (RTV)) ;

λV ≈ 2a(VV 3− b) − VRT− b 1 + RTV2a .

122

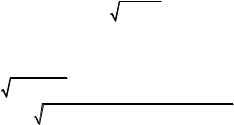
П.1.5. С учетом определения термодинамического коэффициента сжимаемости, приведенного в задаче 1.1, и выражения, связывающего изотермический и адиабатический коэффициенты сжимаемости (см. условия задачи 1.4), модуль всестороннего сжатия можно представить в виде

последнюю формулу значения изотермических коэффициентов сжимаемости для идеального газа и газа Ван-дер-Ваальса, полученные в задаче 1.2, будем окончательно иметь:

а) идеальный газ wзв = (RTk/M) ;

б) газ Ван-дер-Ваальса wзв = kV (VRT /(V − b)2 − 2a / V −2)/ M . M и V – молекулярная масса и молекулярный объем газа.

П.1.6. При отсутствии сил молекулярного притяжения уравнение Ван-дер-Ваальса принимает вид p = RT/(V – b) и тогда z = V/(V – b).

Сравнивая полученное значение z со значением, заданным в условиях задачи, получим

При η → 0 коэффициент b = 4πd3/6. С увеличением концентрации частиц величина коэффициента b уменьшается.

П.1.7.Система уравнений, описывающая движение двух связанных осцилляторов, имеет вид:

х2 – отклонения молекул из положения равновесия; γ – силовая константа взаимодействия молекул, которая в случае характерного для газа Ван-дер-Ваальса диполь-дипольного взаимодействия рав-

на γ = е2/(4πε0r3). Принимая, что решение имеет вид хк = аkеiωt, и

123

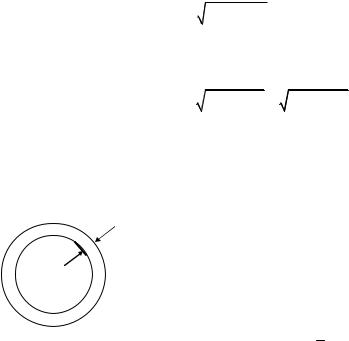
подставляя его в написанную выше систему уравнений, получим характеристическое уравнение

(ω02 − ω2 )2 = γ2 /m2.

Отсюда частоты обобщенных колебаний равны

ω1,2 = ω02 ± γ / m.

Представляя энергию взаимодействия в виде разности энергий взаимодействующих и невзаимодействующих осцилляторов, получим

Здесь С – постоянная молекулярного взаимодействия.

П.1.9. Указание: использовать для δQ выражения, полученные в задаче 1.3:

δQ = CvdT + λvdV =CpdT + λpdp .

П.1.10. В политропном процессе

δQ = CdT = CvdT + λvdV =CpdT + λpdp ,

где С = const. Отсюда следует, что

124

и отсюда следует pV n = const (уравнение политропного процесса для идеального газа). Теплоемкость в политропном процессе

где k = Cp/Cv.

Из последнего выражения видно, что если показатель политропы изменяется в пределах от 1 до k, то теплоемкость отрицательна. Для изобарического процесса С = Cv и n → ∞; для изотермического процесса n = 1 и С → ∞; для адиабатического процесса n = k и

С = 0.

П.1.11. В случае идеального газа pV = RT, U = U0(T), и тогда имеем

∫ δQ = ∫ dU + pdV = ∫ dU 0(T) + ∫ dV = v T v T v T Rv V 0 ,

так как каждое из слагаемых по отдельности равно нулю (вследствие равенства нулю интеграла от функции одной переменной по замкнутому контуру).

В случае газа Ван-дер-Ваальса

при условии СV = СV(T), λV= A(V)T или Сp = Сp(T), λp= B(p)T. Доказательство аналогично доказательству, приведенному в задаче 1.11.

125

П.1.13. а) Для нахождения разности Сp – СV можно воспользоваться соотношениями, приведенными в условии задачи 1.3, и первым началом термодинамики:

Для моля идеального газа pV = RT, U = U0(T). Отсюда получим, используя выражение (П.1.3):

Cp −CV = pR/ p = R .

Для моля газа Ван-дер-Ваальса

Отсюда находим, используя выражение (П.1.3):

Cp −CV = R (1−2a(V −b)2 / RTV 3)−1 .

б) Воспользовавшись основным уравнением термодинамики и выражением для элементарного количества теплоты, приведенным в задаче 1.3:

TdS =δQ ; δQ = CV dT +λV dV,

нетрудно получить

S = S(T, V) − S(T 0 , V0) = T∫ CVTdT + V∫ λVTdV .

T0 V0

Для идеального газа СV = const, λV = p. Откуда находим

S = CV ln(T /T0) + R ln(V / V0) = R ln ((T /T0)CV /R(V /V0)).

Для газа Ван-дер-Ваальса

λV = RT / (V −b), CV ≠ f (T)

и, следовательно,

S = R ln ((T / T0)CV /R(V −b) / (V0 −b)).

в) Для адиабатического процесса S = 0, и тогда из п. (б) следует, что для идеального газа уравнение адиабаты имеет вид:

T (CV /R)V = const или T (1/k−1)V = const ,

где k = Cp/CV. Переходя с помощью уравнения состояния к координатам p, V, получим: pVk = const.

126

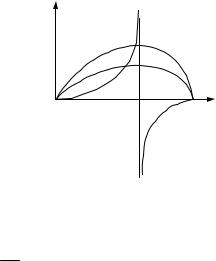
Аналогичным образом можно получить для газа Ван-дер- Ваальса

П.1.14. Воспользовавшись приближенной формулой Стирлинга ln(N!) ≈ NlnN – N, представим энтропию в виде

S = − kБN( p1 ln p1 + p2 ln p2) .

Учитывая, что p1 + p2 = 1, выразим S через u и ε1, ε2:

где u = U/N – средняя внутренняя энергия, приходящаяся на одну частицу.

При V = const сохраняются неизменными энергетические уровни ε1 и ε2. Температура определяется соотношением:

П.1.15. Воспользовавшись для Cp – CV соотношением, приведенным в условиях задачи 1.3, и учитывая, что λV = T(∂p/∂T)V, получим:

C p −Cv = λV ∂∂VT p = T ∂∂Tp V ∂∂VT p = pVTγV αp .

127

Выразив γV через αp и βT c помощью уравнения состояния газоподобной системы в термодинамических коэффициентах αp = pβTγV, приходим к выражению

Cp −Cv =VTα2p / βT .

П.1.16. Выражая с помощью основного уравнения равновесной термодинамики термодинамические коэффициенты αp, βT, γV, λV, λp, CV и Cp, через частные производные энтропии получим:

Применяя к полученным соотношениям третье начало термодинамики, нетрудно убедится, что все они, кроме βT, стремятся к нулю при Т → ∞.

П.1.17. Для парамагнетика основное уравнение термодинамики имеет вид

где М – величина вектора намагниченности, а H − напряженность магнитного поля.

В соответствии с законом Кюри M = χH = cH/T (c = const). Из

Аналогичным образом при p = const имеем

128

2 2

∫(dQ)p = ∫d(U + pV) = H2 − H1 ,

1 1

где H = U + pV – энтальпия, являющаяся так же, как и внутренняя энергия, функцией состояния.

П.1.19. Из основного уравнения термодинамики следует, что

Поскольку энтропия является функцией состояния и обладает свойством потенциальности, то выполняются следующие условия:

lV = p. С учетом условия pV = f (T) получим уравнение для нахождения функции f(T):

T d f (T ) − f (T ) = 0 . dT

Интегрируя это уравнение, имеем f (T) = RT. Постоянная интегрирования R не зависит от температуры и объема и для одного моля идеального газа равна универсальной газовой постоянной:

R = 8,314 Дж/(моль К).

циала имеем

129

Если p является линейной функцией Т (как, например, для идеаль-

ного газа или газа Ван-дер-Ваальса), то ∂∂CVV T = 0 .

2. Методы термодинамического анализа

П.2.1.а) dH = TdS + Vdp + ∑μidNi ;

i

dF = − SdT − pdV + ∑μidNi ;

i

dФ = − SdT + Vdp + ∑μidNi .

i

б) Выражения для элементарных приращений этих функций d(pV) и d(TS):

Они действительно являются полными дифференциалами (а сами функции потенциалами), так как их смешанные вторые производные равны между собой:

в) Соотношения Максвелла можно получить, приравнивая друг к другу смешанные производные для каждой потенциальной функции.

г) Рассматривая химический потенциал как функцию интенсивных переменных p и T:

130