
- •2.2. Оптимальное распределение нагрузки
- •Математически задача в этом случае формулируется следующим образом: найти
- •при ограничениях
- •Введя новые переменные
- •запишем задачу (2.88) в виде: найти
- •при ограничениях
- •Рис. 2.8. Решение оптимизационной задачи для системы двух реакторов
- •с нелинейной зависимостью степени снижения мощности от запаса реактивности
- •Условие совпадения углового коэффициента касательной с угловым коэффициентом целевой функции есть:
- •откуда
- •Используя полученное соотношение (2.90) и условие связи между переменными
- •получим оптимальное распределение относительных запасов реактивности
- •Используя (2.91), получим, что
- •Таким образом, решением задачи при параметре системы F > 1 является
- •Решением задачи при параметре системы F < 1 будут
- •Если параметр системы равен единице, то оптимальным является распределение
- •Из выражений (2.93), (2.94) легко видеть, что
- •На рис. 2.9 показаны фазовые диаграммы оптимального распределения запасов реактивности.
- •Рис. 2.9. Траектории оптимальных распределений запасов реактивности
- •в системе двух реакторов с нелинейной зависимостью
- •Используя выражения для оптимальных распределений запасов реактивности, можно получить оптимальное распределение степеней снижения мощностей реакторов с учетом того, что
- •Оптимальное распределение степеней снижения мощностей реакторов есть:
- •1) параметр системы F > 1
- •2) параметр системы F < 1
- •3) параметр системы F = 1
- •Рис. 2.10. Траектории оптимальных степеней снижения мощности
- •в системе двух реакторов с нелинейной зависимостью
- •Оптимальные режимы эксплуатации системы двух реакторов
- •параметра системы
- •Оптимальные
- •траектории
- •Оптимальные
- •режимы
- •базисный
- •2.2.3. Максимально возможный эффект оптимизации
- •Результаты расчетов для конкретного случая, когда доли мощности реакторов одинаковы, приведены на рис. 2.11.
- •Как видно из рисунка, оптимизация дает тем больший эффект, чем больше параметр системы F отличается от единицы. Оптимизация системы наиболее существенна в области снижения мощности АЭС со 100 до 20 % номинальной.
- •Полученные результаты для реакторов с нелинейной зависимостью сводятся к следующим выводам.
- •Характер оптимальных распределений запасов реактивности и оптимальных степеней снижения мощности определяется величиной параметра системы
- •Оптимальный режим эксплуатации реакторов может быть двух типов при F ≠ 1 и одного типа при F = 1.
- •Например, из решения оптимизационной задачи для двух реакторов типа РБМК, следует что оптимальным является равномерное снижение мощности, а «антиоптимальным» – отработка переменного графика одним блоком.
- •В целом, решение задачи по оптимизации распределения запасов реактивности в системе реакторов позволяет сделать следующие выводы.
- •2. Возможный проигрыш от пренебрежения оптимизацией наиболее существенен в предполагаемом регулировочном диапазоне работы АЭС. Величина эффекта оптимизации тем больше, чем больше параметр системы отличается от единицы.

резервируется запас реактивности на полную остановку (за исключением случая, когда требуемая степень снижения мощности АЭС равна нулю). Это объясняется тем, что запас реактивности, обеспечивающий заданную степень снижения мощности реактора, резко увеличивается при ε → 0 , что, в свою очередь, приводит к увеличению потери энерговыработки.
2.2.3. Максимально возможный эффект оптимизации
Об эффективности оптимизации будем судить по величине:
S(α) = Smax − Smin ,
∑N ϕi i=1 ai
где Smax и Smin – максимальная и минимальная потеря энерговы-
N |
ϕ |
i – потеря |
работки АЭС при степени снижения мощности α ; ∑ |
|
i=1 ai
энерговыработки АЭС при резервировании запаса реактивности на полную остановку реакторов.
По своему физическому смыслу величина S характеризует максимально возможный проигрыш в энерговыработке системы реакторов от пренебрежения оптимизацией и дает возможность судить о целесообразности оптимизации данной системы.
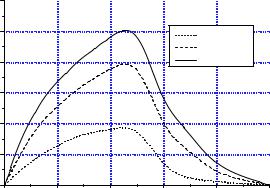
Результаты расчетов для конкретного случая, когда доли мощности реакторов одинаковы, приведены на рис. 2.11.
Как видно из рисунка, оптимизация дает тем больший эффект, чем больше параметр системы F отличается от единицы. Оптимизация системы наиболее существенна в области снижения мощности АЭС со 100 до 20 % номинальной.
Полученные результаты для реакторов с нелинейной зависимостью сводятся к следующим выводам.
Характер оптимальных распределений запасов реактивности и оптимальных степеней снижения мощности определяется величиной параметра системы
F = |
δ1a1 |
|
δ2 a2 |
. |
|
ϕ |
|
||||
|
|
ϕ |
2 |
|
|
|
1 |
|
|
|
|
143
S% |
60 |
|
|
|
|
|
|
оптимизации |
50 |
|
|
|
F=1 |
|
|
|
|
|
|
|
|||
|
|
|
|
F=2,F=0.5 |
|
||
40 |
|
|
|
F=3) |
|
||
|
|
|
|
|
|
||
эффект |
30 |
|
|
|
|
|
|
20 |
|
|
|
|
|
||
Максимальный |
|
|
|
|
|
||
10 |
|
|
|
|
|
||
0 |
|
|
|
|
|
||
0,0 |
0,2 |
0,4 |
0,6 |
0,8 |
1,0 |
||
|
|||||||
|
|
Степень снижения мощности системы,α |
|
||||
Рис. 2.11. Зависимость величины максимально возможного эффекта оптимизации от степени снижения мощности системы реакторов с нелинейной зависимостью ε(ρ) при различных величинах параметра F
Оптимальный режим эксплуатации реакторов может быть двух типов при F ≠ 1 и одного типа при F = 1.
Больший относительный запас реактивности следует создавать в реакторе с большей величиной комплекса δϕa . Этот реактор в пер-
вую очередь вовлекается в переменный режим работы.
Эффект оптимизации наиболее существен в диапазоне снижения мощности АЭС от 100 до 30 % и тем больше, чем больше параметр системы F отличается от единицы. Но даже в случае одинаковых реакторов ( F =1 ) эффект может быть существенным.
Например, из решения оптимизационной задачи для двух реакторов типа РБМК, следует что оптимальным является равномерное снижение мощности, а «антиоптимальным» – отработка переменного графика одним блоком.
При 50 % уровне снижения мощности АЭС максимально возможный эффект за компанию топлива составляет около ≈ 3 % от
энерговыработки системы, что соответствует ≈105 МВт сут
144
В целом, решение задачи по оптимизации распределения запасов реактивности в системе реакторов позволяет сделать следующие выводы.
1. Характер оптимального распределения запаса реактивности определяется величиной параметра системы F (для системы двух
реакторов F = δ1a1 δ2a2 ) и зависит от степени снижения мощно-
ϕ1 ϕ2
сти системы. В переменный режим работы, как правило, в первую очередь вовлекается реактор с большей величиной комплекса δϕa ,
иначе говоря, с худшим использованием топлива.
2.Возможный проигрыш от пренебрежения оптимизацией наиболее существенен в предполагаемом регулировочном диапазоне работы АЭС. Величина эффекта оптимизации тем больше, чем больше параметр системы отличается от единицы.
3.Решение рассмотренной задачи является также решением обратной задачи – об оптимальном распределении запасов реактивности с целью увеличения маневренных свойств системы (т.е.
уменьшения α) при заданной суммарной потере энерговыработки.
2.3. Формирование банковского портфеля максимальной доходности
2.3.1. Основные характеристики ценных бумаг
Одним из важных прикладных аспектов методов математического программирования и, в частности, нелинейного программирования является оптимизация банковской деятельности. Особое внимание уделяется оптимизации работы с ценными бумагами. В этой связи возникает актуальная задача формирования состава ценных бумаг банковского портфеля, обеспечивающих максимальную доходность банковских операций при работе с этими ценными бумагами при сохранении заданной величины риска.
Таким образом, основными понятиями при решении данной задачи являются [58]:
– доходность банковского портфеля;
145

– риск банковских операций с ценными бумагами, входящими в портфель.
Не вдаваясь в подробности банковских операций, рассмотрим основные характеристики ценных бумаг.
Банковский портфель представляет собой набор активов (пассивов), являющихся титулами собственности или иных благ (акции, валюта, ваучеры, аккредитивы и т.д.).
Ожидаемая доходность банковского портфеля есть взвешенная средняя ожидаемой доходности каждого из активов, входящих в портфель, где весами служат доли инвестиций в каждый из активов от всей суммы, вложенной в портфель:
n |
|
RpT (x1...xn ) = ∑RiTWi ; i =1, n , |
(2.96) |
i=1
где RpT – доходность всего инвестиционного портфеля за период времени T; RiT – доходность единицы i-го актива; Wi – доля инвестиций в i-й актив, от общей суммы инвестирования в портфель,
n
причем ∑Wi =1, xi – количество единиц i-й ценной бумаги.
i=1
Доходность единицы i-го актива за временной промежуток T определяется следующим образом:
RiT = ln (Pi (t) Pi (t −T )) . |
(2.97) |
Как следует из формулы (2.96), доходность инвестиционного портфеля будет зависеть от двух параметров: доходности отдельного актива, входящего в портфель и доли инвестиции в каждый актив.
Объем инвестиций, вложенных в портфель, будет равен сумме произведений стоимости единицы актива на его количество в портфеле:
n
V = ∑Vi xi .
i=1
Объем инвестиций, вложенных в отдельный актив портфеля, будет равен произведению стоимости единицы актива на количество единиц актива в портфеле:
V (xi ) =Vi xi , |
(2.98) |
146
где V(xi) – объем инвестиций, вложенных в i-ю ценную бумагу; Vi – цена единицы i-й ценной бумаги.
Долю инвестиций в каждый актив можно выразить следующим образом:
W = |
V (xi ) |
= |
Vi xi |
. |
(2.99) |
|
|
||||
i |
Vport |
|
Vport |
|
|
|
|
|
|||
Теперь формулу доходности портфеля (2.96) можно переписать в следующем виде:
n |
Vi xi |
|
|
|
RpT (x1...xn ) = ∑RiT |
. |
(2.100) |
||
|
||||
i=1 |
Vport |
|
||
Как уже отмечалось выше, важной характеристикой банковского портфеля является величина риска. Риск потери капитала в связи с неблагоприятной ситуацией, складывающейся на рынке, – один из наиболее актуальных в настоящее время параметров, характеризующих финансовый инструмент.
Одним из важнейших видов рисков является рыночный риск. Рыночный риск представляет собой возможность отрицательного изменения стоимости активов в результате колебания процентных ставок, курсов валют, цен акций, облигаций и товарных контрактов.
В современной теории риск-менеджмента наиболее распространена модель риска под названием value at risk или рисковая стои-
мость – VaR [58].
Концепция VaR призвана дать четкий и однозначный ответ на вопрос, возникающий при проведении операций на финансовых рынках: какой максимальный убыток мы рискуем понести за определенный период времени с заданной вероятностью для данного портфеля?
Из этого следует, что величина VaR для портфеля заданной структуры определяется как наибольший ожидаемый убыток и рассчитывается на определенный период времени в будущем (временной горизонт) с заданной вероятностью непревышения некоторого значения VaR (доверительный интервал) при данном предположении о характере поведения рынка (метод расчета).
Доверительный интервал и временной горизонт являются ключевыми параметрами при расчете величины VaR.
147
Так, значение рисковой стоимости VaR в 10 млн. долл. для временного горизонта в один день и доверительного интервала в 99 % будет означать, что вероятность потери в течение следующих 24 ч меньше 10 млн. долл. составит 99 %; а вероятность убытков, превышающих 10 млн. долл. в течение ближайших суток, равна 1 %;
Причем убытки, превышающие 10 миллионов долларов, ожидаются в среднем один раз в 100 дней торгов.
Таким образом, рисковая стоимость является денежным показателем, отражающим ожидаемые потери с заданной степенью достоверности. Очевидно, рисковая стоимость для i -го актива является разностью между текущим значением цены актива Vi (t) и её
прогнозным значением |
Vi,(1−α) (t + τ) , полученным для |
момента |
(t + τ) с доверительной |
вероятностью (1−α) . Таким |
образом, |
можно записать: |
|
|
VaRi,1−α (t + τ) = V (t) −Vi,(1−α) (t + τ) . |
(2.101) |
|
В настоящее время наибольшее распространение получил ковариационный метод (variance-covariance) расчета величины VaR [19]. В его основе лежит допущение о нормальном законе распределения изменений цен активов, входящих в портфель.
При нормально распределенной случайной величине доверительный интервал (1 – α) всегда характеризуется квантилью (k1−α ) ,
которая показывает положение искомого значения случайной величины относительно среднего, выраженного в количестве среднеквадратичных отклонений этой случайной величины σi от средне-
го значения [19].
Для наиболее часто используемых значений доверительного интервала в 95 и 99 % соответствующие квантили будут равны 1,65 и 2,33 стандартных отклонений.
В случае принятия гипотезы о нормальном законе распределения стоимости i -го актива прогнозируемое значение цены для однодневного временного среза (τ =1) и доверительной вероятности
(1−α) определяется по формуле |
|
Vi,(1−α) (t +1) = V (t) exp(−k1−ασi (t)) . |
(2.102) |
148
Последняя формула записана в предположении, что математическое ожидание однодневных доходностей равно нулю.
Стандартное отклонение σi (t) может быть оценено по ограни-
ченной выборке цен (историческому периоду наблюдений) i -го актива.
Интересующая нас величина VaRi для временного среза в один день и доверительной вероятности (1−α) может быть определена
следующим образом: |
|
VaRi,1−α (t +1) = Vi (t){[exp(−k1−ασi (t))] −1}. |
(2.103) |
При малых значениях величины − k1−ασi (t) |
выражение |
{[exp(−k1−ασi (t))] −1} можно заменить на выражение |
− k1−ασi (t) . |
Эта линейная аппроксимация для малых значений σi(t) основана на разложении исходной функции в ряд Тейлора. Весьма часто знак «–» опускают и оперируют абсолютным значением величины VaR.
В результате для i -го актива, состоящего из нескольких инструментов, величина рисковой стоимости с временным горизонтом в один день и доверительным интервалом (1 – α) может быть рассчитана по формуле:
VaRi = VaRi,1−α (t +1) = Vi (t)k1−ασi (t) ,
где Vi (t) – текущая стоимость позиции i -го актива (произведение
текущей цены на количество единиц актива).
Для рисковой стоимости с временным горизонтом Т дней и доверительным интервалом (1 – α) последняя формула принимает вид
VaRi =VaRi,1−α (t +1) =Vi (t)k1−ασi (t) T , |
(2.104) |
Соответствующая формула для расчета VaR всего банковского портфеля имеет вид
VaR = |
|
тΩ |
|
, |
(2.105) |
IVaR |
IVaR |
где IVaR – вектор столбец индивидуальных рисков позиций; Ω – корреляционная матрица доходностей факторов риска. В развернутом виде формула (2.105) принимает вид
149
n |
n n |
|
VaR = ∑VaRi2 |
+ 2∑ ∑ρijVaRiVaR j , |
(2.106) |
i=1 |
i=1 j=i+1 |
|
где VaRi – рассчитывается по формуле (2.104), а ρij – коэффици-
енты корреляции доходности финансового инструмента, которые рассчитываются следующим образом:
|
|
N N |
|
|
|
|
|
|
|
(σдох )i = |
∑∑Rik2 ; |
i = |
1, n |
, |
|
(2.107) |
|||
|
|
k =1l=1 |
|
|
|
|
|
|
|
|
N N |
|
|
|
|
|
|
|
|
|
∑∑Rik R jl |
|
|
|
|
|
|
||
ρij = |
k =1l=1 |
|
; |
i, j = |
|
. |
(2.108) |
||
|
1, n |
||||||||
|
|
||||||||
|
(σдох )i (σдох ) j |
|
|
|
|
|
|
||
В последней формуле Rik , R jl – реализовавшиеся доходности i- ого и j-го финансовых инструментов в моменты наблюдения k и l,
N– число наблюдений.
2.3.2.Постановка задачи формирования портфеля максимальной доходности при фиксированной
величине риска
Один из методов управления рисками – это наложение ограничений (лимитов) на величину риска VaR. При этом участники фондового рынка задаются определенной величиной VaR и стараются так сформировать свой портфель, чтобы его доходность была максимальной.
Учитывая формулу расчета доходности (2.100), запишем критерий, который необходимо максимизировать:
n |
n |
Vi xi |
|
|
J (x1...xn ) = R p (x1...xn ) = ∑ RiWi |
=∑ Ri |
. (2.109) |
||
|
||||
i=1 |
i=1 |
V port |
||
Инвестор, обладая ограниченными средствами, в состоянии инвестировать в рынок объем денежных средств, не превышающий Vport . В результате получаем ограничение:
150
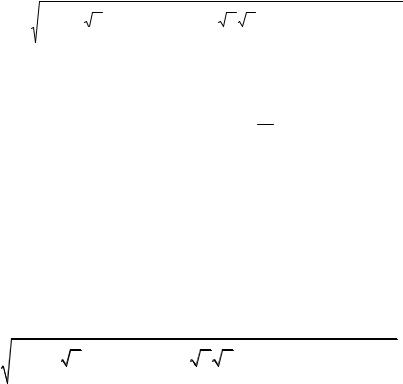
n |
|
∑Vi xi ≤ Vport . |
(2.110) |
i=1
Второе ограничение появляется из лимита на величину риска, при превышении которой позиция принудительно закрывается:
VaR ≤ VaRzad . |
(2.111) |
Подставив в (2.111) соотношения (2.106), (2.104), (2.98), полу-
чим рисковую стоимость для временного горизонта T:
n |
TVi xi σt )2 |
n n |
|
VaR = ∑(k1−α |
+ 2∑∑ρij T |
T (k1−αVi xi σt )(k1−αV j x j σt ) ≤ |
|
i=1 |
|
i=1 j=i |
|
|
|
≤ VaRzad . |
(2.112) |
Количество отдельных видов каждого актива не может быть отрицательным и является всегда целым, поэтому верно неравенство
xi ≥ 0 , xi Z; i =1,n .
Таким образом, задача формирования инвестиционного портфеля максимальной доходности, с заданными объемом инвестиций и значением риска выглядит следующим образом.
Найти
|
|
|
|
|
|
n |
V x |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
i |
|
||
|
|
max |
J (x1...xn ) |
= Rp (x1...xn ) = ∑Ri |
i |
|
|||
|
|
|
|||||||
|
|
|
|
|
|
i=1 |
|
|
|
|
|
|
|
|
|
Vport |
|||
при ограничениях |
|
|
|
|
|
|
|||
n |
|
|
|
|
|
|
|
|
|
∑Vi xi ≤Vport ; |
|
|
|
|
|
|
|||
i=1 |
|
|
|
|
|
|
|||
|
n |
n |
n |
|
|
|
|||
|
∑(k1−α TVi xiσi )2 + 2∑∑ T T ρij (k1−αVi xiσi )(k1−αVj xj σj ) ≤ |
||||||||
|
i=1 |
i=1 |
j=i |
|
|
|
|||
≤VaRzad ; |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
≥ 0, i =1, n; |
xi Z, i =1,n. |
|
|
|
|||||
xi |
|
|
|
||||||
Введем обозначения:
151
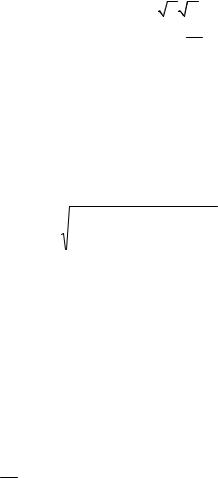
c |
= R |
Vi |
; |
d |
|
= ρ |
|
T T k2 VV |
σ |
σ |
; |
|
|
|
|||||||||
i |
i Vport |
|
|
ij |
|
ij |
1−α i j |
j |
i |
(2.113) |
|
ρii =1; i, j =1, n.
С учетом введенных обозначений, данную задачу можно записать в виде: найти
|
|
|
|
|
|
n |
|
|
||
|
|
|
|
|
|
|
(2.114) |
|||
|
|
|
max J (x1...xn ) = ∑ci xi |
|||||||
|
|
|
|
|
|
i=1 |
|
|
||
|
|
|
|
|
|
|
||||
при ограничениях |
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
∑Vi xi ≤Vport ; |
|
|
||||||||
i=1 |
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
n n |
|
|
|
∑dii xi2 + |
2∑∑dij xi x j |
≤VaRzad ; |
(2.115) |
||||||
|
i=1 |
|
|
|
|
i=1 j=i |
|
|
||
x |
|
≥ |
0, i = |
|
|
|
|
|
|
|
i |
1, n; |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xi Z, i =1, n. |
|
|
||||||||
2.3.3.Решение задачи формирования оптимального портфеля
сиспользованием множителей Лагранжа
Задача формирования банковского портфеля максимальной доходности с заданной величиной риска VaR, является задачей с линейным критерием и смешанными ограничениями, среди которых присутствуют как линейные, так и нелинейное ограничение. Так как максимизируемый критерий (2.114) и ограничения (2.115) (если пренебречь условием целочисленности аргументов оптимизации
xi , i =1, n ) являются выпуклыми дифференцируемыми функциями,
то поставленная задача может быть решена с помощью функций Лагранжа [1]. Учитывая, что данный метод предполагает минимизацию функции, запишем критерий задачи формирования инвестиционного портфеля в виде
n |
|
J (x1...xn ) = −∑ci xi , |
(2.116) |
i=1
152
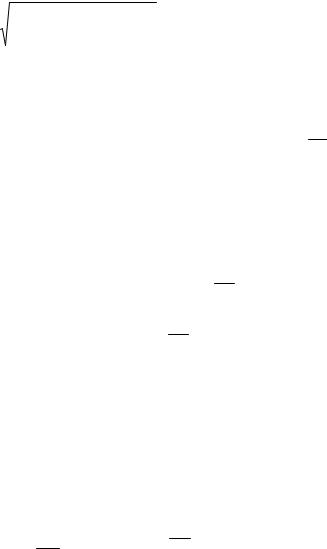
при этом ограничения примут следующий вид:
n |
|
|
|
|
|
∑Vi xi −V port ≤ 0; |
|
|
|||
i=1 |
|
|
|
|
|
|
n |
|
n n |
|
|
|
|
|
|
||
|
∑dii xi2 |
+ 2∑∑dij xi x j |
−VaRzad ≤ 0; |
(2.117) |
|
|
i=1 |
|
i=1 j=i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xi ≥ 0, i =1, n. |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
Поскольку метод множителей Лагранжа не был рассмотрен в гл. 3, остановимся на этом методе более подробно.
Обозначим левые части неравенств (2.117) через g j (x), j =1, m ,
а критерий минимизации (2.116) через функцию |
f (x) , тогда задача |
||
будет иметь следующий вид: найти |
|
||
min f (x) |
(2.118) |
||
при ограничениях |
|
||
g j (x) ≤ 0, j = |
|
. |
(2.119) |
1, m |
|||
Введем дополнительные переменные z j , j =1, m , и перейдем от ограничений неравенств (2.119) к ограничениям равенствам:
g j (x) + z 2j = 0, j =1, m .
Запишем функцию Лагранжа задачи (2.118), (2.120):
~ |
|
m |
2 |
] . |
|
|
|||
L(x, λ, z) = f (x) + ∑λ j [g j (x) + z j |
||||
j=1
Система уравнений для ее стационарных точек имеет вид
~ |
|
|
m |
∂g j |
|
|
|
|
∂L |
|
∂f |
|
|
|
|||
|
|
|
|
|||||
|
= |
|
+ ∑λ j |
|
= 0, i =1, n ; |
|||
∂xi |
∂xi |
∂xi |
||||||
|
j=1 |
|
|
|
||||
∂~
L = 2λ j z j = 0, j =1,.m ;
∂z j
(2.120)
(2.121)
(2.122)
(2.123)
153

~ |
|
|
|
|
|
∂L |
= g j (x) + z 2j = 0, |
|
. |
(2.124) |
|
j =1, m |
|||||
|
|||||
∂λ j |
|
||||
Условия (2.122) – (2.124) являются необходимыми условиями минимума задачи (2.118), (2.119). Очевидно, что равенства с вели-
чинами z 2j ≥ 0 эквивалентны неравенствам (2.119).
Исключим из этой системы вспомогательные переменные zj. Умножив каждое равенство из (2.123) на zj/2, получим: λ j z 2j = 0 или, как нетрудно убедиться из соотношения (2.124),
λ j g j = 0 . |
(2.125) |
С учетом последних соотношений необходимые условия минимума для задачи (2.118) – (2.119) принимают вид
∂L(x, |
|
) |
|
∂f (x) |
m |
∂g j (x) |
|
|
|
|
|
|
|
||||
λ |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
||||||||||
|
|
|
= |
|
|
|
+ ∑λ j |
|
|
= 0, |
i =1, n ; |
(2.126) |
|||||
∂xi |
∂xi |
∂xi |
|||||||||||||||
|
j=1 |
|
|
|
|
|
|
|
|||||||||
|
|
∂L(x, |
|
) = g j (x) ≤ 0, j = |
|
; |
|
||||||||||
|
|
λ |
(2.127) |
||||||||||||||
|
|
1, m |
|||||||||||||||
|
|
|
∂λ j |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
λ j g j (x) = 0, |
j = |
|
. |
|
|
|
(2.128) |
||||||
|
|
|
|
1,.m |
|
|
|
||||||||||
Существует следующая теорема [14].
Теорема. Пусть x* , λ* – решение системы (2.126) – (2.128). Тогда, если точка x* является решением задачи (2.126) – (2.128), то
λ*i ≥ 0 для всех i = 1, …, n.
С учетом вышеприведенной теоремы и выражений (2.126) – (2.128) можно сформулировать необходимые условия минимума в задаче (2.118) – (2.119) с допустимым множеством, удовлетворяю-
щим условию регулярности: если |
x* является решением задачи |
|||
(2.118) – (2.119), то для чисел λ*j , |
j =1, ..., n |
выполняются соотно- |
||
шения |
|
|
|
|
λ* j ≥ 0, j = |
|
; |
(2.129) |
|
1, m |
||||
154
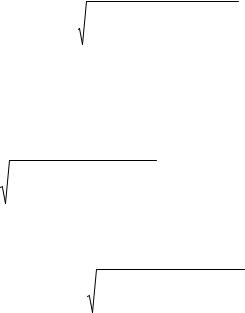
∂L(x* ) |
|
∂f (x) |
m |
λ* j |
∂g j (x* ) |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
||||||||
|
= |
|
+ ∑ |
|
|
|
|
= 0, |
i =1, n ; |
(2.130) |
|||||
∂xi |
∂xi |
|
∂xi |
||||||||||||
|
j=1 |
|
|
|
|
|
|
|
|
|
|||||
|
|
λ* j g j (x* ) = 0, |
j = |
|
|
; |
|
|
|
(2.131) |
|||||
|
|
1, m |
|
|
|
||||||||||
|
|
g j (x* ) ≤ 0, |
j = |
|
, |
|
|
|
(2.132) |
||||||
|
|
1, m |
|
|
|
||||||||||
которые называются условиями Куна – Такера [14].
Эти условия являются также и достаточными условиями мини-
мума в задаче (2.118) – (2.119).
Запишем функцию Лагранжа непосредственно для нашей задачи:
|
|
|
|
|
|
|
|
|
|
n |
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
L(x, λ) = −∑ci xi + λ1 ∑Vi xi |
−Vport |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
i=1 |
i=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
n n |
|
|
−VaRzad |
|
|
||
|
|
|
|
+ λ2 |
|
|
∑dii xi2 + 2∑ ∑dij xi x j |
|
. |
(2.133) |
||||||||
|
|
|
|
|
|
|
|
|
i=1 |
i=1 j=i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Запишем условия Куна – Такера: |
|
|
|
|
|
|
|
||||||||||
gi (x) ≤ 0, |
λi ≥ 0, |
i =1,2; |
|
|
|
|
|
|
|
|
||||||||
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
= 0; |
|
|
|
|
|
|
|
|
|
λ1 ∑Vi xi −V port |
|
|
|
|
|
|
|
|
||||||||||
|
|
i=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
n |
|
|
|
|
n |
n |
|
|
|
|
|
|
|
|
|
λ2 |
|
∑dii xi2 + 2∑∑dij xi x j |
−VaRzad |
= |
0; |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2.134) |
|
|
|
i=1 |
|
|
|
|
i=1 j=i |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
2dkk xk |
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ ∑dki xi |
|
|
|
|
|
|
|
||
|
|
|
|
|
1 |
|
|
|
|
i=1 |
|
|
|
|
|
|
|
|
c |
|
+ λ V |
+ |
λ |
|
|
|
|
i≠k |
|
|
|
|
= 0; k =1,..., n. |
|
|||
k |
|
2 |
|
n |
n n |
|
|
|
|
|
||||||||
|
|
1 k |
2 |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
∑dii xi2 + |
2∑∑dij xi x j |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
i=1 |
i=1 j=i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
155

Получили систему нелинейных уравнений. В отличие от систем линейных уравнений не существует решения нелинейных систем общего вида для прямых методов. Лишь в отдельных случаях системы подобного вида удается разрешить непосредственно в явном виде.
Для решения систем нелинейных уравнений обычно используют итерационные методы. Наиболее простым с точки зрения программной реализации и, кроме того, обладающим оптимальной скоростью сходимости является метод решения систем нелинейных уравнений Ньютона.
В основе метода Ньютона [2] лежит разложения функций в ряд Тейлора, причем члены, содержащие вторые (и более высоких порядков) производные, отбрасываются.
Пусть приближенные значения неизвестных системы (2.134) (например, полученные на предыдущей итерации) равны соответственно a1 , ..., an , b1 , b2 . Задача состоит в нахождении приращений
(поправок) к этим значениям |
|
x1, ..., xn , |
|
λ1, |
λ2 , |
благодаря ко- |
||||||||||||
торым решение системы (2.134) запишется в виде |
|
|
|
|||||||||||||||
x |
= a + |
x ,..., x |
n |
= a |
n |
+ x |
n |
,λ |
1 |
= b + |
λ |
1 |
, λ |
2 |
= b |
+ λ |
2 |
.(2.135) |
1 |
1 |
1 |
|
|
|
1 |
|
|
2 |
|
|
|||||||
Полученная в результате система линейных уравнений решается методом Гаусса относительно поправок x1 , ..., xn , λ1 , λ2 .
Алгоритм решения задачи формирования оптимального портфеля максимальной доходности, с заданной величиной риска VaR может быть представлен следующей последовательностью действий.
1.Задаем начальные приближения ai, b (i =1, …, n; j = 1, 2) для системы линейных уравнений (2.134).
2.Задаем ε – точность, с которой необходимо получить решение задачи.
3.Решаем систему линейных уравнений (2.134) методом Гаусса
относительно приращений xi (i =1, n) и λ j ( j =1, 2) .
4. После нахождения решения задаем начальные приближения равными следующим величинам: ati = at−1,i + xi , bt, j = bt−1,i + λ j , здесь t – номер итерации.
156

5. Проверяем выполнение неравенства xi ≤ ε и λ j ≤ ε , если
эти условия выполняются, то переходим к шагу 6. Если нет, то переходи к шагу 1, где начальные приближения задаем равными величинам, полученным в пункте 4.
6. Принимаем xi* = ai , i =1, n , и выходим из цикла решения задачи.
2.3.4.Пример задачи формирования оптимального портфеля
Вкачестве тестового примера была взята ситуация из реальной жизни одного из участников фондового рынка России в 2003–2004 гг.
Объем денежных средств, которые трейдер в состоянии инвестировать в рынок ценных бумаг, равен 60 000 000 руб. Временной горизонт, на который делается расчет инвестиционного портфеля, равен одной неделе или семи дням. Доверительный интервал равен 95 %. Величина допустимого риска (VaR) равна 1 800 000 руб. То есть вероятность того, что наши убытки не превысят 1 800 000 руб.
втечение недели, равна 5 %.
С использованием истории цен на акции с начала 2002 г. по конец первого квартала 2004 г. были рассчитаны доходность (см. формулу (2.97)) и индивидуальный риск (см. формулу (2.104)) акций каждого эмитента.
При составлении выражения для риска диверсифицированного портфеля была рассчитана ковариационная матрица доходностей акций (см. формулы (2.107), (2.108)), на диагонали которой стоят дисперсии доходностей бумаг.
Ниже представлены результаты расчета банковского портфеля по приведенной выше методике за различные промежутки времени. В табл. 2.2–2.6 указаны доля акций каждого эмитента в портфеле
Wi |
= |
|
Vi xi |
, доли доходности, которые вносит каждая из бумаг в |
|
|
|||
|
|
V port |
||
портфель и общая доходность портфеля, вычисленная по формуле
(2.100).
157
Таблица 2.2
Оптимальный портфель максимальной доходности, рассчитанный по историческим данным в период с 1 по 31 марта 2003 г., %
Акция |
GSPBEX |
LKO |
YUKO |
SNGS |
SNGSP |
SIBN |
TATN |
TATNP |
EESP |
EESR |
MSNG |
IRGZ |
RTK |
RTKMP |
AVAZ |
GMK |
SBER |
AFLT |
||
H |
P |
M |
N |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Доля |
акций |
0.00 |
7.76 |
0.96 |
8.26 |
10.22 |
2.35 |
5.07 |
3.68 |
3.44 |
5.41 |
5.04 |
9.71 |
6.11 |
7.19 |
2.07 |
9.89 |
2.41 |
10.44 |
|
данного эмитента |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
в портфеле |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Доля доходности, |
0.00 |
0.28 |
0.13 |
-0.04 |
0.21 |
0.52 |
0.63 |
0.23 |
-0.01 |
0.11 |
0.09 |
0.34 |
0.35 |
0.96 |
0.04 |
0.93 |
0.68 |
0.01 |
||
которую |
акция |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
вносит в |
доход- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ность портфеля |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Доходность |
5.44 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
портфеля |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
158
Таблица 2.3
Оптимальный портфель максимальной доходности, рассчитанный по историческим данным в период с 1 по 30 июня 2003 г., %
Акция |
GSPBEX |
LKO |
YUKO |
SNGS |
SNGSP |
SIBN |
TATN |
TATNP |
EESP |
EESR |
MSNG |
IRGZ |
RTK |
RTKMP |
AVAZ |
GMK |
SBER |
AFLT |
||
H |
P |
M |
N |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Доля |
акций |
12.90 |
6.28 |
1.23 |
5.98 |
8.18 |
5.82 |
4.98 |
3.85 |
0.00 |
2.25 |
0.88 |
7.89 |
5.69 |
6.82 |
3.73 |
9.56 |
4.99 |
8.97 |
|
данного эмитента |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
в портфеле |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Доля доходности, |
0.18 |
0.05 |
0.07 |
0.06 |
0.19 |
0.46 |
0.37 |
0.01 |
0.00 |
0.31 |
0.16 |
0.37 |
0.29 |
0.83 |
-0.35 |
0.56 |
0.56 |
0.10 |
||
которую |
акция |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
вносит в |
доход- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ность портфеля |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Доходность |
4.22 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
портфеля |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 2.4
Оптимальный портфель максимальной доходности, рассчитанный по историческим данным в период с 1 по 30 сентября 2003 г., %
Акция |
GSPBEX |
LKO |
YUKO |
SNGS |
SNGSP |
SIBN |
TATN |
TATNP |
EESP |
EESR |
MSNG |
IRGZ |
RTK |
RTKMP |
AVAZ |
GMK |
SBER |
AFLT |
||
H |
P |
M |
N |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Доля |
акций |
0.00 |
3.83 |
0.51 |
2.44 |
6.51 |
3.38 |
6.73 |
5.57 |
3.18 |
8.28 |
3.86 |
9.44 |
5.51 |
8.25 |
5.23 |
12.28 |
4.23 |
10.78 |
|
данного эмитента |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
в портфеле |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Доля доходности, |
0.00 |
0.17 |
0.05 |
0.10 |
0.22 |
0.23 |
0.70 |
0.26 |
1.19 |
3.19 |
1.02 |
1.02 |
0.61 |
1.33 |
-0.18 |
2.38 |
0.57 |
1.00 |
||
которую |
акция |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
вносит в |
доход- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ность портфеля |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Доходность |
13.86 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
портфеля |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
159
Таблица 2.5
Оптимальный портфель максимальной доходности, рассчитанный по историческим данным в период с 1 по 31 декабря 2003 г., %
Акция |
GSPBEX |
LKO |
YUKO |
SNGS |
SNGSP |
SIBN |
TATN |
TATNP |
EESP |
EESR |
MSNG |
IRGZ |
RTK |
RTKMP |
AVAZ |
GMK |
SBER |
AFLT |
||
H |
P |
M |
N |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Доля |
акций |
17.51 |
4.65 |
0.00 |
5.86 |
5.95 |
2.34 |
3.62 |
3.99 |
3.94 |
5.35 |
4.26 |
5.87 |
6.10 |
6.10 |
3.71 |
8.86 |
3.67 |
8.20 |
|
данного эмитента |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
в портфеле |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Доля доходности, |
2.33 |
0.35 |
0.00 |
0.76 |
0.66 |
0.16 |
0.29 |
0.23 |
1.14 |
1.64 |
0.99 |
0.74 |
0.81 |
0.99 |
0.01 |
2.79 |
0.30 |
1.38 |
||
которую |
акция |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
вносит в |
доход- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ность портфеля |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Доходность |
15.57 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
портфеля |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2.4. Определение начальных условий движения космического аппарата
2.4.1. Математическая модель движения космического аппарата
В настоящих расчетах будем использовать неинерциальную систему прямоугольных координат, связанную с вращающейся Землей: центр системы координат совпадает с центром Земли, основная плоскость OXY совпадает с плоскостью экватора, ось OX – направлена на точку пересечения плоскости орбиты спутника в восходящем узле с плоскостью экватора в начальный момент времени, ось OZ совпадает с осью вращения Земли, ось OY дополняет систему до правой. Далее эту систему будем называть мгновенной системой координат. Данная система координат такая же, как гринвичская, а отличается от нее лишь начальным углом поворота.
Выбор этой системы удобен по следующим причинам.
1.Правые части уравнений движения не являются громоздкими.
2.Не нужен контроль положения гринвичского меридиана.
3.Координаты наблюдательного пункта (НП) постоянны, что удобно для оценки параметров движения.
Будем использовать следующую упрощенную модель движения: космический аппарат (КА) движется в центральном поле сил земного притяжения; модель Земли – сфера. Фактически это задача невозмущенного движения КА. Задача при таких допущениях имеет аналитическое решение, что позволяет проверить численную методику расчета на тестовых орбитах.
Уравнения движения будут иметь вид
x |
Vx |
; |
|
|
|
|
|
|
|
|
|
|
y |
Vy |
; |
|
|
|
|
|
|
|
|
|
|
z |
V ; |
|
|
|
|
|
||||||
|
|
z |
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
||||
Vx |
|
|
r3 |
|
|
x 2 Vy |
; |
(2.136) |
||||
V |
|
y |
|
2 y 2 V |
; |
|
||||||
r3 |
|
|
||||||||||
|
y |
|
|
|
|
|
|
x |
|
|
||
|
|
|
|
z |
|
|
|
|
|
|
||
V |
|
|
, |
|
|
|
||||||
|
|
|
|
|||||||||
z |
|
|
|
|
r3 |
|
|
|
|
|
||
160

где Ω = 7,292115 |
10–5 с–1 – угловая скорость вращения Земли; |
μ = 398605 109 м3/с2 – произведение гравитационной постоянной |
|
на массу Земли; x, |
y, z – координаты КА; Vx, Vy, Vz – скорости КА; |
r 
 x2 y2 z2 – модуль радиус-вектора КА.
x2 y2 z2 – модуль радиус-вектора КА.
Первые слагаемые в правых частях уравнений для производных скоростей КА системы (80) являются проекциями силы тяготения на соответствующие оси. Второе и третье слагаемые в уравнениях для производных скоростей Vx и Vy обусловливают переход в неинерциальную вращающуюся систему координат.
Начальные условия определяются по данным траекторных измерений, которые образуют массив измеренных текущих навигационных параметров (ИТНП). При этом под траекторными измерениями понимаются измерения радиальной скорости D спутника относительно НП. Измерения радиальной скорости производятся с наземного НП в согласовании с бортом КА. Выбор радиальной скорости КА в качестве измеряемой функции обусловлен конструктивными возможностями системы.
Рассматривается движение КАна пассивном участке траектории. Во введенной ранее мгновенной системе координат состояние КА характеризуется в каждый момент времени t тремя координа-
тами x, y, z и тремя компонентами вектора скорости Vx, Vy, Vz.
Эти шесть параметров однозначно определяются через некоторые
НУ x0, y0, z0, Vx0, Vy0, Vz0 как решение задачи Коши. Таким образом, x0, y0, z0, Vx0, Vy0, Vz0 однозначно определяют траекторию движения КА по
теореме осуществовании и единственности решения задачи Коши. Введем обозначение Q = {x, y, z, Vx, Vy, Vz}. В момент времени tn
производят измерение функции D параметров траектории
|
|
|
Dn |
D (Q,tn ), |
|
|
(2.137) |
D (x xнп )2 (y yнп )2 (z zнп)2 , |
|
||||||
D |
1 |
(x xнп)Vx |
(y yнп)Vy |
(z zнп)Vz , |
(2.138) |
||
|
|||||||
|
D |
|
|
|
|
||
где D – радиальная дальность КА относительно НП; D – радиальная скорость; x, y, z, Vx, Vy, Vz – соответственно координаты и скорости КА в гринвичской системе координат, xнп, yнп, zнп – координаты НП. Как видно из (2.138); D – является функцией от текущих параметров траектории, которые зависят от НУ.
161
При этом измерения проводятся со среднеквадратичной ошибкой σn. Измеренное значение обозначим Dn изм .
Совокупность значений Dn изм (n = 1…N) функции D , измере-
ния которой проводятся в процессе полета КА на определенном промежутке времени, образует множество траекторных измерений.
Таким образом, задача обработки траекторных измерений и, соответственно, данного модуля формулируется следующим образом: определить неизвестные параметры x0, y0, z0, Vx0, Vy0, Vz0, характеризующие движение КА по информации о его траектории в виде измерений Dn изм , n = 1…N, полученных с известной точно-
стью и проведенных в моменты времени t1, t2, …, tN.
В качестве основной апостериорной информации о траектории методика определения параметров КА использует траекторные измерения. Предполагаем, что ошибки этих измерений носят случайный характер, некоррелированы между собой и распределены по нормальному закону с нулевым математическим ожиданием и известной дисперсией.
Наряду с рассмотренной апостериорной информацией для определения параметров движения используется и априорная информация о траектории, которая содержит ожидаемые значения определяемых параметров Q. Эти значения определяются в результате обработки предыдущих сеансов измерений и дальнейшего прогнозирования по ним параметров траектории КА.
Избыточность измерений (по сравнению с числом определяемых параметров) и случайный характер их ошибок вызывают необходимость статистического подхода к решению поставленной задачи. Результатом такого подхода и принятых допущений о характере ошибок измерений явился выбор в качестве статистического метода – метода наименьших квадратов.
Метод наименьших квадратов (МНК), применяемый для определения параметров Q0 траектории по измерениям
D1изм , D2изм , …, DN изм ,
приводит к необходимости минимизации целевой функции
N |
1 |
(Di Di изм )2 |
|
|
||
|
|
|
, |
(2.139) |
||
i |
2 |
|||||
i 1 |
|
|
|
|||
162
где Dn – расчетное значение радиальной скорости; σi – средне-
квадратическое отклонение измеренного значения.
Запишем для целевой функции (2.139) необходимые условия существования экстремума:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0; |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0; |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
y0 |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0; |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z0 |
|
|
|
|
|
|
|
|
|
(2.140) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0; |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Vx0 |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0; |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V |
y |
0 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
Vz0 |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
или же |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
D |
|
|
|
|
|
|||||
|
|
|
|
2 |
(Di Di изм ) |
|
0; |
||||||||||||||||||||||
x0 |
i2 |
x0 |
|||||||||||||||||||||||||||
|
|
|
i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
N |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
D 0; |
||||||||||
|
|
|
|
2 (Di Di изм ) |
|||||||||||||||||||||||||
y0 |
i2 |
||||||||||||||||||||||||||||
|
|
|
i 1 |
|
|
|
|
|
|
|
|
|
|
y0 |
|
|
|
|
|||||||||||
|
|
|
|
N |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
D |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
2 |
(Di Di изм ) |
|
|
|
|
0; |
|||||||||||||||
z0 |
|
|
2 |
z0 |
|||||||||||||||||||||||||
|
|
|
i 1 |
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
(2.141) |
|||||||||||
|
|
|
|
N |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
D |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
(Di Di изм ) |
|
|
|
|
|
0; |
|||||||||||
Vx0 |
|
2 |
Vx0 |
||||||||||||||||||||||||||
|
i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
D |
|
|
|
||||||||
|
|
|
|
|
|
2 (Di Di изм ) |
|
|
0; |
||||||||||||||||||||
Vy0 |
|
i2 |
|
Vy0 |
|
||||||||||||||||||||||||
|
|
i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
N |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
D |
|
|
|||||||||
|
|
|
|
|
|
2 |
(Di Di изм ) |
|
|
0, |
|||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
V |
|
|
|
|||||||||||||||||
V |
z0 |
|
i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
z0 |
|
|
|||||||||||
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
163

где
|
D |
|
|
|
D |
|
|
|
x |
|
|
D |
|
|
|
|
|
y |
|
D |
|
|
|
|
z |
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
x0 |
|
x |
|
|
|
x0 |
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x0 |
|
z |
|
|
|
|
x0 |
||||||||||||||||||||||||||||||||||
|
|
|
|
D |
|
V |
x |
|
D |
|
Vy |
|
|
|
|
D |
|
V |
z |
; |
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
V |
x |
|
x |
|
V |
y |
|
x |
|
|
|
V |
z |
x |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|||||||||||||||
|
D |
|
|
|
D |
|
|
|
|
|
x |
|
|
|
D |
|
|
|
|
|
y |
D |
|
|
|
|
z |
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
y0 |
|
|
x |
|
|
|
|
y0 |
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y0 |
|
z |
|
|
|
|
y0 |
||||||||||||||||||||||||||||||||||
|
|
|
|
D |
|
V |
x |
|
D |
|
Vy |
|
|
|
|
D |
|
V |
z |
; |
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
Vx |
|
|
|
|
|
|
|
|
Vy |
|
y0 |
|
|
|
Vz |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
y0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
y0 |
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
D |
|
|
|
D |
|
|
x |
|
|
D |
|
|
|
|
y |
D |
|
|
|
|
z |
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
z0 |
|
x |
|
|
z0 |
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z0 |
|
z |
|
|
|
|
z0 |
||||||||||||||||||||||||||||||||||
|
|
|
|
D |
|
V |
x |
|
D |
|
Vy |
|
|
|
|
D |
|
V |
z |
; |
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
Vx |
|
|
|
|
|
|
|
|
Vy |
|
z0 |
|
|
|
Vz |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
z0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
z0 |
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
D |
|
|
|
D |
|
|
|
x |
|
|
|
D |
|
|
|
|
|
y |
|
D |
|
|
|
|
z |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
Vx0 |
|
|
|
Vx0 |
|
y |
|
|
Vx0 |
|
|
Vx0 |
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
D |
|
V |
x |
|
|
|
|
D |
|
|
Vy |
|
|
|
|
D |
|
|
V |
z |
; |
|||||||||||||||||||||||||||||||||||
|
Vx |
|
|
|
|
|
|
|
|
|
Vy |
Vx0 |
|
|
|
Vz |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
Vx0 |
|
|
|
|
|
|
|
|
|
|
|
|
Vx0 |
|||||||||||||||||||||||||||||||||||||||
|
D |
|
|
|
|
D |
|
|
|
|
x |
|
|
|
D |
|
|
|
|
|
y |
|
D |
|
|
|
|
|
z |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
Vy0 |
|
|
|
|
x |
|
|
|
|
Vy0 |
|
|
y |
|
|
|
Vy0 |
|
|
z |
|
|
|
|
|
|
Vy0 |
|||||||||||||||||||||||||||||||
|
|
|
D |
|
|
V |
x |
|
|
|
|
|
D |
|
|
|
Vy |
|
|
|
|
D |
|
|
V |
z |
; |
|||||||||||||||||||||||||||||||
|
|
Vx |
|
|
|
|
|
|
|
|
|
|
|
|
Vy |
|
Vy0 |
|
|
|
Vz |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
Vy0 |
|
|
|
|
|
|
|
|
|
|
|
|
Vy0 |
|||||||||||||||||||||||||||||||||||||||
|
D |
|
|
|
D |
|
|
|
x |
|
|
|
D |
|
|
|
|
|
y |
|
D |
|
|
|
|
|
z |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
Vz0 |
|
|
|
Vz0 |
|
y |
|
|
Vz0 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
Vz0 |
|||||||||||||||||||||||||||||||||||
D Vx D Vy D Vz ,Vx Vz0 Vy Vz0 Vz Vz0
(2.142)
частные производные по текущим параметрам определяются в виде
164
D |
|
Lx |
Vx D2 x |
2 Vx |
; |
||||||||||
x |
|
|
|
D3 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|||||||
D |
|
Ly |
Vy D2 y |
2 Vy |
|
|
; |
||||||||
y |
|
|
|
D3 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|||||||
D Lz |
Vz D2 z2 Vz |
; |
|
||||||||||||
|
|
|
|
|
|
|
|||||||||
z |
|
|
|
|
D3 |
|
|
|
|
(2.143) |
|||||
D |
|
Mx |
x xнп |
; |
|
|
|
|
|
||||||
Vx |
|
|
|
|
|
|
|
||||||||
|
|
|
|
D |
|
|
|
|
|
|
|||||
D |
|
My |
y yнп |
|
; |
|
|
|
|
|
|||||
Vy |
|
D |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
||||||
D |
Mz |
z zнп |
, |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
||||||||
Vz |
|
|
|
|
D |
|
|
|
|
|
|
||||
где xнп, yнп, zнп – координаты НП.
2.4.2. Выбор алгоритма решения
Решение методом Ньютона – Гаусса сводится к серии последовательных приближений. Число приближений зависит от степени близости выбранного нулевого приближения x0(0) , y0(0) , z0(0) , Vx(00) ,
Vy(00) , Vz(00) к точному решению.
Пусть на (s – 1) приближении для параметров получены значения Q(s 1) , тогда разлагаем в ряд Тейлора в окрестностях этих зна-
чений параметров значение D |
на приближении s и отбрасываем |
|||||||||||||||||||||
члены порядка выше первого: |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
D |
(s) |
D |
(s 1) |
|
D |
(s) |
|
D |
|
(s) |
|
D |
|
(s) |
|
|||||||
|
|
|
x0 |
x0 |
y0 |
y0 |
z0 |
z0 |
||||||||||||||
|
|
|
D |
|
|
|
D |
|
|
D |
|
|
(2.144) |
|||||||||
|
|
|
V |
(s) |
|
V |
(s) |
|
V |
(s) |
, |
|||||||||||
|
|
|
||||||||||||||||||||
|
|
|
|
x0 |
|
y0 |
|
|
|
z0 |
|
|||||||||||
|
|
Vx0 |
Vy0 |
Vz0 |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
165
где
x0(s) x0(s) x0(s 1); |
|
|
|||
y(s) |
y(s) y |
(s 1); |
|
|
|
0 |
0 |
0 |
|
|
|
z0(s) z0(s) z0(s 1); |
|
(2.145) |
|||
Vxo(s) Vxo(s) Vxo(s 1) |
; |
||||
|
|||||
Vyo(s) Vyo(s) Vyo(s 1); |
|
||||
Vzo(s) Vzo(s) Vzo(s 1) , |
|
||||
частные производные вычисляются |
при |
x0 x0(s 1) , |
y0 y0(s 1) , |
||
z0 z0(s 1) , Vx0 Vx(0s 1) , Vy0 Vy(0s 1) , Vy0 Vy(0s 1) .
Подставляя выражение (2.144) в необходимые условия экстремума (2.141), приходим к нормальной системе линейных уравнений относительно поправок
q(s) { x(s), y(s), z(s), Vx(s), Vy(s), Vz(s)}.
Введем следующие обозначения: x0 = q1, y0 = q2, z0 = q3, Vx0 = q4, Vy0 = q5, Vz0 = q6. Тогда с учетом этих обозначений получим сле-
дующий вид системы
|
|
|
|
N |
1 |
|
|
m |
Di |
|
(s) |
|
Di |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
qj |
|
|
|
|
|||||
|
|
|
|
2 |
|
qj |
qk |
|
|||||||||||
|
|
|
|
i 1 |
i |
|
|
j 1 |
|
|
|
|
|
|
|||||
N |
1 |
|
|
Di(s 1) |
Di изм |
Di |
|
|
|
|
|
||||||||
|
|
|
, |
k = 1, …, 6, |
(2.146) |
||||||||||||||
i |
2 |
|
|||||||||||||||||
i 1 |
|
|
|
|
|
|
|
|
|
qk |
|
|
|
|
|||||
или |
|
|
|
|
1 Di |
Di q(js) |
|
||||||||||||
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
N |
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
qj |
qk |
|
|
|
|
||||||
|
|
|
|
|
i 1 j 1 |
i2 |
|
|
|
|
|
||||||||
N |
1 |
|
Di |
(s 1) |
Di изм Di , k = 1, …, 6; |
|
|||||||||||||
|
|
(2.147) |
|||||||||||||||||
|
i |
2 |
|
|
|
|
|||||||||||||
i 1 |
|
|
|
|
|
|
|
|
|
|
qk |
|
|
|
|
||||
Производные по уточняемым параметрам вычисляются при qi qi(s 1) , i = 1, …, 6:
166
m
Ajk q(js) Bk , k = 1, …, 6, (2.148)
j 1
где
|
|
|
N |
1 |
|
Di |
|
Di |
|
|
|
|
||
Ajk |
|
|
|
, |
|
(2.149) |
||||||||
i2 |
qj |
qk |
||||||||||||
|
|
i 1 |
|
|
|
|
|
|
||||||
N |
1 |
|
|
Di(s 1) Di изм |
|
Di |
|
|
||||||
Bk |
|
|
. |
(2.150) |
||||||||||
i |
2 |
|
|
|||||||||||
i 1 |
|
|
|
|
|
|
|
|
qk |
|
||||
Таким образом, на каждом приближении для определения поправок к параметрам, полученным на предыдущем приближении, решатся система уравнений (2.148) методом Гаусса.
Матрица и правые части этой системы формируются для каждого приближения при помощи выражений (2.149) из производных и рассогласований между наблюденными значениями измеряемой величины и ее расчетными значениями, причем производные и рассогласования считаются для траектории, определяемой параметрами предыдущего приближения, для каждого момента времени и каждой наблюдаемой величины.
Для вычисления производных
x |
, |
|
|
y |
, |
|
z |
|
, |
Vx |
, |
|
Vy |
|
, |
Vz |
, |
|
|
|
|
|
|
|
|
||||||||||||||||||
x0 |
|
|
x0 |
|
x0 |
x0 |
|
x0 |
|
|
x0 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
x |
|
, |
|
|
y |
|
, |
|
z |
|
|
, |
Vx |
, |
|
Vy |
|
, |
Vz |
, |
|
|
|
|
|
|
|
|
|||||||||||||||
y0 |
|
|
|
y0 |
|
|
y0 |
|
y0 |
|
y0 |
|
|
y0 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
x |
, |
|
|
y |
, |
|
z |
|
, |
Vx |
, |
Vy |
|
|
, |
|
Vz |
, |
|
|
|
|
|
|
|
|
|||||||||||||||||
z0 |
|
|
z0 |
|
z0 |
z0 |
|
z0 |
|
|
|
z0 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
x |
|
|
|
, |
|
y |
|
, |
|
|
|
|
z |
, |
|
Vx |
|
, |
|
|
|
Vy |
|
, |
|
|
|
Vz |
, |
||||||||||||||
Vx0 |
|
Vx0 |
|
Vx0 |
Vx0 |
|
|
|
Vx0 |
|
|
Vx0 |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
x |
|
|
|
|
, |
|
y |
|
|
, |
|
|
|
|
z |
|
, |
|
Vx |
|
|
, |
|
Vy |
|
|
|
, |
|
Vz |
|
, |
|||||||||||
Vy0 |
|
|
Vy0 |
|
|
|
Vy0 |
|
|
Vy0 |
|
|
|
Vy0 |
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Vy0 |
||||||||||||||||||||||||
x |
|
|
|
, |
|
y |
|
, |
|
|
|
|
z |
, |
|
Vx |
|
, |
|
|
|
Vy |
, |
|
|
|
Vz |
|
, |
||||||||||||||
Vz0 |
|
Vz0 |
|
Vz0 |
Vz0 |
|
Vz0 |
|
Vz0 |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
167
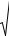
используется разностная схема |
x |
и т.д., где x0 – приращение по |
|
||
|
x0 |
|
координате x0, x – изменение координаты х при изменении x0 на
x0.
Для вычисления производных по такой схеме одновременно интегрируется семь систем уравнений движения со следующими начальными условиями (НУ):
1)x0, y0, z0, Vx0, Vy0, Vz0;
2)x0 + x0, y0, z0, Vx0, Vy0, Vz0;
3)x0, y0 + y0, z0, Vx0, Vy0, Vz0;
4)x0, y0, z0 + z0, Vx0, Vy0, Vz0;
5)x0, y0, z0, Vx0 + Vx0, Vy0, Vz0;
6)x0, y0, z0, Vx0, Vy0 + Vy0, Vz0;
7)x0, y0, z0, Vx0, Vy0, Vz0 + Vz0.
Для каждого приближения вычисляется величина среднеквадратичной ошибки веса
(s) |
|
|
|
, |
(2.151) |
|
|||||
0 |
|
N m |
|
||
|
|
|
|||
где N – общее количество измерений, участвующих в обработке на данном приближении; m – количество уточняемых параметров. Величина σ0 служит мерой разброса измерений вокруг траектории, определяемой параметрами, полученными в результате предыдущего приближения.
Ввиду возможноcти сильных флуктуаций в информации об измерениях отбор информации производится с использованием траектории, полученной в предыдущем приближении. В результате такого отбора в формировании коэффициентов Ajk и правых частей (2.148) Bk принимают участие лишь те траекторные измерения, для которых выполняется неравенство
1 |
|
|
Di Di изм |
|
o(s) , |
(2.152) |
|
|
|
||||||
|
|||||||
i |
|
|
|
|
|
||
где ν – параметр отбора, который при обработке информации, содержащей измерения со случайными ошибками, рекомендуется положить равным 3.
168
Эти вычисления завершаются приближением с номером s, для которого впервые выполняется неравенство
|
qi |
|
i , i = 1, …, 6, |
(2.153) |
|
|
где εi – набор заданных погрешностей. Сходящийся процесс приближений сопровождается уменьшением среднеквадратичной
ошибки σ0.
Для проверки работоспособности данного алгоритма была построена имитационная модель. Была взята круговая орбита с наклонением 82,5 град., периодом обращения по ней Т = 7200 с, ра-
диусом r = 8059028,026032 м, v = 7032.828678 м/с. Для этой орбиты брались начальные условия в неподвижной системе координат:
x0 = 8059028.026032, y0 = 0.0, z0 = 0.0, |
|
Vx0 = 0.0, Vy0 = 917.968348, Vz0 = 6972.661854. |
(2.154) |
Эти условия переводились в подвижную систему координат, ось OX которой в начальный момент времени совпадает с осью OX неподвижной системы координат.
Формулы пересчета выглядят следующим образом:
x0 подв |
x0 неподв , |
|
|
|
y0 неподв , |
|
|
y0 подв |
|
|
|
|
z0 неподв , |
|
|
z0 подв |
|
(2.155) |
|
|
Vx0 неподв |
|
|
Vx0 подв |
y, |
|
|
|
Vy0 неподв |
x, |
|
Vy0 подв |
|
||
|
Vz0 неподв . |
|
|
Vz0 подв |
|
|
Начальные условия в подвижной системе координат будут иметь вид: x0 = 8059028.026032, y0 = 0.0, z0 = 0.0, Vx0 = 0.0, Vy0 = 330.294756, Vz0 = 6972.661854.
Были взяты следующие координаты НП: xнп = 4510634.1572, yнп = 4510634.1572, zнп = 0.0.
Далее интегрировалась система уравнений движения (2.136) с указанными начальными условиями методом Рунге – Кутта с шагом интегрирования h = 1 c на отрезке времени 48 ч. Полученная траектория принималась за истинную.
169
Из полученного массива координат выбирались только те витки, угол места для измерений на которых близок к 90 град. и НП оказывался практически в плоскости витка. По получившимся данным массива координат и скоростей рассчитывалась радиальная скорость D (89), которая затем зашумлялась генератором случайных чисел с заданным СКО. Этот массив значений радиальной скорости КА считался входным массивом измеренных значений.
Варьируя НУ и СКО шума, оценивалась работа алгоритма. В результате работы выяснилось, что алгоритм расходится и не дает близкого к НУ результата. Это происходит потому, что получаемая
впроцессе работы алгоритма нормальная система линейных уравнений имеет плохо обусловленную основную матрицу. В результате численный поиск решения затрудняется, а ошибки вычислений становятся слишком большими.
Метод минимизации Ньютона – Гаусса не дал приемлемых результатов из-за плохой обусловленности матрицы нормальной системы линейных уравнений относительно невязок уточняемых параметров. Поэтому для минимизации функционала использовался метод покоординатного спуска с минимизацией по каждой из координат методом деления шага пополам. Этот метод лишен недостатка метода Ньютона – Гаусса. Он прост в реализации и хорошо зарекомендовал себя в различных задачах оптимизации. Основной недостаток этого метода – высокая вычислительная сложность, что,
всвою очередь, ведет к росту времени работы алгоритма.
При различных НУ и величинах СКО шума метод обладает малой скоростью сходимости и удовлетворительный результат не был получен во всех случаях из-за больших временных затрат. Причем на начальных итерациях наблюдается резкое уменьшение функционала. Затем разность между предыдущим и текущим значениями функционала уменьшается, и получаемые значения от итерации к итерации отличаются мало. Это говорит о том, что функционал в окрестности искомых значений близок к линейной форме, что подтверждает и метод Ньютона – Гаусса, так как частные производные радиальной скорости по искомым параметрам очень малы.
Получаемая в ходе работы алгоритма минимизации функционала методом Ньютона – Гаусса нормальная система линейных урав-
170
нений относительно невязок уточняемых параметров имеет плохо обусловленную матрицу. В результате решения данной системы уравнений возникают большие численные ошибки, которые приводят к расхождению всего алгоритма в целом.
Коэффициенты матрицы линейных уравнений относительно невязок уточняемых параметров получаются как суммы соответствующих частных производных минимизируемого функционала по уточняемым параметрам. Поэтому плохая обусловленность данной матрицы может объясняться:
1)параметрами выбранной орбиты, выбором рабочих витков;
2)методом вычисления самих частных производных.
Для проверки первой из выдвинутых гипотез были рассчитаны параметры другой орбиты: наклонение 60 град., высота 500 км, тип
– круговая, радиус орбиты r = 6871160 м, скорость V = 7616.51 м/с, период обращения P = 5668.3099 с.
Начальные условия в мгновенной системе координат, связанной с невращающейся Землей, принимаемые за истинные, таковы: x = 6871160, y = 0, z = 0, Vx = 0, Vy = 3808.257, Vz = 6596.096.
Соответствующие им начальные условия для данной орбиты в мгновенной системе координат, связанной с вращающейся Землей, принимаемые за истинные для данной орбиты таковы: x = 6871160, y = 0, z = 0, Vx = 0, Vy = 3307.209949041, Vz = 6596.096063867.
Координаты наблюдательного пункта в мгновенной системе ко-
ординат: xнп = 451063572, yнп = –4510634.157, zнп = 0.
Чтобы исключить влияние выбора витков на алгоритм, в модели использована полная группа измерений – принято допущение о том, что измерения ведутся непрерывно в течение двух суток полета КА. Также принято допущение о том, что измеренные значения точные.
На построенной модели алгоритм минимизации функционала методом Ньютона – Гаусса вновь разошелся.
Численное дифференцирование является одной из самых неточных вычислительных операций. Поэтому от метода нахождения производной от функции многое зависит. В предложенном алгоритме вычисление частных производных велось по формулам
(2.142).
171
Вычислим производные по упрощенной схеме |
|
||||
|
D |
|
D D0 |
, |
(2.156) |
|
qi |
|
|||
|
|
qi q0i |
|
||
где D – значение радиальной скорости, вычисленной для траектории с возмущенной координатой qi = qi0 + q.
При таком способе вычисления частных производных и при вышеуказанных допущениях для имитационной модели предлагаемый алгоритм сходится в некоторой области начальных условий к истинным значениям уточняемых параметров. Причем сходимость наблюдается для обеих тестовых орбит.
В выражениях (2.142) присутствуют и операции извлечения корня, и операции деления, численные реализации которых приводят к росту вычислительных погрешностей. Учитывая, что при формировании матрицы линейных относительно невязок уточняемых параметров уравнений используется от 500 до 1000 измерений, накопление вычислительной ошибке критично сказывается на конечном результате. Упрощенная схема позволяет уменьшить вычислительную погрешность, и поэтому, как и ожидалось, алгоритм начинает работать.
Алгоритм сходится в некоторой окрестности начальных условий, когда погрешности по составляющим скорости не превышают нескольких десятков километров в секунду, а по координатам – несколько тысяч метров. Причем сходимость наблюдается и для физически реализуемой тестовой модели, т.е. если выбрать видимые с НП участки витков, которые расположены под углом места, приблизительно равным 90о к НП. Для нормальной работы алгоритма на данной тестовой модели достаточно четырех витков, причем два из них должны быть восходящими, а два – нисходящими.
2.5. Использование метода линеаризации при решении задач перехвата средств воздушного нападения
При решении штурманских задач истребительной авиации, направленных на расчет параметров траектории полета истребителя, возникают задачи минимизации углубления воздушных средств нападения противника на охраняемую территорию [39]. Как прави-
172
ло, это – сложные задачи нелинейного программирования при наличии нелинейных ограничений. Ниже предлагается метод расчета одной из таких задач, основанный на линеаризации исходных критерия и ограничений относительно текущей точки итерационного процесса минимизации. Прежде всего, рассмотрим классический профиль полета истребителя.
2.5.1.Особенности полета истребителя. Профиль полета
Вобобщенном случае вертикальный профиль полета летательного аппарата (ЛА) представляет собой полет «по потолкам». Характерный вид такого профиля полета представлен на рис. 2.12.
Рис. 2.12. Вертикальный профиль полета ЛА
Производя полет по такой траектории, ЛА достигает наиболее рационального сочетания расход топлива – скорость. На рис. 2.12 обозначены участки вертикального профиля полета ЛА:
1) взлет – взлет ЛА с аэродрома и первоначальный набор высоты. Участок характеризуется временем взлета Tвзл , путем, который
при этом преодолевает ЛА Sвзл , и топливом, необходимым на взлет Gвзл ;
2)первый набор – полет ЛА до высоты крейсерского участка,
участок описывается функциями Tн1(H), Sн1(H), Gн1(H) – время, путь, топливо в зависимости от высоты, на которой находится ЛА;
3)крейсерский участок – горизонтальный полет на высоте Hкр наименьших затрат топлива, для этого участка известен секундный расход топлива gкр и скорость vкр;
173
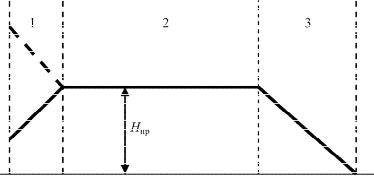
4)разгон – участок, на котором ЛА преодолевает звуковой барьер и набирает скорость, необходимую для полета на балансном участке; в дальнейшем время, путь и затрачиваемое топливо на разгон будем обозначать Tр, Sр, Gр соответственно;
5)второй набор – полет ЛА до высоты балансного участка Нбал. Участок полностью определен функциями Tн2(H), Sн2(H), Gн2(H);
6)балансный участок – полет по горизонтали с одной из программных скоростей на высоте Нбал с секундным расходом топлива
gбал;
7) снижение – на данном участке ЛА снижается до рекомендо-
ванной высоты Hат; известны функции Tсн(H), Sсн(H), Gсн(H) и vсн(H) – время, путь, расходуемое топливо и скорость соответст-
венно в зависимости от высоты на участке снижения;
8)конечный участок – полет по горизонтали на высоте Нат и на скорости vат = vсн(Нат) в течение заранее заданного интервала времени Tат (порядка 30 с); известен секундный расход топлива gат(Нат); в конце этого участка производится применение оружия;
9)применение оружия – ракета, оснащенная головкой самонаведения, летит до поражения ВО с заранее известной средней скоро-
стью vрак, также известна предельная упрежденная дальность пуска ракеты D.
После применения оружия (пуска ракеты), ЛА возвращается на аэродром. Полет на аэродром (привод) проходит с более простым вертикальным профилем (рис. 2.13).
Рис. 2.13. Профиль полета истребителя на приводе
174
Вертикальный профиль полета на приводе состоит из следующих участков:
1)набор или снижение – это участок, на котором происходит
набор или снижение до высоты привода Нпр и который характеризуется величинами Tн пр(Нат), Sн пр(Нат), Gн пр(Нат);
2)крейсер привода – полет по горизонтали на высоте Нпр со ско-
ростью vпр и с наименьшим километровым расходом топлива qпр; 3) снижение до аэродрома – снижение и посадка ЛА на аэро-
дром. Участок характеризуется временем снижения Tсн пр, путем, который истребитель преодолевает при снижении Sсн пр, и затрачиваемым на снижение и посадку топливом Gсн пр + Gпос.
2.5.2. Модель движения истребителя
Прежде чем перейти к изложению алгоритма, необходимо прокомментировать упрощения, к которым пришлось прибегнуть для построения математической модели.
1.Воздушный объект (ВО) движется равномерно по большому кругу Земли. Это – серьезное допущение, но единственно возможное предположение, которое мы можем сделать. Это допущение сделано на том основании, что для совершения маневра, особенно в вертикальной плоскости, требуются колоссальные затраты топлива. Следовательно, логично предположить, что ВО движется прямо к месту своего назначения по кратчайшему пути, то есть по большому кругу.
2.Та часть земной поверхности, над которой движутся ВО и ЛА, считается сферой. Так как радиус действия авиации и дальность обнаружения ВО сравнительно невелики, то полученное решение будет незначительно отличаться от решения с учетом истинной формы земной поверхности.
3.Аэродромы взлета и посадки совпадают. Это допущение обеспечивает линейность ограничения по топливу (см. ниже). Кроме того, такая ситуация является наиболее распространенной.
Геометрическая интерпретация задачи представлена на рис. 2.14, где С – точка с координатами ( ц, ц), в которой обнаружен ВО, А – точка ( п, п) – аэродром, на котором дислоцирован ЛА, В – прогнозируемая точка встречи с неизвестными координатами ( у, у).
175

Рис. 2.14. Геометрия задачи на сфере
Тогда начальное расстояние между ВО и ЛА можно найти по формуле [49]:
R0 Rз arccos(sin( ц )sin( п ) cos( ц )cos( п )cos( ц п )),(2.157)
где Rз – радиус Земли.
При определении угла 0 между вектором скорости ВО и линией визирования возникают некоторые сложности. Обозначим угол OCA в сферическом треугольнике . Тогда
|
|
|
|
R |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
sin( п ) sin( ц )cos |
|
|
|
|
|
||
arccos |
|
|
Rз |
|
. |
(2.158) |
||
|
|
|
|
|
|
|||
|
R0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
cos( ц )sin |
|
|
|
|
|
|||
|
Rз |
|
|
|
|
|
|
|
Обозначим ц – курс ВО (угол, отсчитываемый по часовой стрелке от северного направления меридиана к вектору скорости
ВО. Тогда, если 0 ц , то
0 |
ц |
. |
(2.159) |
В противном случае выражение для 0 имеет различный вид в зависимости от взаимного положения ЛА и ВО, а также от соотношений между углами ц и .
176
Учитывая вышесказанное, начальный угол 0 между вектором скорости ВО и линией визирования наиболее просто можно определить следующим образом. Предположим, что в течение некоторого достаточно большого времени TD ВО беспрепятственно продолжит полет. Тогда через указанное время ВО окажется в некоторой точке D (см. рис. 2.14), координаты которой ( D, D) несложно определить, используя формулы сферической геометрии:
|
|
|
|
|
|
|
|
v |
ц |
T |
D |
|
|
|
|
|
|
v |
ц |
T |
D |
|
|
|
|
|
|||
|
D |
arcsin sin( |
ц |
)cos |
|
|
|
cos( |
ц |
)sin |
|
|
cos( |
ц |
) |
,(2.160) |
|||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
Rз |
|
|
|
|
|
|
|
Rз |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v T |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin |
ц |
D |
sin( ц ) |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
D |
|
ц |
arcsin |
|
|
Rз |
|
|
|
|
|
|
, |
|
|
(2.161) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
cos( D ) |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где vц – скорость ВО. Пусть a – расстояние между точками С и D, a b – расстояние между A и D. Тогда угол 0 определяется по формуле
|
cos(b/ R |
з |
) cos(R |
0 |
/ R )cos(a/ R |
з |
) |
|
||
0 |
|
|
|
з |
|
|
(2.162) |
|||
arccos |
sin(R0 / Rз )sin(a/ Rз ) |
|
|
. |
||||||
|
|
|
|
|
|
|||||
Как видим, полученное выражение (2.162) включает в себя параметры a и b, которые зависят от произвольно выбранного времени TD. Однако из рис. 2.14 видно, что a и b взаимосвязаны таким образом, что при любом выборе TD значение 0 остается постоянным. Предложенный способ расчета 0 является математическим приемом, позволяющим упростить вычисления.
Используя формулы сферической геометрии, из треугольника ABC найдем расстояние Sг(Tц), пройденное ЛА с момента взлета до применения оружия, и путь, пройденный ракетой:
|
|
|
|
|
|
|
|
|
R |
0 |
|
v |
T |
|
|
||||
S |
г |
(T ) R |
з |
arccos cos |
|
|
cos |
|
ц ц |
|
|
||||||||
|
|
|
|
|
|||||||||||||||
|
ц |
|
|
|
|
|
|
Rз |
|
|
|
Rз |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
R |
0 |
|
v |
T |
|
|
|
|
|
|
|
|
|
|||
|
|
sin |
|
|
sin |
|
ц ц |
cos( |
0 |
) , |
|
(2.163) |
|||||||
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
Rз |
|
|
Rз |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
177
где Tц – время перехвата ВО, которое необходимо минимизировать, а R0 и 0 определяются по формулам (2.157) и (2.161) соответственно.
Для поражения цели летательным аппаратом необходимо и достаточно выполнение следующих условий.
Время движения цели Tц и время полета перехватчика Тп совпадают:
Tц Tп . |
(2.164) |
Горизонтальная проекция вертикального профиля полета Sв и расстояние Sг(Tц), пройденное ЛА по дуге большого круга, совпадают:
Sв Sг (Tц ). |
(2.165) |
Оставшиеся два условия тривиальны и определяют остаток топлива и время движения цели соответственно:
Gост 0, |
(2.166) |
Tц 0. |
(2.167) |
Время движения ЛА по участкам вертикального профиля полета равно:
Tп Tпас Tрегл Tвзл Tн1(Hкр ) Tкр Tр Tн2 (Нбал ) |
(2.168) |
Tбал Tсн (Hат ) Tат (D/vрак ), |
|
где Tпас – пассивное время ожидания на аэродроме, которое необходимо определить в ходе решения задачи; Tрегл – регламентное время (время подготовки ЛА к взлету заранее известно, зависит от типа самолета); Tкр – время крейсерского полета, которое необходимо определить в ходе решения задачи; Tбал – время полета на балансном участке, которое необходимо определить в ходе решения задачи.
Введем обозначение
Tсум Tрегл Tвзл Tн1(Hкр ) Tр Tн2 (Нбал )
Tсн (Hат ) Tат (D/vрак );
(2.169)
Tсум – суммарное время движения ЛА на детерминированных уча-
стках.
Тогда с учетом (2.169) условие (2.168) примет вид
178
|
|
Tп Tсум Tпас Tкр Tбал. |
|
|
|
|
(2.170) |
|||||||||
Путь Sв, который преодолевают ЛА при движении по участкам |
||||||||||||||||
вертикального профиля полета, равен: |
Sр |
Sн2(Hбал ) |
|
|
||||||||||||
|
Sв Sвзл Sн1(Hкр ) vкрTкр |
|
(2.171) |
|||||||||||||
|
|
vбалTбал |
Sсн (Hат ) vатTат D. |
|
|
|
||||||||||
|
|
|
|
|
|
|||||||||||
Обозначив |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Sсум Sвзл Sн1(Hкр ) Sр Sн2 (Hбал ) |
|
|
||||||||||||
|
|
|
Sсн (Hат ) vатTат D , |
|
|
|
|
(2.172) |
||||||||
где Sсум – путь, пройденный ЛА на детерминированных участках, |
||||||||||||||||
перепишем (2.171) следующим образом: |
|
|
|
|
|
|
||||||||||
|
|
Sв Sсум |
vкрTкр vбалTбал . |
|
|
|
(2.173) |
|||||||||
Остаток топлива Gост |
после перехвата и привода на аэродром |
|||||||||||||||
рассчитывается по формуле |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
G G G |
(H |
кр |
) g T G G |
(H |
бал |
) |
|
||||||||
|
|
зап |
взл |
н1 |
|
|
|
кр |
кр |
р |
н2 |
|
|
|
||
G G |
gбалTбал Gсн(Hат ) gатTат |
Gнпр (Hат) |
|
, (2.174) |
||||||||||||
ост |
|
G |
G |
q (S |
сум |
D v T |
v |
T |
|
|
||||||
|
|
снпр |
пос |
|
пр |
|
|
|
кр кр |
бал бал |
|
|
||||
|
|
|
|
Sнпр (Hат ) Sснпр) |
|
|
|
|
|
|||||||
где G – полный запас топлива; Gзап – запас топлива, учитывающий погрешность расчета времени пути и топлива на детерминированных участках.
Введем обозначение Gсум – топливо, необходимое ЛА для преодоления детерминированных участков:
|
Gзап Gвзл Gн1(Hкр ) Gр Gн2(Hбал ) |
|
|
|
|
|
|
Gсум Gсн (Hат ) gатTат Gнпр (Hат ) Gснпр Gпос |
(2.175) |
||
|
qпр (Sсум D Sнпр(Hат ) Sснпр ) |
|
|
|
|
|
|
|
|
|
|
и, сгруппировав расход топлива на детерминированных участках, перепишем (2.174) в более простом виде:
Gост (G Gсум ) [(gкр qпрvкр )Tкр (gбал qпрvбал )Tбал ].(2.176)
179
Учитывая вышеизложенное, получаем необходимые и достаточные условия перехвата ВО:
Tц Tсум Tпас Tкр Tбал ; |
(2.177) |
|
Sсум vкрTкр vбалTбал Sг (Tц ); |
(2.178) |
|
Gост (G Gсум ) [(gкр qпрvкр )Tкр (gбал |
qпрvбал )Tбал ];(2.179) |
|
Tц 0, Tпас 0, Tкр 0, Tбал 0, |
Gост 0, |
(2.180) |
где Sг(Tц) = Sв и определяется по формуле (2.173).
2.5.3. Задача определения минимального времени перехвата
Критерием качества, обеспечивающим минимальное время перехвата, является критерий вида
J(Tпас, Tкр, Tбал, Tц, Gост) = –Tц.
Максимум этого критерия, удовлетворяющий условиям (2.177) – (2.180), является искомым минимальным временем перехвата.
Таким образом, определить минимальное время перехвата ВО Tц, оптимальное пассивное время Tпас, оптимальные времена Tкр, Tбал и остаток топлива Gост можно, решив нелинейную задачу условной минимизации: найти
max{J(Tпас,Tкр ,Tбал ,Tц ,Gост ) Tц}
при ограничениях
Tц Tсум Tпас Tкр Tбал; |
|
|||
S |
v T v T |
S (T ); |
|
|
сум |
кр кр |
бал бал |
г ц |
(2.181) |
|
(G Gсум) [(gкр qпрvкр)Tкр (gбал qпрvбал)Tбал]; |
|||
Gост |
|
|||
|
0,Tкр |
0,Tбал 0,Tц 0,Gост 0. |
|
|
Tпас |
|
|||
Для решения исходной задачи (2.181) нелинейного программирования (НЛП) разложим нелинейную функцию Sг(Tц) в ряд Тейлора вблизи некоторой начальной точки Тц0 и, отбросив все члены выше первого порядка, получим следующую задачу линейного программирования (ЛП): найти
max{J(Tпас,Tкр ,Tбал ,Tц ,Gост ) Tц}
180

при ограничениях
T T |
T |
|
T T ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
ц |
сум |
пас |
|
|
|
|
кр |
|
|
бал |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Sсум |
vкрTкр vбалTбал |
Sг (Tц0) Sг (Tц0)(Tц |
Tц0 ); |
|
|
|
|
|
|
(2.182) |
||||||||||||||||||||||||||||||||||||||||
|
(G Gсум ) [(gкр qпрvкр )Tкр |
|
(gбал |
qпрvбал)Tбал ]; |
|
|||||||||||||||||||||||||||||||||||||||||||||
Gост |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,Gост |
0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Tпас 0,Tкр 0,Tбал 0,Tц |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
v T |
|
|
|
R |
|
|
|
|
|
v T |
|
|
R |
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
v sin |
|
|
|
ц ц |
|
|
cos |
|
|
|
|
0 |
|
|
cos |
|
|
|
ц ц |
|
|
sin |
|
|
|
|
0 |
|
|
cos( ) |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
ц |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|||||||||||||||||||||
Sг (Tц) |
|
|
|
|
|
Rз |
|
|
|
Rз |
|
|
|
Rз |
|
|
|
Rз |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|||
|
|
|
|
|
|
vцTц |
|
|
|
|
|
|
|
|
R0 |
|
|
|
|
|
|
|
vцTц |
|
|
|
|
|
|
R0 |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
1 cos |
cos |
sin |
sin |
cos( |
|
) |
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
Rз |
|
|
Rз |
|
|
Rз |
|
|
|
Rз |
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2.183) |
|||||
– первая |
|
производная функции Sг(Tц). Вторая производная этой |
||||||||||||||||||||||||||||||||||||||||||||||||
функции имеет вид |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R0 |
|
|
|
|
|
|
R0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
R |
|
1 cos2 |
|
|
|
|
sin2 |
|
|
|
cos2 ( |
|
) |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
з |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
Rз |
|
|
|
|
|
|
Rз |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 . |
|
||||
Sг (Tц) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|||
|
|
R0 |
|
cos |
|
vцTц |
|
|
sin |
|
R0 |
|
sin |
vцTц |
cos( |
2 |
|
|
||||||||||||||||||||||||||||||||
|
1 |
cos |
|
|
|
|
) |
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
R |
R |
|
|
|
|
|
R |
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
0 |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
з |
|
|
|
з |
|
|
|
|
|
|
|
|
|
|
з |
|
|
|
|
з |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
(2.184)
Нетрудно убедиться, что при всех значениях Tц вторая производная Sг (Tц ) неотрицательна и Sг (Tц ) 0 , т.е. функция Sг(Tц) вы-
пукла и, следовательно, допустимое множество задачи (2.181) также выпукло.
Решив задачу ЛП (2.182), получим Тц, которое используется как начальное приближение для инициализации следующей задачи ЛП. Итерационный процесс продолжается до тех пор, пока полученное Тц не удовлетворит условию:
Scум vкрTкр vбалTбал Sг (Tц ) , |
(2.185) |
где ε – заданная точность (например, = 1 м).
Задача ЛП (2.182) на каждой итерации решается двухэтапным методом (методом искусственного базиса и симплекс-методом).
181
Для этого вводятся искусственные переменные R1, R2 и новая целевая функция r = R1 + R2, которую необходимо минимизировать. Если минимум этой функции равен нулю, то исходная задача имеет допустимое решение. В данном случае вспомогательная задача принимает вид
|
|
|
|
|
|
|
|
|
|
{r(Tпас,Tкр,Tбал,Tц,Gост , R1, R2 ) (R1 R2 )} max; |
|||||||||
T |
|
T T |
T R T ; |
|
|
||||
|
пас |
кр бал |
ц |
|
1 |
сум |
|
|
|
|
|
|
|
|
|
|
|
|
|
vкрTкр vбалTбал Sг (Tц0)Tц R2 Sсум Sг (Tц0) Sг (Tц0)Tц0; |
|||||||||
G |
|
(G G |
) [(g |
кр |
q |
v )T (g |
бал |
q v )T ]; |
|
|
ост |
|
сум |
|
|
пр кр кр |
пр бал бал |
||
T |
0,T 0,T 0,G |
0, R 0, R 0. |
|||||||
|
пас |
|
кр |
ц |
|
ост |
1 |
2 |
|
(2.186)
Первый вариант расстановки знаков соответствует случаюSсум Sг (Tц0) Sг (Tц0 )Tц0 0 , в противном случае используется второй вариант. Варианты расстановки знаков обеспечивают неотрицательность соответствующего свободного члена симплекстаблицы.
Оптимальное базисное решение, полученное на первом этапе, используется в качестве начального базиса при решении задачи ЛП (2.182).
После того, как найдено оптимальное Tц,, несложно найти координаты точки уничтожения ВО ( у, у):
|
|
|
|
|
v |
T |
|
|
|
|
|
|
|
v |
T |
|
|
|
|
||
|
у |
arcsin sin( |
ц |
)cos |
|
ц ц |
|
cos( |
ц |
)sin |
|
ц ц |
cos( |
ц |
) |
; (2.187) |
|||||
|
|
|
|
||||||||||||||||||
|
|
|
|
Rз |
|
|
|
|
|
|
|
Rз |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
v |
|
T |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
ц |
ц |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
sin |
Rз |
sin( ц ) |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
arcsin |
|
|
|
|
|
|
|
|
. |
|
|
(2.188) |
|||||
|
|
|
cos( у ) |
|
|
|
|||||||||||||||
|
|
у |
|
|
ц |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Также несложно определить дальность Rлв и азимут θлв линии визирования, соединяющей аэродром взлета и точку уничтожения цели:
Rлв Rзarccos(sinφаsinφу cosφаcosφуcos (λа λу ));(2.189)
182

|
|
|
у sinφаcos |
Rлв |
|
|
|
|
|
|
||||||||
|
sinφ |
|
|
|
|
|
|
|
|
|
||||||||
|
R |
|
|
|
|
|
|
|||||||||||
arccos |
|
|
|
|
|
|
|
з |
|
, если |
λа λу; |
|||||||
|
|
|
Rлв |
|
|
|
||||||||||||
|
|
cosφаsin |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Rз |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2.190) |
||||
θлв |
|
|
|
|
|
|
|
|
|
|
|
|
|
Rлв |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
sinφу sinφаcos |
|
|
|
|
|
|
||||||||||
|
|
R |
|
|
||||||||||||||
2π |
arccos |
|
|
|
|
|
|
|
|
|
|
|
з |
|
|
, |
если λа λу. |
|
|
|
|
|
|
|
Rлв |
|
|
||||||||||
|
|
|
|
cosφаsin |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
R |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
з |
|
|
|
|
|
|
|
|
|
2.5.4. Выбор начального приближения
Немаловажным вопросом является правильный выбор начального приближения Tц0. Метод Ньютона в данном случае гарантирует сходимость для любого начального приближения Tц0, удовлетворяющего неравенству [20]:
Sг (Tц0 )Sг (Tц0 ) (Sг (Tц0))2 . (2.191)
Очевидно, что, если в (2.191) подставить (2.173), (2.183) и (2.184), то решить полученное неравенство относительно Tц0 будет крайне затруднительно. Поэтому предлагается воспользоваться результатами решения рассматриваемой задачи при аппроксимации земной поверхности плоскостью.
Остановимся подробнее на методе определения начального приближения.
Пусть в начальный момент времени известны геоцентрические координаты (широта и долгота) аэродрома взлета и ВО. Принимая во внимание допущение о плоской Земле, перейдем от геоцентрической системы координат к ортогональной, связанной с аэродромом. Центр этой системы координат поместим в точку, соответствующую аэродрому взлета, ось Х направим по меридиану на север, ось Y – на восток, перпендикулярно оси Х. Тогда, начальные координаты ВО будут – (xц0, yц0), и начальное расстояние между ВО и ЛА можно рассчитать по формуле:
R0 |
|
|
|
|
xц20 yц2 |
0 , |
(2.192) |
||
183
при этом начальный угол 0 между вектором скорости ВО и линией визирования определяется по формуле:
|
|
|
|
xц0cos( ц) yц0 sin( ц) |
|
|
|
0 |
arccos |
|
|
. |
(2.193) |
|
||||||
|
|
|
R0 |
|
|
|
|
|
|
|
|
|
|
Тогда расстояние Sг(Tц), которое при сферической Земле рассчитывалось по формуле (2.163), можно рассчитать по теореме косинусов:
|
|
|
|
|
Sг (Tц ) |
R02 (vцTц )2 |
2R0vцTц cos ( 0 ) . |
(2.194) |
|
В остальном постановка задачи и метод ее решения ничем не отличаются от задачи для сферической Земли.
Подставляя в неравенство (2.191) значение Sг (Tц ) , вычислен-
ное по формуле (2.194), и соответствующие этой формуле производные Sг (Tц ) и Sг (Tц0), получим решение неравенства (2.191):
T |
|
R0 sin( 0) |
, |
(2.195) |
|
||||
ц0 |
|
vц |
|
|
|
|
|
||
которое используется в качестве начального приближения для задачи (2.179) с учетом сферичности Земли.
2.5.5. Тестовые примеры задач перехвата по минимальному углублению цели
Рассмотрим тестовый пример для задачи «Перехват по минимальному углублению цели», алгоритм решения которой изложен ранее.
В качестве примера выбран некоторый гипотетический ВО, который летит на высоте 10 км, со скоростью 300 м/c и курсом 90 град., также выбран некоторый гипотетический тип ЛА. Результаты решения задачи перехвата цели по минимальному углублению в зависимости от начальных значений R0 и 0 представлены в табл. 2.7.
На рис. 2.15 схематично представлены взаимные положения аэродрома, на котором базируется истребитель, и цели в начальный момент для некоторых ситуаций, приведенных в таблице (цифры на рисунке соответствуют номерам строк таблицы).
184
В ситуациях 1-14 ЛА успевает перехватить ВО в передней полусфере атаки до того, как ВО попадает в «запретный цилиндр».
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 2.7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Начальные |
|
|
Оптимальные решения |
|
|
|
|
Область |
||||||
|
|
|
условия |
|
|
|
|
|
|
||||||||
|
№ |
|
|
|
|
|
|
|
|
|
|
|
|
пораже- |
|||
|
|
R0, |
|
0, |
|
|
|
|
|
|
|
|
|
Gост, |
|
||
|
|
|
|
Tц, с |
|
Tпас, с |
Tкр, с |
|
|
Tбал, с |
|
|
|
ния |
|||
|
|
|
км |
|
град |
|
|
|
|
|
|
|
|
|
кг |
|
|
|
1 |
|
1790 |
|
4,5 |
3250 |
|
253 |
2107 |
|
|
0 |
|
|
0 |
|
ППС |
2 |
1755 |
4,3 |
3131 |
135 |
2107 |
|
0 |
|
|
0 |
|
ППС |
|||||
3 |
1712 |
3,9 |
2988 |
0 |
2096 |
|
3 |
|
|
0 |
|
ППС |
|||||
4 |
1625 |
3,3 |
2802 |
0 |
1853 |
|
60 |
|
|
0 |
|
ППС |
|||||
5 |
1495 |
2,3 |
2524 |
0 |
1490 |
|
145 |
|
|
0 |
|
ППС |
|||||
6 |
1408 |
1,5 |
2340 |
0 |
1249 |
|
201 |
|
|
0 |
|
ППС |
|||||
7 |
1234 |
0,1 |
1972 |
0 |
769 |
|
314 |
|
|
0 |
|
ППС |
|||||
8 |
961 |
3,1 |
1398 |
0 |
19 |
|
489 |
|
|
0 |
|
ППС |
|||||
9 |
954 |
3,2 |
1384 |
0 |
0 |
|
494 |
|
|
0 |
|
ППС |
|||||
10 |
930 |
3,5 |
1357 |
0 |
0 |
|
467 |
|
|
202 |
|
ППС |
|||||
|
11 |
|
843 |
|
4,7 |
1257 |
|
0 |
0 |
|
|
367 |
|
|
947 |
|
ППС |
12 |
714 |
6,9 |
1109 |
0 |
0 |
|
219 |
|
|
2055 |
|
ППС |
|||||
13 |
457 |
14,1 |
846 |
0 |
0 |
|
12 |
|
|
3609 |
|
ППС |
|||||
14 |
446 |
14,6 |
835 |
0 |
0 |
|
0 |
|
|
3697 |
|
ППС |
|||||
15 |
333 |
21,0 |
1623 |
768 |
0 |
|
0 |
|
|
3697 |
|
ЗПС |
|||||
16 |
217 |
35,1 |
1167 |
333 |
0 |
|
0 |
|
|
3697 |
|
ЗПС |
|||||
17 |
171 |
47,6 |
956 |
122 |
0 |
|
0 |
|
|
3697 |
|
ЗПС |
|||||
19 |
155 |
55,0 |
867 |
32 |
0 |
|
0 |
|
|
3697 |
|
ЗПС |
|||||
20 |
132 |
74,4 |
896 |
0 |
0 |
|
6 |
|
|
3649 |
|
ЗПС |
|||||
21 |
127 |
90,0 |
1007 |
0 |
0 |
|
117 |
|
|
2822 |
|
ЗПС |
|||||
22 |
135 |
109,2 |
1155 |
0 |
0 |
|
265 |
|
|
1710 |
|
ЗПС |
|||||
23 |
155 |
125,0 |
1311 |
0 |
0 |
|
421 |
|
|
546 |
|
ЗПС |
|||||
24 |
167 |
130,8 |
1383 |
0 |
0 |
|
494 |
|
|
0 |
|
ЗПС |
|||||
1 |
|
|
|
|
14 |
|
|
16 |
17 |
|
21 |
24 |
|
|
|||
аэро- |
Sсум
Рис. 2.15. Взаимное положение аэродрома взлета и ВО в начальный момент времени
185
В ситуациях 15-16, хотя ВО и находится в начальный момент вне «запретного цилиндра», однако ЛА не успевает за время Tсум перехватить ВО в передней полусфере. Поэтому поражение происходит в задней полусфере атаки.
Ситуации 17-20 соответствуют случаю, когда ВО уже в начальный момент времени находится внутри «запретного цилиндра». Поэтому поражение возможно только в задней полусфере.
Ситуации 21-24 соответствуют случаю 0 /2, когда перехват возможен только в заднюю полусферу атаки.
Рассмотрим ситуации таблицы более подробно.
Вситуациях 1-2 истребителю приходится пассивно ожидать на аэродроме, а затем перехватывать цель на минимальной программной (крейсерской) скорости с минимальным расходом топлива. Это происходит вследствие того, что в начальный момент цель находится вне области действия истребителя.
Вслучаях 3-8 истребитель осуществляет полет и на крейсерской, и на балансной высоте, что обеспечивает минимальное суммарное углубление цели.
Вслучаях 9-13 цель находится так близко к аэродрому, что истребителю хватает топлива, чтобы лететь только на балансной высоте с максимальной скоростью. В ситуации 14 цель в момент ее перехвата находится на границе «запретного цилиндра», и наведение истребителя происходит в ППС.
Вслучаях 15-19 истребителю приходится пассивно ожидать, пока он не сможет перехватить цель в ЗПС на границе «запретного цилиндра». В ситуациях 20-24 ЛА «догоняет» цель на максимальной балансной скорости.
Результаты тестирования на гипотетических примерах показали, что приведенный выше способ задания начальных приближений, действительно обеспечивает устойчивую сходимость метода. Од-
нако если 0 0 |
|
|
и при этом возможен перехват как в перед- |
|
2 |
||||
|
|
|
нюю (ППС), так и в заднюю (ЗПС) полусферы атаки, итерации могут сойтись к большему времени перехвата в ЗПС по сравнению с меньшим временем перехвата в ППС.
186
2.6. Использование методов нелинейного программирования при оценке параметров формирующего фильтра
Важные прикладные аспекты использования методов нелинейного программирования связанны с задачами идентификации параметров систем различной природы и назначения. Одной из таких задач идентификации может служить задача определения параметров формирующего фильтра, выходом которого является случайный процесс, корреляционная функция которого близка корреляционной функции моделируемого случайного процесса. Рассмотрим, прежде всего, основные свойства формирующих фильтров.
2.6.1. Основные свойства формирующих фильтров
Как известно [50], формирующим фильтром называется линейная динамическая система (в общем случае нестационарная), на вход которой подаётся нормально распределенный «белый шум» единичной интенсивности, а выходом является случайный процесс, корреляционная функция которого Ky (t1,t2 ).
В общем случае уравнение формирующего фильтра имеет вид
an (t) |
dn y(t) |
an 1 |
(t) |
dn 1y(t) |
... a0 |
(t)y(t) |
|||||
|
dtn |
|
dtn 1 |
||||||||
|
|
|
|
|
|
|
|
|
|
||
bm (t) |
|
dm x(t) |
bm 1(t) |
dm 1x(t) |
... b0 |
(t)x(t), (2.196) |
|||||
|
dtm |
|
dtm 1 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
||
где a0 (t), , an (t),b0(t), ,bm(t) – коэффициенты формирующего фильтра (m n); y(t) – случайный процесс на выходе фильтра; x(t) – нормально распределенный «белый шум» интенсивности
Nx .
Уравнение (2.196) можно записать в операторной форме:
Dn (S,t)y(t) Mm(S,t)x(t), |
(2.196а) |
где Dn(S,t) и Mm(S,t) – линейные операторы: |
|
Dn (S,t) an(t)Sn a0 (t); |
(2.197а) |
Mm (S,t) bm (t)Sm b0(t). |
(2.197б) |
187
Как известно, корреляционная функция Ky (t1,t2 ) произвольного случайного процесса y(t) определяется как [7]
Kу (t1,t2 ) M[(y(t1) mу (t1))(y(t2) mу (t2 ))], |
(2.198) |
где my (ti ) – математическое ожидание сечения случайной функ-
ции y(t) в момент ti .
Известно, что корреляционная функция обладает следующими свойствами.
1. Ky (t1,t2) Ky (t2,t1) – свойство симметрии.
2. K |
2 |
(t ,t |
2 |
) K |
y |
(t ,t )K |
y |
(t |
2 |
,t |
2 |
). |
(2.199) |
|
y |
1 |
|
1 1 |
|
|
|
|
3. Ky (t1,t2 ) – положительно определенная функция.
Предположим, что импульсная переходная функция динамической системы (2.196), представляющая собой реакцию этой системы на бесконечно большой импульс, поданный в момент времени, известна:
|
k(t, ) |
Mm (S,t) |
(t ), |
t ; |
|
|||
|
|
(2.200) |
||||||
|
|
|
Dn (S,t) |
|
|
|||
|
|
k(t, ) 0, |
t . |
|
|
|||
Тогда для любого момента времени t справедливо выражение |
||||||||
|
|
|
|
t |
|
|
|
|
|
|
y(t) x( )k(t, )d . |
|
(2.201) |
||||
|
|
|
|
|
|
|
|
|
Подставляя (2.201) в формулу (2.198), получим |
|
|||||||
|
|
Kу (t1,t1) M[y(t1)y(t2)] |
|
|||||
t1 |
|
t2 |
|
|
|
|
|
|
|
k(t1, 1) k(t2, 2 )Kx ( 1, 2)d 2 d 1, |
(2.202) |
||||||
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
где Kx (t1,t2 ) |
– |
корреляционная |
функция случайного |
процесса |
||||
x(t) . |
|
|
|
|
|
|
|
|
При t1 t2 |
t |
получим дисперсию процесса y(t) |
в момент |
|||||
времени t : |
|
t |
t |
|
|
|
||
2у (t) |
|
|
|
|||||
k(t, 1) |
k(t, 2)Kx ( 1, 2 ) d 2d 1 . |
(2.203) |
||||||
|
|
|
|
|
|
|
||
188
Найдем корреляционную функцию сигнала y(t) на выходе ди-
намической системы (2.196), на вход которой подается «белый шум» x(t) . Так как спектральная плотность «белого шума» посто-
янна и равна интенсивности, т.е.
Sx ( ) Sx (0) Nx, |
, |
(2.204) |
то корреляционную функцию случайного процесса x(t) можно записать в виде
|
Nx |
|
|
|
Kx ( ) |
e j d Nx ( ). |
(2.205) |
||
|
||||
|
2 |
|
||
Таким образом, корреляционная функция стационарного «белого шума» для интервала времени 1 2 будет иметь вид
Kx ( 1 2 ) Nx ( 1 2). |
(2.206) |
Подставляя (2.206) при Nx 1 в формулу (2.202), получим:
|
t1 |
t1 t2 ; |
|
Kу (t1,t2 ) |
k(t1, 1)k(t2, 1)d 1 , |
(2.207а) |
|
|
|
|
|
|
t2 |
t1 t2 . |
|
Kу (t1,t2 ) |
k(t1, 2 )k(t2, 2 )d 2 , |
(2.207б) |
Полагая в (2.207а) и (2.207б) t1 t2 t , найдем дисперсию выходного сигнала:
2y |
|
t |
2(t, )d . |
|
|
k |
(2.208) |
Для стационарных линейных динамических систем импульсная передаточная функция k(t, ) зависит только от промежутка вре-
мени, истекшего с момента подачи возмущающего импульса, т.е.
k(t, ) k(t ). |
(2.209) |
Применим к обеим частям равенства (2.207б) линейный оператор Dn(S,t) , определяемый выражением (2.197а). Тогда с учетом выражения (2.200) получим:
189
|
t2 |
|
t2 t1. (2.210) |
Dn (S,t)Ky (t1,t2) |
k(t2, )M(S,t1) (t1 |
)d ; |
Так как -функция в правой части (2.210) не равна нулю только при t1, а верхний предел t2 t1, то справедливо выражение:
Dn (S,t)Ky (t1,t2) 0, |
t2 t1, |
(2.211) |
или, подставляя значение линейного оператора (2.197а), получим линейное однородное уравнение, которому удовлетворяет корреля-
ционная функция Ky (t1,t2 ) |
при t2 t1: |
|
|
|
|
|
|
|
|||||||||||||
a |
n |
(t |
) |
dn |
K |
|
(t ,t |
|
) a |
|
(t )K |
|
(t |
|
,t |
|
) 0; |
t |
|
t . (2.212) |
|
dtn |
|
|
|
|
|
|
|
||||||||||||||
|
1 |
|
|
y |
1 |
2 |
|
|
0 |
1 |
y |
|
1 |
|
2 |
|
|
2 |
1 |
||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рассмотрим выражение (2.207а). Очевидно, что это выражение можно трактовать как уравнение свертки [50] линейной динамиче-
ской системы с импульсной переходной функцией k(t1, ) , на вход которой подается сигнал k(t2, ), а выходом является корреляционная функция Ky (t1, ). Таким образом, можно записать:
|
a |
n |
(t |
|
|
) |
dn |
K |
|
|
(t |
|
|
,t |
|
) ... a |
|
(t |
)K |
|
(t ,t |
|
|
) |
||||||||
|
|
|
dtn |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
1 |
|
|
|
у |
|
|
1 |
|
2 |
|
0 |
1 |
|
|
у |
1 |
2 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dm |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
) , t |
|
|
t . (2.213) |
|||
b |
m |
(t |
|
|
) |
|
|
|
|
k(t |
|
|
,t |
|
) ... b (t |
)k(t |
|
,t |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
1 |
|
|
dt1m |
|
1 |
|
|
2 |
|
|
|
0 1 |
|
|
1 |
|
2 |
|
|
2 |
1 |
||||||||
Рассуждая аналогичным образом, получим еще два уравнения:
an |
(t2 ) |
dn |
Kу (t1 |
,t2) ... a0(t2 )Kу (t1,t2) 0 , |
|
t1 t2 . |
(2.214) |
|||||||||||||||||||
dt2n |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
a |
n |
(t |
|
) |
dn |
K |
|
(t |
|
,t |
|
) ... a |
|
(t |
|
)K |
|
(t ,t |
|
) |
|
|||
|
|
|
dt2n |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
2 |
|
|
у |
|
1 |
|
2 |
|
0 |
|
2 |
|
у |
1 |
|
2 |
|
|
||||
|
bm (t |
2 ) |
dm |
|
k(t1,t2) ... b0 (t2)k(t1,t2) , |
t1 t2 . |
(2.215) |
|||||||||||||||||||
|
dt2m |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
190
Известно [40], что импульсная переходная функция k(t, ) линейной стационарной динамической системы при M(S, ) 1 совпадает с функцией Грина и равна:
|
|
|
|
k(t, ) G(t, ), |
|
|
|
|
|
|
|
|
(2.216) |
||||||||||
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
(t) |
|
|
|
|
2 |
(t) |
|
... |
|
|
n |
(t) |
|
|
||||
|
( 1)n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
G(t, ) |
|
1( ) |
|
|
|
2 ( ) |
|
... |
|
n ( ) |
|
; (2.217) |
|||||||||||
|
det |
1( ) |
|
|
|
2 ( ) |
|
... |
|
n ( ) |
|
||||||||||||
( ) |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
(n 2) |
( ) |
|
(n 2) |
( ) ... |
|
(n 2) |
|
|
|
|||||||||||
|
|
|
1 |
|
|
|
1 |
|
|
|
1 |
|
|
( ) |
|
||||||||
( ) – определитель Вронского: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
1 |
( ) |
|
... |
|
|
n |
( ) |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
1( ) |
|
... |
|
n ( ) |
|
|
|
|
|
(2.218) |
|||||||||
|
( ) det |
|
|
... |
|
|
... |
|
|
... |
|
, |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
(n 1) |
|
|
|
|
|
(n 1) |
|
|
|
|
|
|
|||||||
|
|
|
|
|
( ) ... |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
1 |
|
|
|
1 |
|
|
( ) |
|
|
|
|
|
||||||||
1( ),..., 2 ( ) – фундаментальное решение однородного дифференциального уравнения:
an (t) |
dn y(t) |
an 1 |
(t) |
dn 1y(t) |
... a0 |
(t)y(t) 0 |
. (2.219) |
|
dtn |
dtn 1 |
|||||||
|
|
|
|
|
|
2.6.2. Корреляционная функция формирующего фильтра второго порядка
Используя свойства корреляционной функции формирующего фильтра, полученные в п. 2.6.1, найдем в явном виде выражение для корреляционной функции случайного процесса на выходе стационарного формирующего фильтра второго порядка при
M(S, ) 1.
Вэтом случае уравнение формирующего фильтра имеет вид
d2 |
|
d |
|
|
|
|
|
y(t) a |
|
y(t) a |
|
y(t) (t). |
(2.220) |
dt2 |
|
|
||||
1 |
dt |
0 |
|
|
||
191
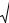
На основании свойства (2.212) корреляционная функция слу-
чайного процесса |
y(t) |
|
на выходе формирующего фильтра (2.220) |
||||||||||||||||||||||||||||||||
удовлетворяет уравнению |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
d |
2 |
K |
|
(t ,t |
|
) a |
|
d |
K |
|
(t |
|
,t |
|
) a |
|
K |
|
(t |
|
|
,t |
|
) 0; |
t |
|
t |
|
. |
|||||
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
2 |
|
y |
1 |
2 |
|
1 dt1 |
|
y |
|
1 |
|
2 |
|
|
0 |
|
y |
|
1 |
|
|
2 |
|
|
|
1 |
|
2 |
|
|||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Пусть 1, 2 – корни характеристического уравнения |
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
||||
|
|
|
|
|
a a |
|
0 ; |
|
|
|
|
|
|
a |
|
|
|
a |
|
|
4a |
|
. |
|
(2.221) |
||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
1 |
|
|
0 |
|
|
|
|
|
1,2 |
|
|
|
|
1 |
|
|
|
|
1 |
|
|
0 |
|
|
|
|
|
|||
Тогда фундаментальное решение будет иметь вид: |
|
|
|
|
|
|
|||||||||||||||||||||||||||||
1) действительные корни характеристического уравнения |
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
1(t) e 1t ; |
|
2 (t) e 2t |
; |
|
|
|
|
|
|
|
(2.222) |
|||||||||||||||||
2) кратные корни характеристического уравнения |
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
1(t) e t; |
|
2(t) te t ; |
|
|
|
|
|
|
|
(2.223) |
||||||||||||||||||
3) комплексные корни характеристического уравнения |
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
1,2(t) e 1t (cos j sin j ) . |
|
|
|
|
|
(2.224) |
||||||||||||||||||||||
Получим значение корреляционной функции для каждого вида корней характеристического уравнения.
1. Случай действительных корней. В этом случае согласно со-
отношениям (2.217) и (2.218) определитель Вронского и импульсная переходная функция будут иметь вид
( ) |
|
e 1 |
|
|
e 2 |
e |
( |
|
) |
( 2 |
1); |
(2.225) |
||||||||
1e 2 |
2e 1 |
|
1 |
|
2 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
G(t, ) |
|
|
1 |
|
|
|
|
e 1t |
e 2t |
|
|
e 1 (t ) e 2 (t ) |
k(t, ). |
|||||||
|
|
|
|
|
|
|
||||||||||||||
e |
( |
) |
( |
|
) |
|
|
|
|
|
|
|
|
|
||||||
|
1 2 |
|
2 |
|
e 1 |
e 2 |
|
|
|
|
|
|
2 |
|
||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
||
(2.226)
Подставляя в формулу (2.207а) выражение для импульсной переходной функции (2.226) и учитывая, что для стационарного случайного процесса корреляционная функция зависит только от разности моментов времени t , получим
Kу ( t) |
[ 2 exp ( 1 t) 1 exp ( 2 t)] |
. |
(2.227) |
|
|||
|
2a1a0( 2 1) |
|
|
192
2. Случай кратных корней. Для случая кратных корней определитель Вронского и импульсная переходная функция будут иметь вид
|
|
|
|
( ) |
e |
e |
|
|
e2 ; |
|
(2.228) |
||||||||
|
|
|
|
|
|
e |
e (1 ) |
|
|
|
|
|
|
||||||
G(t, ) |
1 |
|
|
e t |
te t |
|
|
e (t ) (t ) |
(t )e (t ) k(t, ). |
||||||||||
|
|
|
|||||||||||||||||
e2 |
|
|
e |
|
|
||||||||||||||
|
|
|
e |
|
|
|
e2 |
|
|
|
|
|
|
|
|
||||
Соответствующая корреляционная функция будет равна |
(2.229) |
||||||||||||||||||
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Kу ( t) exp ( t) |
|
|
|
|
|
|
. |
(2.230) |
|||||||||
|
|
2a a |
0 |
|
2a a |
0 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
||||
3. Случай комплексно-сопряженных корней. Определитель Вронского, импульсная переходная функция и корреляционная функция будут иметь вид соответственно
( ) |
|
|
a (cos jsin ) |
|
a |
(cos jsin ) |
|
|
|
||||||||||||
a |
|
|
|
|
jsin ) a |
( j)(cos jsin ) |
|||||||||||||||
|
( j)(cos |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 j e2 ; |
|
|
|
|
|
|
(2.231) |
|||||
G(t, ) |
1 |
|
e (cos t jsin t) |
|
|
e (cos t jsin t) |
|
|
|
||||||||||||
|
|
|
|
|
|||||||||||||||||
2j e2 |
|
e (cos jsin ) |
|
|
e (cos jsin ) |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
e (t ) sin ( (t )) |
; |
|
|
(2.232) |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( t) |
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
||||
Kу |
( t) e |
|
|
|
|
|
cos ( t) |
|
|
|
|
|
|
|
sin ( t) . (2.233) |
||||||
|
|
2a |
a |
|
|
2a |
0 |
a |
|||||||||||||
|
|
|
|
|
|
|
|
|
0 1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
Нетрудно показать, что вне зависимости от вида корней характеристического уравнения дисперсия стационарного случайного процесса y(t)на выходе формирующего фильтра будет одинако-
вой:
Ky (0) 2y |
1 |
|
. |
(2.234) |
2a a |
0 |
|||
|
1 |
|
|
193
2.6.3. Задача идентификации коэффициентов формирующего фильтра как задача нелинейного программирования
Как правило, для моделирования случайных процессов используются стационарные формирующие фильтры вида (2.220). При этом возникает задача идентификации коэффициентов формирующего фильтра, на выходе которого наблюдается стационарный случайный процесс y(t), корреляционная функция Ky ( t) которого
близка корреляционной функции K( t) моделируемого случайного процесса.
Вкачестве меры близости корреляционных функций истинного
имодельного случайных процессов выбран квадратичный критерий вида
|
|
|
|
J(a0,a1) (K( ) Ky (a0,a1, ))2 d . |
(2.235) |
|
0 |
|
На |
практике корреляционная функция истинного процесса |
|
K( t) |
задается в виде таблиц или графиков. В этом случае инте- |
|
гральный критерий (2.235) удобно заменить суммой квадратов невязок между корреляционными функциями истинного и модельного процессов:
N |
|
J(a0,a1) (K(i) Ky (a0,a1,i))2 . |
(2.236) |
i 1
Очевидно, что вид критерия (2.236) зависит от типа корней характеристического уравнения 1 и 2 , определяемых по формуле
(2.221):
1) действительные корни
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
T 2 |
|
|||
|
|
|
|
|
|
T |
|
2 exp |
1i |
|
|
|
1 exp |
|
2i |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
N |
|
|
|
|
|
N |
|
|
|
|
|
|
|
N |
|
||||||||
J(a |
|
,a ) |
|
K |
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
2a a |
|
|
( |
|
|
|
) |
|
|
|
|
|||||||||||
|
0 |
1 |
|
зад |
N |
|
|
|
0 |
2 |
1 |
|
|
|
|
|
||||||||||
|
|
|
i 0 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2.237)
194
2) кратные корни
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
|
2 |
|
|
N |
|
|
T |
|
|
|
|
|
|
|
|
T |
|
|
1 |
|
|
|
i |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
N |
|
||||||||||||||||||||
J(a0,a1) |
Kзад i |
|
|
|
exp |
i |
|
|
|
|
|
|
|
|
|
|
|
; |
|||||||||||
|
|
|
2a a |
|
|
|
|||||||||||||||||||||||
i 0 |
|
|
N |
|
|
|
|
|
|
N |
|
0 |
|
|
2a a |
0 |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3) комплексно-сопряженные корни |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
N |
|
|
|
|
|
T |
|
( ti) |
|
1 |
|
|
|
|
|
|
|
T |
|
||||||||
J(a0,a1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Kзад |
i |
|
e |
|
|
|
|
|
|
|
|
|
cos i |
|
|
|
|
||||||||||||
|
|
|
|
|
|
2a0a1 |
|
||||||||||||||||||||||
|
|
i 0 |
|
|
|
|
|
|
N |
|
|
|
|
|
|
|
|
|
|
|
|
N |
|
||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
T |
2 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
sin |
i |
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
2a |
|
|
N |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
0 |
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2.238)
(2.239)
где N,T – общее число точек и полный интервал времени вычисления корреляционной функции; , – действительная и мнимая
части корней характеристического уравнения.
Ясно, что задача минимизации критерия (2.236) является задачей нелинейного программирования без ограничений. Методы решения таких задач подробно описаны выше.
В конкретном случае данная задача нелинейного программирования решается двумя методами:
методом Ньютона – Гаусса; методом покоординатного спуска с одномерной минимизацией
по каждой координате.
Ниже приведены алгоритмы решения задачи этими методами.
2.6.3.1. Алгоритм решения задачи методом Ньютона – Гаусса
Метод Ньютона – Гаусса предназначен для решения задач нелинейного программирования с квадратичным критерием вида (2.236) [56], [3].
В основе данного метода лежит линеаризация нелинейной функции Ky (a0,a1,i) относительно оценок параметров на преды-
дущем шаге итерационного процесса. Основная итерационная формула имеет вид
195

|
|
cˆ |
( j) |
cˆ |
( j 1) ( т ( j) ( j)) 1 т ( j) |
e |
( j) , |
(2.240) |
|
|
a0 |
( j) |
|
|
|
|
|
где |
cˆ |
( j) a |
(j) |
– вектор оцениваемых коэффициентов на j -м |
||||
|
|
1 |
|
|
|
|
|
|
шаге итерационного процесса; ( j) – матрица производных, вы-
численная в точке оценки на предыдущем шаге итерационного процесса:
|
K (a ,a ,1) |
||||
|
у |
0 |
1 |
|
|
|
a0 |
|
|
||
|
|
|
|
||
|
|
... |
|
|
|
(j) |
|
... |
|
|
|
|
|
|
|
||
K (a ,a ,N) |
|||||
|
у |
0 |
1 |
|
|
|
|
|
a0 |
|
|
|
|
|
|
||
|
K (a ,a ,1) |
|
|
|
|||
|
у |
0 |
1 |
|
|
|
|
|
|
a1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
... |
|
|
|
. |
(2.241) |
|
|
... |
|
|
|
||
|
|
|
|
|
|
||
K (a ,a ,N) |
|
|
|||||
|
у |
0 |
1 |
|
|
|
|
|
|
a |
|
|
a0 a0(j 1), |
|
|
|
|
1 |
|
|
a a (j 1) |
|
|
|
|
|
|
|
1 |
1 |
|
В формулах (2.240), (2.241) использованы следующие обозначения:
– e( j) – вектор невязок между истинным значением корреляционной функции K(i) и корреляционной функцией Ky (a0 ( j 1);
– a1( j 1),i), соответствующей случайному процессу на выходе формирующего фильтра на ( j 1)-м шаге итерационного процесса:
|
K(1) |
Ky (a0 |
( j 1),a1 |
( j 1),1) |
|
|||
|
|
|
|
|
|
|
|
(2.242) |
e( j) |
K |
|
(a |
|
. |
|||
|
K(1) |
y |
0 |
( j 1),a |
( j 1),1) |
|
||
|
|
|
|
1 |
|
|
||
На рис. 2.16 приведена структурная схема решения задачи методом Ньютона – Гаусса.
Забегая вперед, можно отметить, что использование метода Ньютона – Гаусса обеспечивает очень быструю сходимость критерия к нулю (за две – три итерации) при задании начальных приближений вблизи точки оптимума. В противном случае, может наблюдаться расходимость итерационного процесса.
196

Рис. 2.16. Алгоритм решения задачи, метод Ньютона – Гаусса
197

Учитывая это, можно предложить следующий способ задания начальных приближений.
Воспользуемся формулой расчета дисперсии случайного процесса на выходе формирующего фильтра (2.234). Допуская, что дисперсия модельного и истинного процесса совпадают, выразим начальное приближение коэффициента a0(0) как функцию на-
чального приближения коэффициента a1(0) и значения дисперсии исходного процесса.
a0(0) |
1 |
, |
(2.243) |
2a (0) 2 |
|||
|
1 |
|
|
где 2 – значение дисперсии исходного процесса.
Пусть значения корреляционной функции исходного процесса и корреляционной функции модельного процесса также совпадают
на конце интервала расчета tf корреляционных функций, т.е. (2.244)
Здесь K(tf ) , K y(t f ) – заданная и модельная корреляционные
функции, соответственно.
Учитывая (2.243), запишем значение корней характеристического уравнения (2.221), как функции одного параметра a1(0) :
1) действительные корни характеристического уравнения:
|
|
|
a |
|
|
|
a2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
||||||
|
|
|
a K(0) |
|
|
|
|
|
|
||||||||||||||||
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|||||||||||
1,2(a1) |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
, |
D > 0; |
(2.245) |
|||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
2) кратные корни характеристического уравнения: |
|
||||||||||||||||||||||||
|
1 |
(a ) |
2 |
|
|
a1 |
, |
D = 0; |
(2.246) |
||||||||||||||||
|
|
|
|||||||||||||||||||||||
|
1 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3) комплексно-сопряженные корни |
характеристического урав- |
||||||||||||||||||||||||
нения: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
a2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
1 |
|
|
1 |
|
|
a K(0) |
|
|
|
|
|
|
|||||||||||
1,2(a1) |
|
|
|
|
|
|
|
|
|
1 |
|
|
, |
D < 0; |
|
||||||||||
|
a1 |
|
|
|
2 |
|
|
|
|
2 |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
(a ) |
|
; |
|
(a ) |
|
|
|
|
|
|
a2 . |
(2.247) |
|||||||||||||
1 |
|
2 |
|
|
|
1 |
|
|
|
|
a K(0) |
1 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
198
Подставляя (2.245) – (2.247) в формулы расчета корреляционных функций (2.227), (2.230), (2.233) при t tf и принимая во
внимание (2.244), для различных типов корней характеристическо-
го уравнения получим: |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
1) |
для действительных корней характеристического уравнения: |
|||||||||||||||||||||
|
K(tf |
) K(0) |
[ 2(a1)exp ( 1(a1)t1) 1(a1)exp ( 2(a1)t1)] |
0 ; |
||||||||||||||||||
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
( 2(a1) 1(a1)) |
|
|
|
|
|
|
(2.248) |
||||||
2) |
для кратных корней характеристического уравнения: |
|||||||||||||||||||||
|
||||||||||||||||||||||
|
|
|
|
K(tf ) K(0)exp ( (a1)t f |
)(1 (a1)tf |
) 0; |
(2.249) |
|||||||||||||||
3) |
для |
комплексно-сопряженных |
корней |
характеристического |
||||||||||||||||||
уравнения: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
K(t |
|
) K(0)e |
(a )t |
|
|
cos( (a )t |
|
) |
(a ) |
sin ( (a )t |
|
) |
|
0. |
(2.250) |
|||||||
f |
1 |
f |
|
f |
|
1 |
f |
|
||||||||||||||
|
|
|
|
|
|
|
1 |
|
(a1) |
|
1 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Разрешая уравнения (2.248) – (2.250) относительно a1(0) (a0(0) определяется по формуле (2.243)), получим значения a1(0), a0(0),
которые могут быть использованы в качестве начальных приближений.
2.6.3.2. Алгоритм решения задачи методом покоординатного спуска
Как было отмечено в п. 2.6.3.1, метод Ньютона – Гаусса оказывается чувствителен к заданию начальных приближений. Неудачное задание начальных приближений часто приводит к расхождению итерационного процесса.
Вэтой связи методом, более устойчивым к выбору начальных приближений, является метод покоординатного спуска, подробно рассмотренный в гл. 1.
На рис. 2.17 приведена структурная схема решения задачи определения коэффициентов формирующего фильтра с использованием этого метода.
Вкачестве метода одномерной оптимизации при нахождении точки экстремума по каждой координате используется метод «золотого сечения», также рассмотренный в гл. 1.
199
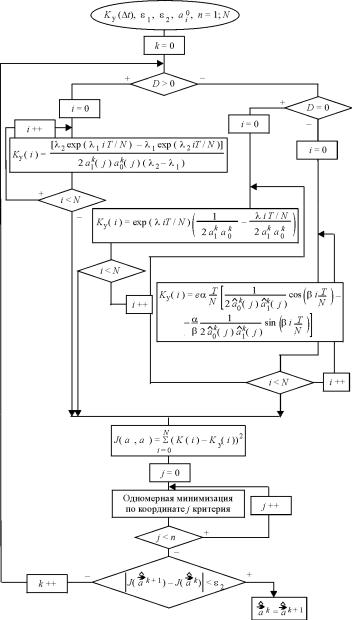
Рис. 2.17. Блок-схема алгоритма метода покоординатного спуска (один цикл)
200
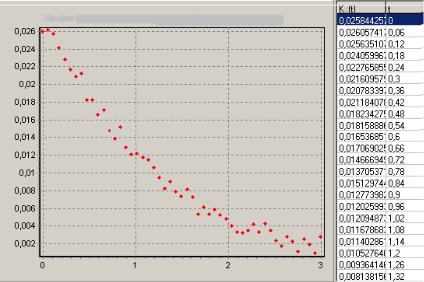
2.6.4. Пример расчета коэффициентов формирующего фильтра
В качестве примера рассмотрим расчет коэффициентов формирующего фильтра, выходом которого является случайный процесс с корреляционной функцией близкой к корреляционной функции, изображенной на рис. 2.18.
Рис. 2.18. Вид корреляционной функции исходного процесса
Данная задача решалась двумя методами:
-методом Ньютона – Гаусса;
-методом покоординатного спуска.
В процессе решения получены результаты, приведенные в табл. 2.8.
Как видно из результатов расчета, метод Ньютона – Гаусса обеспечивает быструю сходимость алгоритма вблизи точки оптимума (варианты расчетов 1 и 2), тогда как при больших отклонениях начальных приближений (a0(0), a1(0)) от оптимальных наблю-
дается расходимость метода (варианты расчетов 3 и 4).
Метод покоординатного спуска обеспечивает более устойчивую сходимость при различных начальных приближениях (варианты расчетов 5 – 8).
201
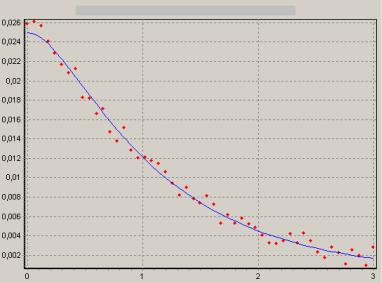
|
|
|
|
|
|
|
|
|
|
Таблица 2.8 |
|
|
Сравнительные характеристики методов оптимизации |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Характеристики |
|
||
Метод |
|
Начальные приближения |
точ- |
итера |
|
a0 |
a1 |
||||
|
|
|
|
|
|
|
ность |
ции |
|
|
|
|
|
|
|
|
|
|
|
||||
Нью- |
1. |
a0(0) 5.45, a1(0) 3.87 |
10e 6 |
2 |
4.999 |
4.0005 |
|||||
тона – |
|
|
|
|
|
|
|
|
|
|
|
2. |
a |
0 |
(0) |
6.00, a |
(0) 6.00 |
10e 6 |
5 |
5.0001 |
3.998 |
||
Гаусса |
|
|
|
1 |
|
|
|
|
|
|
|
|
3. |
a0 |
(0) |
8.00, a1 |
(0) 8.00 |
10e 6 |
Метод расходится |
||||
|
4. |
a0 |
(0) |
15.00, a1(0) 15.00 |
10e 6 |
Метод расходится |
|||||
Поко- |
5. |
a0 |
(0) |
5.45, a1 |
(0) 3.87, |
10e 6 |
5 |
|
5.01 |
3.999 |
|
орди- |
|
|
|
|
|
|
|
|
|
|
|
6. |
a0 |
(0) |
6.00, a1(0) 6.00 |
10e 6 |
9 |
|
5.000 |
4.000 |
|||
натно- |
|
||||||||||
го |
7. |
a0 |
(0) |
8.00, a1 |
(0) 8.00 |
10e 6 |
9 |
|
4.998 |
3.989 |
|
спуска |
|
|
|
|
|
|
|
|
|
||
8. |
a0 |
(0) |
15.00, a1(0) 15.00 |
10e 6 |
11 |
|
5.000 |
4.000 |
|||
На рис. 2.19 изображены графики исходной и модельной корреляционной функций случайных процессов.
Рис. 2.19. Вид корреляционных функций исходного и моделируемого с помощью формирующего фильтра случайных процессов
202
2.7. Оптимальный перехват цели с одним и двумя разворотами
2.7.1. Характеристики вертикального профиля полета истребителя-перехватчика
Общепринято, что для всех типов перехватчиков существует оптимальная траектория вертикального полета на цель [61]. Производя полет по такой траектории, истребитель должен лететь с максимально возможной средней скоростью и минимальным средним расходом топлива.
На рис. 2.12 обозначены участки вертикального профиля полета истребителя. Каждый участок вертикального профиля имеет характеристики: скорость, путь, расход топлива и время полета. Полет перехватчика на некоторых участках (1, 2, 4, 5, 7 и 8) полностью определяется летно-техническими характеристиками (ЛТХ) истребителя. Полет перехватчика на горизонтальных участках (3 и 6) проходит на указанной высоте с постоянным расходом топлива и постоянной скоростью (также указаны в ЛТХ). Поэтому выбор оптимального профиля при решении задачи перехвата цели заключается в определении времени полета на горизонтальных участках. После поражения цели необходимо вернуться на аэродром. Полет на аэродром посадки (привод) проходит с более простым вертикальным профилем (см. рис. 2.12).
Так же, как и при полете на цель, полет перехватчика на аэродром в вертикальной плоскости на участках 10 и 12 полностью определяется из ЛТХ. Полет перехватчика на горизонтальном участке привода проходит на указанной высоте Нпр с заданными в ЛТХ постоянными величинами расхода топлива и скорости. Время полета на этом участке также подлежит определению.
2.7.2. Характеристики горизонтального профиля полета истребителя
При маневре с одним разворотом траектория истребителя состоит из трех участков: прямой линии, участка разворота и прямой линии. Горизонтальный профиль полета истребителя с учетом траектории полета цели представлен на рис. 2.20.
203
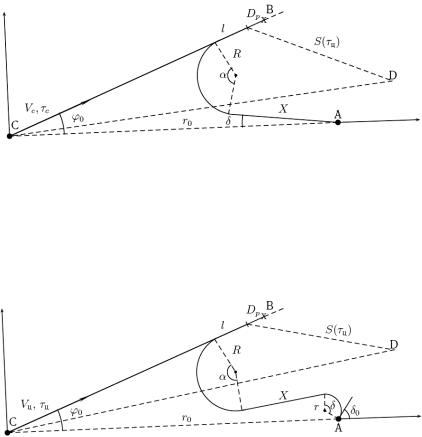
Рис. 2.20. Горизонтальный полет истребителя при маневре с одним разворотом
Маневр с двумя разворотами – это метод, при котором траектория истребителя представляет собой четыре участка: участок разворота, прямую линию, второй участок разворота и прямую линию и позволяет вывести его в заданное положение относительно цели. Горизонтальный профиль полета истребителя с учетом траектории полета цели представлен на рис. 2.21.
Рис. 2.21. Горизонтальный полет истребителя при маневре с двумя разворотами
Истребитель дислоцирован на аэродроме A. В момент обнаружения цель находится в точке C на расстоянии r0 от аэродрома
взлета с курсом 0 . После того, как цель поражена, истребителю
необходимо вернуться на аэродром посадки D.
Прежде чем перейти к рассмотрению поставленных задач и алгоритмов их решения, необходимо указать упрощения, к которым пришлось прибегнуть при построении математической модели.
1. Одним из основных допущений является предположение о прямолинейном и равномерном движении цели. Это допущение
204
сделано потому, что воздушный объект движется к месту своего назначения по кратчайшему пути.
2. Часть земной поверхности, над которой происходит наведение ЛА на цель, считается плоскостью. Поскольку радиус действия авиации и дальность обнаружения целей сравнительно невелики, то полученное решение будет незначительно отличаться от решения с учетом истинной формы земной поверхности. Данное допущение позволяет существенно упростить математические соотношения, описывающие задачу перехвата.
Вероятным вариантом действия противника является массированный налет воздушных объектов противника (целей), действующих по различным направлениям. Возникает задача оценки параметров боевого воздействия истребительной авиации при возможном использовании противником определенного варианта налета.
Исходными данными задачи являются: высота цели, скорость цели, курс цели, точка обнаружения цели, аэродромы взлета и посадки, тип истребителя-перехватчика, тип подвески.
Критерием качества данной задачи можно рассматривать минимум времени полета цели, т.е. минимальное углубление цели
tц min . |
(2.251) |
В задачах перехвата воздушной цели истребителем обычно рассматривают три вида ограничений: баланс времен, баланс путей и баланс топлива. Рассмотрим способ формирования таких ограничений в данной задаче.
1. Баланс времен формируется на основе того, что время движения цели tц и время полета истребителя совпадают:
tкр tN tпас tS |
Dр |
tц , |
(2.252) |
|
Vла V |
||||
|
|
|
где tкр , tN – время полета истребителя на крейсерском и балансном участках вертикального профиля соответственно; tпас – время ожидания на аэродроме; tS – суммарное время движения на участках: регламентное время, первый набор, разгон, второй набор, снижение, конечный участок; Dр – расстояние полета ракеты; V –
превышение скорости ракеты над скоростью истребителя Vла в момент конца наведения.
205
2. Баланс путей учитывает необходимый для уничтожения цели путь перехватчика и ракеты
Vкрtкр VNtN Rd X SS l ( 0 )R , |
(2.253) |
где X – длина первого прямолинейного участка; Vкр , VN – скоро-
сти истребителя соответственно на крейсерском и балансном участках полета; данные величины задаются в ЛТХ; – начальный угол полета ЛА; l – длина второго прямолинейного участка; R – радиус разворота; 0 – курс цели; SS – суммарный путь при дви-
жении на участках: первый набор, разгон, второй набор, снижение, конечный участок.
3. Баланс топлива истребителя
Cкрtкр CNtN qпрS(tц) Gост qпрl G, |
(2.254) |
где Cкр, CN — секундные расходы топлива на крейсерском и балансном участках полета; Gост – неизрасходованный остаток топлива; S(tц ) – путь, который необходимо пройти истребителю до
аэродрома посадки.
Необходимо также ввести дополнительные ограничения. 1. Проекция пути на горизонтальную ось
Vцtц cos 0 X cos Rsin r0 Rsin 0 (l Dp )cos 0 , (2.255) 2. Проекция пути на вертикальную ось
Vцtц sin 0 Xsin Rcos Rcos 0 (l Dp)sin 0, (2.256)
В (2.252) – (2.256) tкр , tN , tпас , tц , , X, Gост являются неиз-
вестными величинами, остальные величины являются постоянными и задаются при помощи ЛТХ и ТТХ истребителя.
Для неизвестных величин необходимо выполнение условия неотрицательности
tкр 0, tN 0, tпас 0, tц 0, 0, X 0, Gост 0. |
(2.257) |
Условия (2.251) – (2.257) представляют собой задачу нелинейного программирования.
206

2.7.3. Решение задачи перехвата с одним разворотом методом штрафных функций
Запишем критерий с помощью метода штрафных функций
(см. п.1.4.1)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D |
|
|
2 |
|
|
|
||||
|
F t m t |
|
|
|
t |
|
t |
|
t |
|
|
|
|
|
|
p |
|
|
t |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
DV |
|
|
||||||||||||||||||
|
|
|
ц |
1 кр |
|
|
N |
|
пас |
|
|
S |
V |
|
ц |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ла |
|
|
|
|
|
|
|
|
|||
m [V t |
кр |
V |
N |
t |
N |
R X S |
S |
l ( |
0 |
)R]2 |
|
|
|||||||||||||||||||
2 |
кр |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
m [C t |
кр |
C |
t |
N |
q |
пр |
S(t |
ц |
) G |
|
q l G]2 |
|
|
||||||||||||||||||
3 |
кр |
|
|
|
N |
|
|
|
|
|
|
|
|
|
|
ост |
|
|
пр |
|
|
|
|
||||||||
m [V t cos Xcos Rsin r Rsin (l D )cos ]2 |
|
||||||||||||||||||||||||||||||
4 ц ц |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
0 |
|
|
|
p |
0 |
|
||
m5[Vцtцsin 0 Xsin Rcos Rcos 0 (l Dp)sin 0]2
m6(tкр2 [1 sgntкр] tN2[1 sgntN] tпас2 [1 sgntпас] tц2[1 sgntц]
2[1 sgn ] Gсот2 [1 sgnGост ]
X |
2[1 sgnX]) min, m 0, |
i 1,...,6. |
(2.258) |
|
i |
|
|
Применим метод покоординатного спуска для решения задачи поиска безусловного минимума функции. Будем использовать метод золотого сечения (см. п.1.2.3) для нахождения оптимального значения по каждой координате. Выберем интервалы поиска минимума по каждой координате таким образом, чтобы выполнялись ограничения, причем интервалы поиска необходимо выбирать достаточно малыми. При таком выборе интервалов поиска необходимость их учета в целевой функции исчезает, поэтому целевую функцию можно переписать в виде
F tц m1 tкр tN tпас tS VлаDp V tц 2
m2[Vкрtкр VNtN R X SS l ( 0)R]2
m3[Cкрtкр CNtN qпрS(tц) Gост qпрl G]2
207
m [V t |
cos Xcos Rsin r |
Rsin (l D )cos ]2 |
||||
4 ц ц |
0 |
|
0 |
0 |
p |
0 |
|
m5[Vцtц sin 0 X sin Rcos Rcos 0 |
|
||||
|
(l D )sin ]2 |
min, |
m 0, i 1,...,5. |
(2.259) |
||
|
p |
0 |
|
i |
|
|
Поскольку каждая из переменных tпас, Gост |
встречается только |
|||||
в одном ограничении, то будем использовать эти равенства для их определения:
|
Dp |
|
|
|
tпас tц tкр tN tS |
|
|
; |
(2.260) |
|
||||
|
Vла V |
|
|
|
Gост G [Cкрtкр CNtN qпрS(tц ) qпрl]. |
(2.261) |
|||
Тогда перепишем целевую функцию
Ftц m{[Vкрtкр VNtN R X SS l ( 0)R]2
[Vцtц cos 0 X cos Rsin r0 Rsin 0 (l Dp)cos 0]2
[Vцtц sin 0 Xsin Rcos Rcos 0
(l D )sin ]2 |
} min, m 0. |
(2.262) |
|
p |
0 |
|
|
Исследования показали, что наилучшие результаты в данной задаче получаются при mi m 10 , i 1,5.
Как правило, путь, необходимый для перехода с крейсерского участка на балансный, достаточно велик и превосходит величину l. В этом случае этот переход необходимо осуществлять до выполнения разворота и проходить этот разворот на скорости, соответствующей балансному участку. В зависимости от скорости полета при выполнении разворота (она является постоянной на всем протяжении участка разворота) радиус разворота может принимать различные фиксированные значения. На балансный участок надо переходить на прямолинейном участке до разворота. Математически это ограничение можно записать в виде
208
tN |
R( 0 |
) l |
. |
(2.263) |
VN |
|
|||
|
|
|
|
С учетом данного ограничения решение задачи становится физически реализуемым с точки зрения значений величины tN .
2.7.4.Перехват цели с двумя разворотами
Взадаче перехвата с одним разворотом предполагается, что угол, под которым происходит вылет ЛА с аэродрома взлета, меняется и определяется в результате решения задачи. На практике такое встречается редко. Обычно взлетно-посадочная полоса строго ориентирована в пространстве. Это означает, что угол вылета не может изменяться. В связи с этим возникает задача перехвата с двумя разворотами. Она строится аналогично задаче с одним разворотом, но перед первым прямолинейным участком добавляется разворот.
Исходными данными задачи являются: высота цели, скорость цели, курс цели, точка обнаружения цели, аэродромы взлета и посадки, тип истребителя-перехватчика, тип подвески.
Критерием качества данной задачи также можно рассматривать минимум времени полета цели, т.е. минимальное углубление цели
tц min . |
(2.264) |
В задачах по перехвату воздушной цели истребителем обычно рассматривают три вида ограничений: баланс времен, баланс путей и баланс топлива. Рассмотрим способ формирования таких ограничений в данной задаче.
Баланс времен и топлива аналогичен предыдущей задаче. Баланс путей учитывает необходимый для уничтожения цели
путь перехватчика и ракеты:
Vкрtкр VNtN (R r) X SS l ( 0 0 )R, |
(2.265) |
где r, R – радиусы 1-го и 2-го разворотов соответственно.
Проекция пути на горизонтальную ось отличается от предыдущей:
209
Vцtц cos 0 X cos( 0) (R r)sin( 0)
r0 rsin 0 Rsin 0 (l Dp )cos 0 . |
(2.266) |
Проекция пути на вертикальную ось |
|
Vцtц sin 0 Xsin( 0) (r R)cos( 0) |
|
rcos 0 Rcos 0 (l Dp )sin 0 . |
(2.267) |
Неизвестными величинами являются tкр , tN , tпас , |
tц , , X, |
Gост , остальные величины являются постоянными и задаются при
помощи ЛТХ и ТТХ истребителя.
Для неизвестных величин необходимо выполнение условия неотрицательности
tкр 0, tN 0, tпас 0, tц 0, 0, X 0, Gост 0. |
(2.268) |
2.7.5. Решение задачи перехвата с двумя разворотами методом штрафных функций
Запишем критерий с помощью метода штрафных функций
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D |
|
|
|
|
2 |
|
F t |
ц |
m t |
|
|
t |
N |
t |
пас |
t |
S |
|
|
p |
t |
ц |
|
|||||||||||
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
1 кр |
|
|
|
|
|
|
Vла V |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
m |
[V |
|
t |
кр |
V |
N |
t |
N |
R X S |
S |
l ( |
0 |
)R]2 |
||||||||||||||
2 |
|
кр |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
m3[Cкр |
tкр |
CN |
tN qпрS(tц ) Gост qпр l G]2 |
||||||||||||||||||||||||
m 4[Vц |
tц cos 0 X cos ( 0 ) (r R)sin ( 0 ) r0 |
||||||||||||||||||||||||||
|
|
rsin 0 |
|
Rsin 0 |
(l Dp )cos 0 ]2 |
|
|
|
|||||||||||||||||||
m 5 [Vц |
tц sin 0 |
|
X sin ( 0 ) (r R)cos ( 0 ) |
||||||||||||||||||||||||
|
|
rcos 0 |
Rcos 0 |
|
(l Dp )sin 0 ]2 |
|
|
|
|||||||||||||||||||
m6 {tкр2 [1 sgn tкр ] tN2 [1 sgn tN ] tпас2 [1 sgn tпас ]
tц2 [1 sgntц] 2 [1 sgn ] Gост2 [1 sgnGост] X2 [1 sgn X]} min, mi 0, i 1,...,6.
(2.269)
210
Применим метод покоординатного спуска для решения задачи поиска безусловного минимума целевой функции. Будем использовать метод “золотого сечения” для нахождения оптимального значения по каждой координате. Далее в этой задаче проводятся преобразования, подобные приведенным в п. 2.7.4. Исследования показали, что наилучшие результаты в данной задаче получаются при
mi m 10 , i 1,5.
В большинстве случаев путь, необходимый для перехода с крейсерского участка на балансный, достаточно велик и превосходит величину l. В таком случае этот переход необходимо осуществлять до выполнения разворота и проходить этот разворот на скорости, соответствующей балансному участку. В зависимости от скорости полета при выполнении разворота (она является постоянной на всем протяжении участка разворота) радиус разворота может принимать различные фиксированные значения. При необходимости на балансный участок надо переходить на прямолинейном участке до разворота. Математически это ограничение можно записать в виде
tN |
|
R( 0 |
) l |
. |
(2.270) |
VN |
|
||||
|
|
|
|
|
С учетом данного ограничения решение задачи становится физически реализуемым с точки зрения значений величины tN .
Для расчетов были выбраны следующие исходные данные:
r |
800 , |
|
0 |
20o , |
V |
ц |
250, |
t |
S |
300, |
S |
S |
160, |
V |
кр |
250 , |
||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
VN 400, |
V 300 м/с, |
Cкр 1.5 |
кг/с, |
|
CN 6 кг/с, |
||||||||||||
|
Cдеж 1.7 |
|
кг/с, |
qпр 5 кг/с, |
|
Hат 11 км, |
Dp 30 км, |
|||||||||||
|
Rв 50 км, |
|
G 13000 кг, |
r 10 км, |
R 10 км, |
l 10 км, |
||||||||||||
0 30o .
Результаты приведены в табл. 2.9–2.19. Величина характеризует точность нахождения экстремума методом золотого сечения для каждой координаты, а величина – относительную точность решения.
211
Таблица 2.9
Анализ результатов в зависимости от скорости полета цели
|
|
|
10 1 , |
10 2 |
|
|
|
||||||
№ |
Параметр |
ц, с |
кр, с |
|
N, с |
|
пас, с |
, |
Gост, кг |
X, км |
Число |
||
|
|
итераций |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
Vц = 200 м/с |
2114.25 |
1632.53 |
0.01 |
|
|
0.00 |
14.29 |
8362.00 |
453.00 |
13 |
||
2 |
Vц = 250 м/с |
1926.09 |
1444.09 |
0.01 |
|
|
0.03 |
18.95 |
8860.64 |
406.72 |
10 |
||
3 |
Vц = 300 м/с |
1774.07 |
1292.31 |
0.00 |
|
|
0.03 |
23.90 |
9257.50 |
369.56 |
13 |
||
4 |
Vц = 350 м/с |
1516.89 |
742.94 |
234.44 |
|
0.03 |
18.22 |
8670.82 |
355.46 |
12 |
|||
5 |
Vц = 400 м/с |
1412.49 |
638.50 |
234.46 |
|
0.06 |
21.88 |
8929.10 |
331.28 |
13 |
|||
6 |
Vц = 450 м/с |
1323.79 |
549.81 |
234.43 |
|
0.07 |
25.67 |
9143.75 |
311.08 |
15 |
|||
7 |
Vц = 500 м/с |
1198.91 |
334.35 |
304.26 |
|
0.05 |
22.94 |
9057.17 |
299.77 |
15 |
|||
8 |
Vц = 550 м/с |
1132.37 |
267.82 |
304.24 |
|
0.05 |
26.15 |
9210.42 |
285.36 |
17 |
|||
9 |
Vц = 600 м/с |
1076.05 |
219.72 |
296.03 |
|
0.04 |
29.62 |
9376.83 |
272.48 |
20 |
|||
10 |
Vц = 650 м/с |
1024.81 |
168.52 |
295.99 |
|
0.04 |
33.05 |
9487.77 |
262.06 |
23 |
|||
11 |
Vц = 700 м/с |
973.13 |
55.52 |
329.53 |
|
0.03 |
32.12 |
9476.69 |
244.25 |
24 |
|||
12 |
Vц = 750 м/с |
935.65 |
36.08 |
311.50 |
|
0.03 |
36.10 |
9636.11 |
235.65 |
29 |
|||
13 |
Vц = 800 м/с |
902.49 |
18.96 |
295.47 |
|
0.03 |
40.34 |
9772.61 |
228.68 |
37 |
|||
14 |
Vц = 850 м/с |
873.82 |
6.45 |
279.31 |
|
0.03 |
45.02 |
9895.66 |
223.19 |
52 |
|||
15 |
Vц = 900 м/с |
|
|
|
Задача не имеет решения |
|
|
||||||
16 |
Vц = 950 м/с |
|
|
|
Задача не имеет решения |
|
|
||||||
17 |
Vц = 1000 м/с |
|
|
|
Задача не имеет решения |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 2.10 |
|
|
|
Анализ результатов в зависимости |
|
|
|||||||||
|
|
от взаимного расстояния цель-истребитель |
|
|
|||||||||
|
|
|
10 1 , |
10 2 |
|
|
|
||||||
№ |
Параметр |
ц, с |
кр, с |
|
N, с |
|
пас, с |
|
, |
Gост, кг |
X, км |
Число |
|
|
|
|
итераций |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
r0 = 100 км |
|
|
|
Задача не имеет решения |
|
|
||||||
2 |
r0 = 200 км |
649.68 |
167.95 |
|
0.00 |
|
0.01 |
|
15.17 |
9449.29 |
86.95 |
10 |
|
3 |
r0 = 300 км |
862.23 |
380.46 |
|
0.01 |
|
0.04 |
|
16.98 |
9369.40 |
140.41 |
9 |
|
4 |
r0 = 400 км |
1074.93 |
593.17 |
|
0.01 |
|
0.03 |
|
17.80 |
9284.54 |
193.73 |
9 |
|
5 |
r0 = 500 км |
1287.70 |
805.95 |
|
0.00 |
|
0.02 |
|
18.27 |
9193.41 |
247.00 |
10 |
|
6 |
r0 = 600 км |
1500.48 |
1018.73 |
|
0.01 |
|
0.02 |
|
18.58 |
9094.21 |
300.26 |
10 |
|
7 |
r0 = 700 км |
1713.28 |
1231.53 |
|
0.00 |
|
0.02 |
|
18.79 |
8984.46 |
353.49 |
10 |
|
8 |
r0 = 800 км |
1926.09 |
1444.33 |
|
0.01 |
|
0.03 |
|
18.95 |
8860.64 |
406.72 |
10 |
|
9 |
r0 = 900 км |
2138.89 |
1657.15 |
|
0.01 |
|
0.02 |
|
19.07 |
8718.05 |
459.95 |
10 |
|
10 |
r0 = 1000 км |
2351.72 |
1869.96 |
|
0.00 |
|
0.03 |
|
19.17 |
8550.48 |
513.17 |
10 |
|
11 |
r0 = 1100 км |
2564.54 |
2082.78 |
|
0.00 |
|
0.04 |
|
19.24 |
8350.15 |
566.39 |
10 |
|
12 |
r0 = 1200 км |
2777.36 |
2295.61 |
|
0.01 |
|
0.02 |
|
19.31 |
8108.68 |
619.61 |
10 |
|
13 |
r0 = 1300 км |
2990.19 |
2508.43 |
|
0.01 |
|
0.03 |
|
19.36 |
7819.08 |
672.82 |
10 |
|
14 |
r0 = 1400 км |
3203.01 |
2721.25 |
|
0.00 |
|
0.03 |
|
19.41 |
7478.25 |
726.04 |
10 |
|
15 |
r0 = 1500 км |
3415.84 |
2934.08 |
|
0.00 |
|
0.03 |
|
19.45 |
7088.45 |
779.26 |
10 |
|
16 |
r0 = 1600 км |
3628.67 |
3146.91 |
|
0.00 |
|
0.03 |
|
19.48 |
6656.24 |
832.47 |
10 |
|
17 |
r0 = 1700 км |
3841.50 |
3359.73 |
|
0.00 |
|
0.05 |
|
19.52 |
6190.00 |
885.68 |
10 |
|
18 |
r0 = 1800 км |
4054.33 |
3572.58 |
|
0.01 |
|
0.02 |
|
19.54 |
5697.55 |
938.89 |
11 |
|
19 |
r0 = 1900 км |
4267.18 |
3785.42 |
|
0.01 |
|
0.03 |
|
19.57 |
5185.48 |
992.11 |
11 |
|
20 |
r0 = 2000 км |
4480.01 |
3998.26 |
|
0.01 |
|
0.02 |
|
19.59 |
4658.72 |
1045.32 |
11 |
|
212
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 2.11 |
|
|
|
Анализ результатов в зависимости |
|
|
|||||||||
|
|
|
от скорости полета цели |
|
|
|
|||||||
|
|
|
10 6 , |
10 8 |
|
|
|
||||||
№ |
Параметр |
ц, с |
кр, с |
|
N, с |
|
пас, с |
, |
Gост, кг |
X, км |
Число |
||
|
|
итераций |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
Vц = 200 м/с |
2114.25 |
1632.52 |
0.00 |
|
|
0.00 |
14.29 |
8362.03 |
453.00 |
19 |
||
2 |
Vц = 250 м/с |
1926.09 |
1444.36 |
0.00 |
|
|
0.00 |
18.95 |
8860.63 |
406.73 |
22 |
||
3 |
Vц = 300 м/с |
1774.07 |
1292.35 |
0.00 |
|
|
0.00 |
23.90 |
9257.48 |
369.57 |
27 |
||
4 |
Vц = 350 м/с |
1516.89 |
742.98 |
234.44 |
|
0.00 |
18.22 |
8670.79 |
355.47 |
25 |
|||
5 |
Vц = 400 м/с |
1412.49 |
638.63 |
234.44 |
|
0.00 |
21.88 |
8929.10 |
331.28 |
30 |
|||
6 |
Vц = 450 м/с |
1323.79 |
549.94 |
234.44 |
|
0.00 |
25.67 |
9143.59 |
311.09 |
36 |
|||
7 |
Vц = 500 м/с |
1198.91 |
334.46 |
304.25 |
|
0.00 |
22.95 |
9057.14 |
299.77 |
34 |
|||
8 |
Vц = 550 м/с |
1132.37 |
267.91 |
304.25 |
|
0.00 |
26.15 |
9210.28 |
285.37 |
40 |
|||
9 |
Vц = 600 м/с |
1076.05 |
219.85 |
296.01 |
|
0.00 |
29.63 |
9376.86 |
272.48 |
47 |
|||
10 |
Vц = 650 м/с |
1024.81 |
168.61 |
296.01 |
|
0.00 |
33.07 |
9487.58 |
262.07 |
55 |
|||
11 |
Vц = 700 м/с |
973.13 |
55.67 |
329.50 |
|
0.00 |
32.14 |
9476.71 |
244.25 |
57 |
|||
12 |
Vц = 750 м/с |
935.65 |
36.21 |
311.50 |
|
0.00 |
36.12 |
9635.98 |
235.66 |
70 |
|||
13 |
Vц = 800 м/с |
902.49 |
19.09 |
295.48 |
|
0.00 |
40.37 |
9772.40 |
228.69 |
92 |
|||
14 |
Vц = 850 м/с |
873.82 |
6.59 |
279.37 |
|
0.00 |
45.06 |
9895.13 |
223.23 |
125 |
|||
15 |
Vц = 900 м/с |
|
|
|
Задача не имеет решения |
|
|
||||||
16 |
Vц = 950 м/с |
|
|
|
Задача не имеет решения |
|
|
||||||
17 |
Vц = 1000 м/с |
|
|
|
Задача не имеет решения |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 2.12 |
|
|
|
Анализ результатов в зависимости |
|
|
|||||||||
|
|
от взаимного расстояния цель-истребитель |
|
|
|||||||||
|
|
|
10 6 , |
10 8 |
|
|
|
||||||
№ |
Параметр |
ц, с |
кр, с |
|
N, с |
|
пас, с |
|
, |
Gост, кг |
X, км |
Число |
|
|
|
|
итераций |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
r0 = 100 км |
|
|
|
Задача не имеет решения |
|
|
||||||
2 |
r0 = 200 км |
649.68 |
167.95 |
|
0.00 |
|
0.00 |
|
15.17 |
9449.30 |
86.96 |
19 |
|
3 |
r0 = 300 км |
862.23 |
380.50 |
|
0.00 |
|
0.00 |
|
16.98 |
9369.37 |
140.41 |
19 |
|
4 |
r0 = 400 км |
1074.93 |
593.20 |
|
0.00 |
|
0.00 |
|
17.80 |
9284.51 |
193.74 |
19 |
|
5 |
r0 = 500 км |
1287.69 |
805.96 |
|
0.00 |
|
0.00 |
|
18.27 |
9193.40 |
247.01 |
20 |
|
6 |
r0 = 600 км |
1500.47 |
1018.75 |
|
0.00 |
|
0.00 |
|
18.58 |
9094.21 |
300.26 |
20 |
|
7 |
r0 = 700 км |
1713.28 |
1231.55 |
|
0.00 |
|
0.00 |
|
18.79 |
8984.44 |
353.50 |
20 |
|
8 |
r0 = 800 км |
1926.08 |
1444.36 |
|
0.00 |
|
0.00 |
|
18.95 |
8860.63 |
406.73 |
22 |
|
9 |
r0 = 900 км |
2138.90 |
1657.18 |
|
0.00 |
|
0.00 |
|
19.07 |
8718.04 |
459.95 |
20 |
|
10 |
r0 = 1000 км |
2351.72 |
1870.00 |
|
0.00 |
|
0.00 |
|
19.17 |
8550.45 |
513.18 |
22 |
|
11 |
r0 = 1100 км |
2564.54 |
2082.82 |
|
0.00 |
|
0.00 |
|
19.24 |
8350.12 |
566.40 |
23 |
|
12 |
r0 = 1200 км |
2777.37 |
2295.64 |
|
0.00 |
|
0.00 |
|
19.31 |
8108.66 |
619.61 |
24 |
|
13 |
r0 = 1300 км |
2990.19 |
2508.47 |
|
0.00 |
|
0.00 |
|
19.36 |
7819.05 |
672.83 |
22 |
|
14 |
r0 = 1400 км |
3203.02 |
2721.30 |
|
0.00 |
|
0.00 |
|
19.41 |
7478.21 |
726.05 |
20 |
|
15 |
r0 = 1500 км |
3415.85 |
2934.13 |
|
0.00 |
|
0.00 |
|
19.45 |
7088.39 |
779.26 |
20 |
|
16 |
r0 = 1600 км |
3628.68 |
3146.96 |
|
0.00 |
|
0.00 |
|
19.48 |
6656.19 |
832.47 |
24 |
|
17 |
r0 = 1700 км |
3841.51 |
3359.79 |
|
0.00 |
|
0.00 |
|
19.52 |
6189.93 |
885.69 |
26 |
|
18 |
r0 = 1800 км |
4054.34 |
3572.62 |
|
0.00 |
|
0.00 |
|
19.54 |
5697.52 |
938.90 |
20 |
|
19 |
r0 = 1900 км |
4267.17 |
3785.45 |
|
0.00 |
|
0.00 |
|
19.57 |
5185.47 |
992.11 |
23 |
|
20 |
r0 = 2000 км |
4480.01 |
3998.28 |
|
0.00 |
|
0.00 |
|
19.59 |
4658.72 |
1045.32 |
23 |
|
213
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 2.13 |
||
|
|
|
|
Анализ результатов в зависимости |
|
|
|
||||||||||
|
|
|
|
|
от курса полета цели |
|
|
|
|
|
|
||||||
|
|
|
|
|
10 6 , |
10 8 |
|
|
|
|
|
|
|||||
|
№ |
Параметр |
|
ц, с |
кр, с |
N, с |
|
пас, с |
|
, |
|
Gост, кг |
|
X, км |
|
Число |
|
|
|
|
|
|
|
|
итераций |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
0 = 5 |
1843.34 |
1361.61 |
0.00 |
|
0.00 |
|
2.52 |
8910.71 |
|
380.50 |
8 |
||||
|
2 |
0 = 10 |
1856.33 |
1374.61 |
0.00 |
|
0.00 |
|
8.03 |
8903.02 |
|
385.59 |
11 |
||||
|
3 |
0 = 15 |
1883.51 |
1401.79 |
0.00 |
|
0.00 |
|
13.51 |
8886.72 |
|
394.23 |
15 |
||||
|
4 |
0 = 20 |
1926.08 |
1444.36 |
0.00 |
|
0.00 |
|
18.95 |
8860.63 |
|
406.73 |
22 |
||||
|
5 |
0 = 25 |
1985.97 |
1504.24 |
0.00 |
|
0.00 |
|
24.35 |
8822.64 |
|
423.56 |
30 |
||||
|
6 |
0 = 30 |
2066.00 |
1584.27 |
0.00 |
|
0.00 |
|
29.70 |
8769.36 |
|
445.47 |
44 |
||||
|
7 |
0 = 35 |
2170.06 |
1688.34 |
0.00 |
|
0.00 |
|
34.99 |
8695.24 |
|
473.47 |
73 |
||||
|
8 |
0 = 40 |
2302.15 |
1820.43 |
0.00 |
|
0.00 |
|
40.16 |
8592.11 |
|
508.85 |
167 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 2.14 |
||
|
|
|
|
Анализ результатов в зависимости |
|
|
|
||||||||||
|
|
|
|
|
от скорости полета цели |
|
|
|
|
|
|
||||||
|
|
|
|
|
10 1 , |
10 2 |
|
|
|
|
|
|
|||||
|
№ |
Параметр |
|
ц, с |
кр, с |
N, с |
|
пас, с |
, |
|
Gост, кг |
X, км |
|
Число |
|||
|
|
|
|
|
итераций |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
Vц = 200 м/с |
|
2127.28 |
1645.55 |
0.01 |
|
|
0.00 |
137.74 |
|
8352.47 |
|
443.44 |
|
139 |
|
|
2 |
Vц = 250 м/с |
|
1935.19 |
1453.41 |
0.01 |
|
|
0.05 |
133.23 |
|
8854.99 |
|
396.95 |
|
9 |
|
|
3 |
Vц = 300 м/с |
|
1779.77 |
1298.01 |
0.00 |
|
|
0.03 |
128.44 |
|
9254.29 |
|
359.74 |
|
12 |
|
|
4 |
Vц = 350 м/с |
|
1481.85 |
707.91 |
234.44 |
|
0.03 |
135.67 |
|
8684.26 |
|
355.76 |
|
11 |
||
|
5 |
Vц = 400 м/с |
|
1377.31 |
603.34 |
234.45 |
|
0.04 |
132.52 |
|
8941.21 |
|
331.82 |
|
12 |
||
|
6 |
Vц = 450 м/с |
|
1288.78 |
517.31 |
231.96 |
|
0.03 |
129.26 |
|
9166.84 |
|
311.57 |
|
14 |
||
|
7 |
Vц = 500 м/с |
|
1201.19 |
557.68 |
83.22 |
|
|
0.03 |
130.07 |
|
10051.20 |
288.74 |
|
14 |
||
|
8 |
Vц = 550 м/с |
|
1133.37 |
490.50 |
82.58 |
|
|
0.02 |
127.00 |
|
10207.53 |
274.36 |
|
16 |
||
|
9 |
Vц = 600 м/с |
|
1072.58 |
424.45 |
87.85 |
|
|
0.02 |
123.98 |
|
10315.04 |
262.59 |
|
18 |
||
|
10 |
Vц = 650 м/с |
|
1018.85 |
365.36 |
93.20 |
|
|
0.02 |
120.92 |
|
10403.32 |
252.64 |
|
20 |
||
|
11 |
Vц = 700 м/с |
|
956.55 |
264.00 |
104.50 |
|
0.01 |
123.55 |
|
10498.55 |
237.78 |
|
19 |
|||
|
12 |
Vц = 750 м/с |
|
912.75 |
214.28 |
110.42 |
|
0.02 |
120.84 |
|
10557.33 |
230.56 |
|
21 |
|||
|
13 |
Vц = 800 м/с |
|
873.31 |
168.87 |
116.39 |
|
0.02 |
118.11 |
|
10604.76 |
224.47 |
|
23 |
|||
|
14 |
Vц = 850 м/с |
|
837.69 |
127.20 |
122.44 |
|
0.02 |
115.33 |
|
10642.16 |
219.36 |
|
27 |
|||
|
15 |
Vц = 900 м/с |
|
805.37 |
88.78 |
128.54 |
|
0.02 |
112.54 |
|
10670.91 |
215.14 |
|
30 |
|||
|
16 |
Vц = 950 м/с |
|
776.01 |
53.22 |
134.74 |
|
0.01 |
109.69 |
|
10691.73 |
211.71 |
|
34 |
|||
|
17 |
Vц = 1000 м/с |
|
749.27 |
20.17 |
141.05 |
|
0.01 |
106.80 |
|
10705.30 |
209.02 |
|
39 |
|||
214
|
|
|
|
|
|
|
|
|
|
|
Таблица 2.15 |
|
|
|
|
Анализ результатов в зависимости |
|
|
|||||||
|
|
|
от взаимного расстояния цель-истребитель |
|
|
|||||||
|
|
|
|
10 1 , |
10 2 |
|
|
|
|
|||
№ |
Параметр |
ц, с |
кр, с |
N, с |
|
пас, с |
, |
Gост, кг |
|
X, км |
Число |
|
|
|
итераций |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
r0 = 100 км |
|
|
Задача не имеет решения |
|
|
||||||
2 |
r0 = 200 км |
663.71 |
181.97 |
0.00 |
|
0.02 |
146.12 |
9444.15 |
|
74.55 |
8 |
|
3 |
r0 = 300 км |
873.84 |
392.08 |
0.01 |
|
0.03 |
139.64 |
9364.89 |
|
129.36 |
8 |
|
4 |
r0 = 400 км |
1085.48 |
603.73 |
0.01 |
|
0.02 |
136.90 |
9280.16 |
|
183.23 |
9 |
|
5 |
r0 = 500 км |
1297.64 |
815.90 |
0.00 |
|
0.01 |
135.37 |
9188.96 |
|
236.81 |
9 |
|
6 |
r0 = 600 км |
1510.05 |
1028.28 |
0.01 |
|
0.04 |
134.40 |
9089.56 |
|
290.25 |
9 |
|
7 |
r0 = 700 км |
1722.58 |
1240.82 |
0.00 |
|
0.03 |
133.73 |
8979.38 |
|
343.62 |
9 |
|
8 |
r0 = 800 км |
1935.19 |
1453.41 |
0.01 |
|
0.05 |
133.23 |
8854.99 |
|
396.95 |
9 |
|
9 |
r0 = 900 км |
2147.87 |
1666.11 |
0.01 |
|
0.03 |
132.86 |
8711.55 |
|
450.25 |
10 |
|
10 |
r0 = 1000 км |
2360.56 |
1878.82 |
0.00 |
|
0.01 |
132.56 |
8542.84 |
|
503.53 |
10 |
|
11 |
r0 = 1100 км |
2573.28 |
2091.53 |
0.00 |
|
0.02 |
132.31 |
8341.08 |
|
556.80 |
10 |
|
12 |
r0 = 1200 км |
2786.02 |
2304.28 |
0.01 |
|
0.01 |
132.11 |
8097.86 |
|
610.05 |
10 |
|
13 |
r0 = 1300 км |
2998.79 |
2517.03 |
0.01 |
|
0.03 |
131.94 |
7806.30 |
|
663.30 |
10 |
|
14 |
r0 = 1400 км |
3211.56 |
2729.81 |
0.00 |
|
0.02 |
131.80 |
7463.50 |
|
716.54 |
10 |
|
15 |
r0 = 1500 км |
3424.34 |
2942.58 |
0.00 |
|
0.03 |
131.68 |
7071.94 |
|
769.78 |
10 |
|
16 |
r0 = 1600 км |
3637.12 |
3155.36 |
0.00 |
|
0.03 |
131.57 |
6638.32 |
|
823.02 |
10 |
|
17 |
r0 = 1700 км |
3849.91 |
3368.16 |
0.00 |
|
0.02 |
131.47 |
6170.95 |
|
876.25 |
10 |
|
18 |
r0 = 1800 км |
4062.71 |
3580.95 |
0.01 |
|
0.03 |
131.39 |
5677.74 |
|
929.48 |
10 |
|
19 |
r0 = 1900 км |
4275.51 |
3793.76 |
0.00 |
|
0.02 |
131.32 |
5165.09 |
|
982.71 |
7 |
|
20 |
r0 = 2000 км |
4488.34 |
4006.61 |
0.01 |
|
0.00 |
131.25 |
4637.82 |
|
1035.93 |
39 |
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 2.16 |
|
|
|
|
Анализ результатов в зависимости |
|
|
|||||||
|
|
|
|
от курса полета цели |
|
|
|
|
||||
|
|
|
|
10 1 , |
10 2 |
|
|
|
|
|||
№ |
Параметр |
|
ц, с |
кр, с |
N, с |
|
пас, с |
, |
Gост, кг |
|
X, км |
Число |
|
|
|
итераций |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
0 = 5 |
|
1858.17 |
1376.43 |
0.00 |
|
0.01 |
150.25 |
8901.92 |
|
370.92 |
33 |
2 |
0 = 10 |
|
1868.89 |
1387.15 |
0.01 |
|
0.01 |
144.54 |
8895.52 |
|
375.93 |
5 |
3 |
0 = 15 |
|
1894.18 |
1412.43 |
0.01 |
|
0.02 |
138.87 |
8880.25 |
|
384.51 |
7 |
4 |
0 = 20 |
|
1935.19 |
1453.41 |
0.01 |
|
0.05 |
133.23 |
8854.99 |
|
396.95 |
9 |
5 |
0 = 25 |
|
1993.82 |
1512.06 |
0.01 |
|
0.02 |
127.64 |
8817.56 |
|
413.72 |
13 |
6 |
0 = 30 |
|
2072.90 |
1591.12 |
0.01 |
|
0.05 |
122.08 |
8764.67 |
|
435.55 |
18 |
7 |
0 = 35 |
|
2176.37 |
1694.56 |
0.00 |
|
0.08 |
116.58 |
8690.66 |
|
463.49 |
27 |
8 |
0 = 40 |
|
2308.62 |
1826.81 |
0.00 |
|
0.09 |
111.19 |
8586.88 |
|
498.87 |
50 |
215
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 2.17 |
|
|
|
|
Анализ результатов в зависимости |
|
|
||||||||||||
|
|
|
|
от скорости полета цели |
|
|
|
|
|||||||||
|
|
|
|
10 6 , |
10 8 |
|
|
|
|
||||||||
№ |
Параметр |
ц, с |
кр, с |
|
N, с |
|
пас, с |
|
, |
Gост, кг |
X, км |
Число |
|||||
|
|
|
итераций |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
Vц = 200 |
м/с |
2127.26 |
1645.53 |
0.00 |
|
|
0.00 |
|
137.74 |
|
8352.50 |
|
443.45 |
142 |
||
2 |
Vц = 250 |
м/с |
1935.18 |
1453.45 |
0.00 |
|
|
0.00 |
|
133.23 |
|
8854.96 |
|
396.95 |
20 |
||
3 |
Vц = 300 |
м/с |
1779.77 |
1298.04 |
0.00 |
|
|
0.00 |
|
128.44 |
|
9254.27 |
|
359.75 |
25 |
||
4 |
Vц = 350 |
м/с |
1481.85 |
707.94 |
234.44 |
|
0.00 |
|
135.67 |
|
8684.21 |
|
355.76 |
22 |
|||
5 |
Vц = 400 |
м/с |
1377.33 |
603.42 |
234.44 |
|
0.00 |
|
132.51 |
|
8941.22 |
|
331.82 |
26 |
|||
6 |
Vц = 450 |
м/с |
1288.80 |
517.36 |
231.96 |
|
0.00 |
|
129.25 |
|
9166.81 |
|
311.58 |
30 |
|||
7 |
Vц = 500 |
м/с |
1201.22 |
557.75 |
83.22 |
|
|
0.00 |
|
130.07 |
|
10051.15 |
288.74 |
31 |
|||
8 |
Vц = 550 |
м/с |
1133.40 |
490.55 |
82.60 |
|
|
0.00 |
|
127.00 |
|
10207.41 |
274.36 |
36 |
|||
9 |
Vц = 600 |
м/с |
1072.62 |
424.50 |
87.87 |
|
|
0.00 |
|
123.98 |
|
10314.91 |
262.59 |
41 |
|||
10 |
Vц = 650 |
м/с |
1018.90 |
365.42 |
93.23 |
|
|
0.00 |
|
120.91 |
|
10403.15 |
252.64 |
47 |
|||
11 |
Vц = 700 |
м/с |
956.60 |
264.03 |
104.53 |
|
0.00 |
|
123.54 |
|
10498.37 |
237.79 |
46 |
||||
12 |
Vц = 750 |
м/с |
912.80 |
214.31 |
110.46 |
|
0.00 |
|
120.83 |
|
10557.12 |
230.57 |
51 |
||||
13 |
Vц = 800 |
м/с |
873.37 |
168.90 |
116.43 |
|
0.00 |
|
118.09 |
|
10604.48 |
224.48 |
58 |
||||
14 |
Vц = 850 |
м/с |
837.74 |
127.23 |
122.48 |
|
0.00 |
|
115.32 |
|
10642.92 |
219.38 |
67 |
||||
15 |
Vц = 900 |
м/с |
805.44 |
88.81 |
128.59 |
|
0.00 |
|
112.52 |
|
10670.57 |
215.16 |
77 |
||||
16 |
Vц = 950 |
м/с |
776.09 |
53.25 |
134.80 |
|
0.00 |
|
109.67 |
|
10691.31 |
211.74 |
90 |
||||
17 |
Vц = 1000 |
м/с |
749.38 |
20.21 |
141.13 |
|
0.00 |
|
106.77 |
|
10704.76 |
209.05 |
106 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 2.18 |
|
|
|
|
Анализ результатов в зависимости |
|
|
||||||||||||
|
|
|
от взаимного расстояния цель-истребитель |
|
|
||||||||||||
|
|
|
|
10 6 , |
10 8 |
|
|
|
|
||||||||
№ |
Параметр |
ц, с |
кр, с |
|
N, с |
|
пас, с |
|
|
, |
|
Gост, кг |
|
X, км |
Число |
||
|
|
|
|
|
|
итераций |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
r0 = 100 |
км |
|
|
|
Задача не имеет решения |
|
|
|||||||||
2 |
r0 = 200 |
км |
663.70 |
181.98 |
|
0.00 |
|
0.00 |
|
146.12 |
|
9444.15 |
|
74.55 |
16 |
||
3 |
r0 = 300 |
км |
873.83 |
392.10 |
|
0.00 |
|
0.00 |
|
139.64 |
|
9364.88 |
|
129.36 |
18 |
||
4 |
r0 = 400 |
км |
1085.47 |
603.75 |
|
0.00 |
|
0.00 |
|
136.90 |
|
9280.16 |
|
183.24 |
19 |
||
5 |
r0 = 500 |
км |
1297.63 |
815.91 |
|
0.00 |
|
0.00 |
|
135.37 |
|
9188.96 |
|
236.81 |
18 |
||
6 |
r0 = 600 |
км |
1510.03 |
1028.31 |
|
0.00 |
|
0.00 |
|
134.40 |
|
9089.53 |
|
290.26 |
18 |
||
7 |
r0 = 700 |
км |
1722.57 |
1240.84 |
|
0.00 |
|
0.00 |
|
133.73 |
|
8979.36 |
|
343.63 |
18 |
||
8 |
r0 = 800 |
км |
1935.18 |
1453.45 |
|
0.00 |
|
0.00 |
|
133.23 |
|
8854.96 |
|
396.95 |
20 |
||
9 |
r0 = 900 |
км |
2147.84 |
1666.12 |
|
0.00 |
|
0.00 |
|
132.86 |
|
8711.56 |
|
450.25 |
19 |
||
10 |
r0 = 1000 |
км |
2360.54 |
1878.82 |
|
0.00 |
|
0.00 |
|
132.56 |
|
8542.86 |
|
503.53 |
20 |
||
11 |
r0 = 1100 |
км |
2573.27 |
2091.54 |
|
0.00 |
|
0.00 |
|
132.31 |
|
8341.08 |
|
556.80 |
19 |
||
12 |
r0 = 1200 |
км |
2786.01 |
2304.29 |
|
0.00 |
|
0.00 |
|
132.11 |
|
8097.88 |
|
610.06 |
20 |
||
13 |
r0 = 1300 |
км |
2998.77 |
2517.04 |
|
0.00 |
|
0.00 |
|
131.95 |
|
7806.31 |
|
663.31 |
20 |
||
14 |
r0 = 1400 |
км |
3211.54 |
2729.81 |
|
0.00 |
|
0.00 |
|
131.80 |
|
7463.52 |
|
716.55 |
20 |
||
15 |
r0 = 1500 |
км |
3424.32 |
2942.59 |
|
0.00 |
|
0.00 |
|
131.68 |
|
7071.96 |
|
769.79 |
20 |
||
16 |
r0 = 1600 |
км |
3637.10 |
3155.38 |
|
0.00 |
|
0.00 |
|
131.57 |
|
6638.33 |
|
823.02 |
22 |
||
17 |
r0 = 1700 |
км |
3849.90 |
3368.17 |
|
0.00 |
|
0.00 |
|
131.47 |
|
6170.98 |
|
876.25 |
24 |
||
18 |
r0 = 1800 |
км |
4062.69 |
3580.97 |
|
0.00 |
|
0.00 |
|
131.39 |
|
5677.76 |
|
929.48 |
20 |
||
19 |
r0 = 1900 |
км |
4275.49 |
3793.77 |
|
0.00 |
|
0.00 |
|
131.32 |
|
5165.13 |
|
982.71 |
21 |
||
20 |
r0 = 2000 |
км |
4488.30 |
4006.57 |
|
0.00 |
|
0.00 |
|
131.25 |
|
4637.95 |
|
1035.93 |
46 |
||
216
|
|
|
|
|
|
|
|
|
Таблица 2.19 |
||
|
|
|
Анализ результатов в зависимости |
|
|
||||||
|
|
|
|
от курса полета цели |
|
|
|
||||
|
|
|
|
10 6 , 10 8 |
|
|
|
||||
№ |
Параметр |
ц, с |
кр, с |
N, с |
пас, с |
, |
Gост, кг |
X, км |
Число |
||
итераций |
|||||||||||
|
|
|
|
|
|
|
|
|
|
||
1 |
0 = 5 |
1858.15 |
1376.42 |
0.00 |
0.00 |
150.25 |
8901.94 |
370.92 |
34 |
||
2 |
0 = 10 |
1868.87 |
1387.14 |
0.00 |
0.00 |
144.54 |
8895.54 |
375.94 |
10 |
||
3 |
0 = 15 |
1894.16 |
1412.44 |
0.00 |
0.00 |
138.87 |
8880.26 |
384.52 |
16 |
||
4 |
0 = 20 |
1935.18 |
1453.45 |
0.00 |
0.00 |
133.23 |
8854.96 |
396.95 |
20 |
||
5 |
0 |
= 25 |
1993.82 |
1512.10 |
0.00 |
0.00 |
127.64 |
8817.54 |
413.73 |
28 |
|
6 |
0 |
= 30 |
2072.94 |
1591.22 |
0.00 |
0.00 |
122.08 |
8764.59 |
435.57 |
42 |
|
7 |
0 |
= 35 |
2176.55 |
1694.82 |
0.00 |
0.00 |
116.58 |
8690.42 |
463.52 |
68 |
|
8 |
0 |
= 40 |
2309.23 |
1827.51 |
0.00 |
0.00 |
111.17 |
8586.26 |
498.95 |
141 |
|
Из полученных результатов видно, что при больших значениях скорости цели задача перехвата методом «маневр» с одним разворотом не имеет решения. Введение в рассмотрение второго разворота позволяет устранить этот недостаток.
Результаты приведены для двух комбинаций значений , . Комбинация 10 1 , 10 2 позволяет получить результат с требуемой точностью, а комбинация 10 6 , 10 8 – практически
точное решение. Как видно, использование таких значений точности позволяет получить требуемый результат с требуемой точностью и меньшим числом итераций. Так, число итераций можно уменьшить в 2–3 раза по сравнению с числом итераций, требуемым для нахождения, практически, точного решения.
2.8. Оптимальное размещение формуляров объектов на электронной карте
На электронных картах стационарные объекты отображаются с формулярами, положение которых устанавливается вручную при большом масштабе карты, поэтому перекрытий формуляров не наблюдается. Когда масштаб карты уменьшается, формуляры начинают перекрываться друг другом и объектами, поэтому наглядность картины ухудшается. Если изменить положение формуляров, то диапазон масштабирования можно расширить за счет уменьшения масштаба карты.
217
Если появятся нестационарные объекты, которые будут перемещаться по карте в различных направлениях, необходимо будет разместить их формуляры, чтобы перекрытий не наблюдалось или их количество было наименьшим. Причем этот процесс должен быть автоматическим, так как задание вручную положений формуляров долгий процесс, за время которого объекты могут сильно изменить положение относительно первоначального.
В данном разделе приводится алгоритм оптимальной расстановки формуляров объектов, располагающихся в ограниченной области вокруг объекта, при их минимальных пересечениях [29].
На карте объектам и формулярам отводятся прямоугольные области, которые содержат условное изображение объекта и идентификационные надписи соответственно
(рис. 2.22).
Формуляр не должен быть удален от своего объекта не более чем на заданное расстояние d_max .
Тогда система ограничений имеет вид
|
|
xj Xi |
|
|
w; |
i, |
j 1,..., N; |
|
||||||
|
|
|
||||||||||||
|
|
yi Yi |
|
h; |
|
|
|
|
(2.271) |
|||||
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
(X |
i |
x )2 |
(Y |
y )2 |
d_max |
, |
||||||
|
|
|
|
|
|
|
|
i |
|
i |
i |
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где xj, yj – координаты центров прямоугольников, соответствующих объектам (далее объекты); Xi, Yi – координаты центров прямоугольников, соответствующих формулярам (далее формуляры); w – ширина прямоугольника; h – высота прямоугольника (предполагаем, что размеры объектов и формуляров равны); N – количество точек; d_maxi – величина расстояния, дальше которого формуляр
не может находиться от объекта.
Минимизируемая функция построена следующим образом [51]:
|
1 |
|
|
N |
N |
|
F(X1,Y1,..., XN ,YN ): |
|
Smn |
di |
0.001 dik , (2.272) |
||
2 |
||||||
|
|
(m, n) |
i 1 |
i 1 k |
где Smn – площадь перекрытия формуляров m и n; di – расстояние от центра формуляра до соответствующего ему объекта; dik – расстоя-
218
ние от центра формуляра i до объектов, лежащих в области P, которая представляет собой круг радиуса d_maxi с центром в i-м объекте; k – индексы тех объектов, которые лежат в области P.
Для минимизации был выбран метод покоординатного спуска с последующей пошаговой минимизацией по координатам. Результаты минимизации такой целевой функции для двух примеров изображены на рис. 2.23 – 2.26.
Рис. 2.23. Начальная расстановка
Рис. 2.24. Результат оптимизации
219
Рис. 2.25. Начальная расстановка
Как видно из рис. 2.24 и 2.26, картина значительно улучшилась по сравнению с тем, что было до оптимизации. Каждый формуляр читается и практически каждый формуляр расположен около соответствующего ему объекта, так что можно легко определить какому объекту принадлежит формуляр.
Наличие ограничений на перекрытие формуляра и объектов вида (2.271), во-первых, усложняют вычислительный алгоритм, тем самым увеличивая время его работы, во-вторых, эти ограничения предъявляют высокие требования к заданию начальных условий: если изначально какой-нибудь формуляр перекрывает объект, то алгоритм работать не будет.
Исключить неравенства, соответствующие перекрытиям, можно методом штрафных функций (см. п. 1.4.1). В качестве штрафных функций будем использовать площади перекрытия между формуляром и объектами, лежащими в круге радиуса d_max с центром в объекте, соответствующем данному формуляру. Прибавив к минимизируемой функции сумму этих площадей, получим, что при минимизации формуляр будет стремиться «выйти за пределы объекта».
220
Рис. 2.26. Результат оптимизации
Таким образом, задача примет вид: найти минимум функции F(X1, Y1, …, XN, YN) при ограничениях
(X |
i |
x )2 |
(Y |
y )2 |
d_max |
i |
, |
(2.273) |
|
i |
i |
i |
|
|
|
где xj, yj – координаты центров объектов; Xi, Yi – координаты центров формуляров; N – количество точек; d_maxi – расстояние, дальше которого формуляр i не может находиться от объекта.
Минимизируемая функция имеет вид
|
|
|
|
1 |
|
|
|
|
|
N |
|
|
|
N |
|
|
|
|
|
|
|
F(X |
,Y ,..., X |
N |
,Y ): |
|
|
|
S |
mn |
|
|
d |
i |
0.001 |
|
|
d |
ik |
|
|
S |
, |
|
|||||||||||||||||||||
1 |
1 |
N |
2 |
|
|
|
|
|
|
|
|
|
ik |
||||||||
|
|
|
|
|
(m, n) |
|
|
i 1 |
|
|
|
i 1 |
k |
|
|
|
k |
|
|
||
(2.274)
где Smn – площадь перекрытия m и n формуляров; di – расстояние от центра формуляра до соответствующего ему объекта; dik – расстояние от центра i-го формуляра до объектов, лежащих в области P, которая представляет собой круг радиуса d_maxi с центром в i-м объекте; k – индексы тех объектов, которые лежат в области p; Sik – площадь перекрытия i формуляра и k объекта.
221

Результат оптимизации при начальных условиях, изображенных на рис. 2.25, представлен на рис. 2.27.
Как видно из рисунка, наглядность картины не ухудшилась – все формуляры хорошо видны. Время расчета сократилось на 35 %.
Рис. 2.27. Результат оптимизации с применением штрафной функции
Алгоритм оптимизации состоит из трех шагов [45].
1.Минимизация покоординатным спуском с последующей пошаговой минимизацией по координатам. Шаг в процессе минимизации по координатам остается постоянным и равным единице. При большем шаге высока вероятность нарушения ограничения. А меньшее значение шага не имеет смысла, так как этот шаг определяет разрешающую способность монитора.
2.Минимизация покоординатным спуском с применением «отражения» прямоугольников.
3.Минимизация покоординатным спуском с последующей пошаговой минимизацией по координатам. Шаг в процессе минимизации по координатам остается постоянным и равным единице.
222
Как следует из алгоритма, в качестве метода минимизации функции (2.274) вновь использовался метод покоординатного спуска с последующей пошаговой минимизацией по координатам. Данный метод прост в вычислительном плане, что сокращает время работы алгоритма. Пошаговая минимизация выбрана потому, что хорошо работает на заданных ограничениях.
Процедура «отражения» прямоугольников заключается в том, что после применения метода покоординатного спуска и достижения им минимума, каждый прямоугольник зеркально отражается относительно соответствующей ему точки сначала по координате х, потом по у. После отражения по какой-либо координате проверяются соответствующие ограничения и вычисляется значение критерия. Если ограничения не нарушены и критерий уменьшился, то «отражение» происходит окончательно, в противном случае – нет. Отражение по одной из координат показано на рис. 2.28.
Математически эту процедуру можно записать
Shag = xi – Xi, Xi = Xi + 2*Shag, |
(2.275) |
где Xi, Yi – координаты центра формуляра; xi, yi – координаты центра объекта.
2.9.Оптимизация режима работы ядерного реактора
впеременном суточном графике нагрузки
сучетом возможности утилизации энергии
Вп. 2.2 рассматривалась задача оптимизации работы системы реакторов в переменном суточном графике нагрузки. При этом АЭС с реакторами серийных типов (ВВЭР, РБМК) по ряду причин не в состоянии обеспечить переменный суточный график нагрузки
вполном диапазоне без серьезного ущерба для экономических показателей и надежности энергоустановки. Допустимый диапазон суточных колебаний мощности и скорость набора нагрузки для этих реакторов значительно ниже, чем требуется по условиям работы энергосистем с разуплотненным графиком нагрузки.
223
В качестве одного из эффективных решений названной проблемы предполагается создание на базе АЭС энергокомплексов, включающих установки, способные воспринять и полезно использовать избыток энергии, вырабатываемой АЭС в период снижения ее потребления в энергосистеме. В качестве устройств, использующих избыточную энергию, могут рассматриваться утилизаторы, обеспечивающие производство другого ценного продукта (водорода, синтетического или жидкого топлива) или энергоснабжение потребителей низкопотенциальным теплом. Не останавливаясь детально на конкретных схемах утилизации энергии, рассмотрим возможности оптимизации работы комплекса «реактор-утилизатор» с точки зрения эффективности использования ядерного топлива[68].
Физическая предпосылка оптимизации заключается в том, что с одной стороны, если переменный график работы энергосистемы полностью отрабатывается реактором, то это может привести к резервированию дополнительного запаса реактивности, а следовательно, и увеличенному расходу топлива. С другой стороны, если реактор работает в базовом режиме, а переменный график обеспечивается работой утилизатора, то можно ожидать, что при низкой эффективности утилизатора также произойдет увеличенный расход ядерного топлива. Таким образом, возникает задача об оптимальном режиме работы энергокомплекса.
2.9.1. Постановка задачи
Имеется ядерный энергоблок номинальной тепловой мощностью WH [МВт]. Известно, что по условиям работы энергосистемы
потребуется эксплуатация этого энергоблока в переменном суточном графике нагрузки. При этом задаются следующие параметры графика нагрузки:
1)время работы на пониженной мощности [сут];
2)уровень пониженной мощности WH (0 1).
Для повышения эффективности работы энергоблока предполагается возможность утилизации части энергии с коэффициентом полезного действия QA /QB , где QA - полезная энергия, отда-
ваемая утилизатором, QB - полная энергия, отпущенная на утилизацию. Каков должен быть режим работы ядерного реактора, чтобы
224

расход топлива на единицу отпущенной потребителю энергии был минимален?
Рассмотрим следующую ситуацию. Пусть в момент времени t=0 мощность реактора снижается до уровня WH , где 1. Поскольку в систему требуется поставить энергию, соответствующую работе на более низком уровне мощности WH , то излишек энер-
гии в количестве Q WH ( ) передается утилизатору (рис.2.29). Из этой энергии потребителю будет отпущена часть, равная QA WH ( ). Таким образом, реактор за одни су-
тки (один цикл) вырабатывает энергию в количестве:
QP WH (1 ) WH ,
а потребителю будет отпущена лишь часть энергии:
En WH (1 ) WH ( ) WH .
Расход топлива при работе реактора в таком режиме – G. Эта величина определяется отношением полной энергии, произведенной реактором за сутки к глубине выгорания топлива:
G WH (1 ) WH .
Pt( )
W |
Wн |
на утилизацию |
|
Wн |
QA |
||
|
|||
|
|
Q
Wн
Рис. 2.29. Режим работы энергокомплекса с утилизацией энергии
Тогда расход топлива на единицу энергии, отпущенной потребителю равен
225
g( ) |
G |
|
WH (1 ) WH |
, (2.276) |
|||
E |
n |
Pt( ) [(1 ) W |
W |
( ) W ] |
|||
|
|
|
H |
H |
H |
|
|
где Pt( )- глубина выгорания топлива при работе реактора в переменном графике нагрузки с ежесуточной разгрузкой до уровня
мощности Wн ( 1).
Глубина выгорания топлива Pt( )зависит от резервируемого запаса реактивности, дающего возможность снизить мощность реактора до величины WH . Для реактора с непрерывной перегруз-
кой топлива и для корпусных реакторов в конце кампании, между глубиной выгорания топлива и величиной запаса реактивности справедливо соотношение:
Pt( ) Ptb |
p( ) , |
(2.277) |
|
q |
|
где Ptb – глубина выгорания топлива при работе реактора в базовом режиме на номинальной мощности [ МВт сут/т U]; q – коэф-
фициент пропорциональности, зависящий от физических свойств активной зоны реактора [ т U/МВт сут]; p( ) – запас реактив-
ности на преодоление нестационарного ксенонового отравления при снижении мощности до уровня Wн .
К сожалению, в явном виде зависимость p( ) получить не уда-
ется. Однако можно показать, что данная зависимость с погрешностью не более 3% аппроксимируется функцией вида
p( ) |
1 |
|
y |
, |
(2.278) |
|
B C |
f |
|||||
|
|
|
|
где y – выход йода на одно деление; f – среднее число вторич-
ных нейтронов на акт деления; B 0.52, C 0.977 – константы аппроксимации.
Подставляя эту зависимость в соотношение (2.276) и (2.277), получим явный вид минимизируемой функции:
g( ) |
|
|
|
|
|
|
1 |
. (2.279) |
|||
(Pt |
б |
|
1 |
|
y |
) (1 |
( ) ) |
||||
|
|
||||||||||
|
B C |
f |
q |
|
|||||||
|
|
|
|
|
|
|
|||||
Оптимизационная задача ставится следующим образом:
226
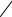
до какого уровня от номинала * следует снижать мощность реактора, чтобы при заданных параметрах энергокомплекса (КПД утилизатора и плотности потока нейтронов в реакторе) расход топлива на единицу отпущенной энергии был минимален?
В математическом плане данная задача относится к классу задач нелинейного программирования: найти
min{g( ) |
|
|
|
|
|
1 |
} (2.280) |
|||
(Pt |
|
1 |
|
y |
) (1 |
( ) ) |
||||
|
|
|||||||||
|
B C |
f |
q |
|
||||||
|
б |
|
|
|
|
|
||||
при ограничении 1.
2.9.2. Анализ оптимального режима
Для получения численных результатов был рассмотрен энергоблок со следующими характеристиками (близкими к характеристикам реактора РБМК-1000):
номинальная тепловая мощность реактора WH 3200МВт;
коэффициент q 1,02 10 5 , |
т U/МВт сут; |
время разгрузки 13 , сут.
Константы аппроксимации В и С однозначно определяются уровнем плотности потока нейтронов. Рассмотрим следующие варианты:
1) 5 1013 |
нейтр |
; |
2) 3 1013 |
нейтр |
. |
см2 с |
|
||||
|
|
|
см2 с |
||
На рис. 2.30 показана зависимость оптимальной степени снижения мощности энергоблока от КПД утилизатора при 0,3 и различных значениях . Из результатов, представленных на ри-
сунке, следует, что если КПД утилизатора менее 60 %, то оптимально вообще от него отказаться и отрабатывать переменный суточный график нагрузки путем соответствующего изменения мощности реактора. Напротив, если предполагается использовать утилизатор с КПД более 80 % , то оптимальным режимом является базисный режим работы реактора с передачей всего излишка вырабатываемой энергии на утилизатор. Если КПД утилизации находится
227
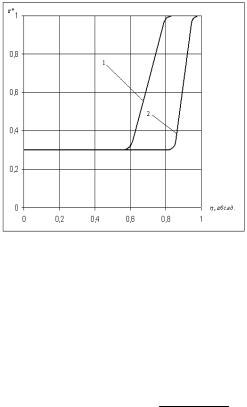
в пределах 60-80 %, то оптимальным является режим с частичной разгрузкой энергоблока и частичной утилизацией энергии.
Рис. 2.30. Зависимость оптимальной степени снижения мощности реактора от КПД утилизатора при различных плотностях потока нейтронов
1 – |
5 1013 |
нейтр2 ; |
|
|
см. с |
2 – |
13 |
нейтр |
3 10 |
см.2с |
Ход кривой ( ) имеет простое физическое объяснение. С ростом увеличивается доля полезной энергии при утилизации QA . В
этом случае выгодно передавать больше энергии на утилизацию. С увеличением плотности потока нейтронов растет запас реактивности на компенсацию ксенонового отравления и снижать уровень
мощности в реакторе становится менее выгодным ( – растет). Об эффективности оптимизации режима работы энергоком-
плекса «реактор – утилизатор энергии» можно судить по величине
S gmax gопт 100% ,
gmax
где gmax – максимальный удельный расход топлива для отработки переменного графика нагрузки «антиоптимальным» способом; gопт - минимальный удельный расход топлива при оптимальном
уровне снижения мощности.
Величина S зависит от таких параметров, как номинальная плотность потока нейтронов в реакторе, КПД утилизации, время работы на пониженной мощности и уровень снижения мощности. Расчеты показывают, что эффективность при различных КПД и потоках изменяется от 0,2 до 7 %.
228
При этом для энергокомплекса с параметрами, близкими к ре-
ально возможным ( (5 7) 1013 |
нейтр |
; |
60 80 %), опти- |
2 |
|||
|
см. с |
|
|
мальным является компромиссный режим, при этом эффект от оптимизации составляет величину 0.2 – 0.3 %.
2.10. Оптимизационные задачи при наличии негерметичных тепловыделяющих сборок в РБМК
При работе реактора типа РБМК возможны ситуации, когда одна или несколько тепловыделяющих сборок в процессе эксплуатации становятся негерметичными. Для обнаружения этого факта предназначена система контроля герметичности оболочек твэл (СКГО) [10]. Существующие санитарные правила проектирования и эксплуатации атомных электростанций определяют величину предельного допустимого уровня выброса (ПДВ). Например, в случае достижения годового ПДВ ранее 1-го календарного года АЭС должна быть остановлена [46]. В связи с этим возникает ряд задач, связанных с обнаружением и порядком выгрузки негерметичных ТВС.
Во-первых, если в данный момент времени обнаружено несколько негерметичных ТВС различной энерговыработки с различными интенсивностями выбросов, причем суммарный выброс не превышает предельно допустимого уровня, то возникает задача определения очередности выгрузки негерметичных ТВС, таким образом, чтобы потеря суммарной энерговыработки была минимальной, не превысив при этом предельно-допустимый уровень.
Во-вторых, если предельно допустимый уровень радиации превышен, но превышение не носит «катастрофического» характера, то предлагается приписать эксплуатационникам «штраф» за нахождение негерметичной ТВС в активной зоне. Величина штрафа при этом пропорциональна выброшенной в окружающую среду активности продуктов деления за время нахождения негерметичной ТВС в активной зоне.
Сразу же отметим, что в настоящее время на АЭС могут наложить штрафные санкции только за превышение установленных нормативных выбросов и/или сбросов. Такого превышения, как
229
правило, не достигается даже при наличии в активной зоне реакторов 1-2 негерметичных ТВС.
Выгрузка связана обычно с превышением пределов по активности, установленных самой АЭС, которые в несколько раз меньше нормативных. Ущерб от преждевременной выгрузки ТВС можно оценивать либо в натуральном показателе – как потерю энерговыработки, либо в денежном эквиваленте – как потерю стоимости ТВС данной энерговыработки при невозможности ее дожигания. Дело в том, что после выгрузки любой ТВС по негерметичности проводятся «пенальные испытания» (через 3 дня после выгрузки).
При не подтверждении факта негерметичности и после осмотра телекамерами ТВС может быть загружена обратно в активную зону через 5 – 10 дней. В этом случае потери сводятся к трудозатратам на лишнюю перегрузку ТВС и пробоотбор, кроме того наблюдается ухудшение нейтронно-физических характеристик реактора при работе с лишним столбом воды в топливном канале. Часто возможны повреждения ТВС при перегрузке в бассейн выдержки и неоднозначные результаты пробоотбора, в результате чего ТВС не возвращается в активную зону.
Ниже предлагается несколько постановок и решений оптимизационных задач, основанных как на подходе безусловного не превышения уровня предельно допустимого выброса, так и на подходе наложения штрафных санкций в случае его превышения.
2.10.1. Задача выбора оптимальной очередности извлечения негерметичных ТВС при ограничении на предельно-допустимый уровень выброса активности
Пусть, обнаружено, что негерметичными являются N ТВС. При этом каждая ТВС к этому моменту имеет энерговыработку E0i , время работы t0i и интенсивность выброса xi . Если i -ю ТВС оставить в активной зоне еще на время ti , то энерговыработка составит величину E(t0i ti). Пусть максимальное значение энерговыработки Em тепловыделяющая сборка достигает в момент времени tm . При выгрузке ТВС через время ti , потеря энерговыработки i-й ТВС составит величину Ei Em E(t0i ti). Сум-
230
марная потеря энерговыработки при выгрузке всех негерметичных
N
ТВС есть S Ei ( ti ) . Требуется найти такую очередность вы-
i 2
грузок ТВС, то есть t1,... tN , чтобы минимизировать суммарную потерю энерговыработки и при этом не нарушить ограничение на величину суммарного выброса активности P .
Математически задача ставится следующим образом: Найти
N |
|
|
min Ei ( ti ) , |
(2.281) |
|
t1... tN i 1 |
|
|
при ограничениях: |
|
|
N |
|
|
xi ti P, |
(2.282) |
|
i 2 |
|
|
0 ti |
tm toi , |
(2.283) |
|
xi 0. |
(2.284) |
Задача (2.281) – (2.284) может быть решена аналитически при следующих предположениях. Пусть мощность топливного канала зависит от времени линейно
W(t) Wm wt , |
(2.285) |
где Wm - средняя мощность свежезагруженной ТВС, w - коэффи-
циент. Тогда зависимость средней энерговыработки от времени есть
t |
|
w |
t2 . |
|
|
E(t) W(t)dt Wm |
t |
(2.286) |
|||
2 |
|||||
0 |
|
|
|
||
|
|
|
|
В этом случае с учетом выражений (2.285), (2.286) оптимизационная задача выглядит следующим образом: Найти
|
N |
|
|
W |
2 |
|
|
|
|
|
W |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
min Em |
E0i |
|
0i |
|
|
w |
ti |
|
0i |
|
|
|
, |
||
|
|
|
|
||||||||||||
|
|
|
|
2 w |
|
2 |
|
|
w |
|
|
|
|||
t1... tN |
i 1 |
|
|
|
|
|
|
|
|
||||||
При ограничениях
N
xi ti P,
i 1
где W0i Wm wt0i
Рассмотрим решение задачи для двух переменных:
(2.287)
(2.288)
231
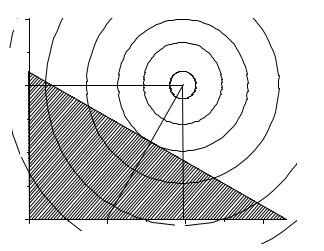
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
W01 |
|
2 |
|
2 |
|
|
|
|
|
W02 |
2 |
||||
min |
S 2E |
|
E |
W01 |
|
w |
t |
|
|
E |
W02 |
|
w |
t |
|
, |
||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
m |
|
01 |
2 w |
|
2 |
|
1 |
w |
|
02 |
2 w |
|
2 |
|
2 |
w |
|
|||||||||||
t1... tN |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x1 t1 x2 t2 |
P , |
|
|
|
|
|
|
|
|
(2.289) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2.290) |
|||||||||||||
где |
W01 |
t |
m |
t |
01 |
T и |
|
W02 |
t |
m |
t |
02 |
T – |
соответственно ин- |
||||||||||||||||
|
||||||||||||||||||||||||||||||
|
w |
|
|
|
|
1 |
|
|
|
w |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
тервалы времени от момента обнаружения негерметичности до момента штатной выгрузки при максимальной энерговыработке Em . Отсюда вытекают ограничения:
(2.291)
(2.292)
Оптимизационная задача (2.289) – (2.292) имеет простую геометрическую интерпретацию.
Функция z S( t1, t2) представляет собой параболоид вращения, ограничение x1 t1 x2 t2 P описывают плоскость, параллельную оси z . На рис. 2.31 показаны проекции плоскости и горизонтальных сечений параболоида на плоскость ( t1, t2 ).
Оптимальное время работы второй ТВС
t* |
|
|
2 |
|
|
P/x2 |
A |
|
|
||
|
||
|
|
B
L P/x1
C |
D |
|
* |
|
|
|
t1 |
|
ОптимальноевремяработыпервойТВС |
|
|
Рис. 2.31. Геометрическая интерпретация задачи оптимизации
232
Из рисунка видно, что оптимальным является точка касания прямой и окружности, если эта точка находится внутри области. В противном случае оптимальное решение лежит на границе области допустимых значений. Для внутренних точек области изменения переменных оптимальное решение находится из соотношений:
S |
0; |
S |
|
0 . |
(2.293) |
|
t |
t |
2 |
||||
|
|
|
||||
1 |
|
|
|
|
В явном виде оптимальные значения t1 и t2 будут и меть вид
|
|
|
W01 |
|
|
|
x1 |
|
|
|
|
|
|
|
P |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
W02 |
|
|
|
|
|
|
x1 |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
t |
* |
w |
|
|
x2 w |
|
x2 x2 |
, |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
x1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
x1 |
|
2 |
|
|
|
|
x1 |
|
W01 |
|
P |
|
|||||||||||
|
|
|
|
|
|
|
|
|
W02 |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
|||||||||||||||||
|
* |
|
x2 |
w |
x2 |
w |
. |
||||||||||||||||||||||
|
t2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
x1 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|||
(2.294)
(2.295)
Исключая из выражений (2.294) – (2.295) член Р/х2, получим уравнение оптимальной траектории:
t* |
|
x2 |
|
t* |
|
W02 |
|
|
|
W01 |
|
|
|
x2 |
|
, |
(2.296) |
||||
|
|
|
|
|
|
|
|
|
|||||||||||||
2 |
|
1 |
|
|
w |
|
|
w |
|
|
|
|
|||||||||
или |
x1 |
|
|
|
|
|
|
|
|
|
|
x1 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
* |
|
|
x2 |
|
* |
|
|
|
|
|
|
|
|
|
x2 |
|
(2.297) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
t2 |
x |
|
t1 T2 |
T1 x |
. |
|||||||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|||
Возможные оптимальные траектории представлены на рис. 2.32. Характер оптимальных траекторий понимается следующим образом. Если интенсивность выбросов такова, что предельно допустимый уровень выброса не превышается до момента штатной перегрузки обеих ТВС, то оптимальным является решение
t* T ; |
t |
* T |
2 |
− точка A, т.е. обе ТВС дожигаются до |
|
1 |
1 |
|
2 |
|
|
штатной энерговыработки. В противном случае ТВС должны выгружаться ранее (траектории ABC,AC,ADC ).
233
Рис. 2.33. Вид возможных оптимальных траекторий |
|
||||
|
|
|
|
|
|
Если T2 T1 |
x2 |
|
0 , то оптимальные точки лежат на траек- |
||
|
|||||
x1 |
|
|
|
|
|
тории АВС. Физически это означает, что если, например, |
x2 |
1, |
|||
|
|||||
|
|
|
x1 |
|
|
тогда T2 T1, т.е. вторая ТВС более «свежая», и время ее пребывания в активной зоне до выгрузки больше, чем более выгоревшей ТВС ( t2* t1* ). На участке траектории BC первая ТВС вы-
гружается сразу же, а вторая «дожигается», пока не нарушится ограничение по выбросу активности.
Если |
T |
T |
|
|
|
x2 |
|
0, то ситуация носит противоположный |
|
|
|
||||||
|
2 |
1 |
|
|
|
|||
|
|
|
|
x1 |
|
|
||
характер (траектория ADC). |
||||||||
|
|
|
|
|
|
|
||
При |
T2 |
T1 |
|
|
x2 |
|
0 (траектория AC ) обе ТВС некоторое |
|
|
||||||||
|
|
|
|
x1 |
|
|
||
время находятся в активной зоне, и отношение оптимальных времен пребывания ТВС в активной зоне будет определяться как
234
t2* T2 . Менее выгоревшая ТВС дольше находится в активной
t1* T1
зоне. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x1 |
|
|
|
|
При |
произвольном |
|
соотношении |
|
|
|
|
активностей |
|
и |
значений |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
x2 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
времен T1, T2 |
ответ не является очевидным и определяется из |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
соотношений: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
P |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
1) |
при T1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
T2 |
|
|
|
|
|
|
|
|
|
|
|
0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
x2 x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
* |
|
|
|
|
|
|
|
|
|
|
|
* |
|
|
|
|
|
|
|
P |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 0t, |
|
t2 |
|
|
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
2 |
|
|
|
|
|
|
|
x1 |
|
|
|
|
|
|
|
|
|
|
|
|
P |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
2) |
|
x1 |
|
T2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
при |
|
|
|
|
|
|
|
|
T1 |
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
x2 |
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
* |
|
0t, |
|
|
t* |
P |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
3) |
при |
|
|
x |
|
|
|
|
|
|
|
P |
x |
|
|
|
|
|
и |
x |
2 |
|
|
|
x |
|
|
|
|
|
P |
|
, |
|||||||||||||||||||||||||||||
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
0 |
|
|
|
|
1 |
|
T |
|
1 |
|
|
|
|
|
|
0 |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
T |
|
x |
|
T |
|
|
x |
x |
|
|
|
|
|
|
|
x |
|
x |
|
|
|
T |
x |
|
|||||||||||||||||||||||||||||||||||||
|
|
|
1 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
1 |
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
2 |
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P |
|
|
x |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T1 |
|
|
|
|
T2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
t |
* |
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
x2 |
|
, |
|
|
|
(2.298) |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x1 |
2 |
|
|
|
|
|
|
|
|
x1 |
|
|
|
|
|
|
|
P |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
* |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T1 |
|
x2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
t |
|
|
x2 |
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
(2.299) |
||||||||||||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Например, |
пусть T |
|
tm |
|
, |
T |
|
|
|
|
tm |
|
, |
|
|
|
P |
|
tm |
. |
|
|
Иными слова- |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
x2 |
|
8 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
ми, первая ТВС отработала всего половину кампании, а вторая – три четверти кампании.
235
Если |
x1 |
1, то, |
t* |
|
3 |
t |
m |
, * 0t – в активной зоне остается |
|
x2 |
|
1 |
16 |
|
2 |
||
менее выгоревшая ТВС, другая выгружается сразу же при обнару-
жении негерметичности. Если |
x1 |
5, то |
1* 0t, |
t2* |
tm |
– ме- |
|
x2 |
|
|
8 |
|
|
нее выгоревшая ТВС выгружается сразу, а другая остается в активной зоне, пока не нарушится ограничение.
Наконец, если |
x1 |
3, то |
t* |
1 |
t |
m |
, t |
* |
7 |
t |
m |
– обе ТВС |
|
x2 |
|
1 |
80 |
|
|
2 |
80 |
|
|
некоторое время дожигаются в активной зоне.
2.10.2.Задача выбора ТВС для выгрузки по негерметичности
сучетом штрафа
Предположим, что по данным системы КГО подозреваются в негерметичности типа «газовой неплотности» несколько ТВС. Пусть стоимость ТВС с энерговыработкой E определяется по соотношению [23]:
C Ce(1 |
3 E |
|
1 |
( |
E |
) |
2 |
) . |
||
|
|
|
|
|
|
|||||
2 Em |
2 |
Em |
|
|||||||
|
|
|
|
|
|
|||||
Если на самом деле ТВС герметична, но выгружается в момент времени t0 (время отсчитывается от момента загрузки данной
ТВС в реактор), то ущерб от преждевременной выгрузки можно выразить как
S1 |
Ce i(1 |
3 Ei(t0) |
|
1 |
( |
Ei (t0) |
) |
2 |
), |
(2.300) |
||
|
|
|
|
|
|
|||||||
2 Em |
2 |
Em |
|
|||||||||
|
|
|
|
|
|
|
|
|||||
где Em – энерговыработка ТВС, выгружаемой по плану перегрузок; –- энерговыработка i-й ТВС, выгружаемой по подозрению в негерметичности в момент времени t0 ; Ce – коэффициент, пере-
водящий потерю энерговыработки в денежный эквивалент. При этом выброса активности в атмосферу нет; – вероятность невозврата i-й ТВС в активную зону для дожигания, вследствие технологических причин, например, механических повреждений.
236
Если же ТВС негерметична, но остается в активной зоне течение времени ti до момента перегрузки, то ущерб за счет штрафа от превышения естественного фона будет выражаться соотношением
|
ti |
|
|
S2 Cf x( )d , |
(2.301) |
|
0 |
|
где x( ) |
– величина превышения активности над фоновым значе- |
|
нием xf |
, при котором ТВС считается герметичной; Cf |
– коэффи- |
циент, переводящий превышение активности над естественным фоном в денежный эквивалент.
Пусть i – вероятность того, что данная i-я ТВС негерметична в момент времени t0 .
Тогда средний ущерб от принятия ошибочного решения по i-й ТВС
S (1 )S S (1 ) C (1 |
3 |
|
Ei |
|
1 |
( |
Ei |
)2) |
||||
|
|
2 |
|
|||||||||
i |
i 1 |
i |
2 |
i i e |
2 E |
|
E |
|||||
|
|
|
|
|
|
|
m |
|
|
m |
||
|
|
ti |
|
|
|
|
|
|
|
|
|
|
|
i Cf |
xi ( )d . |
|
|
|
|
|
|
(2.302) |
|||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
Понятно, что вероятность того, что ТВС является негерметичной, может зависеть от нескольких факторов, например: от количества перегрузок данной ТВС, от нарушений ограничений по величине линейной нагрузки, мощности, расхода теплоносителя, от месторасположения ТВС в активной зоне, от амплитуды и частоты высотных колебаний энерговыделения и т.д. Предположим, что для каждой ТВС известна вероятность выхода по негерметичности и рассмотрим вариант, когда она не зависит от энерговыработки [28]. Если считать, что активность i-й ТВС не нарастает во времени
ti
(иначе она была бы легко обнаружена), то xi( )d xi ti , где
0
ti – время до штатной перегрузки данной ТВС.
237
Тогда средняя потеря в случае неверного решения «о судьбе» ТВС
S |
i |
(1 |
) |
C |
e |
(1 |
3 |
|
Ei |
|
1 |
( |
Ei |
)2) |
t |
i |
C |
x . |
(2.303) |
|
|
|
|
||||||||||||||||
|
i |
i |
|
2 |
|
Em |
2 |
|
|
i |
|
|
f i |
|
|||||
|
|
|
|
|
|
|
|
Em |
|
|
|
|
|
||||||
Как видно из выражения (2.284), потери при ошибочном решении зависят как от величины активности, так и от конкретного значения энерговыработки данной ТВС.
Таким образом, если на негерметичность данного вида подозревается несколько сборок, то, в первую очередь, должна выгружаться ТВС с меньшим значением Si .
2.10.3. Задача о выборе оптимального времени выгрузки негерметичной ТВС с учетом штрафа
Совершенствование аппаратурных и программных средств КГО повышают вероятность обнаружения негерметичной ТВС [12]. При этом возникает другая задача оптимизации, связанная с временем извлечения негерметичной ТВС.
Предположим, что в момент времени t t0 было обнаружено, что данная ТВС – негерметична. При этом ТВС к этому времени имеет энерговыработку E0 . Если эту ТВС перегрузить немедленно, то за счет недожигания ущерб будет составлять величину S1 (2.303) при =1, поскольку повторное использование данной ТВС невозможно:
S1 |
Ce(1 |
3 Ei(t0) |
|
1 |
( |
Ei (t0) |
) |
2 |
). |
(2.304) |
||
|
|
|
|
|
|
|||||||
2 Em |
2 |
Em |
|
|||||||||
|
|
|
|
|
|
|
|
|||||
Если же оставить данную ТВС в активной зоне на время t , то
потери в энерговыработке уменьшатся за счет дополнительного выжигания топлива в течение времени t , но возрастут потери за
счет штрафа за превышение активности над естественным фоном:
|
t |
|
S2 Cf |
x( )d . |
(2.305) |
|
0 |
|
238
Таким образом, существуют две противоположных тенденции и, следовательно, может существовать такой интервал времениtпосле обнаружения негерметичной ТВС через который и следу-
ет проводить ее замену. Математически задача сводится к поиску такого значения t, при котором функция потерь S принимала
минимальное значение:
|
|
|
|
|
|
|
|
3 |
|
|
Ei (t0 t) |
|
|
||
min(S1 |
S2) min Ce |
(1 |
|
|
|
|
|
. |
|
||||||
2 |
|
|
Em |
|
|
||||||||||
t |
|
t |
|
|
|
|
|
|
|
|
|
||||
|
|
1 |
|
|
E |
(t |
|
t) |
|
|
|
t |
|
|
|
|
|
|
|
0 |
)2) Cf |
|
|
|
|||||||
|
|
|
|
( |
i |
|
|
|
x( )d . |
(2.306) |
|||||
|
2 |
|
|
Em |
|
||||||||||
|
|
|
|
|
|
|
|
|
0 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Легко получить явный вид минимизируемой функции при следующих предположениях: мощность ТВС от времени зависит линейно W(t) W0 w t и превышение сигнала над фоном описы-
вается также линейной функцией x( ) x0 b t . В этом случае Ei(t0 t) W(t0) t и минимизируемая функция примет вид:
|
|
|
|
|
|
3W t |
|
|
|
1 |
|
W t) |
)2) C |
|
|
|
|
b( t)2 |
|
||||||||||
S |
i |
C |
e |
(1 |
|
|
i |
|
|
|
|
( |
|
|
|
i |
|
|
f |
[x |
0 |
t |
|
]. |
|||||
2 |
E |
|
|
2 |
|
|
|
E |
m |
|
2 |
||||||||||||||||||
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Минимум функции находится из условия |
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dS |
|
0 , |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d( t) |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
оптимальное значение t |
есть |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3Wi |
|
p x0 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
topt |
|
|
|
2Em |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
(2.307) |
||||||||||
|
|
|
|
|
|
|
|
|
W |
|
)2 p |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
( |
|
i |
b |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Em |
|
|
|
|
|
|
|
|
|
|
|
|
|||
где p |
Cf |
|
– относительная величина стоимости штрафа за пре- |
||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||
Ce
вышение фона.
Смысл этого выражения очевиден: интервал времени до выгрузки негерметичной ТВС тем больше, чем более свежая ТВС по-
239
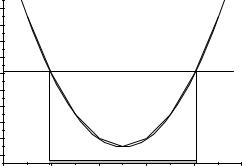
дозревается в негерметичности и тем меньше, чем больше интен- |
|||||
сивность выбрасываемой активности. |
|
|
|
||
Задача может быть поставлена и следующим образом: опреде- |
|||||
лить такую область принятия решений о выгрузке ТВС, при кото- |
|||||
рой ущерб не превышал бы заданной величины Si |
C0 .(рис. 2.34). |
||||
В этом случае имеется свобода в выборе момента выгрузки не- |
|||||
герметичной ТВС, что может быть полезно исходя из технологиче- |
|||||
ских соображений. |
|
|
|
|
|
Si |
|
|
|
|
|
ущерб |
|
|
|
|
С0 |
|
|
|
|
|
|
t0 |
t |
временной интервал |
t |
|
t |
|
2 |
|
|||
|
|
1 |
|
|
|
Рис. 2.34. Зависимость ущерба от времени нахождения негерметичной ТВС |
|||||
|
|
в активной зоне |
|
|
|
Таким образом, представленные выше постановки оптимизационных задач дают возможность либо минимизировать потери при принятии решения о выгрузки негерметичной ТВС, либо оценить их при другом решении, отличном от оптимального.
240

СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
1.Аоки М. Введение в методы оптимизации. М.: Наука, 1977.
2.Бахвалов Н.С. Численные методы (анализ, алгебра, обыкновенные дифференциальные уравнения). М.: Наука, 1975.
3.Бородакий Ю.В., Крицына Н.А., Кулябичев Ю.П., Шумилов Ю.Ю.
Вероятностно – статистические методы обработки данных в информационных системах. М.: Радио и связь, – 2003.
4.Бородакий Ю.В., Лободинский Ю.Г. Основы теории систем управ-
ления (исследование и проектирование). М.: Радио и связь, – 2004.
5.Бородакий Ю.В., Муравьев С.К., Шумилов Ю.Ю. Нейросетевые ме-
тоды оптимальной кластеризации воздушных объектов. Труды ХIII Меж-
дународного научно-технического семинара “Современные технологии в задачах управления, автоматики и обработки информации”, Алушта, 2004.
ч.II.с. 216-218.
6.Васильев Ф.П. Численные методы решения экстремальных задач.
М.: Наука, 1988.
7.Вентцель Е.С. Исследование операций: Задачи, принципы, методо-
логия. М.: Высшая школа, 2001.
8.Вентцель Е.С. Теория вероятностей. М.: Высшая школа. 1999.
9.Владимиров В.И. Практические задачи по эксплуатации ядерных реакторов. М.: Атомиздат, 1976.
10.Доллежаль Н.А., Емельянов И.Я. Канальный ядерный энергетический реактор. М.: Атомиздат, 1980.
11.Дюран Б., Оделл П. Кластерный анализ. М.: Статистика, 1977.
12.Жемчугов В.П. и др. Методическое обеспечение аппаратуры кон-
троля герметичности оболочек (АКГО) твэл РБМК. ВАНТ. Серия: Техническая физика и автоматизация. Вып.59.ч. 2. 2005.С.18-25.
13.Загребаев А.М., Наумов В.И. О минимизации потери энерговыработки системы реакторов, работающих в переменном графике нагрузки //
Атомная энергия, 1979. Т.47. Вып.3. С.165-166.
14.Зангвилл У.И. Нелинейное программирование. Единый подход. М.: Советское радио,1973.
15.Зимин Г.В., Бурмистров С.К., Букин Б.М. Справочник офицера ПВО. М.: Воениздат, 1987.
16.Золотов В.П. и др. Общие принципы исследования эффективности боевых действий и вооружения: Тексты лекций. М.: ВАД, 1978 – 80с.
17.Иванов Н.М., Лысенко Л.Н. Баллистика и навигация космических аппаратов. М.: Дрофа, 2004.
18.Инвестиции / Под ред. В. Ковалевой, В. Ивановой. М.: Проспект,
2004.
19.Интрилигатор М. Математические методы оптимизации и экономическая теория. М.: Прогресс, 1975.
20.Калиткин Н.Н. Численные методы. М.: Наука, 1978.
241
21.Канторович Л.В, Горстко А.Б. Математическое оптимальное программирование в экономике. М.: Знание, 1968.
22.Карманов В.Г. Математическое программирование. М.: Наука,
1986.
23.Краюшкин А.В., Новиков В.Г., Федосов А.М. Экономический эф-
фект от использования уран-эрбиевого топлива в РБМК. // Материалы
научно-практическом семинара “Опыт эксплуатации, совершенствование и повышение эксплуатационной надежности ядерного топлива РБМК. Состояние и перспективы”. Электросталь, 23-25 апреля 2003. С.31-37.
24.Крянев А. Основы финансового анализа и портфельного инвестирования в рыночной экономике. М.: МИФИ, 2001.
25.Кулябичев Ю.П., Анитова Т.В. Теоретико-игровые методы исследо-
вания сложных систем. М.: МИФИ, 1994.
26.Кулябичев Ю.П., Крицына Н.А. Лабораторный практикум «Теоре- тико-игровые методы исследования сложных систем». М.: МИФИ, 1984.
27.Кулябичев Ю.П., Шляхов А.В., Шумилов Ю.Ю. Cравнительный ана-
лиз методов кластеризации. //Труды ХIII Международного научнотехнического семинара “Современные технологии в задачах управления, автоматики и обработки информации”, Алушта, 2003. С. 362-363.
28.Купалов-Ярополк А.И., Аден В.Г., Петров А.А. и др. Повышение эффективности использования топлива в РБМК-1000.// Атомная энергия, 2007.Т.103. Вып.1. С. 50-57.
29.Лесин В.В., Лисовец Ю.П. Основы методов оптимизации. М.:
МАИ, 1988.
30.Лисицын В. Основы методов оптимизации. М.: МАИ, 2003.
31.Максимов Ю.Я., Филипповская Е.А. Алгоритмы решения задач не-
линейного программирования. М.: МИФИ, 1982.
32.Медынский М.М. Численные методы нелинейной оптимизации (алгоритмы и программы): Учебное пособие. М.: МАИ, 2003.
33.Мещеряков Р.В., Шумилов Ю.Ю. Сравнительный анализ алгоритмов кластеризации.//Труды Х Международного научно-технического се-
минара “Современные технологии в задачах управления, автоматизации и обработки информации”, Алушта, 2001.
34.Муравьев С.К. Методика построения системы укрупнения и отображения воздушной обстановки. //Труды Х Международного научнотехнического семинара “Совеменные технологии в задачах управления, автоматизации и обработки информации”, Алушта, 2001. С. 247 – 248.
35.Новикова Н.М. Основы оптимизации (курс лекций). М., 1998. (www.ccas/ru).
36.Оуэн Г. Теория игр. М.: Мир 1973.
37.Пантелеев А.В. Методы оптимизации в примерах и задачах: учебное пособие для студентов высших технических учебных заведений. М.:
Высшая школа, 2005.
38.Пападимитриу Х., Стайглиц К. Комбинаторная оптимизация. М.:
Мир, 1985.
242
39.Партхасаратхи Т., Рагхаван Т. Некоторые вопросы теории игр двух лиц. М.: Мир, 1974.
40.Понтрягин Л.С. Обыкновенные дифференциальные уравнения. М.: Высшая школа, 1974.
41.Пугачев В.С. Теория вероятностей и математическая статистика.
М.: Наука, 1979.
42.Пшеничный Б.Н., Дажилин Ю.М. Численные методы в экстремальных задачах. М.: Наука, 1975.
43.Решетнев М.Ф., Лебедев А.А., Бартенев В.А. и др. Управление и навигация искусственных спутников Земли на околокруговых орбитах.
М.: Машиностроение, 1988.
44.Салмин И.Д. Математические методы решения оптимизационных задач: учебное пособие. М.: МИФИ, 2004.
45.Саати Т. Целочисленные методы оптимизации и связанные с ними
экстремальные проблемы. М.: Мир, 1973.
46.Санитарные правила проектирования и эксплуатации атомных станций (СП АС-03), СанПин 2.6.1.24-03, Минздрав России, Москва, 2003.
47.Сигал И.Х. Введение в прикладное дискретное программирование.
М.: Наука, 2007.
48.Струченков В.И. Математическое программирование: Методы, задачи, обучающие компьютерные программы: Учебное пособие. М.: МИ-
ФИ, 2004.
49.Субботин М.Ф. Введение в теоретическую астрономию. М.: Наука,
1968.
50.Техническая кибернетика. Книга 3. ч.1. /Под ред. Солодовникова В.В., М.: Машиностроение, 1986.
51.Таха, Хэмди. Введение в исследование операций. М.: Вильямс,
2001.
52.Ферапонтов М.М., Крицына Н.А., Деев Д.Л. Моделирование слу-
чайных воздействий на ЭВМ. М.: МИФИ, 1995.
53.Фокс А., Пратт М. Вычислительная геометрия. Применение в проектировании и на производстве. М.: Мир, 1982.
54.Хемминг Р.В. Численные методы: Пер. с англ. М.: Наука, 1972.
55.Цлаф Л.Я. Вариационное исчисление и интегральные уравнения.
М.: Наука, 1970
56.Эйкхофф В. Основы идентификации систем управления. М.: Наука,
1985.
57.Эльясберг П.Е. Определение движения по результатам измерений.
М.: Наука, 1976.
58.Энциклопедия финансового риск-менеджмента. Под ред. Лобанова А., Чугунова А. М.: Альпина Паблишер, 2003.
59.Lemke C.E., Howson J.J. Equilibrium points of bimatrix games // J. of the Society for Industrial and Mathematics. 1964. V. 12. P. 413 – 423.
60.Пантелеева А.В., Летовой Т.А. Методы оптимизации в примерах и задачах М.: Высшая школа, 2008.
243
НЕЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ В СОВРЕМЕННЫХ ЗАДАЧАХ ОПТИМИЗАЦИИ
Учебное пособие
Редактор Н.Е. Кочубей
Подписано в печать 15.11.2011. |
Формат 60×84 1/16 |
Печ. л. 15,25. Уч.-изд. л. 15,25. |
Тираж 100 экз. |
Изд. № 4/10. |
Заказ № 84. |
Национальный исследовательский ядерный университет «МИФИ». 115409, Москва, Каширское ш., 31
ООО «Полиграфический комплекс «Курчатовский». 144000, Московская область, г. Электросталь, ул. Красная, д.42
