
Варламов Линейные електрические цепи переменного тока Ч3. 2012
.pdfМИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ ЯДЕРНЫЙ УНИВЕРСИТЕТ «МИФИ»
Н. В. Варламов, А. Н. Филатов, Э. Я. Школьников
ЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПЕРЕМЕННОГО ТОКА
Часть III
Рекомендовано УМО «Ядерные физика итехнологии» в качестве учебного пособия
для студентов высших учебных заведений
Москва 2012
УДК 621.3 ББК 31.211 В18
Варламов Н.В., Филатов А.Н., Школьников Э.Я. Линейные электри-
ческие цепи переменного тока. Часть III: Учебное пособие. М.: НИЯУ МИФИ, 2012. – 60 с.
Пособие является логическим продолжением ранее изданных учебных пособий «Линейные электрические цепи переменного тока» (часть I, издание 2004 г. и часть II, издание 2008 г.).
В пособии рассматриваются линейные электрические цепи с распределенными параметрами при гармоническом внешнем воздействии. Во второй и третьей главах кратко изложены операторный метод расчета переходных процессов и метод расчета переходных процессов с помощью интеграла Дюамеля. Каждая глава сопровождается примерами решения типовых задач.
Пособие предназначено для студентов, обучающихся на факультете «Автоматика и электроника». Оно будет полезно также студентам других факультетов, изучающим курс «Электротехника».
Пособие подготовлено в рамках Программы создания и развития НИЯУ МИФИ.
Рецензенты: доктор физ.-мат. наук ОЯФА ФИАН А.В. Агафонов, канд. тех. наук, доц. МГТУ МИРЭА В.О. Вальтнер
ISBN 978-5-7262-1633-1 © Национальный исследовательский ядерный университет «МИФИ», 2012
CОДЕРЖАНИЕ |
|
Предисловие................................................................................................... |
4 |
Глава 1. Цепь с распределенными параметрами |
|
при гармоническом внешнем воздействии ........................................ |
5 |
1.1. Первичные параметры линии ....................................................... |
5 |
1.2. Дифференциальные уравнения |
|
однородной длинной линии ........................................................... |
6 |
1.3. Решение телеграфных уравнений |
|
для гармонического режима .......................................................... |
8 |
1.4. Прямые и обратные волны в длинной линии ............................. |
10 |
1.5. Уравнения передачи длинной линии |
|
(длинная линия как четырехполюсник) ....................................... |
14 |
1.6. Линии без потерь........................................................................... |
16 |
1.7. Входное сопротивление линии без потерь.................................. |
24 |
1.8. Согласование с помощью длинных линий без потерь............... |
27 |
Примеры................................................................................................ |
31 |
Глава 2. Операторный метод расчета переходных процессов ................ |
36 |
2.1. О некоторых ограничениях классического метода |
|
расчета переходных процессов ................................................... |
36 |
2.2. Об использовании свойств преобразования Лапласа |
|
для расчета переходных процессов............................................. |
37 |
Примеры................................................................................................ |
42 |
Глава 3. Расчет переходных процессов в линейных электрических |
|
цепях с помощью интеграла Дюамеля................................................ |
54 |
3.1 Временные характеристики линейных цепей ............................ |
54 |
Примеры................................................................................................ |
58 |
Список литературы....................................................................................... |
60 |
3
Предисловие
В первой главе учебного пособия рассматриваются линейные электрические цепи с распределенными параметрами при гармоническом внешнем воздействии. Во второй и третьей главах кратко изложены операторный метод расчета переходных процессов и метод расчета переходных процессов с помощью интеграла Дюамеля.
Для линейных электрических цепей с распределенными параметрами рассмотрены: первичные параметры линии, дифференциальные уравнения однородной длинной линии, решение телеграфных уравнений для гармонического режима, прямые и обратные волны в длинной линии, уравнения передачи длинной линии, особенности линии без потерь и вопросы согласования.
Изложение операторного метода расчета переходных процессов ограничено рассмотрением лишь тех свойств преобразования Лапласа, которые используются при построении простейших операторных схем замещения.
Для формирования первичного навыка решения типовых задач в каждой главе пособия приведены примеры, которые не только позволяют освоить простейшие практические приёмы, но во многих случаях дополняют содержание теоретических разделов.
Первая глава пособия подготовлена профессором Э.Я. Школьниковым, вторая – доцентом Н.В. Варламовым, третья – доцентом А.Н. Филатовым.
4
Глава 1. ЦЕПЬ С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ ПРИ ГАРМОНИЧЕСКОМ ВНЕШНЕМ ВОЗДЕЙСТВИИ
1.1.Первичные параметры линии
Втехнике связи по проводам передатчик и приемник соединены друг с другом парой проводов, образующих линию связи той или иной конструкции. Таким образом, линия связи является направляющей системой, вдоль которой распространяется электромагнитная энергия от передатчика (источника) к приемнику (нагрузка).
Как и всякая электромагнитная система, в которой протекают электрические токи и существуют электрические напряжения, линия связи обладает следующими параметрами: индуктивностью L, емкостью C, сопротивлением R и проводимостью G. При этом L определяется магнитным потоком, который сцеплен с контуром тока, образуемым токоведущими проводниками, а С определяется емкостью между проводниками и емкостью этих проводов по отношению к земле и к другим соседним проводам. Продольное активное сопротивление R определяется тепловыми потерями в проводах с учетом скин-эффекта и эффекта близости. Поперечная активная проводимость G определяется несовершенством изоляции, т.е. утечкой энергии.
На практике обычно рассматривают значения L, C, R, G, нормированные на длину линии, т.е. значения L, C, R, G линии еди-
ничной длины. Эти величины обозначаются через L0, C0, R0, G0 и называются первичными параметрами линии. Естественно, первичные параметры линии определяются конкретной геометрией линии и могут быть найдены либо экспериментально, либо теоретически с использованием методов теории поля.
Нетрудно видеть, что первичные параметры L0, C0, R0, G0 как бы распределены по линии, т.е. любой участоклинии, даже бесконечно малой длины, обладает этими параметрами. По этой причине подобные линии получили название «цепи с распределенными параметрами» или «длинные линии».
Вдальнейшем будут рассматриваться лишь такие линии, в ко-
торых первичные параметры L0, C0, R0, G0 не зависят от длины. Такие линии получили название однородных.
5
Для расчета токов и напряжений в длинных линиях нельзя применить классический аппарат электрических цепей с сосредоточенными параметрами. Это связано со следующими обстоятельствами.
Как известно, электромагнитная энергия распространяется с конечной скоростью, которая не может превышать скорость света. Конечная же скорость распространения энергии обуславливает волновой характер процесса. Это означает, что в цепях с распределенными параметрами процесс распространения электромагнитной энергии и распределение токов и напряжений является функцией не только времени, но и пространственных координат. В отличие от этого, в цепях с сосредоточенными параметрами независимо от пространственного расположения их элементов электромагнитные возмущения, т.е. токи и напряжения воспринимаются всеми элементами цепи практически в одно и то же время.
В этой связи для расчета токов и напряжений в длинных линиях необходимо, прежде всего, составить соответствующие уравнения, описывающие пространственно-временного распределения этих величин. Отметим, что ниже будет рассмотрена только одномерная по пространству задача, т.е. в качестве неизвестных будут рассматриваться напряжения u(x,t) и токи i(x,t), зависящие только от одной пространственной координаты х и времени t.
1.2.Дифференциальные уравнения однородной длинной линии
Рассмотрим элементарный участок однородной линии с распределенными параметрами длиной х, находящейся на расстоянии х от начала линии (рис. 1.1).
Здесь введены следующие обозначения:
u, i – напряжение и ток на входе в элементарный участок линии соответственно;
u+ u, i+ i – напряжение и ток на выходе элементарного участка линии соответственно;
L0 x, C0 x, R0 x, G0 x – полные индуктивность, емкость, сопротивление и проводимость данного участка линии.
6
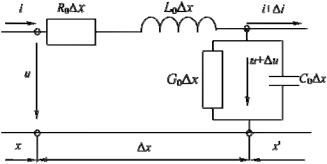
Рис. 1.1
В соответствии со вторым законом Кирхгофа:
u = R i x + L ∂i |
x +u + u |
|
0 |
0 ∂t |
|
или
−u = R0i + L0 ∂∂i x.
t
Всоответствии с первым законом Кирхгофа:
i =(u + u)G x +C |
|
∂(u + u) |
|
x +i + i |
|||||
0 |
|
|
|
|
|||||
|
|
0 |
|
∂t |
|
|
|||
или |
|
|
|
|
|
|
|||
|
G (u+Δu)+C |
∂(u+Δu) |
|
|
|
||||
− |
i = |
|
x. |
||||||
|
|
||||||||
|
|
0 |
0 |
|
|
||||
|
|
|
|
|
∂t |
|
|
||
(1.1)
(1.2)
Разделив обе части (1.1) и (1.2) на х, переходя к пределу при х→0 и пренебрегая членами более чем первого порядка малости, получим:
|
−∂u |
= R i + L ∂i ; |
|
|||||
|
|
∂x |
0 |
0 |
∂t |
(1.3) |
||
|
|
|
|
|
||||
− |
∂i |
|
=G u +C |
|
∂u . |
|
||
|
|
|
||||||
|
|
∂x |
0 |
|
0 |
∂t |
|
|
|
|
|
|
|
|
|||
Система уравнений (1.3) образует искомую систему уравнений для расчета u(x,t) и i(x,t) в длинных линиях. В литературе эти уравнения известны под названием телеграфных уравнений. Совместное решение телеграфных уравнений при заданных начальных и
7

граничных условиях позволяет в каждом конкретном случае решить поставленную задачу по определению u(x,t) и i(x,t).
Если за начало отсчета принять конец линии, т.е. ввести координату x' (рис. 1.11), то уравнения примут вид
∂u |
= R i + L ∂i , |
|||||
|
∂x' |
0 |
0 |
∂t |
||
|
|
|
|
|||
|
∂i |
=G u +C |
|
∂u . |
||
|
|
|
||||
|
∂x' |
0 |
|
0 |
∂t |
|
|
|
|
|
|||
Несмотря на внешнюю простоту телеграфных уравнений их решение для произвольных сопротивлений генератора и нагрузки и сигнала произвольной формы представляет собой сложную, хотя и принципиально разрешимую задачу.
Ниже будут рассматриваться случаи установившегося режима гармонических колебаний в линии.
1.3.Решение телеграфных уравнений для гармонического режима
Пусть напряжение и ток в линии изменяются гармонически со временем. Тогда эти величины могут быть представлены в следующем виде:
u(x,t) = Im |
|
|
(x)e |
jωt |
, |
i(x,t) = Im |
|
|
jωt |
, |
U |
|
|
I (x)e |
|
||||||
|
|
|
|
|
|
|
|
|||
где U (x) и I (x) – комплексные амплитуды напряжения и тока,
зависящие от продольной координаты.
Используя метод комплексных амплитуд, преобразуем телеграфные уравнения (1.3):
|
|
|
|
|
|||
− |
dU |
=(R0 + jωL0 ) I; |
|||||
dx |
|||||||
|
|
|
(1.4) |
||||
|
|
|
|
|
|||
− |
dI |
=(G |
+ jωC |
)U. |
|||
|
|||||||
|
dx |
0 |
0 |
|
|||
|
|
|
|
||||
Исключим из этих уравнений величину İ, для чего продифференцируем первое уравнение системы (1.4) и подставим в него зна-
чение dI из второго уравнения. Тогда dx
8
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
d U |
|
=(R + jωL )(G + jωC )U. |
(1.5) |
|||||||||||||
|
dx2 |
||||||||||||||||
|
|
|
0 |
|
|
|
|
|
0 |
0 |
0 |
|
|||||
Аналогично, исключая из (1.4) величину U , получим уравне- |
|||||||||||||||||
ние относительно İ: |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
d |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
I |
=(R |
+ jωL |
)(G + jωC ) I. |
(1.6) |
|||||||||||
|
|
|
|
|
|||||||||||||
|
|
dx2 |
|
|
|
|
0 |
|
|
0 |
0 |
0 |
|
||||
Обозначим γ = (R0 + jωL0 )(G0 + jωC0 ) |
и перепишем уравне- |
||||||||||||||||
ние (1.5) и (1.6) в виде |
d 2U |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
2 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
2 |
|
− γ |
U = 0; |
|
|
||||
|
|
|
|
dx |
|
|
|
|
|
|
|
|
(1.7) |
||||
|
|
|
|
|
|
d |
2 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
I |
− γ |
2 |
I = 0. |
|
|
||||
|
|
|
|
|
|
dx |
2 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Общее решение первого уравнения системы имеет вид |
|
||||||||||||||||
|
U (x) = A e−γx |
+ A eγx , |
|
(1.8) |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
2 |
|
|
|
где постоянные интегрирования А1 и А2 определяются граничными условиями.
Ток İ получается подстановкой (1.8) в первое уравнение систе-
мы (1.4): |
1 |
|
|
|
||
I (x) = |
(A1e−γx − A2eγx ), |
(1.9) |
||||
|
|
|||||
|
Zв |
|
||||
где |
|
|
|
|
|
|
Zв = |
|
R0 + jωL0 |
. |
(1.10) |
||
|
|
|||||
|
|
G0 + jωC0 |
|
|||
Постоянные γ и Zв найденного общего решения получили название соответственно коэффициента распространения и волнового сопротивления. Как γ, так и Zв являются комплексными величинами, которые можно представить в следующей форме:
γ = (R0 + jωL0 )(G0 + jωC0 ) = α+ jβ, |
|
|||||||
Zв = |
R0 + jωL0 |
= |
|
Zв |
|
e jϕв . |
(1.11) |
|
|
|
|||||||
|
||||||||
|
G0 + jωC0 |
|
|
|
|
|
||
9

Вещественную часть α коэффициента распространения γ называют коэффициентом затухания, а мнимую часть β – коэффициентом фазы.
Коэффициенты распространения γ, затухания α, фазы β и волновое сопротивление линии Zв относятся к числу так называемых волновых или вторичных параметров линии. Волновые параметры зависят от значения первичных параметров линии и являются функциями частоты. Смысл этих коэффициентов будет рассмотрен ниже.
1.4. Прямые и обратные волны в длинной линии
Используя (1.8)–(1.11), а также связь u(x,t) и i(x,t) с комплексными амплитудами, перейдем к мгновенным значениям u(x,t) и i(x,t):
u(x,t) = |
|
|
|
|
|
A |
|
e−αx sin(ωt −βx + ϕ ) + |
|
||||||||
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
+ |
|
|
|
|
A |
|
eαx sin(ωt +βx + ϕ |
2 |
), |
|
|||||||
|
|
|
|||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|||||
i(x,t) = |
|
|
A1 |
|
|
|
e−αx sin(ωt −βx +ϕ1 −ϕв ) − |
(1.12) |
|||||||||
|
|
|
|||||||||||||||
|
|
|
|||||||||||||||
|
|
|
|
Zв |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
−A2 eαx sin(ωt +βx + ϕ2 −ϕв),
Zв
где φ1 и φ2 аргументы комплексных величин А1 и А2, а φв – аргумент волнового сопротивления.
Как явствует из (1.12), каждое из решений представляет собой сумму двух слагаемых. Рассмотрим сначала первые из них:
uпр (x,t) = |
|
|
|
|
A1 |
|
e−αx sin(ωt −βx +ϕ1 ); |
|
|
||||||||
|
|
|
|||||||||||||||
|
|
|
|
A1 |
|
|
|
|
|
|
|
|
|
|
(1.13) |
||
iпр (x,t) = |
|
|
|
|
|
|
e |
−αx |
sin(ωt −βx +ϕ1 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
−ϕв ). |
|
||||
|
|
|
Zв |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Анализ (1.13) показывает, что они могут быть интерпретированы как бегущие волны соответственно напряжения и тока, распространяющиеся вдоль положительного направления оси х с коэффициентом затухания α. Эти бегущие волны получили название прямых (или падающих) волн напряжения и тока.
10
