Переход от параметрических к непараметрическим моделям безотказности

Формулы, приведенные в табл. 1, позволяют вычислить ве­роятность безотказной работы при однократном приложении на­грузки. В реальных условиях эксплуатации конструкции нагру­жаются многократно, причем наиболее характерны случайные циклы нагружения.

По степени неопределенности прочность и нагрузка могут быть отнесены к одной из трех категорий:

1)детерминированным величинам — принимают известные за­ранее значения, могут служить приемлемой аппроксимацией полностью контролируемых процессов;

2)фиксированным случайным величинам — они случайны в на­чальный момент времени, а далее изменяются во времени извест­ным образом. Например, это может быть функция или ,где k - число циклов нагружения;

3)независимым случайным величинам — последовательные зна­чения, принимаемые ими во времени, статистически независимы. Обычно последовательные значения нагрузки независимы, а прочность может изменяться случайным образом и быть незави­симой от цикла к циклу нагружения только в том случае, если на нее влияют другие факторы окружающей среды, независимые от процесса приложения нагрузки (температура, вибрация и пр.);

Прочность зависит от числа циклов приложения нагрузки, ее величины и продолжительности. Эффект изменения прочности во времени называется старением, или износом. В табл. 3 приве­дены выражения вероятности безотказной работы при много­кратных случайных циклах нагружения .

Таблица 3 - Выражения вероятности безотказной работы при многократных случайных циклах нагружения Характер изменения прочности	Характер изменения нагрузки	Вероятность безотказной работы после N циклов на­гружения
Детерминированная невозрастающая ве­личина	Детерминированная неубывающая вели­чина
Фиксированная слу­чайная величина	Детерминированная постоянная величина
Независимая случай­ная величина	Детерминированная постоянная величина
Детерминированная постоянная величина	Фиксированная слу­чайная величина
Фиксированная слу­чайная величина	Фиксированная слу­чайная величина
Независимая случай­ная величина	Фиксированная слу­чайная величина
Детерминированная величина	Независимая случай­ная величина
Фиксированная слу­чайная величина	Независимая случай­ная величина

Примечание. В таблице - вероятность безотказной работы при еди­ничном нагружении. Независимая случай­ная величина

Независимая случай­ная величина

Анализируя формулы, приведенные в табл. 3 для ряда прак­тически важных частных случаев, приходим к широко распро­страненной непараметрической экспоненциальной модели изме­нения вероятности безотказной работы во времени:

.

Определим основные понятия полученной модели. Отказ яв­ляется случайным событием, следовательно, время от момента включения устройства до первого отказа (наработка) тоже слу­чайная величина т. Вероятность безотказной работы определяется условием , т. е. вероятностью того, что наработка до первого отказа превышает t. В интервале от 1 до 0 функция R (t) — монотонно убывающая.

Вероятность того, что отказ произойдет через время t после включения, определяется условием . Плот­ность вероятности момента первого отказа

откуда .

Средняя наработка до отказа (или среднее время безотказной ра­боты) вычисляются по формуле

или .

Интенсивность отказов = f(t)/R(t), откуда

При постоянной интенсивности отказов = const имеем R(t) = ехр{- t}, т. е. получаем экспоненциальное распределение времени безотказной работы

Математическое ожидание этого распределения , дисперсия . Экспоненциальное распределение являет­ся фундаментальным распределением в теории надежности: ос­новные результаты получены в предположении адекватности этого распределения реальным процессам возникновения отказов.

Структурные методы - резервирование

Пуассоновский процесс возникновения отказов

Разработанные в теории надежности различные методы ре­зервирования преследуют одну основную цель - создание на­дежных систем из ненадежных элементов. Наиболее общим ме­тодом расчета безотказности систем с различными видами ре­зервирования (параллельное соединение элементов - горячий резерв, включение резервного оборудования замещением - хо­лодный резерв, различные схемы голосования) является метод, основанный на использовании марковских процессов, или мар­ковских цепей.

Предположим, что имеется п одинаковых образцов оборудо­вания, причем в любой момент времени неисправностям под­вержен только один образец. Состояние системы будет опреде­ляться числом отказавших образцов. Так, в состоянии 0 все п образцов исправны, а в состоянии п - нет ни одного исправного образца. Нас интересует вероятность отказа точно образцов оборудования (к < п) к моменту времени /. Приняв, что в на­чальный момент t = 0 система находится в состоянии 0 (т. е. в этот момент все образцы исправны), будем одновременно пола­гать, что:

а) вероятность перехода в интервале равна

б) вероятность появления более одного отказа в интервале равна 0 ( );

в) вероятности переходов не зависят от состояния системы.

Используя эти допущения, можно составить матрицу перехо­дов Р, которая описывает процесс в интервале . Например, если в момент t система находится в состоянии 0, то условная ве­роятность остаться в этом состоянии в момент равна . Вероятность перехода в состояние 1 равна , а вероятность пе­рехода в состояние с номером больше 1 равна 0 ( ) на основании предположения б). Аналогично, если система находится в состоя­нии 1 в момент t, то она останется в этом состоянии в течение с вероятностью или перейдет в состояние 2 с вероятно­стью .

Заметим, что данная система не может вернуться в состояние О, если не производятся ремонты отказавших образцов. Соответ­ственно, если ремонты не производятся, то система, находившая­ся в состоянии п в момент времени t (все п образцов неисправны), будет, очевидно, оставаться в этом состоянии в интервале . Учитывая каждое из этих условий, можно составить матрицу пе­реходов. Следует заметить, что сумма элементов каждой строки матрицы Р равна 1, так как система должна находиться в одном из п состояний. Такие матрицы называются стохастическими. Если сумма элементов каждой строки и каждого столбца равна 1, то та­кая матрица называется дважды стохастической:

Здесь, как и далее, в матрицах вероятностей переходов Р для краткости опущено .

Подобная формулировка непосредственно приводит к системе линейных однородных дифференциальных уравнений с постоян­ными коэффициентами. Решение этой системы можно найти ли­бо с помощью матричных методов, либо непосредственно из дифференциальных уравнений. Для системы, которая должна на­ходиться в состоянии 0 в момент , нужно, чтобы она была в этом состоянии в момент времени t и оставалась в нем в течение времени .

Таким образом, пребывание в состоянии 0 является слож­ным событием, состоящим из события первоначального пребы­вания системы в состоянии 0 и отсутствия переходов из этого состояния. Следует отметить, что элементы столбцов матрицы переходов, соответствующие каждому состоянию, редставляют собой коэффициенты при для вероятностей отсутствия пере­ходов из этих состояний за интервал . Поэтому можно непосредственно записать вероятности пребывания в каждом состоянии:

,

,

.

Представим, например, в виде

.

На основании определения производной и из условия получим .

Аналогично находим остальные уравнения:

Если предположить, что при t = 0 все образцы оборудования исправны, то начальные условия .

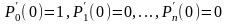Теперь нужно решить эту систему дифференциальных урав­нений, что позволит определить вероятность появления точно к отказов к моменту времени t. Введем преобразование Лап­ласа, которое позволяет перейти от системы дифференциальных уравнений к системе алгебраических уравнений. Пусть

и

Найдем сначала . Применяя преобразование Лапласа к первому уравнению системы, получим и

Используя обратное преобразование Лапласа, находим

.

Таким образом, вероятность отсутствия отказов к моменту времени t является экспоненциальной функцией времени. С по­мощью относительно легко найти и т.д. Так, .

После применения преобразования Лапласа это уравнение приобретает следующий вид:

,

откуда

и .

Действуя тем же способом, находим, что (к= 0, 1, 2,..., n-1), откуда

что представляет собой выражение вероятности появления точно к отказов согласно распределению Пуассона.

Распределение получают суммированием этих вероятностей. Поэтому вероятность появления самое большее к (к < п) отказов за время t

Интересно отметить, что пуассоновский процесс приводит не­посредственно к другому распределению, известному под названием гамма-распределения. Для распределения Пуассона случайной вели­чиной является число отказов, а для гамма-распределения - время. Функцию плотности вероятности для гамма-распределения пред­ставим в терминах преобразования Лапласа как . Применяя обратное преобразование к , получим

.

Тот же результат получается при рассмотрении суммы независи­мых случайных величин, имеющих экспоненциальное распределение.

Включение резервного оборудования замещением

В данной схеме включения п одинаковых образцов оборудо­вания только один находится все время в работе (рис. 2). Когда работающий образец выходит из строя, его непременно отключают, и в работу вступает один из (n - 1) резервных (запасных) образцов.

Этот процесс продолжается до тех пор, пока все (п - 1) резервных, или запасных,

о бразцов не будут исчер­паны.

Рисунок 2. Схема включения оборудования замещения

Примем для этой системы следующие допущения:

1. Отказ системы происходит, когда откажут все п образцов.

2. Вероятность отказа каждого образца оборудования не зависит от состояния остальных (п - 1) образцов оборудования.

3. Отказывать может только оборудование, находящееся в ра­боте, и условная вероятность отказа в интервале t,t+dt равна dt; запасное оборудование не может выходить из строя до того, как оно будет включено в работу.

4. Переключающие устройства считаются абсолютно надеж­ными.

Процесс появления отказов в такой схеме включения является непосредственным следствием процесса. Система способна выполнять требуемые от нее функции, если исправен по крайней мере один из п образцов оборудования. Таким образом, в этом случае надежность равна просто сумме вероятностей состояний системы, исключая со­стояние отказа, т. е.

В качестве примера рассмотрим систему, состоящую из двух резервных образцов оборудования, включаемых замещением. Для того чтобы эта система работала в момент времени t, нужно, что­бы к моменту t были исправны либо оба образца, либо один из двух. Поэтому

Р исунок 3. Надежность системы при включении резерва замещения и при параллельной работе

На рис. 3 пока­зан график функции R(t) и для сравнения приведен аналогичный график для нерезерви­рованной системы. Во многих случаях нель­зя предполагать, что запасное оборудова­ние не выходит из строя, пока его не включат в работу.

Пусть - интен­сивность отказов ра­ботающих образцов,а - резервных, или запасных. В случае дублированной систе­мы имеем следующую матрицу переходов:

0 1 2

Поступая, как и раньше, получим для нее следующую систему дифференциальных уравнений:

с начальными условиями . Примене­ние преобразования Лапласа дает

Так как то необходимо обратным преобра­зованием определить оригиналы изображений P₀(s) и 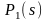. Мож­но также найти и , поскольку

,

Для определения используем разложение на простые дроби:

Коэффициенты А и В находим, решая следующие уравнения:

Отсюда и ,a потому

Окончательно функция надежности имеет вид

В некоторых случаях отказ системы возникает вследствие оп­ределенных комбинаций отказов образцов входящего в систему оборудования и (или) из-за внешних воздействий на эту систему. Рассмотрим, например, искусственный спутник с двумя радиопере­датчиками, один из которых является резервным, или запасным. Отказ системы (потеря связи со спутником) возникает при выхо­де из строя двух передатчиков или в тех случаях, когда солнечная активность создает непрерывные помехи радиосвязи. Если ин­тенсивность отказов работающего передатчика равна , а - ожидаемая интенсивность появления радиопомех, то матрица пе­реходов имеет следующий вид:

0 1 2

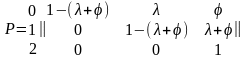
а функция надежности системы

Данный тип модели также применим в случаях, когда резерв по схеме замещения отсутствует. Например, предположим, что космический корабль подвергается бомбардировке микрометео­ритами, причем бомбардировка небольшими частицами происхо­дит с интенсивностью , а большими - с интенсивностью . Для выхода из строя космического корабля ему достаточно получить п малых повреждений или одно большое. Тогда матрица переходов Р имеет вид

0 1 2 ... n

Здесь состояние процесса представляется числом ударов или повреждений, причем встреча с большой частицей (метеоритом) равносильна п ударам малых частиц. Надежность, или вероят­ность того, что корабль не будет разрушен действием микроме­теоритов к моменту времени t, имеет вид: