
Лекция_3
.pdfЛекция 3. Символы Леви-Чивиты. Определитель и
векторное произведение
1. Символы Леви-Чивиты определяются следующим образом:
|
|
|
|
1, |
если перестановка |
|
123 |
|
|
||
|
|
|
|
|
|
четная, |
|
||||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
123 |
|
|
|
|
|
|
|
|
1, |
если перестановка |
нечетная, |
(56) |
||||
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
0, если хотя бы два из трех индексов одинаковы. |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример: 123 1, |
213 1, 231 1, 112 0. |
|
|
|
|
|
|
||||
2. Рассмотрим в качестве примера применения символов Леви-Чивиты
расчет определителя g метрического тензора G в трехмерном пространстве.
По определению
g det G sign g1i g2 j g3k . |
(57) |
S |
|
Здесь сумма берется по всем перестановкам из 123 в ijk . |
sign – знак |
перестановки. Но в силу определения (56) детерминант (57) можно переписать в следующем виде:
|
|
|
|
|
|
g ijk g |
g |
2 j |
g |
3k |
|
. |
(58) |
||||||||
|
|
|
|
|
|
|
|
|
1i |
|
|
|
|
|
|
|
|
||||
Нетрудно видеть из (58), что |
|
g A123 , где |
|
|
|
A123 – антисимметричный объект |
|||||||||||||||
(по всем индексам). В самом деле. |
Рассмотрим, например, |
A213 . По |
|||||||||||||||||||
определению, A |
ijk g |
2i |
g |
g |
3k |
jik g |
2 j |
g |
g |
3k |
|
. Но ijk jik . Следовательно, |
|||||||||
213 |
|
1 j |
|
|
|
|
1i |
|
|
|
|
|
|
|
|||||||
A123 A213 . Поэтому имеем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
Almn lmn A123 |
lmn g, |
(59) |
|||||||||||||||
|
|
|
|
|
A |
|
ijk g |
|
g |
|
|
|
g |
|
|
|
. |
||||
|
|
|
|
|
|
li |
mj |
nk |
|
||||||||||||
|
|
|
|
|
|
lmn |
|
|
|
|
|
|
|
||||||||
Таким образом, приходим к полезному соотношению:
|
lmn |
g ijk g |
li |
g |
mj |
g |
nk |
. |
(60) |
|
|
|
|
|
|
Задание 9. Доказать справедливость следующего выражения для
определителя метрического тензора:
det G |
1 |
lmn ijk gli gmj gnk . |
(60.1) |
|
6 |
||||
|
|
|
3. Нетрудно проверить, что с использованием символов Леви-Чивиты векторное произведение в декартовой системе координат можно представить в виде:
a b a b e |
. |
(61) |
|
|
|
В самом деле. Найдем, например, проекцию векторного произведения на ось
Ox . Она имеет следующий вид:
a b x a b 1 1a b .
Приняв во внимание определение (56), распишем это выражение подробнее:
1a b 231a2b3 321a3b2 aybz azby .
Сравнив этот результат с (35), убеждаемся в том, что формула (61)
справедлива. С другой стороны, формула (61) представляет собой определитель, выраженный через символы Леви-Чивиты, что и используется в алгебре. Заметим только, что в силу свойств символов Леви-Чивиты, (61)
можно переписать в виде
a b a b e . |
(61.1) |
|
|
Более того, так как справедливо равенство (50), векторное произведение можно переписать в виде:
a b |
|
a b e . |
(61.2) |
|
|
|
Следует особо отметить, что выше проведенные выкладки настоящей лекции справедливы в декартовой системе координат. Случай криволинейных координат мы рассмотрим ниже.
Задание 10. Убедится в справедливости выражений (61.1) и (61.2).
4. Рассмотрим теперь смешанное произведение. Для этого умножим скалярно вектор a b на вектор с :
a b ,c a b e c e |
a b c e e |
|
||||||||
|
|
|
|
|
ax |
ay |
az |
|
(62) |
|
|
|
|
|
|
|
|||||
a b c |
a b c |
|
b |
b |
|
b |
. |
|||
y |
|
|||||||||
|
|
|
|
|
x |
|
z |
|
|
|
|
|
|
|
|
cx |
cy |
cz |
|
|
|
Как известно из курса геометрии, это произведение представляет собой объем, построенный на векторах a , b и с .
Далее, очевидно, что ei i e и ei i e .
Задание 11. Убедитесь в этом.
В связи с этим нетрудно показать, что cмешанное произведение базисных векторов приводит к символу Леви-Чивиты. В самом деле,
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
i |
||
e |
i |
e |
|
,e |
|
|
|
|
|
ijk |
|
|
1 |
||||
|
|
j |
|
|
i |
j |
k |
|
|
|
|
j |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
Аналогично |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
||
ei |
e j |
,ek |
|
i |
j k |
ijk |
|
j |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
i2
j2
k2
2i
2j
2k
i3
3j .
k3
3i
3j .
3k
(63)
(64)
Учитывая (63) и (64), получим важную для конкретных расчетов формулу:
1i
ijk lmn 1j
1k
1i 2i
1j 2j1k 2k
2i
2j
2k
3i
3j
3k
3i
3j
3k
l1
l2
l3
l1
m1
n1
m1
m2
m3
2 |
3 |
|
l |
l |
|
2 |
3 |
|
m |
m |
|
2 |
3 |
|
n |
n |
(65) |
1 |
|
|
|
||
|
|
|
n |
|
|
2 |
. |
|
n |
|
|
3 |
|
|
n |
|
|
Перемножим определители, учитывая правило суммирования Эйнштейна и определение символов Кронекера. Например, перемножая первую строку первого определителя на первый столбец второго определителя, получим:
i 1 |
i 2 |
i 3 |
i |
i . |
|
1 l |
2 l |
3 l |
|
l |
l |
Следовательно, из (65) имеем важную формулу:

|
|
|
i |
i |
i |
|
|
|
|
|
|
|
|||
|
|
|
l |
m |
n |
|
|
ijk |
lmn |
|
j |
j |
j |
. |
(66) |
|
|
l |
m |
n |
|
|
|
|
|
|
k |
k |
k |
|
|
|
|
|
l |
m |
n |
|
|
|
|
|
|
|
|
|
|
Задание 12.
1. Показать, что
a.kij kmn mi nj mj ni ,
b.kij kin 2nj ,
c.kij ijk 6 ,
d.ijk klm mlq 2 jiq .
2.Записать в векторном виде
a.jkiaib j ak ,
b.ilm lknamak bibn ,
c.aibnck klmal nibm ,
d.ijk imn klp nqpa j amblcq .
3.Используя символы Леви-Чивиты, доказать тождество
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
b c b |
|
ac |
|
|
ab |
|
. |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4. Доказать тождества |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
ad |
|
|
|
||||||||||||||||
a. |
a b c d |
ac |
(тождество Лагранжа), |
||||||||||||||||||
|
|
|
|
bc |
bd |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
b. |
a b c |
b c a |
c a b 0 (тождество Якоби), |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
a1 b1 c1 a2 b2 c2 |
|
a1a2 |
a1b2 |
|
a1c2 |
|
|
|
||||||||||||
|
|
|
|
|
|
||||||||||||||||
c. |
|
b1a2 |
b1b2 |
|
b1c2 |
, |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
c1a2 |
c1b2 |
|
c1c2 |
|
|
|
||||
d.a b c d b c a d c a b d 0 ,
e.a b c d b a c d a b c d ,
(67)
(68)
(69)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 . |
|
|
|
||
|
f. |
|
|
a |
b |
|
b c |
|
|
|
c a |
|
a |
|
b c |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
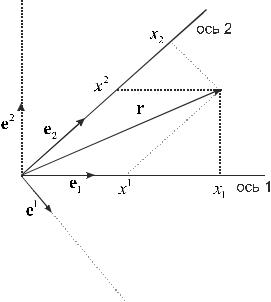
5. Косоугольная система координат. Обратная решетка. |
|||||||||||||||||||||||||
|
Наиболее наглядно разница |
|
между |
|
|
|
||||||||||||||||||||
ко- и контравариантными компонентами |
|
|
|
|||||||||||||||||||||||
видна на примере косоугольной системы |
|
|
|
|||||||||||||||||||||||
координат. Из соотношений (46) следует, |
|
|
|
|||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||
что e1 e2 |
|
и |
e1 e3 . |
|
Это |
|
значит, что, |
|
|
|
||||||||||||||||
e1 k e |
2 |
e |
3 |
. Но e1e |
1. Следовательно, |
|
|
|
||||||||||||||||||
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
k |
|
|
|
|
. |
|
Здесь |
V |
– |
|
|
объём, |
|
|
|
|||||||||||
e1, e2 |
e3 |
V |
|
|
|
|
|
|
||||||||||||||||||
построенный на базисных векторах. Таким |
|
|
|
|||||||||||||||||||||||
образом, |
базисный |
вектор |
e1 |
|
взаимной |
|
|
Рис. 8 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
системы координат можно представить в |
|
|
|
|||||||||||||||||||||||
виде |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
e2 e3 |
|
|
e2 e3 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e1, e2 e3 |
V |
||||||||||
|
Аналогично можно записать, что |
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e2 |
e3 e1 |
, |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e3 |
e1 e2 . |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V |
|
|
|
|
|
(70)
(71)
На рис. 8 показаны базисные векторы исходной косоугольной системы координат и базисные векторы взаимной системы координат. Ковариантные компоненты x радиус-вектора r , представленного на рис. 8, определяются как скалярные произведения r на базисные векторы e :
re x e |
|
|
(72) |
|
e x x . |
||
Т.е. ковариантные компоненты x |
– это проекции радиус-вектора на оси |
||
исходной системы координат. |
|
Контравариантные компоненты |
x |
представляют собой скалярные произведения r на базисные взаимные векторы e :
|
x |
|
|
x |
|
|
|
(73) |
re |
|
e e |
|
|
x . |
В физике твердого тела вводится понятие обратной решетки – периодической решётки в так называемом обратном пространстве, элементарные векторы
трансляции которой bk связаны с векторами трансляции ak |
исходной прямой |
решётки (решётки Браве) следующими условиями: |
|
ak bj 2 kj . |
(74) |
Как видно из вышеизложенного, обратная решетка – это решетка во взаимном базисе.
Задание 13.
1.Показать, что если две решетки являются обратными одна по отношению к другой, то произведение объемов их элементарных ячеек рано единице.
2.Выразить углы между векторами обратной решетки через углы прямой решетки.
