Лекция 7

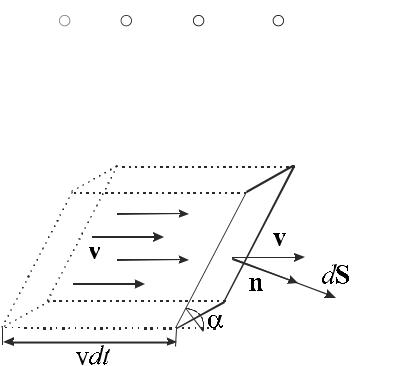
Лекция 7. Поток векторного поля и дивергенция.

Теорема Остроградского-Гаусса

1. Пусть в каждой точке пространства задана векторная функция a r .

Говорят, что задано векторное поле. Если векторное поле можно представить в виде градиента от некоторого скалярного поля, то такое поле называется потенциальным.

Потоком векторного поля a r через замкнутую поверхность S

называется следующая конструкция:

Разумеется, поток можно определить и через незамкнутую поверхность.

Пример. Сила тока определяется как заряд, прошедший через некоторую площадку в единицу времени I dq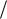dt .

Рис. 12. К определению плотности тока.

Пусть перемещаются частицы зарядом e каждая со скоростью v . Если dN –

число частиц, переместившихся за время dt , – число частиц в единице объема среды, то через малую площадку dS протекает заряд

dq edN e dV .

Объём dV , который занимают частицы, переместившиеся за время dt (см.

рис. 12) можно представить в виде:

dV dt vsin dS dtvdS.

Тогда

dq e dtvdS.

Полный заряд, прошедший через площадку S , равен

dq dt e vdS.

S

Сила тока, таким образом, принимает вид:

I e vdS.

S

Это и есть поток заряда через площадку S . Вектор j e v

называется плотностью тока или плотностью потока заряженных частиц. Т.е.

сила тока – это поток вектора j через площадку S :

I jdS jk dSk .

SS

2.Дивергенцией векторного поля a r в точке r – это предел

отношения потока векторного поля a r через замкнутую поверхность S ,

ограничивающую объем V , окружающий точку r , к этому объему при стремлении последнего к нулю:

Найдем удобное для расчетов выражение для дивергенции в декартовых

координатах. Для этого в качестве объема V выберем бесконечно малый

прямоугольный параллелепипед со сторонами dx , dy и dz . Поток

Вынося за скобку общий множитель dxdydz , получим:

Вспоминая определение оператора «набла» (133), представим дивергенцию (145) в виде скалярного произведения

Все производные берутся в точке, в которую стягивается объем V . Итак,

дивергенция векторного поля a r в точке r – это число, равное скалярному произведению оператора Гамильтона на вектор a r . В каждой точке пространства, таким образом, векторному полю можно сопоставить скалярное поле по правилу (146). Если при этом окажется, что везде diva 0 ,

то такое векторное поле называется соленоидальным или трубчатым.

Пример. Найти дивергенцию вектора a r , зависящего от модуля радиус-

вектора. Согласно (146) и правилу взятия сложной производной имеем:

Задание 24.

1.Найти векторные линии следующих полей:

a.E ar ,

b.E a ,

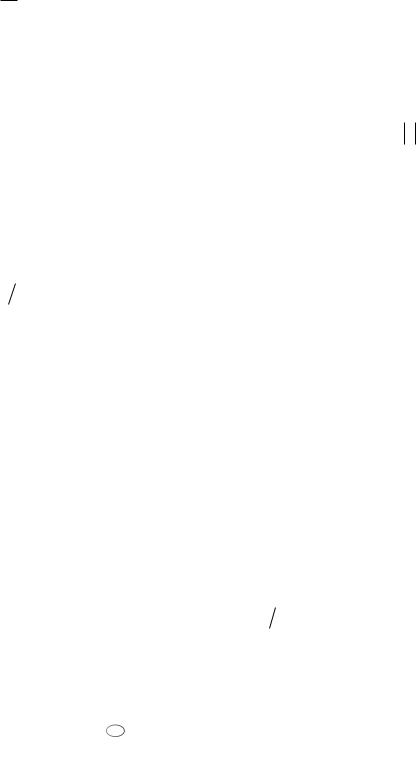
c.E a r ,

d.E rq3 r ,

e.E z y ex x z ey y x ez .

Указание: Векторной линией поля E называется линия, касательная

ккоторой в каждой точке совпадает с вектором E .

2.Найти дивергенцию векторного поля A . Если не сказано противного, считать, что a,b,d – постоянные векторы, k – константа, r r .

a.A r3r ,

b.A zr ,

c.A r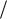r ,

d.A [a r] ,

широко применяемая в физике. Она гласит, что интеграл от дивергенции вектора a по объёму V равен потоку этого вектора через замкнутую поверхность S , ограничивающую объем V .

Пример. Докажем, что

В качестве примера применения полученного соотношения докажем тождество:

задана напряженность электрического поля E :

a.E x2 4sin z exp xy ,cos x ln xyz , xy2 z ,

b.E x exp x2 y z,ln xy sin z , x y z 1 .