Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Институт сферы обслуживания и предпринимательства ДГТУ

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

ОТЦ модули / М1_ОТЦ_1

.pdf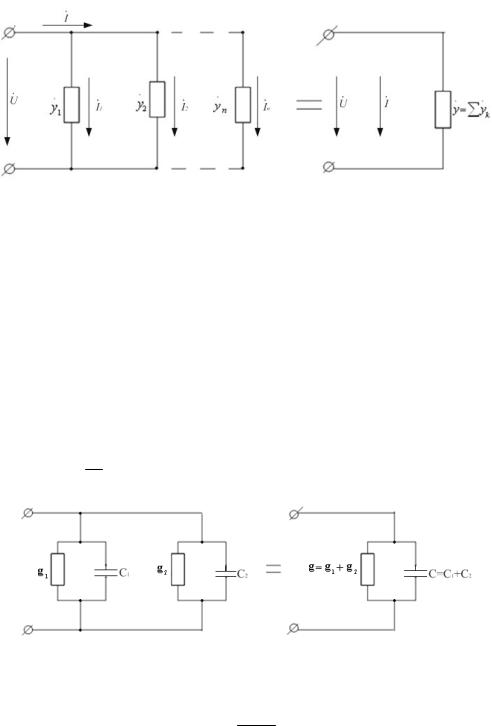

Скачиваний:

Добавлен:

09.02.2015

Размер:

1.29 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 56 / 96 7 8 9 > Следующая >>>

Рис. 3.4. К расчёту эквивалентной комплексной проводимости

. . .		.
I I1 I2 ... In,
. . . . .		. .
I Y1U Y2U ... YnU,
.	. n .	. .
I U Y k UY .
	k 1
. n .
Величина Y Yk	называется	эквивалентной комплексной
k 1

проводимостью. Если мнимые части представляют собой проводимости или

ёмкостного, или индуктивного характера, то Y находится в результате арифметического сложения отдельных активных проводимостей gk, ёмкостей

Сk или величин 1 (рис. 3.5).

Рис. 3.5. Преобразование параллельных ветвей цепи

Для цепи рисунка 3.6 величина активного сопротивления r будет равна:

r r1 r2 . r1 r2

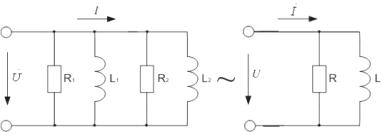
Рис. 3.6. Преобразование схемы, содержащей только сопротивления и индуктивности

Индуктивность L определяется из выражения:

							L			L1 L2			.
						.	L		L1 L2				.
									L1 L2

	Найдём проводимость Y эквивалентной схемы:
.	1	1	r r		L L			1	1			1			1	1					1	1	).
Y			1	2	1 2		(				)			(			) g	g	2	j(
Y							(				)			(			) g	g		j(
	r	j L	r1 r2		jL1 L2 r1					r2		j L1				L2	1				L1	L2
	r	j L	r1 r2		jL1 L2 r1					r2		j L1				L2					L1	L2

Для цепей, содержащих n ветвей, которые состоят только из активных сопротивлений и индуктивностей, активная и реактивная составляющие

проводимости Y определяются выражениями:

n				n
gRC gk ,	bRC Ck ,
k 1		1		k 1	1
n				n
gRL gk ,	bRL					.

k 1			k 1		Lk

Отношение токов в ветвях таких цепей прямо пропорционально отношению их комплексных проводимостей. Поэтому ток в k-й ветви равен произведению суммарного тока всех ветвей на отношение её комплексной проводимости к проводимости всей цепи:

			.		.
.		.	Y	.	Z
I		I	k	I		.
I	k	I	.	I	.	.
	k		.		.

Y Zk

Для схем с двумя ветвями получим:

			.				.
			.				Z
.	.		Z 2	.	.		Z	1 .
I1 I				,I 2 I
I1 I		.	.	,I 2 I		.		.
		Z1 Z 2				Z1 Z 2

Рассмотрим комплексное сопротивление участка цепи

.		1
Комплексная проводимость Y				g jb, где:
Комплексная проводимость Y			.	g jb, где:
			Z
g			r		и b	x	.
	r	2 x2				r2 x2

Z r jx.

(3.1)

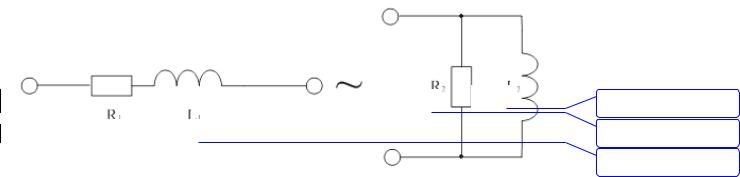
Если два элемента с проводимостями g и b, вычисленными по формулам (3.1), соединить параллельно, то суммарная проводимость будет

равна Y , а комплексное сопротивление – Z . Две цепи с последовательными и параллельными соединениями, имеющие одинаковое сопротивление на выводах, называются эквивалентными (рис. 3.7):

	g				r1		, b						L1			,
	g		r	2	( L )2		, b			r	2 ( L )2					,
		1			1				1						1
	1	r2		( L )2							1			r2	( L )2
r		1			1	, L								1	1		.
2	g				r			2				b			r
					1										1

R2 L2

R1 L1

Рис. 3.7. Эквивалентные цепи

Причём условие эквивалентности цепей выполняется для одной

частоты, на которой найдено X.
При преобразовании параллельно соединённых элементов R2, L2	в
эквивалентную цепь последовательно соединённых элементов R1, L1	(рис.
3.8а), параметры этих цепей связаны соотношениями:

				1								1
r	g2			r2			;	L	b2			L2			.
					1
1	g22 b22		1					1	g22 b22		1		1
			2		2	2					2		2 2
			r		L						r			L
		2				2				2			2

Отформатировано:

английский (США)

Отформатировано:

английский (США)

Отформатировано:

английский (США)

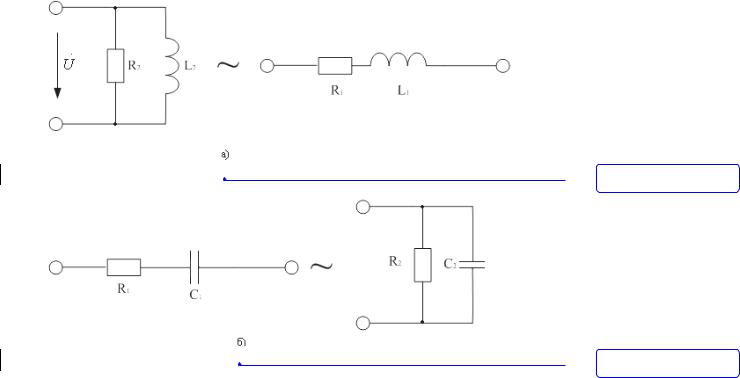
а)

б)

Рис. 3.8. Преобразование цепей:

а) параллельной в эквивалентную последовательную; б) последовательной в эквивалентную параллельную

Отформатировано: Шрифт: 12 пт

Параметры двух эквивалентных электрических цепей (рис. 3.8б), одна из которых содержит последовательно соединённые элементы R1, C1 , а другая – параллельно соединённые элементы R2, C2, связаны соотношениями:

r r (1		1			);C		C (		1		);
r r (1		( C r )2			);C		C (				);
2	1	( C r )2				2	1	1 ( C r)2
		1 1							1 1
r r (		1			);C C			(1	1			).
r r (			r )2		);C C			(1	( C r )2			).
1	2 1 ( C		r )2	1			2		( C r )2
		2	2						2	2

3.2. Смешанное соединение элементов

Электрическая схема, имеющая смешанное соединение элементов, может быть преобразована в более простую схему путём замены параллельных ветвей одной ветвью и её последовательно соединённых участков – одним участком. На рисунке 3.9 показана такая электрическая схема со смешанным соединением элементов. Приведём её к одноконтурной. Общий порядок выполнения действий при этом следующий. Первоначально вычисляется эквивалентная комплексная проводимость параллельных ветвей, затем находится комплексное сопротивление параллельных ветвей.

Последнее суммируется с комплексным сопротивлением Z1 последовательно

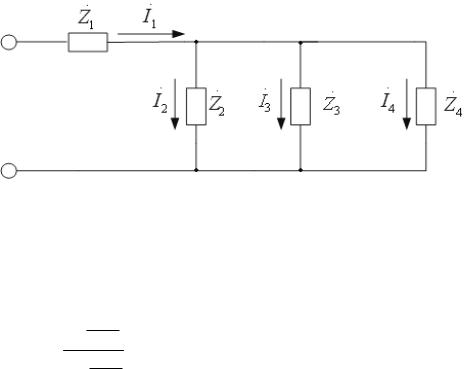
включённого участка. Полученное комплексное сопротивление эквивалентно сопротивлению исходной цепи со смешанным соединением:

													1			1			1		. .			. .	. .
.	.			.				.					1			1			1			Z2 Z3 Z 4 Z3 Z2 Z 4
Y э Y 2 Y3 Y 4																										;
Y э Y 2 Y3 Y 4													.				.			.				. . .		;
													Z 2				Z3			Z4				Z2 Z3 Z4
																. . .
. .				1				.								Z 2 Z3 Z 4
Z Z	1					Z1																	.
Z Z	1		.			Z1						. .				. .					. .		.
		Y э										Z2 Z3 Z 4 Z3 Z2 Z 4
						.		.
								.
Суммарный ток I							U			.
Суммарный ток I										.
				1 .
						.		Z							.
						.			.						.	.
									.							.
		.				.			Y .						.		Y
Токи в ветвях: I					I					2	;I			I				3	.
Токи в ветвях: I				2	I			1	.		;I		3	I		1 .			.
				2				1	.				3			1 .

Yэ Yэ

Рис. 3.9. Электрическая схема со смешанным соединением элементов

Рассмотрим схему со смешанным соединением элементов (рис. 3.10а). Найдём значения R и C, при которых схемы а) и б) рисунка 3.10 эквивалентны.

Z. r1 j L1 r2 j 1C1 r2 j C1

r	j L	r	r		r		j L	2 j r2C
		2				2		2 1		.
		1 j C r
1	1		1	1 r С 2			1	1 2C2r2
		1 2		2		1		1	2

а)

б)

Рис. 3.10. Схема со смешанным соединением

Для схемы рисунка 3.10б:

Z r

Поэтому:

r r1

;

1 2C2r2

( L

r2C

);

1 2C2r2

(

2 1

L )

1 2C2r2

3.3. Преобразование треугольника в звезду и обратное преобразование

Эквивалентным преобразованием «Треугольника» в «Звезду» называется такая замена части цепи, соединённой по схеме «Треугольник», цепью, соединённой по схеме «Звезда», при которой токи и напряжения в остальной части цепи остаются неизменными. Иначе говоря, при одинаковых напряжениях между выводами 1–3 (3–2, 2–1) и для «Треугольника», и для «Звезды» входящие в них токи одинаковы (рис. 3.11), т.е. мощности в этих цепях одинаковы. Рассмотрим преобразование треугольника в эквивалентную звезду, используя схемы а) и б) рисунка 3.11.

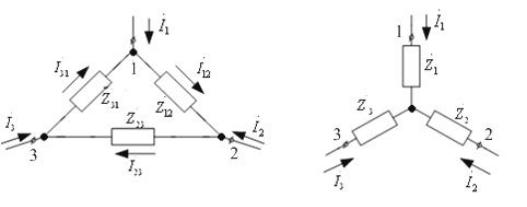
а)

б)

Рис. 3.11. Преобразование треугольника в эквивалентную звезду

Для сопротивлений, соединённых по схеме треугольника, по второму закону Кирхгофа можем записать:

. . . . . .

Z12 I12 Z23 I23 Z31 I31 0.

Уравнения, записанные по первому закону Кирхгофа для узлов 1, 2, будут иметь вид:

. . . . . .

I23 I12 I2, I31 I12 I1 .

Решая эти уравнения относительно I12 , получим:

							. . . .
				.			Z			I		Z				I	2
				I12			31				1				23		2		.
				I12			.				.				.				.
			.				Z12 Z23 Z31
Тогда напряжение U12				будет равно:
							. . . . . .
		.	. .					Z	12	Z		31		I	1	Z		12		Z	23	I	2
		U	I	Z	12				12			31			1			12			23		2	.
		12	12		12						.					.				.
										Z12 Z23 Z31
В схеме (рис. 3.11б) напряжение определяется выражением:
				.			. . . .
				U12 I1 Z1 I2 Z 2 .																	.
																					.
Для эквивалентности необходимо равенство U12 при любых токах,
т.е.:									. .
		. .							. .				23
		Z12 Z31		.				Z12 Z					23				.				. . . .
				I1													I2 I1 Z1 I2 Z 2 .
	.	.	.	I1		.				.					.		I2 I1 Z1 I2 Z 2 .
	Z12 Z 23 Z31					Z12 Z 23 Z31

Откуда:

	. .		31						. .	23
.	Z	12 Z	31		.				Z12 Z	23
Z1					; Z2						.	(3.2)
Z1	.	.	.		; Z2		.		.	.	.	(3.2)
	Z12 Z23 Z31						Z12 Z23 Z31
			. .
		.		Z	23 Z31
Аналогично найдём: Z3								.				(3.3)
Аналогично найдём: Z3				.	.	.		.				(3.3)
				Z12 Z23 Z31

Рассмотрим преобразование «Звезды» в эквивалентный «Треугольник». Исследуем полученные выражения (3.2) – (3.3). Поделив третье на второе и на первое, получим:

					.		.						.			.
				Z				Z			и	Z		3			Z		31	.
						3		23						3					31
					.			.					.				.
				Z1				Z12				Z2					Z12
.		.									.												.
Выражая Z 23 и		Z31				через					Z12			и		подставляя в формулу для Z1
выражения (3.2), имеем:
							.								.						. .
. .						.			Z	3	.				Z	3					2 Z		3
Z		(Z			Z					3	Z					3		) Z					3	.
Z	1	(Z	12		Z		12 .				Z		12		.			) Z			12 .			.
									Z1						Z2							Z2

Откуда:

. .

.	. .			Z Z			2
Z	Z Z			1			2		.
Z	Z Z			.					.
12		1	1	.
Аналогичным образом найдём:					Z3
Аналогичным образом найдём:
				. .
.	. .				Z	Z		2
Z23 Z2 Z3						3		2			;
Z23 Z2 Z3						.					;
						Z1
				. .
.	. .			Z Z			3
Z	Z	3	Z	1			3			.
Z	Z		Z							.
13			1			.
					Z2

Таким образом, комплексное сопротивление стороны «Треугольника» равно сумме комплексных сопротивлений прилегающих «лучей» «Звезды» и их произведения, делённого на сопротивление третьего «луча». Токи в «лучах» звезды:

. . . . . . . . .

I1 I12 I31 ; I2 I23 I12 ; I3 I31 I23 .

3.4. Эквивалентные преобразования активных двухполюсников

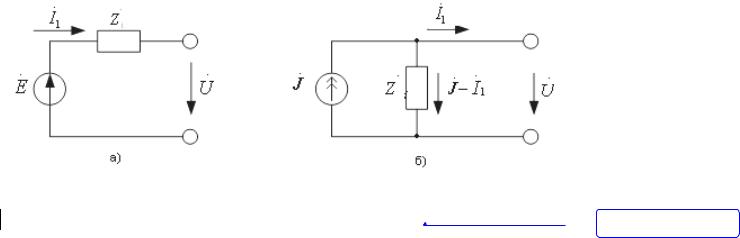
При расчёте электрических цепей зачастую возникает необходимость в

. .

переходе от источника э.д.с. E к источнику тока J , и наоборот. Источник э.д.с. и источник тока считаются эквивалентными, если при замене одного источника другим токи и напряжения во внешней цепи, с которой эти источники соединяются, остаются неизменными. Найдём условие эквивалентности преобразования источников, используя схемы а) и б) рисунка 3.12.

									.			. . . .
	Для рисунка 3.12а напряжение U на выводах равно: U E I1 ZU .
Для рисунка 3.12б это же напряжение определится выражением:
.	.
U (J I ). Приравняем правые части выражений:
	1
						. . .			. .
						E I		Z	J Z	I .
								1 U	i		1
				.		.		.			.
				.		.		.			E
				и Z		Z	Z				E
	Откуда Е J	Z	i	и Z	i	Z	Z		или J		.	.
			i		i	U					.

Рис. 3.12. Эквивалентные источники э.д.с. и тока

а)

б)

Мощности, расходуемые на внутренних сопротивлениях источников э.д.с. и тока, неодинаковы. Эквивалентность источников следует понимать только в смысле неизменности токов, напряжений и мощностей во внешней электрической цепи, присоединённой к источникам.

Рассмотрим преобразование схем с двумя узлами (рис. 3.13). Заменяя источники э.д.с. источниками токов, получим схему (рис. 3.13б), причём:

Отформатировано: Шрифт: 12 пт

			.			.				.
. .	.	.		E	1		E	2			En		n . .
J J1 J2		... Jn		E	1		E	2		...	En		Y k Ek ,
J J1 J2		... Jn		.			.			...	.		Y k Ek ,
				Z	1		Z	2			Z	n	k 1
					1			2				n
			.			1
			Z						.
			Z			n .			.

Y k

k 1

а)	б)	Отформатировано: Шрифт:
а)		12 пт
		Отформатировано: Шрифт:
		12 пт

Рис. 3.13. Преобразование схем с двумя узлами

в)

г)

Используя данное соотношение, можно перейти к схеме (рис. 3.13г):

				n . .
. .	. Y k				Ek
E Z J			k 1				.
E Z J			n .				.
				Y	k
Ток внешней цепи:				k 1	k
Ток внешней цепи:				.
				.
.	.			Z
In 1	J					,
In 1	J	.		.		,

Z Zn 1

напряжение:

. .

U. J. ( Z. Zn .1 ).

ZZn 1

3.5.Перенос источников

Вряде случаев расчёт электрической цепи облегчается в результате переноса в схеме источников э.д.с. или тока. Из второго уравнения Кирхгофа следует, что токи в схеме определяются заданными величинами суммарных э.д.с. в контурах независимо от того, из каких отдельных слагающих они

Отформатировано: Шрифт: 12 пт

<<< < Предыдущая 1 2 3 4 56 / 96 7 8 9 > Следующая >>>

Соседние файлы в папке ОТЦ модули

#
09.02.20151.29 Mб22М1_ОТЦ_1.pdf
#
09.02.20151.05 Mб24ОТЦ_Модуль2.pdf