
ОТЦ модули / М1_ОТЦ_1
.pdf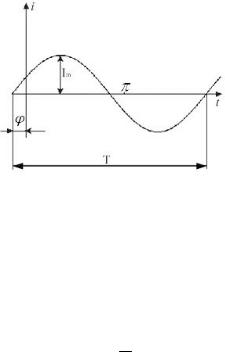
управления, каналов радиосвязи и т.д. Задача синтеза обычно сводится к нахождению цепи по заданной частотной характеристике. В отличие от задачи анализа, она может иметь несколько решений или вовсе их не иметь в заданном классе электрических цепей.
2. ЛИНЕЙНЫЕ ЦЕПИ ПРИ ГАРМОНИЧЕСКОМ ВОЗДЕЙСТВИИ
2.1. Гармонические величины и их основные параметры
Гармонической называется периодическая функция, значения которой изменяются во времени по синусоидальному или косинусоидальному закону. В теории электрических цепей такими величинами являются токи и напряжения.
Мгновенное значение гармонического тока определяется выражением:
i Im |
sin( t ) Im |
cos( t |
|
). |
|
||||
|
|
2 |
|
|
Аналогичным выражением определяется мгновенное значение гармонического напряжения. График изменения гармонического тока изображён на рисунке 2.1.
Рис. 2.1. Графическое изображение гармонического тока
Наименьшее время, по истечении которого повторяются мгновенные значения гармонического тока, называется периодом – T.
Величина, обратная периоду и численно равная числу периодов в единицу времени, называется частотой колебаний функции f:
f 1 . T
Амплитудой Im гармонического тока называется максимальное значение функции i(t).
Аргумент t называется мгновенной фазой |
тока. Фаза |
отсчитывается от точки перехода тока через нуль (максимум) |
к положи- |
тельному значению.
Скорость изменения мгновенной фазы тока носит название угловой
частоты : |
2 . |
2 f ; |
T
Начальная фаза – величина аргумента, соответствующая значению гармонически изменяющегося тока в начальный момент времени t=0.
Для генерирования гармонических величин используют генераторы гармонических колебаний.
2.2. Среднее и действующее значения гармонической функции
Среднее значение периодической функции f(t) за период T определяется по формуле:
1 T
Fср T 0 f (t)dt.
T
Для синусоидальной величины f (t)dt=0, поэтому в этом случае
0
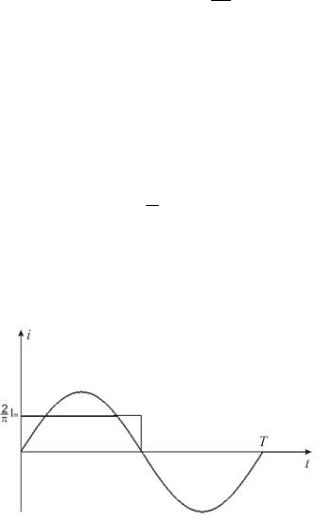
пользуются понятием среднего полупериодного значения, соответствующего положительной полуволне синусоиды (рис. 2.2).
Рис. 2.2. Среднее полупериодное значение С учётом этого среднее значение гармонического тока равно:
|
|
2Im |
|
Т |
2Im |
|
|
|
|
T |
|
Im |
|
Im |
|
||
|
|
|
2 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
I |
СР |
|
|
0sin t dt |
|
( cos t) |
|
02 |
|
|
(1 1) 2 |
|
0,637 Im. |
||||
T |
T |
|
|
||||||||||||||
|
|
|
|
|
|||||||||||||
|
Аналогично для напряжения: |
|
|
|
|
|
|||||||||||
|
|
|
|
|
UСР |
2 |
Um |
0,637 Um . |
|
|
|||||||
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Наряду со средним значением гармонический ток характеризуется среднеквадратичным или действующим значением. Выбор такой
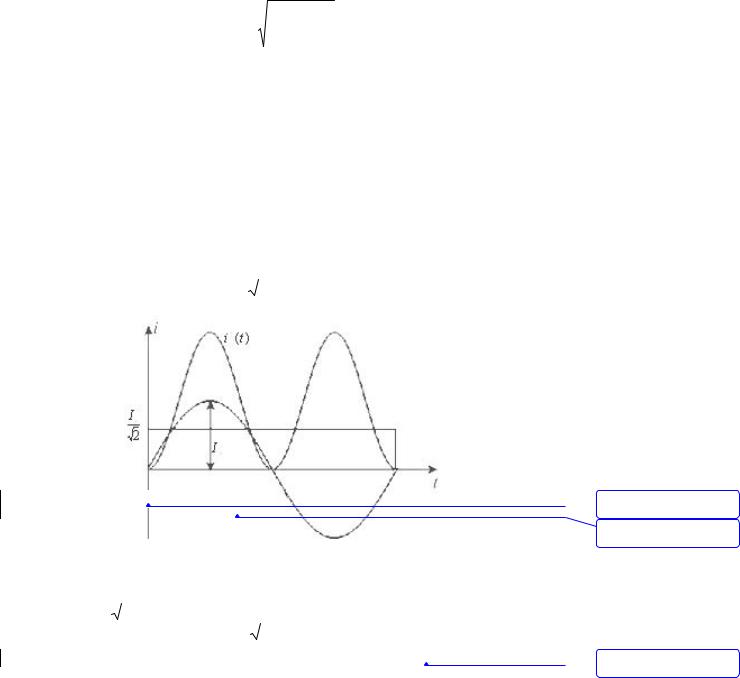
характеристики обусловлен тем, что тепловое действие тока и механическая сила взаимодействия двух проводников с током пропорциональны квадрату тока.
Действующее значение гармонического тока равно:
|
1 |
T |
2 |
|
I |
|
i |
|
dt . |
T |
|
|||
|
0 |
|
|
Для того чтобы уяснить смысл данного равенства, возведём его в квадрат и умножим обе части на RּT:
T
R I2 T R i2 dt.
0
Это равенство показывает, что действующий гармонический ток равен такому постоянному току, который, проходя через неизменное сопротивление R за период времени T, выделяет то же количество тепла, что и гармонический ток i. Найдём значение I (рис. 2.3):
|
|
1 |
T |
I |
2 T |
|
|
I2 |
I |
2 |
|
1 |
|
|
T |
|
I2 |
|||||
I2 |
|
Im2 sin2 t dt |
m |
|
|
|
|
|
m |
|
|
|
|
|||||||||
|
|
|
(1 cos2 t) dt |
m |
|
|
|
|
|
sin2 t |
0 |
|
m |
, |
||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
2 2T 2 |
|
|
2 |
|
|||||||||||||
|
|
T 0 |
2T 0 |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
I |
I |
m |
|
0,707 Im. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
i
i (t)
Рис. 2.3. К нахождению действующего значения гармонического тока
АналогичноI действующее напряжение:
m
|
2 |
I U |
U |
m |
|
0,707 I |
m |
. |
|
|
|
|
|||||
|
|
|||||||
|
|
m |
|
|
|
|||
|
|
2 |
|
|
|
|
||
t
2.3. Сопротивление, индуктивность и ёмкость при гармоническом воздействии
 Отформатировано: Шрифт: 12 пт, курсив
Отформатировано: Шрифт: 12 пт, курсив
Отформатировано: Шрифт: 12 пт, курсив
 Отформатировано: Шрифт: 12 пт, курсив
Отформатировано: Шрифт: 12 пт, курсив
Если к сопротивлению R подвести гармоническое напряжение u Um sin( t ), то через него потечёт ток:
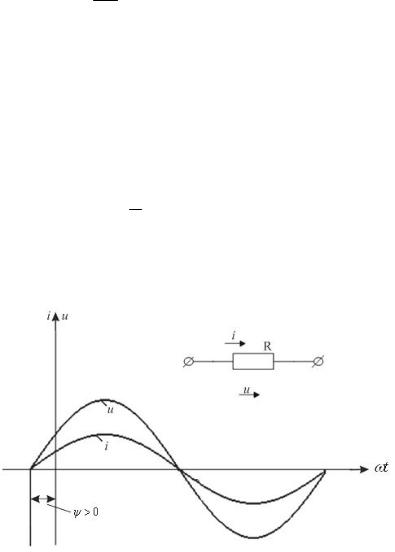
i Um sin( t ) Im sin( t ).
R
Из полученного выражения видно, что напряжение и ток имеют одинаковую начальную фазу, т.е. их разность фаз, или фазовый сдвиг, равны 0 (рис. 2.4). Не только мгновенные значения, но и амплитудные и действующие значения напряжения и тока, протекающего через сопротивление, связаны законом Ома:
Um R Im, U R I .
Для проводимости g 1 выражения будут иметь вид:
R
Im g Um, |
I g U . |
Мгновенная мощность сопротивления равна:
pR u i Um Im sin2( t ) U I (1 cos2( t )).
Рис. 2.4. Сопротивление при гармоническом воздействии
Из выражения видно, что мгновенная мощность pR содержит две составляющие: постоянную, равную произведению действующих значений напряжения и тока, и переменную, изменяющуюся с удвоенной угловой частотой (рис. 2.5). Максимальное значение мгновенной мощности равно 2ּUּI, а минимальное – нулю. Мгновенная мощность сопротивления всегда положительна.
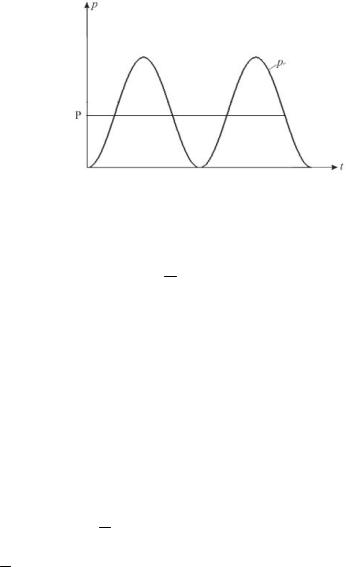
Рис. 2.5. Мгновенная и средняя мощности, поступающие в сопротивление
Среднее значение мощности сопротивления P за период называется активной мощностью и определяется выражением:
1 T
P T 0 pR dt U I .
Она характеризует среднюю за период скорость потребления сопротивлением энергии от источника. Величина R в цепи переменного тока называется активным сопротивлением.
Пусть ток i Im sin( t ) протекает через индуктивность L. Найдём э.д.с. самоиндукции:
eL L |
di |
L Im |
cos( t ) Um sin( t |
|
). |
|||
|
|
|||||||
|
dt |
|
2 |
|
||||
Напряжение на индуктивности будет равно: |
||||||||
|
|
uL eL |
|
Um sin( t |
|
). |
||
|
|
|
|
|||||
Из данного выражения |
|
2 |
|
|
|
|||
видно, что напряжение на индуктивности |
||||||||
опережает ток на угол : максимум напряжения смещён влево относительно
2
тока на (рис. 2.6). Фазовый сдвиг тока относительно напряжения, под
2
которым понимается разность начальных фаз напряжения u и то- |
ка i , |
||||
равен |
|
: |
|
|
|
|
|
|
|
||
2 |
|
|
|
||
|
|
= u - i = |
|
||
|
|
|
. |
|
|
|
|
2 |
|
||
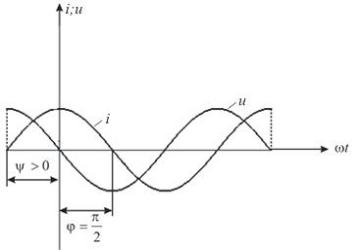
Рис. 2.6. Графики тока и напряжения индуктивности при гармоническом воздействии
Амплитуды и действующие значения токов связаны соотношением, подобным закону Ома:
Um L Im xL Im , U I L xL I .
Величина xL L, имеющая размерность сопротивления, называется
индуктивным сопротивлением, а обратная ей величина b |
|
1 |
– |
|
|||
L |
|
L |
|
индуктивной проводимостью. Индуктивное сопротивление представляет собой расчётную величину, с помощью которой учитывается явление самоиндукции.
Мгновенная мощность индуктивности равна:
pL Um Im sin( t ) sin( t |
|
) |
Um Im |
(sin( t ) 2cos( t )) U I sin2( t ). |
||||||||
|
|
|||||||||||
|
|
|
2 |
|
2 |
|
|
|
|
|||
Таким образом, мгновенная мощность pL |
колеблется с частотой 2 , а |
|||||||||||
её среднее значение равно нулю. |
|
|
|
|
|
|
||||||
Энергия магнитного поля индуктивности рассчитывается по формуле: |
||||||||||||
|
L i2 |
|
L I2 |
|
|
|
L I |
2 |
|
|||
wL |
|
|
m |
sin2 |
( t ) |
|
|
(1 cos2( t )). |
||||
|
2 |
|
|
|||||||||
2 |
|
|
|
|
2 |
|
|
|||||
Поступая от источника, энергия временно запасается в магнитном поле индуктивности, затем возвращается в источник при исчезновении магнитного поля. То есть происходит колебание энергии между источником и индуктивностью, причем активная мощность в индуктивность не поступает. Временные диаграммы, энергии, мощности, тока и напряжения индуктивности представлены на рисунке 2.7.
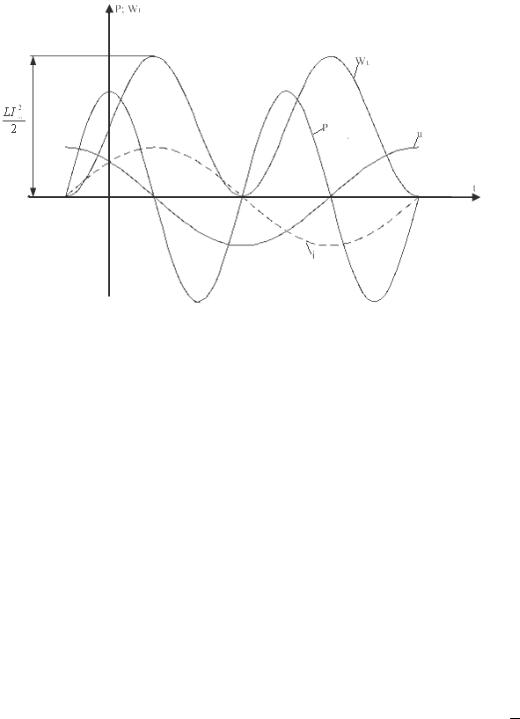
Рис. 2.7. Временные диаграммы тока, напряжения, мощности и энергии для индуктивности
Поскольку
wLmax L I2 , то xL |
L |
wLmax |
. |
|
|
|
||||||
|
|
|
||||||||||
|
|
|
|
|
|
|
|
I2 |
|
|
||
Рассмотрим ёмкость в цепи гармонического тока. Пусть напряжение |
||||||||||||
на ёмкости равно: |
|
|
|
|
|
|
||||||
|
|
|
|
|
u Um sin( t ). |
|
|
|||||
Учитывая, что i C |
du |
, получим: |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
||||||
|
|
du |
|
|
dt |
|
|
|
|
|
|
|
i C |
|
C Um cos( t ) Im sin( t |
). |
(2.1) |
||||||||
|
|
|
||||||||||
|
|
dt |
2 |
|
|
|||||||
Величина xC |
1 |
, имеющая размерность сопротивления, |
называется |
|||||||||
|
||||||||||||
|
|
С |
ей величина bC C |
|
|
|||||||
ёмкостным сопротивлением. Обратная |
называется |
|||||||||||
ёмкостной проводимостью. |
|
|
|
|
|
|
||||||
Из выражения (2.1) видно, что ток опережает напряжение на угол .
2
Временные диаграммы тока и напряжения на ёмкости представлены на рисунке 2.8.

Рис. 2.8. Временные диаграммы тока и напряжения на ёмкости
Найдём мгновенную мощность, поступающую в ёмкость:
pL |
u i Um Im |
sin( t )sin( t |
|
) U I sin2( t ). |
|
||||
|
|
2 |
|
|
Из полученной формулы видно, что мгновенная мощность колеблется с частотой 2 , и её среднее значение равно нулю.
Энергия электрического поля ёмкости определится выражением:
|
|
C u2 |
|
C U 2 |
|
wL |
|
|
|
m |
sin2 ( t ) C U (1 cos2( t )). |
|
2 |
||||
|
2 |
|
|
||
Рис. 2.9. Временные диаграммы тока, напряжения, мощности и энергии ёмкости
Она поступает от источника, временно запасается в электрическом поле ёмкости, а затем возвращается в источник при исчезновении электрического поля. Таким образом, как и в случае индуктивности, происходит колебание энергии между источником и ёмкостью, причём активная мощность P=0. Временные диаграммы представлены на рисунке
2.9.

2.4. Простейшие линейные цепи при гармоническом воздействии
Рассмотрим линейную электрическую цепь, состоящую из последовательно соединённых сопротивления R, индуктивности L и ёмкости
C (рис. 2.10). При протекании в цепи тока |
i Im sin t синусоидальное |
напряжение на её входе будет равно: u uR uL |
uC . |
Рис. 2.10. Пример простейшей линейной цепи
Напряжение uR на сопротивлении R совпадает по фазе с током i,
напряжение uL опережает, а напряжение uC |
отстаёт по фазе от тока на |
|
. |
|
|||
Учитывая это, получим: |
2 |
|
|
|
|
|
|
U |
sin t r I |
|
sin t L I |
|
cos t |
1 |
I |
|
cos t |
||||||
|
|
|
|
||||||||||||
m |
|
|
|
m |
|
|
|
|
|
m |
|
C |
m |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
r |
Im |
sin t |
L |
|
|
Im |
cos t Im (rsin t xcos t). |
||||||||
|
|||||||||||||||
|
|
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
Полученное уравнение представляет собой тригонометрическую форму записи второго закона Кирхгофа для мгновенных напряжений. Величина
x xL xC |
L |
1 |
называется реактивным сопротивлением цепи, |
|
C |
||||
|
|
|
которое может иметь индуктивный характер, когда x>0, и ёмкостной характер, когда x<0.
С учётом тригонометрического соотношения
msin ncos 
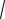 m2 n2 sin( ),
m2 n2 sin( ),
где arctg n , m
получим: |
Um |
r2 x2 Im , |
(2.2) |
||
|
|
arctg |
x |
. |
(2.3) |
|
|
|
|||
r
Полученное соотношение (2.2) фактически представляет собой закон
Ома, если обозначить z 
 x2 r2 :
x2 r2 :
Um z Im .
|
|
|
r2 ( L |
1 |
)2 |
|
|
Величина z |
x2 r2 |
|
называется полным |
||||
|
|||||||
|
|
|
|
C |
|
||
сопротивлением рассматриваемой цепи. Активное, реактивное и полное сопротивления являются основными понятиями в теории цепей.
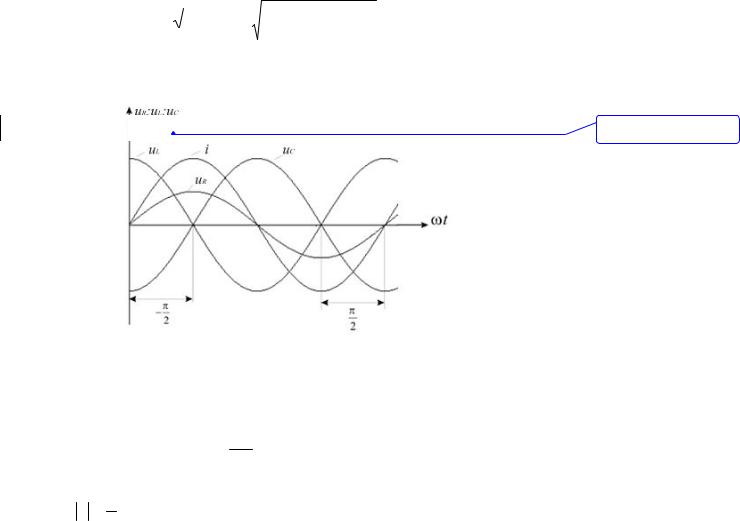
uRuLuC
Рис. 2.11. Временные диаграммы токов и напряжений цепи
Выражение (2.3) определяет фазовый сдвиг между напряжением и током. Если напряжение u=Umּsin( t+ ), то ток определяется выражением:
i Um sin( t ). z
Угол отсчитывается по оси t в направлении от напряжения к току
и всегда . Фазовый сдвиг >0, когда x>0. При этом ток отстаёт по фазе
2
от напряжения и отсчитывается по оси абсцисс вправо от «u» к «i». <0, когда x<0. При этом ток отстаёт по фазе от напряжения и отсчитывается по оси абсцисс влево от «u» к «i» (рис. 2.11).
При x=xL-xC=0 ток совпадает по фазе с напряжением, т.е. =0. Такой режим работы электрической цепи рисунка 2.10 называется резонансом напряжений.
Активное и реактивное сопротивления связаны с полным сопротивлением формулами:
r=zּcos ; x=zּsin . |
|
|
|
Составляющая напряжения |
Ua I r z I cos U cos |
называется |
|
активной составляющей, а Up |
I x z I sin U sin |
– |
реактивной |
составляющей напряжения. |
|
R, L и C |
|
Рассмотрим параллельное |
соединение элементов |
||
(рис. 2.12). |
|
|
|
Отформатировано:
английский (США)
