Лекция 2. Функциональные ряды

Добавил:

Rin_Yano Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Сибирский Государственный Университет Путей Сообщения

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Подставим x1 1 в ряд

..pdf

Скачиваний:

Добавлен:

06.10.2022

Размер:

686 Кб

Скачать

☆

Пожидаев А.В., Вылегжанин И.А.Математика: Курс лекций для студентов технических специальностей. Ч. IV. – Новосибирск: Изд-во СГУПСа, 2009. – 138 с.

Лекция № 2

ФУНКЦИОНАЛЬНЫЕ РЯДЫ

Степенные ряды. Интервал и радиус сходимости. Теорема Абеля. Ряды Тейлора и Маклорена. Разложение функций в степенные ряды. Применение степенных рядов в приближенных вычислениях.

Степенные ряды

Рассмотрим

последовательность

функций

f1 x , f2 x ,..., fn x ...и составим из них ряд

x .

f1 x f2 x ... fn x ... fn

n 1

Определение: Ряд

f1 x f2 x ... fn x ... fn x называется функциональным рядом.

n 1

fn x

Примеры: 1)

, fn x

...

n 1

x x x2 x3 ...

fn x xn , fn

n 1

fn x sinnx , fn x sin x sin2x sin3x ...

n 1

Если в функциональный ряд вместо переменной x подставить какое-либо число, получится сходящийся или расходящийся числовой ряд. Пусть X - множество всех значений переменной

x, при которых ряд fn x сходится. Тогда можно говорить, что на множестве чисел X

n 1

определена функция одной действительной переменной F(x) fn x , значениями которой

n 1

являются суммы соответствующих числовых рядов.

Определение:Множество чисел X , при которых сходится ряд fn x , называется областью

n 1

сходимости этого ряда.

fn x an x x0 n ,

Определение:

Если

где x0 ,an - действительные числа, то ряд

a1 x x0 a2 x x0 2

an x x0 n a0

...

называется степенным рядом.

n 0

x 1 2 x 1 2 3 x 1 3 ...,

Примеры: xn

x x2

x3 ...,

n x 1 n

n 0

1 x

...

n 0

Теорема Абеля1 (об интервале сходимости) Областью сходимости степенного ряда
	n является открытый, полуоткрытый или замкнутый интервал с концами в точках
an x x0
n 0
x0 R и x0	R, где R некоторое действительное число или .
Доказательство: Рассмотрим сначала ряд

	an xn a0 a1x a2 x2 a3x3 ....
	n 0

Этот ряд обязательно сходится при x 0. Допустим, что этот ряд сходится еще в какой-либо

точке x , тогда по необходимому признаку сходимости, lima

xn 0 и, значит, найдется число

M такое, что

M для всех номеров n. Возьмем любое число x

такое, что

, и

n 1

составим ряд

an x2n

. Поскольку

n 0

x2n

n 1

и ряд

, будучи геометрической прогрессией со знаменателем q

1, сходится, то по

n 0

теоремео сходимости и арифметических операциях сходится ряд M

. Тогда, по признаку

n 0

сравнения

будет

сходиться

ряд

an x2n

. Поскольку

произвольное

число,

n 0

удовлетворяющее условию

, то ряд an xn будет сходиться в любой точке интервала

x1,x1 .

n 0

Рассмотрим теперь ряд an x x0 n

и, сделав замену переменной

y x x0 , получим ряд

n 0

который сходится на некотором интервале y y1, y1 . Возвращаясь к переменной

an yn ,

n 0

сходится на интервале x0

y1 . Теорема доказана.

x, получим, что ряд an x x0 n

y1,x0

n 0

Замечание: В частности, интервалом сходимости степенного ряда может оказаться единственная точка x0 или вся числовая прямая.

n можно применять

Для практического нахождения интервала сходимости ряда an x x0

n 0

метод Даламбера, состоящий в следующем: рассматривается предел

lim

n 1

x x

n 1

x x

lim

n 1

x x0

Еслиэтотпределменьше1,топопризнакуДаламбера,рядсходится,еслибольше–расходится.

Решая неравенство	x x	0	lim	an 1	1, находим открытый интервал, в точках которого ряд
				an 1
				a
			n
			n
				n

сходится.Внеэтогоинтервалазаисключением,можетбыть, концовинтервала,рядрасходится.

1 Абель Нильс Хенрик (1802-1829) норвежский математик. Доказал, что алгебраические уравнения степени выше 4-ой неразрешимы в радикалах. Один из создателей теории эллиптических функций, автор первой работы по интегральным уравнениям. Труды по теории чисел и рядов.

Для проверки сходимости на концах интервала нужно подставить каждое из этих двух чисел в формулу ряда и, получив числовые ряды, проверить их сходимость.

Пример1: Найти интервал сходимости ряда 1 n 1 xn

n 1 n

Решение: lim

1 n 2 xn 1

lim

n 1

1 n 1 xn

n 1

lim

. Решаем неравенство

n n 1

Теперь проверяем сходимость на концах интервала:

x 1;1 .

n 1

2n 1

1 . Гармонический ряд расходится.

n 1

Подставим точку

x2 1:

Получили знакочередующийся ряд,

n 1

удовлетворяющий условиям признака Лейбница:

lim

0. Значит, ряд сходится.

n 1

n n

Следовательно, интервалом сходимости данного ряда будет 1;1 .

Пример 2: Найти интервал сходимости ряда

n 0

Решение: lim

xn 1

lim

0 0

n 1!

Полученное неравенство 0 1верно при любых значениях переменной x, т. к. не зависит от этой переменной. Значит, ряд сходится при любых значениях переменной и его интервалом сходимости является ; .

Пример 3: Найти интервал сходимости ряда n!xn .

n 1!xn 1

n 0

Решение: lim

lim

n 1

n!xn

При любом значении переменной x 0 предел будет равен . При x 0

получается неопределенность 0 .

Поэтому проверим сходимость непосредственной

подстановкой: n!0n 0 0 0 ... 0. Ряд сходится.

n 0

Значит, данный ряд сходится в единственной точке x 0.

Формула Тейлора2

Рассмотрим производные многочлена p x a

a x a

... a

p' x a

x 3a

x2 ... na

xn 1

p'' x 2a2

2 3a3x ... n n 1 an xn 2

p''' x 2 3a3x ... n n 1 n 2 an xn 3

…………………………………………………

2 Тейлор Брук (1685-1731) английский математик.

p n x n n 1 n 2 ... 3 2an

При x 0получим:

p 0 a0

0!a0

p' 0 a 1!a

p'' 0 2a2

2!a2

p''' 0

2 3a3

3!a3

……………………….

p 0

p(n)

n n 1 ... 3 2an n!an

Значит,

p' 0

'' 0

,…., a

p n 0

p x

p 0

p' 0

p'' 0

...

p n 0

p i 0

i 1

Если в этой формуле заменить x на x x0 , получим общую формулу

p x

p x0

p' x0

x x0

p'' x0

x x0

2 ...

p n x0

p i x0

x x0

i 1

называемую формулой Тейлора для многочлена.

Пусть

f x

произвольная

функция,

имеющая в точке

производные

f ' x0 , f '' x0 ,...,

f n x0 . Сопоставим этой функции многочлен

pn x

f x0

f ' x0

x x0

f '' x0

x x0 2 ...

f n x

i x

i 1

Теорема (о порядке приближения функции многочленом) Пусть

f x

произвольная

функция,

имеющая

точке

производные

f ' x0 , f '' x0 ,..., f n

, и пусть

pn x n f i i!x0 x x0 i , тогда

i 1

f x pn x o x x0 n

Доказательство: обозначим rn x f x pn x . Из определения многочлена	pn x следует,
что

r' x

r'' x

... r n x

r1 x r x0

При n 1 получим:

lim

r1 x

lim

r1 x 0

lim

r1' x0 0 .

x x0

При n 2 получим:

lim

r2 x

lim

r2' x

lim

r2' x r2' x0

r'' x

здесь

воспользовались

x x0 2

2 x x0

x x0

2 x x0

x x0

правилом Лопиталя. При n 3 получим:

lim

x x0

r x

lim

r'' x

lim

x x0

3 x x0 2

2 x x0

x x0

3 x x0

lim

r3'' x r3'' x0

r''' x

x x0

здесь дважды воспользовались правилом Лопиталя.	rk x
В общем случае для доказательства равенства lim		0	нужно будет n 1раз
	x x0 k
x x0

воспользоваться правилом Лопиталя. Теорема доказана.

Замечание: из доказанной теоремы следует, что формулу Тейлора можно использовать для вычислений приближенных значений дифференцируемых функций:

f x

' x

f ''

f n x

f i x

f x

x x0

...

x x0

x x0 ,

i 1

причем, чем больше число n ,

тем приближение лучше. Данная приближенная формула

называется формулой Тейлора. При x0

0 ее также называют формулой Маклорена3.

Пример:

Рассмотрим

функцию

f x cosx

и составим

для нее

формулы

Тейлора при

n 0,1,2,3,4 и x0

f ' x sin x; f '' x cosx; f ''' x sin x; f 4 x cosx f ' 0 0; f '' 0 1; f ''' 0 0; f 4 0 1.

p0 x f (0) 1

p x f (0) f ' 0 x 1 0 x 1

x f (0) f '

0 x

x f (0) f ' 0 x

f '' 0

f ''' 0

x f (0) f ' 0 x

f '' 0

f ''' 0

4 0

x4 1

f '' 0 x2 1 x2

2 2

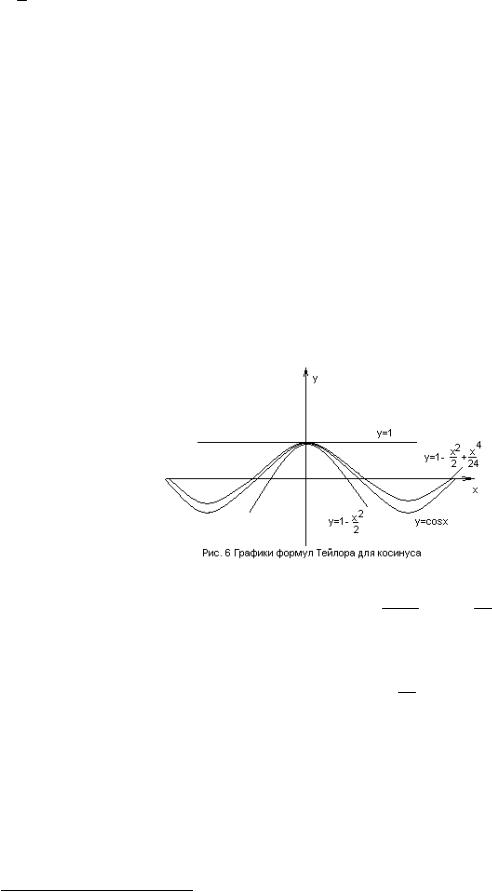
Каждый следующиймногочлен четной степенивселучше и лучше будетприближатьфункцию f x cos x на все большем и большем интервале.

Ряд Тейлора

Пусть функция f x имеетнапромежутке x x0 ,x x0 производныелюбыхпорядков.Тогда,

в связи с тем, что формула Тейлора при увеличении степени n все лучше и лучше приближает функцию, естественно считать

3 Маклорен Колин (1698-1746) – шотландский математик. Труды по математическому анализу, теории кривых, механике.

f x0

' x0

x x

f '' x0

x x0

2 ...

f n x0

f i x0

...

x x0 .

i 1

f i

Определение: Степенной ряд

x x0

называется рядом Тейлора функции f x .

i 0

При

x0 0

этот

ряд

называют

также

рядом

Маклорена.

Функцию

f i x0

rn x f x

x x0 o x

называют остатком ряда Тейлора.

i 1

Пример 1: Найдем ряды Маклорена

функций

y ex ,

sin x,

cosx ,

ln 1 x ,

1 x .

... y n ... ex , y 0 y' 0 y'' 0 ... y n 0 ... e0 1.

Решение: 1)

y ex : y'

y''

x2 ...

n 0

Впредыдущей лекции было показано, что интервал сходимости степенного ряда xn равен

i 0 n!

; .

2) y sin x:

y' cosx, y'' sin x, y''' cosx, y 4 sin x и т. д.

y 0 0, y' 0 1, y'' 0 0, y''' 0 1, y 4 0 0 т.е. последовательность значений

производных в точке 0 выглядит так: 0,1,0,-1,0,10,-1,0,1,0,-1 и т.д.

		1		1			1	n 1	x	2n 1
sin x 0			x 0		x3	...
							2n 1!
	1!			3!		n 0

Можно показать, что промежутком сходимости этого ряда также будет вся числовая прямая

;

3) y cosx: y' sin x, y'' cosx, y''' sin x, y 4 cosx и т.д.

y 0 1, y' 0 0, y'' 0 1, y''' 0 0, y 4 0 1 т.е. последовательность значений производных

в точке 0 выглядит так: 1,0,-1,0,10,-1,0,1,0,-1,0 и т.д.

cosx 1 0

...

2n !

n 0

И здесь можно показать, что промежутком сходимости этого ряда также будет вся числовая прямая ; .

y ln 1 x :

y' 1 x 1 ,

y'' 1 x 2 ,

y''' 21 x 3 ,

y 4 2 31 x 4 ,

y 5 2 3 41 x 5 .

Очевидно, что

y n 1 n 1

n 1! 1 x n и

y n 0 1 n 1 n 1!.

n 1

n 1!

n 1

Значит, ln 1 x 0

n 1

В предыдущей лекции было показано, что интервалом сходимости этого ряда является 1;1 .

5) y 1 x : y' 1 x 1 , y'' 1 1 x 2		, y''' 1 2 1 x 3 и т.д.
y 0 1, y' 0 , y'' 0 1, y''' 0 1 2 и т.д.
1 x 1 x 1 x2	1 2 x3	...
2!	3!

В частности, 1 1x 1 x x2 x3 ...,

Можно показать, что промежутком сходимости этого ряда является 1;1 .

Замечание: можно заметить, что в ряде Маклорена нечетной функции y sin x суммируются тольконечетныестепенипеременной,аврядеТейлорачетнойфункции y cosx суммируются

четные степени переменной. Это не случайно: можно доказать что у любой четной функции коэффициенты при нечетных степенях переменной в ряде Маклорена будут равны 0, а у нечетной функции будут равны 0 коэффициенты при четных степенях

Пример 2: составить ряды Маклорена функций y e x2 , y cos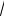x .

Решение: 1)

y e x2

: обозначим t x2 , тогда

y et

1 t t2

... 1 x2

...

2) y cos

: обозначим t

x , тогда

cost 1

... 1

...

Замечание: этот метод, называемый метод подстановки не всегда приводит к нужному результату. Например, при нахождении ряда Маклорена функции y sin 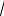x этот метод в ответе не дал бы степенного ряда.

Остаток ряда Тейлора в форме rn x o x x0 n не дает возможности вычислять значения

функции с заданной точностью, поэтому часто используются другие формы остатка, удобные для приближенных вычислений.

Пусть дана

функция

y f (x) на

промежутке

x0;x0

и существуют непрерывные

производные

f ' x , f '' x ,..., f n 1 x .

r x f x f x

f ' x0

x x

f '' x0

x x

f n x0

x x0 n

Зафиксируем некоторое число x x0;x0

и, заменив постоянную x0

на переменную z , составим вспомогательную функцию

z f x f z

f ' z

x z

f '' z

...

f n z

x z

Очевидно, что

x0 rn x , x 0.

Кроме того,

'''

z f

x z

...

f n 1 z

x z n

непрерывная на промежутке x0;x и такая, что на этом

Пусть x - некоторая функция,

промежутке ' x 0. Тогда по теореме Коши найдется число c x0 ;x такое, что

x x0

' c

x x0

' c

0 rn x

f n 1 c

x x0 n

Следовательно,

, откуда:

x x0

' c

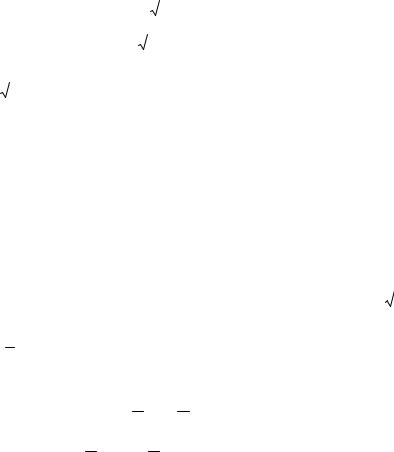
rn x		x x0		f	n 1 c	x c n . Различным образом	выбирая функцию x , можно

		' x			n!
получать различные					формы остатка. В частности,		если x x z n 1 , получим
rn x	f n 1 c		x x0 n		- остаток в форме Лагранжа.

	n 1!

Приближенные вычисления с помощью формулы Тейлора

Пользуясь формулой Тейлора с остатком в форме Лагранжа можно вычислять приближенные значения различных функций с заданной точностью

Пример 1: вычислить

e с точностью 0,01

Решение: поскольку

e0,5

и ex

, то

n 0 n!

1 0,5

0,5 2

0,5 3

...

0,5 n

r x . Нужно подобрать число n так, чтобы

f n 1 c

r x

x x

0,5 0 n

0,01

, где c 0;0,5

. Поскольку

n 1!

2n n 1!

функция y ex

возрастающая, то

e0,5

будем

подбирать

из

неравенства

2n n 1!

0,01.

2n n 1!

n 4получим

0,5 2

0,5 3

0,5 4

При

0,01, значит,

e 1 0,5

24 4 1!

4 120

заданной точностью

e 1,5 0,125 0,02083 0,0026 1,65

Пример 2: Вычислить sin0,1с точностью 0,000001

Решение: sin x x 31!x3 51!x5 ...

sin0,1 0,1 31! 0,1 3 51! 0,1 5 ...

Заметим, что в знакочередующемся ряду остаток ряда по модулю не превосходит его первого слагаемого (этот факт отмечался в доказательстве признака Лейбница сходимости рядов).

1	5	1				1
	0,1						0,000001, поэтому
5!		120 105			12000000
sin0,1 0,1			1	0,1 3		0,1 0,00017 0,09983

		3!

Пример 3: вычислить интеграл

0,1sin x

с точностью 0,001.

Решение: Поскольку sin x x

x5 ..., то

sin x

...

0,1sin x

0,1

0 x

... dx

600

...

0,1 0,1 3 0,1 5 ...

18 600

В этом знакочередующемся ряду уже второе слагаемое по модулю меньше, чем 0,001,

поэтому 0,1sin x 0,1

0 x

Приближенные вычисления с помощью формулы Тейлора

Пример 1: вычислить

e с точностью 0,01

Решение: поскольку

e0,5

и ex

, то

n 0 n!

1 0,5

0,5 2

0,5 3

...

0,5 n

r x . Нужно подобрать число n так, чтобы

f n 1 c

rn x

x x0 n

0,5 0 n

0,01

, где c 0;0,5 . Поскольку

n 1!

2n n 1!

функция y ex

возрастающая, то

e0,5

будем

подбирать

из

неравенства

2n n 1!

0,01.

2n n 1!

При n 4получим

0,5 2

0,5 3

0,5 4

0,01, значит,

e 1 0,5

24 4 1!

4 120

заданной точностью

e 1,5 0,125 0,02083 0,0026 1,65

Пример 2: Вычислить sin0,1с точностью 0,000001

Решение: sin x x 31!x3 51!x5 ...

sin0,1 0,1 31! 0,1 3 51! 0,1 5 ...

1	5	1				1
	0,1						0,000001, поэтому
5!		120 105			12000000
sin0,1 0,1			1	0,1 3		0,1 0,00017 0,09983

		3!

Пример 3: вычислить интеграл

0,1sin x

с точностью 0,001.

Решение: Поскольку sin x x

x5 ..., то

sin x

...

0,1sin x

0,1

... dx

...

0 x

600

0,1 0,1 3 0,1 5 ...

18 600

В этом знакочередующемся ряду уже второе слагаемое по модулю меньше, чем 0,001,

поэтому 0,1sin x 0,1

0 x

Соседние файлы в папке Лекции

#
06.10.2022849.72 Кб20Лекция 1. Числовые ряды.pdf
#
06.10.2022686 Кб23Лекция 2. Функциональные ряды..pdf
#
06.10.2022189.67 Кб22Лекция 3. Комплексные числа.pdf
#
06.10.2022602.5 Кб24Лекция 4. Дифференциальные уравнения первого порядка.pdf
#
06.10.2022616.21 Кб22Лекция 5. Дифференциальные уравнения первого порядка _ продолжение.pdf
#
06.10.2022711.88 Кб23Лекция 6. Дифференциальные уравнения высших порядков, допускающие понижение порядка.pdf
#
06.10.2022584.05 Кб27Лекция 7. Линейные однородные дифференциальные уравнения с постоянными коэффициентами.pdf