Добавил:

menson13 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Томский Государственный Университет Систем Управления и Радиоэлектроники

Предмет:

Математический анализ

Файл:

glv_2

.pdf

Скачиваний:

Добавлен:

28.09.2022

Размер:

954.28 Кб

Скачать

☆

1 / 41 2 3 4 > Следующая >>>

PROIZWOLXNYM OBRAZOM NA

g L A W A 2. opredel>nnyj integral

2.1. pONQTIE I SWOJSTWA

2.1.1. pONQTIE OPREDELENNOGO INTEGRALA

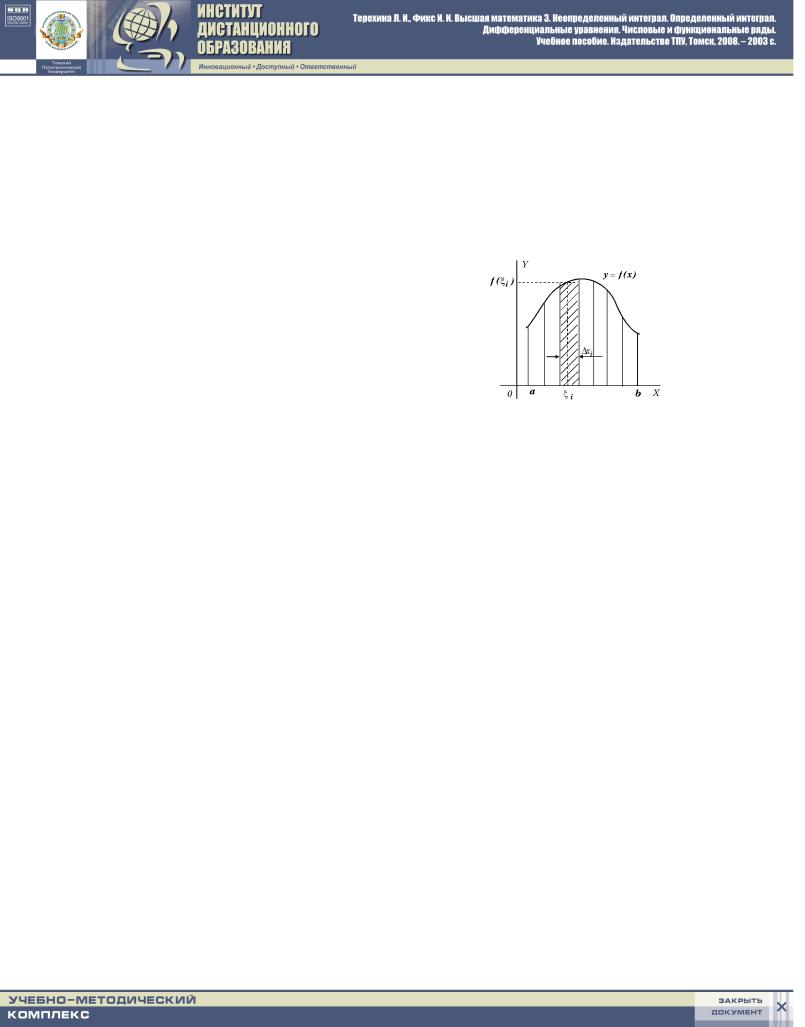
pUSTX W PROMEVUTKE [ a b ] ZADANA NEPRERYWNAQ FUNKCIQ y = f(x):

1.	rAZOBXEM PROMEVUTOK	[ a b ]
^ASTEJ S DLINAMI xi (i = 1		2 : : : n):
2.	w KAVDOM ^ASTI^NOM PROMEVUTKE WYBEREM TO^KU i

LIM ZNA^ENIQ FUNKCII y = f(x) W KAVDOJ IZ \TIH TO^EK. ZNA^ENIQ

I WY^IS- pOLU^IM

f( 1)	f( 2) f( 3) : : : f( n):
3. \|TI ZNA^ENIQ f( i)	UMNOVIM NA DLINY SOOTWETSTWU@]IH ^AS-

TI^NYH PROMEVUTKOW xi A POLU^ENNYE PROIZWEDENIQ f( i) xi SLOVIM. pOLU^ITSQ SUMMA

f( 1) x1 + f( 2) x2 + : : : + f( n) xn = X f( i) xi

i=1

KOTORAQ NAZYWAETSQ INTEGRALXNOJ SUMMOJ FUNKCII y = f(x) W DAN- NOM PROMEVUTKE.

o P R E D E L E N I E. oPREDELENNYM INTEGRALOM OT FUNKCII y = f(x) W INTERWALE [a b] NAZYWAETSQ KONE^NYJ PREDEL SOOTWETSTWU@]EJ INTEG- RALXNOJ SUMMY PRI NEOGRANI^ENNOM UWELI^ENII ^ISLA RAZBIENIJ PRO-

MEVUTKA NA ^ASTI (n			! 1)	I STREMLENII DLIN WSEH ^ASTI^NYH
PROMEVUTKOW K NUL@		( xi ! 0)		I OBOZNA^AETSQ SIMWOLOM
		( xi ! 0)
		b			n
	aZ				n
		f(x) dx = lim				f( i) xi:
				n!1 i=1
					X

tEOREMA SU]ESTWOWANIQ OPREDELENNOGO INTEGRALA. eSLI FUNKCIQ f(x)

QWLQETSQ NEPRERYWNOJ ILI KUSO^NO-NEPRERYWNOJ W INTERWALE [ a b ] (T.E. IMEET W \TOM INTERWALE KONE^NOE ^ISLO TO^EK RAZRYWA 1-GO RODA), TO OPREDELENNYJ INTEGRAL OT \TOJ FUNKCII W \TOM PROME- VUTKE WSEGDA SU]ESTWUET.

pRI WYPOLNENII \TIH USLOWIJ OPREDELENNYJ INTEGRAL NE ZAWISIT NI OT WYBORA TO^EK i NI OT SPOSOBA RAZBIENIQ PROMEVUTKA NA ^ASTI. eSLI OPREDELENNYJ INTEGRAL OT FUNKCII SU]ESTWUET, T.E. SU- ]ESTWUET KONE^NYJ PREDEL SOOTWETSTWU@]EJ INTEGRALXNOJ SUMMY, TO FUNKCIQ NAZYWAETSQ INTEGRIRUEMOJ W \TOM PROMEVUTKE. oTME- TIM, ^TO MONOTONNAQ OGRANI^ENNAQ FUNKCIQ WSEGDA INTEGRIRUEMA.

gEOMETRI^ESKIJ SMYSL OPREDELENNOGO INTEGRALA oPREDEL<NNYJ INTEGRAL OT NEOTRICATELX-

NOJ W PROMEVUTKE FUNKCII UDOBNO TRAKTO- WATX KAK PLO]ADX KRIWOLINEJNOJ TRAPECII, OGRANI^ENNOJ SWERHU GRAFIKOM \TOJ FUNK-

CII, SNIZU OSX@	OX	SLEWA I SPRAWA PRQ-
MYMI x = a	x = b	PARALLELXNYMI OSI
OY .

wELI^INY SLEDU@]IH INTEGRALOW POLU^ENY NA OSNOWANII IH GEOMET- RI^ESKOGO SMYSLA

Z5(x ; 1) dx = 8			(PLO]ADX PRQMOUGOLXNOGO TREUGOLXNIKA, OGRANI-
1
^ENNOGO PRQMYMI y = x				;	1 x = 1 x = 5 I OSX@ OX).
2				;
Z p			(PLO]ADX POLUKRUGA y = +p				RADIUSA 2).
Z p	4 ; x2	dx = 2	(PLO]ADX POLUKRUGA y = +p			4 ; x2	RADIUSA 2).

2.1.2. CWOJSTWA OPREDELENNOGO INTEGRALA

1. pO^LENNOE INTEGRIROWANIE.

oPREDELENNYJ INTEGRAL OT ALGEBRAI^ESKOJ SUMMY FUNKCIJ RAWEN ALGEBRAI^ESKOJ SUMME INTEGRALOW OT SLAGAEMYH

b	b	b
aZ	[f(x) g(x)] dx = Za	f(x) dx aZ g(x)dx:

2. wYNESENIE POSTOQNNOGO MNOVITELQ .

pOSTOQNNYJ MNOVITELX WYNOSITSQ ZA ZNAK OPREDELENNOGO INTEGRALA

b	b
Za	k f(x) dx = k Za	f(x) dx:

sWOJSTWA 1 I 2 POWTORQ@T SWOJSTWA NEOPREDELENNOGO INTEGRALA I ISPOLXZU@TSQ NEPOSREDSTWENNO PRI WY^ISLENIQH.

3. rAZBIENIE OTREZKA INTEGRIROWANIQ NA ^ASTI.

eSLI PROMEVUTOK INTEGRIROWANIQ [a b]		RAZBIT TO^KOJ c NA ^ASTI,
TO OPREDELENNYJ INTEGRAL MOVNO PREDSTAWITX W WIDE SUMMY INTEG-
RALOW PO OTDELXNYM ^ASTQM PROMEVUTKA
Zb f(x) dx = Zc f(x) dx + Zb f(x) dx:
a	a	c

sWOJSTWO 3 ISPOLXZUETSQ, W OSNOWNOM, PRI WY^ISLENIQH S POMO]X@ OPREDELENNOGO INTEG- RALA PLO]ADEJ FIGUR, OB_EMOW TEL, DLIN DUG I T.D.

4. sMENA NAPRAWLENIQ INTEGRIROWANIQ.

pRI PEREMENE MESTAMI PREDELOW INTEGRIROWANIQ OPREDELENNYJ IN- TEGRAL MENQET SWOJ ZNAK

Zb f(x) dx = ; Za f(x) dx:
a	b

5. iNTEGRAL PO PROMEVUTKU NULEWOJ DLINY.

iNTEGRAL S RAWNYMI PREDELAMI INTEGRIROWANIQ RAWEN NUL@

Za f(x) dx = 0:

6. iNTEGRAL OT NE^ETNOJ I ^ETNOJ FUNKCIJ W SIMMETRI^NOM INTERWALE. oPREDELENNYJ INTEGRAL W SIMMETRI^NYH PREDELAH OT NE^ETNOJ FUNK- CII RAWEN NUL@.

	eSLI f(x) = ;f(;x)	TO Za f(x) dx = 0:
		;a
pRI \TOM, DLQ ^ETNOJ FUNKCII ( f(x) = f(;x) ) IMEEM
	Za f(x) dx = 2 Za f(x) dx:
sWOJSTWO 6	;a	0
	I GEOMETRI^ESKIJ SMYSL INTEGRALA MOGUT BYTX \FFEKTIWNO ISPOLXZOWANY W

PODHODQ]IH DLQ \TOGO SLU^AQH.

nAPRIMER, WSE SLEDU@]IE INTEGRALY RAWNY NUL@, TAK KAK PODYN- TEGRALXNYE FUNKCII NE^ETNYE, A PROMEVUTOK INTEGRIROWANIQ SIM- METRI^EN

=2	2		x3		3	sin x
Z x2 sin3 x dx = 0	Z				Z
				dx = 0			dx = 0:
						x4 + x2 + 1
			(1 + 3x2)3
; =2	;2	q			;3

7. O ZNAKE INTEGRALA.

							b
	eSLI f(x) 0 DLQ WSEH			x 2 [a b]	TO		aZ	f(x) dx 0:
8. iNTEGRIROWANIE POD ZNAKOM NERAWENSTWA.
eSLI f(x) g(x) DLQ WSEH			x 2 [a b] TO			Zb f(x) dx Zb g(x) dx:
						a		a
9. oCENKA OPREDELENNOGO INTEGRALA.
1)	mODULX INTEGRALA NE BOLX[E INTEGRALA OT MODULQ FUNKCII
	b			b
	Za	f(x) dx		Za j f(x) j dx:
2)	eSLI f(x) { NEPRERYWNAQ		W INTERWALE		[a	b]	FUNKCIQ I m;		NAI-
MENX[EE, A M; NAIBOLX[EE ZNA^ENIQ FUNKCII								W DANNOM INTER-
WALE, TO
			b
	m (b ; a) Za			f(x) dx M (b ; a):

sWOJSTWO 9 MOVET BYTX ISPOLXZOWANO DLQ OCENKI WELI^INY TRUDNO WY^ISLQEMOGO OPRE- DELENNOGO INTEGRALA.

oCENITX WELI^INU INTEGRALA

Z px4 ; 8x2 + 17 dx:

f0(x) = 1

4x3 ; 16x

= 0

PRI x =

;

2 x = 0 x

= 2:

4 q(x4 ; 8x2 + 17)3

tO^KA x = ;2 NE PRINADLEVIT DANNOMU PROMEVUTKU. iMEEM

f( 1) = p10

f(0) = p17

f(2) = p1 = 1;= fNAIM: f(3) = p26 2 25 = fNAIB::

dLINA PROMEVUTKA (b ; a) = 3

; (;1) = 4 (b ; a)m = 4 1 = 4

(b ; a)M = 4

2 25 = 9: tOGDA

; 8x2 + 17 dx 9:

4 Z px4

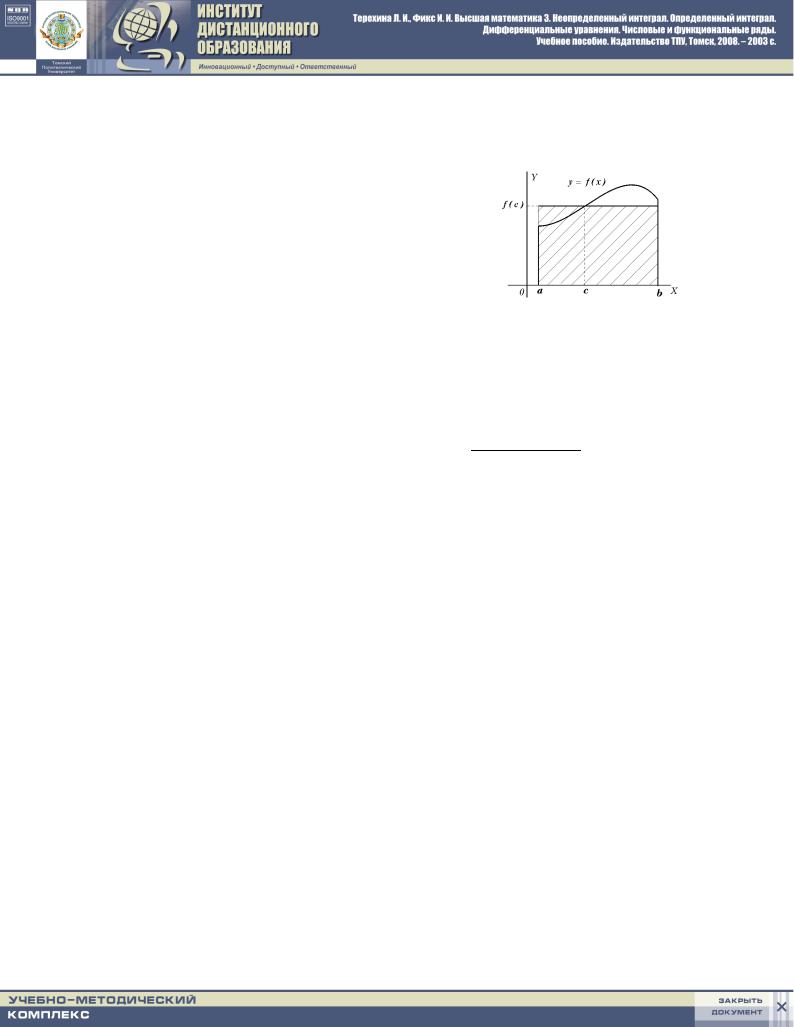
10. tEOREMA O SREDNEM DLQ OPREDELENNOGO INTEGRALA:

eSLI FUNKCIQ y = f(x) NEPRERYWNA W PROMEVUTKE [a b], TO

Zb f(x)dx = f(c)(b ; a) GDE (b ; a){ DLINA OTREZKA, A c 2 (a b):

w GEOMETRI^ESKOM SMYSLE TEOREMA O SREDNEM OZNA^AET, ^TO PLO]ADX KRIWOLINEJNOJ TRA- PECII RAWNA PLO]ADI PRQMOUGOLXNIKA S TEM VE OSNOWANIEM I WYSOTOJ, RAWNOJ ZNA^ENI@ PODYNTEGRALXNOJ FUNKCII W NEKOTOROJ TO^KE c PROMEVUTKA INTEGRIROWANIQ.

wELI^INA f(c) PRI \TOM NAZYWAETSQ SREDNIM ZNA^ENIEM INTERWALE I WY^ISLQETSQ SOOTWETSTWENNO PO FORMULE

		1	b
	fSR:ZN: = f(c) =	1	aZ	f(x)dx:
	fSR:ZN: = f(c) =	b ; a	aZ	f(x)dx:
					p	dx
	nAJTI SREDNEE ZNA^ENIE FUNKCII y =						; p
						x + 9
						x + 9		x
WALE [0 16]:

FUNKCII W

W INTER-

sOGLASNO FORMULE DLQ SREDNEGO ZNA^ENIQ FUNKCII NAHODIM

fSR:ZN: = f(c) =

f(x)dx =

0 75:

;

x + 9

;

zDESX NE PRIWEDENO SAMO WY^ISLENIE INTEGRALA, TAK KAK METODY WY^ISLENIQ OPREDE- LENNYH INTEGRALOW PRIWODQTSQ NIVE.

iNTEGRAL S PEREMENNYM WERHNIM PREDELOM

iNTEGRALOM S PEREMENNYM WERHNIM PREDELOM NAZYWAETSQ INTEGRAL Zx f(t) dt = (x) KOTORYJ QWLQETSQ FUNKCIEJ WERHNEGO PREDELA.

t E O R E M A bARROU. pROIZWODNAQ INTEGRALA S PEREMENNYM WERHNIM PREDELOM RAWNA ZNA^ENI@ PODYNTEGRALXNOJ FUNKCII NA \TOM PREDELE

0Zx f(t) dt10 = f(x):

@a Ax

iZ \TOJ TEOREMY WYTEKAET ODNO WAVNOE SLEDSTWIE. iNTEGRAL S PERE-

MENNYM WERHNIM PREDELOM QWLQETSQ PERWOOBRAZNOJ DLQ PODYNTEG-

RALXNOJ FUNKCII. |TO SLEDSTWIE POZWOLQET WYWESTI OSNOWNU@ FOR- MULU INTEGRALXNOGO IS^ISLENIQ { FORMULU nX@TONA-lEJBNICA.

2.1.3. fORMULA nX@TONA {lEJBNICA

wY^ISLENIE OPREDELENNOGO INTEGRALA, SLEDUQ EGO OPREDELENI@, KAK PREDELA INTEGRALXNOJ SUMMY WESXMA TRUDNAQ I GROMOZDKAQ OPE- RACIQ. sU]ESTWUET BOLEE LEGKIJ PUTX WY^ISLENIQ, OSNOWANNYJ NA PRIMENENII SLEDU@]EJ TEOREMY.

t E O R E M A. wELI^INA OPREDELENNOGO INTEGRALA RAWNA RAZNOSTI ZNA^ENIJ L@BOJ PERWOOBRAZNOJ OT PODYNTEGRALXNOJ FUNKCII, WZQTYH PRI NIVNEM I WERHNEM PREDELAH INTEGRIROWANIQ

tAKIM OBRAZOM, ESLI F(x) ESTX KAKAQ-LIBO PERWOOBRAZNAQ DLQ FUNK- CII f(x), TO SPRAWEDLIWO RAWENSTWO

b		b
aZ	f(x) dx = F (x)	a	= F (b) ; F(a):
	f(x) dx = F (x)		= F (b) ; F(a):

|TA FORMULA NAZYWAETSQ FORMULOJ nX@TONA-lEJBNICA.

wWEDENNAQ FORMULA POZWOLQET TEPERX SFORMULIROWATX NE TOLXKO RAZ- LI^IE, NO I SHODSTWO NEOPREDELENNOGO I OPREDELENNOGO INTEGRALOW.

r A Z L I ^ I Q.

nEOPREDELENNYJ INTEGRAL ESTX SEMEJSTWO PERWOOBRAZNYH FUNKCIJ F (x) + C I W GEOMETRI^ESKOM SMYSLE ESTX SEMEJSTWO INTEGRALXNYH LINIJ { GRAFIKOW WSEH PERWOOBRAZNYH FUNKCIJ, POLU^A@]IHSQ PRI NEPRERYWNOM PARALLELXNOM PEREME]ENII L@BOJ IZ NIH PO WERTIKA- LI.

oPREDELENNYJ INTEGRAL ESTX KONKRETNOE ^ISLO, KOTOROE S GEOMET- RI^ESKOJ TO^KI ZRENIQ UDOBNO TRAKTOWATX KAK PLO]ADX SOOTWETSTWU- @]EJ KRIWOLINEJNOJ TRAPECII.

s H O D S T W O (SWQZX).

nESMOTRQ NA RAZLI^NU@ PRIRODU NEOPREDELENNOGO I OPREDELENNOGO INTEGRALOW, MEVDU NIMI ESTX MNOGO OB]EGO. |TO KASAETSQ NE TOLX- KO WNE[NEGO SHODSTWA, NO I SWOJSTW \TIH INTEGRALOW I METODOW IH WY^ISLENIQ. kROME \TOGO, WSQKIJ OPREDELENNYJ INTEGRAL, SOGLASNO FORMULE nX@TONA{lEJBNICA, ESTX PRIRA]ENIE PERWOOBRAZNOJ FUNK- CII NA OTREZKE [a b] : F = F (b) ; F(a):

2.2. wY^ISLENIE OPREDELENNOGO INTEGRALA

fORMULA nX@TONA{lEJBNICA, SWQZYWA@]AQ WY^ISLENIQ OPREDELEN- NOGO I NEOPREDELENNOGO INTEGRALOW, POZWOLQET SDELATX WYWOD, ^TO WSE METODY NEOPREDELENNOGO INTEGRIROWANIQ MOVNO S OPREDELENNY- MI OGOWORKAMI PERENESTI NA SLU^AJ OPREDELENNOGO INTEGRIROWANIQ.

2.2.1. nEPOSREDSTWENNOE INTEGRIROWANIE

k \TOMU METODU MY OTNESLI TAKIE INTEGRALY, PRI RE[ENII KO- TORYH ISPOLXZU@TSQ TABLICY NEOPREDELENNYH INTEGRALOW I PODWEDE- NIQ POD ZNAK DIFFERENCIALA, SWOJSTWA INTEGRALOW I FORMULA nX@TONA- lEJBNICA, SOGLASNO KOTOROJ MY SNA^ALA NAHODIM PERWOOBRAZNU@ FUNK- CI@, A ZATEM WY^ISLQEM RAZNOSTX EE ZNA^ENIJ W WERHNEM I NIVNEM PREDELAH INTEGRIROWANIQ. rASSMOTRIM PRIMERY.

1: Z p

3 ; 5p

dx = Z

; 5p

dx =

= Z1

3x1=3 ; 5x5=6

= 3 Z1 x1=3 dx ; 5 Z1 x5=6 dx =

xn+1

x4=30 1

x11=6 10

= Z xn dx =

= 3 4=3 0 ; 511=6

0 =

4 x4=3

;

11 x11=6

0 =

n + 1

;

(1 ; 0) ;

11(1 ; 0) = 4

= ;44 ;0 48:

;1 d (5x + 11)

;

(11 + 5x)2

1;2

1 1

= ;

2 = ;5

;

! = ;

; 1! =

5 11 + 5x

;

5 6

(1 + ex)

; ex

dx =

1 + ex

;

1 + ex !

1 + ex

(ex + 1)

Z dx = x

= Z dx ; Z

1 + ex

= ln U

;1 1

= x

;

1 ; ln j 1 + ex j

;

1 = 1 ; (;1) ;

ln j 1 + e j ; ln j 1 + e;1 j =

1 + e

(1 + e)e

= 2 ; ln

= 2

; ln

= 2 ; ln e = 2 ; 1 = 1:

1 + 1=e

e + 1

px + 9 + px

x + 9

(

px)

;

x + 9 + px) ( x + 9

;

16 p

x + 9 + px

16 p

Z (

dx =

x + 9 + px

dx =

(px)

x + 9

;

x + 9)

;

(px + 9 + px) dx =

9 Z

+ 9)3=2 + x3=2

253=2

;

93=2

+ 163=2

;

+ 43

= 2

2 5:

2.2.2. iNTEGRIROWANIE PO ^ASTQM

iNTEGRIROWANIE PO ^ASTQM W OPREDELENNOM INTEGRALE PROWODITSQ PO FORMULE

U dV = U V

a ;

V dU.

U = x

dU = dx

5: Z1 x 32x dx =

dx V = Z 3

dV = 3

dx = 2 ln 3

Z 32x

= x

32x j0 ;

dx =

32x j0

;

32x

2 ln 3

4 ln2 3

9 ln 3

; 4

64:

;

4 ln2 3

;

; 4 ln2

2 ln 3

2 ln2

U = arcsin px

1=4 arcsin p

dU =

1 ; x

;

dx =

dV = p dx

V = 2p

1 x

;

1=4

1 ; x

= ;2p1 ; x arcsin px j01=4 + Z

2p1

; x

1 x

1=4

1=4 dx

1=4

= ;2

1 ; x arcsin

x j0

+ Z

px = ;2

1;x arcsin

xj0

= ;2q

arcsin(1=2) ; 0 + 2(1=2) ; 0 = ;p

6 + 1 0 1:

3=4

2.2.3. zAMENA PEREMENNOJ. pODSTANOWKA

pRAWILO ZAMENY PEREMENNOJ W OPREDELENNOM INTEGRALE TREBUET K SEBE ZNA^ITELXNO BOLX[EGO WNIMANIQ, ^EM ANALOGI^NOE PRAWILO W NEOPREDELENNOM INTEGRALE. sFORMULIRUEM EGO.

pRAWILO ZAMENY PEREMENNOJ W OPREDELENNOM INTEGRALE.

eSLI FUNKCIQ f(x) NEPRERYWNA W INTERWALE [a b], A FUNKCIQ '(t) MO- NOTONNA I NEPRERYWNA WMESTE SO SWOEJ PROIZWODNOJ W INTERWALE [ ], PRI^EM '( ) = a '( ) = b, TO IMEET MESTO FORMULA

b
Za	f(x) dx = Z f [ (' (t) ] '0(t) dt:

|TA FORMULA I NAZYWAETSQ FORMULOJ PODSTANOWKI ILI ZAMENY PERE- MENNOJ W OPREDELENNOM INTEGRALE.

sHEMA PRIMENENIQ SPOSOBA PODSTANOWKI DLQ WY^ISLENIQ INTEGRALA WYGLQDIT SLEDU@]IM OBRAZOM.

1) wYBRATX PODSTANOWKU (SDELATX ZAMENU PEREMENNOJ)

x = '(t) TAK ^TOBY FUNKCIQ '(t) BYLA NEPRERYWNOJ I MONOTONNOJ W INTERWALE [ ]:

2)nAJTI dx = '0(t) dt PRI^EM PROIZWODNAQ '0(t) TAKVE DOLVNA BYTX NEPRERYWNOJ FUNKCIEJ.

3)pODYNTEGRALXNU@ FUNKCI@ f(x) PREOBRAZOWATX S U^ETOM WY- BRANNOJ PODSTANOWKI.

4)sMENITX PREDELY INTEGRIROWANIQ, T.E. W SOOTWETSTWII S PRO-

IZWEDENNOJ ZAMENOJ NAJTI ZNA^ENIQ PEREMENNOJ	t:	t1	=	I
t2 = SOOTWETSTWU@]IE ZNA^ENIQM PEREMENNOJ	x:	x1	= a	I
x2 = b:

5) pODSTAWITX WSE W ISHODNYJ INTEGRAL I WY^ISLITX EGO.

iTAK, SHEMA DEJSTWIJ PRI ZAMENE PEREMENNOJ W OPREDELENNOM IN- TEGRALE TA VE, ^TO I W NEOPREDELENNOM. rAZNICA SOSTOIT LI[X W TOM, ^TO POSLE WYPOLNENENIQ INTEGRIROWANIQ NE NUVNO WOZWRA]ATXSQ K STAROJ PEREMENNOJ x A WY^ISLENIQ PROWODITX DLQ PEREMENNOJ t W INTERWALE [ ]:

x = sin t

x p

dx = cos t dt

x2 = cos t

1=2

;

cos t dt

= Z

= ln

sin t

cos t

sin t

= t

3x + 1

3x + 1 = t2

8: Z

2x + p

= x =

(t2

;

3x + 1

dx =

t dt

= Z

(t2

;

1) + t

t2 +

;

t = arcsin x

= 1=2

)

t1 = =6

= =3

x2 = 3=2 ) t2

= ln

; ln

= ln 0 577

; ln 0 268 0 77:

t = p

3x + 1

x1 = 0

t1 = 1

x2 = 5

t2 = 4

pOLU^ILI INTEGRAL S KWADRATNYM TREH^LENOM W ZNAMENATELE. nE BUDEM PRIWODITX PODROBNYH WYKLADOK, ZAPI[EM OKON^ATELXNYJ RE- ZULXTAT

1=2

ln j t2 +

t ; 1 j 1 ;

t;+ 2

7=2

1=2

2 3

ln 21

;

6 ;

3 ; 10

2! ; 10 0

3 1

ln 14 ;

0 94:

tg 2

= t

t = tg

x = 2 arctg t

x1 = 0

t1 = 0

2 dt

dx =

x2 = =2

t2 = 1

2 + cos x

1 + t

cos x =

; t22

2 dt

1 + t

= Z

= 2

= p3

arctgp3

2 +

1;t2

1 + t2

3 + t2

1+t

= p

arctgp

; arctg 0! =

0 6:

1 / 41 2 3 4 > Следующая >>>

Соседние файлы в предмете Математический анализ

#
28.09.20221.01 Mб4glv_1.pdf
#
28.09.2022954.28 Кб2glv_2.pdf
#
28.09.2022136.73 Кб3Таблица интегралов.pdf
#
28.09.202268.01 Кб2Таблица производных.pdf
#
28.09.20222.22 Mб9Терехина Фикс ВМ 2.PDF