Добавил:

menson13 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Томский Государственный Университет Систем Управления и Радиоэлектроники

Предмет:

Математический анализ

Файл:

glv_2

.pdf

Скачиваний:

Добавлен:

28.09.2022

Размер:

954.28 Кб

Скачать

☆

<<< < Предыдущая 1 23 / 43 4 > Следующая >>>

2.4. pRILOVENIQ OPREDELENNOGO INTEGRALA

oPREDELENNYJ INTEGRAL PRIMENQETSQ O^ENX [IROKO W GEOMETRII, FI- ZIKE, HIMII, ESTESTWOZNANII.

2.4.1. oB]AQ SHEMA PRIMENENIQ INTEGRALA

rE[ENIE L@BOJ ZADA^I GEOMETRII, HIMII ILI FIZIKI, KOTORAQ SWED<TSQ, W KONE^NOM S^<TE, K WY^ISLENI@ INTEGRALA, DOLVNO, STROGO GOWORQ, OSU]ESTWLQTXSQ PO STANDART- NOJ SHEME. |TA SHEMA POWTORQET SHEMU POSTROENIQ OPREDEL<NNOGO INTEGRALA, T.E. DELENIE PROMEVUTKA NA ^ASTI, WYBOR TO^EK W PREDELAH KAVDOGO ^ASTI^NOGO PROMEVUTKA, SOSTAW- LENIe INTEGRALXNOJ SUMMY, PEREHOD K PREDELU. oDNAKO, PRI RE[ENII ZADA^, KAVDYJ RAZ \TU POLNU@ SHEMU POWTORQTX NET NEOBHODIMOSTI. dOSTATO^NO WYPOLNITX PRAWILXNO LI[X ODNO ZWENO \TOJ SHEMY { SOSTAWITX WYRAVENIE DLQ OB]EGO ^LENA INTEGRALXNOJ SUMMY. zADA^A RE[AETSQ PO SLEDU@]EJ UPRO]ENNOJ SHEME.

pUSTX TREBUETSQ OPREDELITX NEKOTORU@ WELI^INU Q (PLO]ADX FIGURY, DLINA DUGI, RABOTA SILY, KOLI^ESTWO TEPLA, KINETI^ESKAQ \NERGIQ I T.D.), SWQZANNU@ S PROMEVUTKOM

x2 [a b].

1)wYDELQEM \LEMENT Q ISKOMOJ WELI^INY Q, SOOTWETSTWU@]IJ \LEMENTARNOMU PROMEVUTKU x.

2)sOSTAWLQEM PRIBLIV<NNOE RAWENSTWO DLQ \LEMENTA WELI^INY

Q ' q(x) x (PRI \TOM ISPOLXZU@TSQ IZWESTNYE GEOMETRI^ESKIE FORMULY, FIZI^ESKIE ZAKONY, SOOTNO[ENIQ I T.D.) KOTOROE NE DOLVNO OTLI^ATXSQ OT TO^NOGO ZNA^ENIQ WELI^I- NY Q BOLEE, ^EM NA BESKONE^NO MALU@ WYS[EGO PORQDKA MALOSTI. dALEE PRIBLIV<NNOE RAWENSTWO MOVNO ZAMENITX TO^NYM W DIFFERENCIALXNOJ FORME dQ = q(x) dx:

3) zNA^ENIE ISKOMOJ WELI^INY Q OPREDELITSQ KAK INTEGRAL OT dQ : Q = Zb q(x) dx: a

2.4.2. nEKOTORYE FIZI^ESKIE ZADA^I

zADA^A 1. tELO DWIVETSQ PRQMOLINEJNO SO SKOROSTX@

v(t) = 3t2	2
v(t) = 3t2	+ t + 1	+ 5 M=SEK nAJTI PUTX, KOTORYJ PROJDET TELO ZA

WREMQ OT t1 = 2c DO t2 = 5c:

r E [ E N I E. tELO DWIVETSQ S PEREMENNOJ SKOROSTX@, PO\TOMU WYDELIM MALYJ PROMEVUTOK WREMENI dt W PREDELAH KOTOROGO MOVNO

S^ITATX SKOROSTX NEIZMENNOJ. tOGDA PROJDENNYJ ZA \TOT PROMEVU-
					2		+ 5! dt:
TOK WREMENI PUTX RAWEN dS = v(t) dt =					3t2 +
TOK WREMENI PUTX RAWEN dS = v(t) dt =					3t2 +	t + 1
wESX PROJDENNYJ PUTX ZA ZADANNYJ INTERWAL WREMENI
t2	5	5	2		+ 5! dt =
S = Z	dS = Z v(t) dt = Z		2
			3t2 +
			3t2 +	t + 1
t1	2	2
= t3 + 2 ln jt + 1j + 5t		5
= t3 + 2 ln jt + 1j + 5t		2	= 114 + 2 ln 2 + 15 130 4 M:
72

I = mr2:

zADA^A 2. nAJTI RABOTU, SOWER[AEMU@ SINUSOIDALXNYM TOKOM

I = I0 sin !t W PROWODNIKE SOPROTIWLENIEM R ZA PERIOD WREMENI OT t1 = 0 DO t2 = 20 =!:

r E [ E N I E . nAPOMNIM: RABOTA, SOWER[AEMAQ POSTOQNNYM TOKOM I W PROWODNIKE SOPROTIWLENIEM R ZA WREMQ t OPREDELQETSQ

A = I2 R t:

w PREDELAH BESKONE^NO MALOGO PROMEVUTKA WREMENI 4t PEREMEN- NYJ TOK MOVNO S^ITATX POSTOQNNYM I, PO\TOMU, DLQ PROIZWOLXNOGO

4t IZ RASSMATRIWAEMOGO WREMENNOGO PROMEVUTKA TOK SOWER[IT \LE-

MENTARNU@ RABOTU

I2(t)R t ILI

dA = I2(t)R dt = I02 sin2 !t

R dt:

tAK KAK WREMQ OT t1 = 0 DO

t2 = 20 =! PREDSTAWLQET SOBOJ WREMQ 10

POLNYH PERIODOW, ILI 20 POLUPERIODOW, W KAVDOM IZ KOTORYH SOWER-

[AETSQ ODNA I TA VE RABOTA, IMEEM OKON^ATELXNO

20 =!

sin 2!t

10 I02

(DV:)

I0 sin !t R dt= 20 I0

2 ;

zADA^A 3.

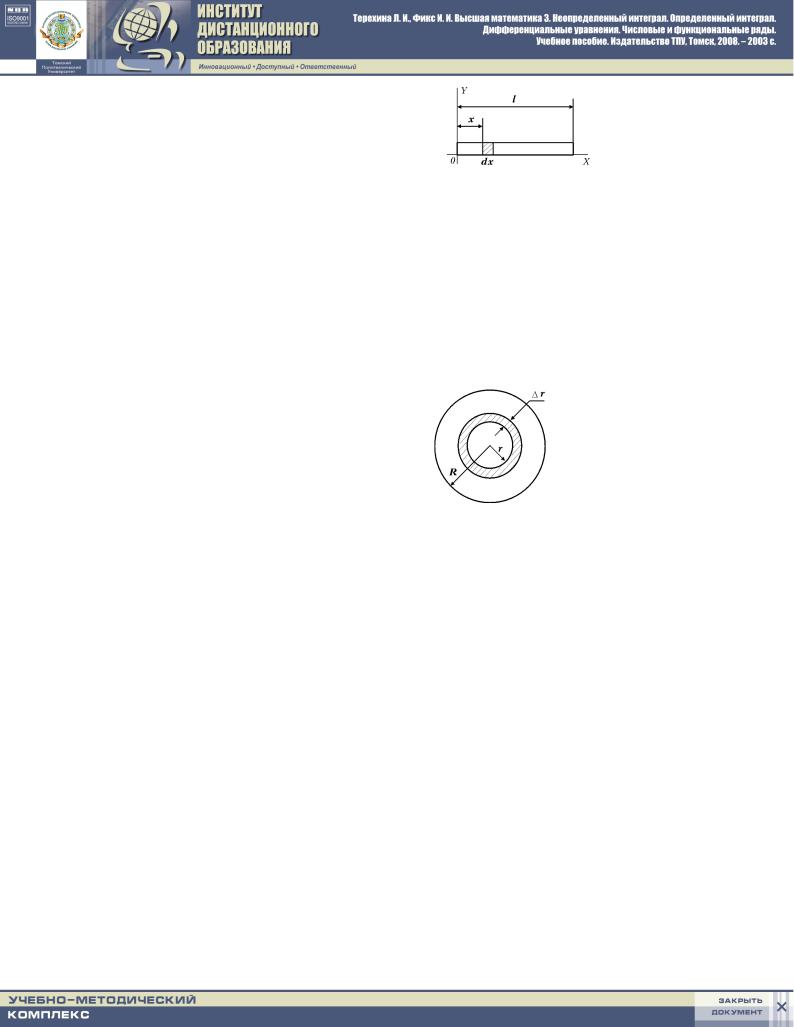
nAJTI MOMENT INERCII ODNORODNOGO STERVNQ MASSOJ M

I DLINOJ l

OTNOSITELXNO ODNOGO IZ EGO KONCOW.

r E [ E N I E . nAPOMNIM: MOMENT INERCII TELA MASSOJ m OT- NOSITELXNO TO^KI ILI OSI, RAWEN PROIZWEDENI@ MASSY TELA NA KWADRAT RASSTOQNIQ OT NEGO DO TO^KI

wYDELIM \LEMENT DLINY STERVNQ 4x, NAHODQ]IJSQ NA RASSTOQNII
x (0 x l) OT EGO LEWOGO KONCA.
tAK KAK STERVENX ODNORODNYJ, TO MASSA EDINICY DLINY (PLOT-
	M
NOSTX) OPREDELITSQ KAK	l TO MASSA WYBRANNOGO \LEMENTA BUDET
RAWNA PROIZWEDENI@ PLOTNOSTI NA DLINU		4m = Ml 4 x:

w SILU MALOSTI U^ASTKA x MOVNO POLAGATX, ^TO RASSTOQNIQ OT NA- ^ALA KOORDINAT DO WSEH TO^EK \TOGO \LEMENTA ODINAKOWY I RAWNY

x: (rIS. 2.5.) tOGDA, ISPOLXZUQ PRIWEDENNU@ FORMULU DLQ MOMEN- TA INERCII, POLU^IM PRIBLIVENNOE RAWENSTWO DLQ MOMENTA INERCII

\LEMENTA x 4I ' 4m x2 = Ml 4 x x2 ILI TO^NOE RAWENSTWO W

DIFFERENCIALAH
		2	M	2		M 2		dx:
dI = dmx			= l	dx x	= l		x	dx:
oKON^ATELXNO IMEEM
I = Z	l M			M x3		l	Ml2
I = Z	l x2		dx =	l 3		0 =	3 :
0
0
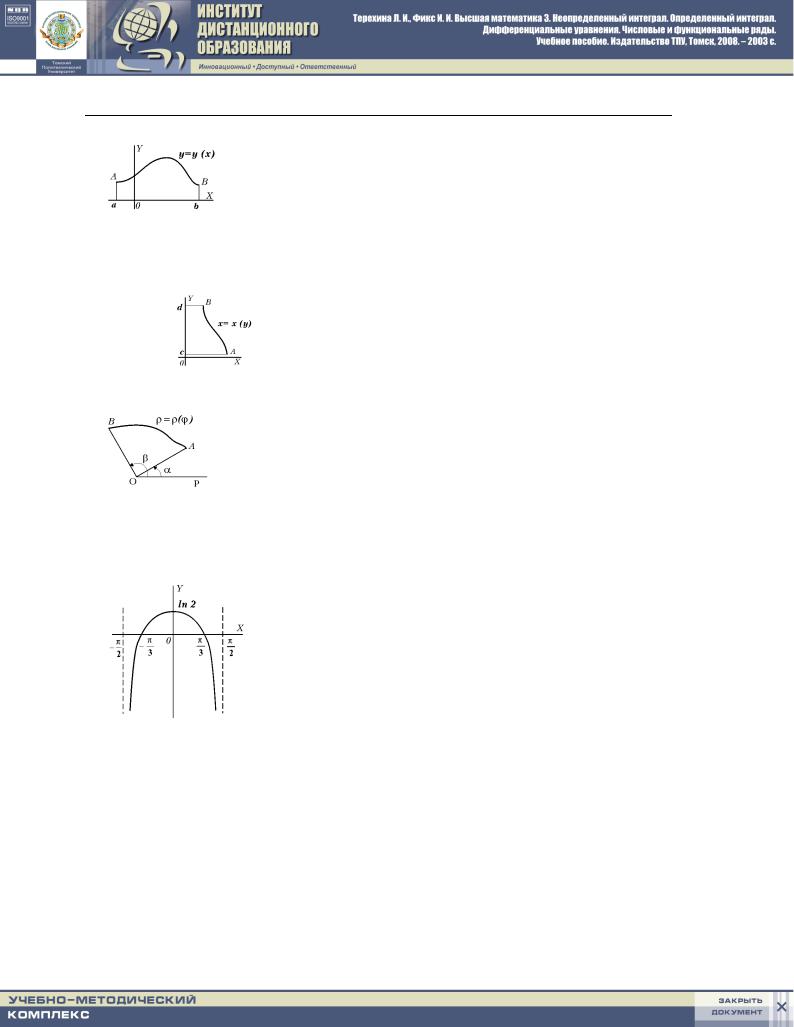
zADA^A 4.			nAJTI KINETI^ESKU@ \NERGI@ ODNORODNOGO DISKA MASSY
M I RADIUSA R, WRA]A@]EGOSQ WOKRUG CENTRALXNOJ OSI S POSTOQNNOJ
SKOROSTX@			!.

r E [ E N I E . nAPOMNIM: KINETI^ESKAQ \NERGIQ MATERIALXNOJ

TO^KI MASSOJ

m, DWIVU]EJSQ SO SKOROSTX@

v RAWNA POLOWINE PROIZ-

WEDENIQ MASSY TO^KI NA KWADRAT E< SKOROSTI

K =

m v2:

wYDELIM \LEMENT DISKA 4S W

WIDE BESKONE^NO UZKOGO KOLX-

[IRINOJ

4r, I RADIU-

SOM

r (0 r R): tAK KAK

MASSA EDINICY PLO]ADI DIS-

KA (POWERHNOSTNAQ PLOTNOSTX)

RAWNA

(KOLXCA)

4S = 2 r 4 r TO MASSA

A PLO]ADX WYBRANNOGO \LEMENTA

\LEMENTA ZAPI[ETSQ 4m =

4 S =

2 r 4 r:

lINEJNU@ SKOROSTX WSEH TO^EK KOLXCA MOVNO S^ITATX ODINAKOWOJ W

SILU MALOSTI WELI^INY

4r I RAWNOJ v(r) = ! r:

kINETI^ESKAQ \NERGIQ \LEMENTA

1 M

M!2

4K ' 2 4 m v

(r) =

2 r 4 r (! r)

4 r ILI

1 M

M!2

dK =

2 dm v

(r) =

2 r dr (! r)

dr:

oKON^ATELXNO POLU^IM

R M!2

M!2 r4 R

K = Z

r3 dr =

R2 4 0

4M!2R2:

zADA^A 5.

wY^ISLITX RABOTU, KOTORAQ BYLA ZATRA^ENA NA POSTROJKU PIRAMIDY hEOPSA. (pIRAMIDA hEOPSA { PRAWILXNAQ ^ETYREHUGOLX-

NAQ PIRAMIDA, STORONA OSNOWANIQ 200M WYSOTA 140M UDELXNYJ WES KAMNQ = 2:5MT3 ).

r E [ E N I E. w ZADA^E TREBUETSQ OPREDELITX RABOTU, ZATRA^EN- NU@ NA PREODOLENIE SILY TQVESTI. wYDELIM SLOJ TOL]INOJ dx NA WYSOTE x OT OSNOWANIQ. w KA^ESTWE \LEMENTA RABOTY PRIMEM RABOTU, KOTORAQ BYLA ZATRA^ENA NA WOZWEDENIE \TOGO SLOQ. oNA WY^ISLQETSQ KAK PROIZWEDENIE WESA \TOGO SLOQ dP = dV (GDE dV ={ OB_EM

\TOGO SLOQ,) NA WYSOTU x NA KOTORU@ EGO NUVNO BYLO PODNQTX dA = dP x = dV x:

tAK KAK OB_EM SLOQ dV = S(x) dx TO

dA = S(x) dx x = x S(x) dx: nEOBHODIMO TEPERX WYRAZITX PLO- ]ADX SLOQ S(x) KAK FUNKCI@ RAS- STOQNIQ x OT OSNOWANIQ PIRAMIDY DO \TOGO SLOQ.

kAK IZWESTNO IZ GEOMETRII, PLO]ADI PARALLELXNYH SE^ENIJ W PIRA- MIDE OTNOSQTSQ KAK KWADRATY IH RASSTOQNIJ DO WER[INY

S(x) =

; x)2

)

S(x) =

SOSN:

;

x)2:

oKON^ATELXNO \LEMENT RABOTY PRIMET WID

SOSN:

(H ; x)2

SOSN:

x (H ; x)2 dx:

dA = x

dx =

A = Z dA =

SOSN:

; x)2 dx =

wSQ RABOTA

x (H

SOSN:

0H2

(H2 x ; 2Hx2 + x3) dx =

2 ;

3 x3 +

4 1

SOSN:

;

SOSN: H2:

iTAK

RABOTA

: A =

SOSN: H

wY^ISLIM EE

ISPOLXZUQ ISHODNYE

DANNYE: A =

2 5 104

4 104 M2 1 96 104 M2 = 1 63 1012 dV:

|TA \NERGIQ SOIZMERIMA S \NERGIEJ TOL^KA PRI RAZRU[ITELXNOM ZEM- LETRQSENII.

2.4.3. wY^ISLENIE PLO]ADEJ PLOSKIH FIGUR

nIVE PRIWEDENY FORMULY DLQ WY^ISLENIQ PLO]ADEJ PLOSKIH FIGUR, OHWATYWA@- ]IE PRAKTI^ESKI WSE WOZMOVNYE SITUACII. pRI RE[ENII ZADA^I NEOBHODIMO NARISOWATX FIGURU, SOPOSTAWITX SO SLU^AQMI, UKAZANNYMI W TABLICE I PODOBRATX NUVNU@ FORMULU.

tABLICA 2.1.

b
1.a) S = Za	y(x) dx
1:b) 8 x = x(t)		t2
1:b) 8 x = x(t)		S = y(t) x0(t) dt
< y = y(t)		tZ1
:

2. S = Zb[y2(x) ; y1(x)] dx

d		d
3. S = Zc	x(y) dy	4. S = Zc	[x2(y) ; x1(y)] dy

5: S = 1 Z 2(') d'

	1
6: S =	2 Z [ 22(') ; 12(')] d'

nAJTI PLO]ADX FIGURY,

OGRANI^ENNOJ LINIQMI:

PARABOLOJ

y = 16 ; x2 I PRQMOJ

x + y + 4 = 0.

sTROIM FIGURU. nAILU^[IM OBRAZOM

W DANNOM SLU^AE PODHODIT FORMULA 2

TABLICY 2.1. nAHODIM ABSCISSY TO^EK

PERESE^ENIQ LINIJ

; x = 16

; x2 =)

x2 ;x;20 = 0 =)

= ;4 x2 = 5.

w PREDELAH IZMENENIQ ARGUMENTA

;4 x 5

WERHNEJ GRANICEJ SLU

rIS. 2.8.

VIT

y2(x) = 16

A NIV

; x

NEJ

y1(x) = ;4 ; x.

pLO]ADX FIGURY

S = aZ [y2(x);y1(x)] dx= Z4 h(16;x );(;4;x)i dx=

;

189

= Z (20 ; x2 + x) dx = (20x ; 3

+ 2 )

;

= 180

; 3

= 121 5:

nAJTI PLO]ADX FIGURY, OGRANI^ENNOJ LINIQMI

xy = 2

y = 2x

y = 3:

sTROIM FIGURU. wIDIM, ^TO NAIBO- LEE PODHODIT DLQ RE[ENIQ ZADA^I

FORMULA 4 W TABLICE 2.1.

S = Zd[x2(y) ; x1(y)] dy:

w NA[EM SLU^AE

x2(y) = 2=y x1(y) = y=2 c = 2 d = 3:

(zNA^ENIE	c = 2		POLU^ILI KAK
TO^KU PERESE^ENIQ GRAFIKOW FUNK-
CIJ xy = 2	y = 2x). iTAK,
	3	y	2	y2	3	5		3
S = Z		2	; y! dy = 0	4 ; 2 ln y1	2 =	4	; 2 ln	2	:
	2		@	A

3. nAJTI PLO]ADX PETLI KRIWOJ x = t2 ; 1 y = t3 ; t:

rIS. 2.10.

sTROIM KRIWU@. wIDIM, ^TO FIGURA SIMMET- RI^NA OTNOSITELXNO OSI OX: nAJDEM PLO- ]ADX WERHNEJ POLOWINKI I REZULXTAT UMNO- VIM NA 2. |TO KRIWOLINEJNAQ TRAPECIQ. iZ- MENENI@ x OT ;1 DO 0 SOOTWETSTWUET IZMENENIE PARAMETRA t OT 0 DO ;1:

sLEDOWATELXNO, PLO]ADX, OGRANI^ENNAQ PETLEJ, MOVET BYTX NAJDENA PO FORMULE 1.b) TABLICY 2.1.

S = 2

;1	;1	0	1	1	!=	8
Z(t3;t) (t2;1)0dt= 2	Z(t3;t) 2tdt= ;4 Z(t4;t2)dt= ;4			;3			:
Z(t3;t) (t2;1)0dt= 2	Z(t3;t) 2tdt= ;4 Z(t4;t2)dt= ;4		5	;3		15	:
0	0	;1
nAJTI PLO]ADX FIGURY, OGRANI^ENNOJ \LLIPSOM
	x = a cos t	y = b sin t:

sTROIM FIGURU. w SILU SIMMETRII MOVNO WY^ISLITX PLO]ADX ZA[TRIHOWANNOJ OBLAS- TI, A ZATEM REZULXTAT UMNOVITX NA 4. dLQ WY^ISLENIQ PLO]ADI ISPOLXZUEM FORMULU

		t2
		tZ1
1.b) TABLICY 2.1.	S =	y(t) x0	dt:
		t

w NA[EM PRIMERE

y = b sin t

dt =

;

a sin t dt:

pREDELY IZMENENIQ PEREMENNOJ

NAJDEM IZ USLOWIJ

x = a cos t

PRI

x1 = 0

t1 = =2

PRI

x2 = a t2 = 0:

tOGDA DLQ IZMENENIQ x OT x = 0

DO x = a

PARAMETR t BUDET

IZMENQTXSQ OT

t1 = =2 DO

t2 = 0:

S = y(t) x0

b sin t a sin t dt = 4

a b sin2 t dt =

; Z

sin 2t

! 0

= 4 a b

;

= 4 a b 4 = a b:

iTOG : PLO]ADX FIGURY, OGRANI^ENNOJ \LLIPSOM RAWNA S\L: = a b:

5. nAJTI PLO]ADX FIGURY, OGRANI^ENNOJ KARDIOIDOJ = 1;cos ':

sTROIM LINI@ W POLQRNYH KOORDINATAH. pLO]ADX FIGURY, OGRANI^ENNOJ KARDIOI- DOJ, BUDEM WY^ISLQTX PO FORMULE 5 TABLICY

2.1.

fUNKCIQ (') = 1

; cos ':

pRI OPREDE-

LENII PREDELOW INTEGRIROWANIQ U^TEM SIM-

METRI@ FIGURY. mOVNO WZQTX INTEGRAL PO

' W PREDELAH OT 0 DO I REZULXTAT UDWOITX.

tOGDA PLO]ADX FIGURY

1 '

S =

2 'Z1

2 (') d' = Z (1

;cos ')2 d' = Z (1

;2 cos '+ cos2 ') d' =

1 + cos 2'

cos 2'

= Z 1

; 2 cos ' +

d' =Z

3=2 ; 2 cos ' +

d' =

sin 2'

' ; 2 sin ' +

= 2 :

2.4.4.wY^ISLENIE DLIN DUG PLOSKIH KRIWYH

tABLICA 2.2.

L = Zb

1: y = y(x)

1 + yx02

dx:

2: 8 x = x(t)

L =

tZ1 q

x0t2

+ yt02

dt:

< y = y(t)

x = x(y)

L =

Zc r

1 + xy02

dy:

4: = (')

L =

+ '02 d':

1. nAJTI DLINU LINII y = ln(2 cos x)

MEVDU SOSEDNIMI

TO^KAMI PERESE^ENIQ S OSX@ OX:

nAJDEM

iTAK,

lINIQ ZADANA W DEKARTOWOJ SISTEME KOOR-

DINAT, PO\TOMU ISPOLXZUEM FORMULU 1 TAB-

LICY 2.2. pREDELY INTEGRIROWANIQ - TO^KI

PERESE^ENIQ KRIWOJ S OSX@ OX NAHODIM IZ

USLOWIQ

y = 0

=) ln(2 cos x) = 0

2 cos x = 1

cos x = 1=2

)

x1 =

x2 =

3 :

(

;

2 sin x) =

;

tg x

1+y02

= 1+tg2 x =

2 cos x

cos2 x

L =

1= cos2 x dx =

= ln tg

cos x

;

= ln

tg 12

; ln

tg 6

2 62:

2. nAJTI DLINU ^ASTI ASTROIDY

x = 2 cos3 t

OT ZNA^ENIQ t1 = 0 DO t2 = =2:

< y = 2 sin t

lINIQ ZADANA PARAMETRI^ESKI:

x = x(t)

y = y(t):

dLINU DUGI WY^ISLQEM

PO FORMULE 2 TABLICY 2.2.

L = Zt2 q

xt02 + yt02

(PARAMETR t

DOLVEN MENQTXSQ OT MENX[EGO

ZNA^ENIQ K BOLX[EMU.)

nAJDEM OTDELXNO

;

6 cos2 t sin t

y0 = 6 sin2 t cos t

+y0

= 36 cos

(cos

t sin t+36 sin t cos

t = 36 sin

t cos

t+sin t) =

= 36 sin2 t cos2 t = 9 sin2 2t:

qxt02 + yt02 = p

= 3 j sin 2t j

9 sin2 2t

tAK KAK cos t I sin t POLOVITELXNY W PERWOJ ^ETWERTI, POLU^IM

L= 3 Z

sin 2t dt= ;2

cos 2t

= ;2

(cos ;cos 0) = ;2 (;1;1) = 3:

nAJTI DLINU PERWOGO WITKA SPIRALI aRHIMEDA

= 3':

lINIQ = 3' ZADANA W POLQRNOJ SISTEME KOORDINAT URAWNENIEM WIDA = (') DLINA

DUGI WY^ISLQETSQ PO FORMULE 4 TABLICY 2.2.

L = Z r 2 + 0'2 d':

~TOBY WY^ISLQTX DLINU DUGI, NEOBHODIMO OPREDELITX PREDELY IZMENENIQ UGLA ' SO-

OTWETSTWU@]IE KRAJNIM TO^KAM DUGI.

w RASSMATRIWAEMOJ ZADA^E PERWYJ WITOK SPIRALI SOOTWETSTWUET IZ-

MENENI@ UGLA ' OT 0 DO 2 : nAHODIM

PREDWARITELXNO

q 2

0 = (3')0 = 3

= (3')

+ 3

= 3

1 + ' :

Z q

2 + '02 d' = 3

1 + '2 d':

tOGDA L =

dANNYJ INTEGRAL MOVNO WZQTX IZ TABLICY2 INTEGRALOW

L = 3

' p

' + p

1 + '2

= 3 p1 + 4 2 +

2 + p1 + 4 2

<<< < Предыдущая 1 23 / 43 4 > Следующая >>>

Соседние файлы в предмете Математический анализ

#
28.09.20221.01 Mб4glv_1.pdf
#
28.09.2022954.28 Кб2glv_2.pdf
#
28.09.2022136.73 Кб3Таблица интегралов.pdf
#
28.09.202268.01 Кб2Таблица производных.pdf
#
28.09.20222.22 Mб9Терехина Фикс ВМ 2.PDF