
- •Принятые обозначения
- •Метод проекций
- •Евклидово пространство и его реконструкция
- •Центральное проецирование
- •Параллельное проецирование
- •Инвариантные свойства проецирования
- •Ортогональное проецирование. Точка, прямая, плоскость
- •Метод монжа. Октанты пространства
- •Проекции точки
- •Проекции прямых линий
- •Натуральная длина отрезка прямой и углы его наклона к плоскостям проекций
- •Проекции плоскости
- •Взаимное расположение простейших геометрических образов
- •Принадлежность прямой и точки плоскости
- •Параллельность прямой и плоскости, параллельность плоскостей
- •Перпендикулярность прямой и плоскости, перпендикулярность плоскостей
- •Пересечение прямой и плоскости, пересечение плоскостей
- •Преобразование чертежа
- •Способ перемены плоскостей проекций
- •Способ плоскопараллельного перемещения
- •Способ вращения
- •Примеры решения задач способами преобразования чертежа
- •Кривые линии
- •Локальные элементы кривой
- •Плоские кривые линии
- •Пространственные кривые линии и их проекции
- •Поверхности
- •Образование и задание поверхности на чертеже
- •Классификация поверхностей
- •Обзор некоторых поверхностей Торсовые поверхности
- •Поверхности с плоскостью параллелизма (поверхности Каталана)
- •Винтовые линейчатые поверхности (геликоиды)
- •Поверхности вращения
- •Линейчатые неразвертываемые поверхности с тремя направляющими
- •Поверхности параллельного переноса
- •Графические и топографические поверхности
- •Пересечение поверхности плоскостью и прямой, пересечение двух поверхностей
- •Пересечение поверхности плоскостью
- •Сечение поверхности плоскостью общего положения
- •Пересечение прямой линии с поверхностью
- •Пересечение поверхностей
- •Общие сведения
- •Способ плоскостей
- •Пересечение многогранников
- •Способ сфер
- •4. Примеры решения задач
- •Развертки поверхностей
- •Развертки прямых круговых цилиндра и конуса
- •Развертки линейчатых поверхностей
- •Развертки криволинейных поверхностей вращения
- •Аксонометрические проекции
- •Общие сведения
- •Прямоугольные проекции
- •Косоугольные проекции
Строятся развертки описанных цилиндров способом нормального сечения. Нормальное сечение каждой части (сечение, перпендикулярное образующим цилиндров) есть окружность 1 заданного диаметра d, которая разворачивается в прямую линию. На рис. 248 “развертка” нормального сечения изображается отрезком 1, 2, 3, ..., 8, 1 горизонтальной прямой. Перпендикулярно к этой линии через точки 1, 2, 3 и т.д. проводятся образующие цилиндров, размеры которых берут с фронтальной проекции. Для торцевых звеньев образующие I A5 I = I A2521 ... I B3 I = I B2321 ... Полученные точки A, B и C соединяют плавной кривой линией. Развертка звена симметрична относительно образующей A5. На практике обычно строится шаблон половины развертки торцевого звена (на рис. 248 заштрихованная часть). Повернув его вокруг образующей A5, очерчивается вторая половина развертки. На развертке среднего звена укладывается 4 таких шаблона.
Весь тор можно раскроить из листа железа без обрезков. Для этого развертки звеньев надо разместить на листе так, как показано на рис. 248. Из чертежа видно, что звенья разрезаются попеременно, то по образующей C1, то по образующей A5. Таким образом, при сборке тора швы на звеньях получаются прерывистыми.
В практике при раскрое даются припуски на швы в соответствии с типом соединения.
192
со
оо
Рис.
248
2 3 4 5 6 7 8 1

Аксонометрические
проекции (аксонометрия) служат для
наглядного изображения предметов.
Название “аксонометрия” образовано
из слов древнегреческого языка: “аксон”
- ось и “метрео” - измеряю, т.е. измерение
по осям.
Аксонометрическая
проекция предмета получается параллельным
проецированием его вместе с осями
прямоугольных координат, к которым
этот предмет отнесен, на одну плоскость
проекций, называемую аксонометрической
плоскостью проекций или картинной
плоскостью.
Аксонометрическая
проекция - это однокартинный чертеж,
на котором получается изображение
всех трех измерений предмета. Этим и
объясняется его наглядность.
На
рис. 249 схематично показано получение
аксонометрической проекции точки
А. Основные обозначения на рисунке
следующие:
П'
- аксонометрическая плоскость проекций;
x,
y,
z -
оси координат в пространстве;
А
- точка пространства;
А1
- проекция точки А на плоскость проекций
П1 (можно взять проекции точки А на
плоскость проекций П2
или П3);
5
- направление проецирования;
[O
X),
[O
y'), [O z)
-
аксонометрические оси, являющиеся
проекциями осей координат на плоскость
П'.
194
Рис.
249Аксонометрические проекции
Общие сведения

Аксонометрической
проекцией точки называется точка
пересечения проецирующего луча,
проведенного через заданную точку в
пространстве, параллельно направлению
проецирования, с аксонометрической
плоскостью проекций.
Таким
образом, чтобы получить аксонометрическую
проекцию точки А через нее проводят
проецирующий луч параллельно направлению
проецирования 5 до пересечения с
плоскостью проекций П' в точке А'.
Это
построение показывает, что при заданном
направлении проецирования каждой
точке А пространства на плоскости
проекций соответствует определенная
точка А'.
Но обратное утверждать нельзя. Проекции
А' на плоскости П' соответствует любая
точка проецирующего луча А'А.
Для
устранения этой неопределенности и
обеспечения взаимной однозначности
между точками пространства и точками
аксонометрической (картинной) плоскости
проекций, на плоскость П' проецируют
не только точку А, но и одну из ее
ортогональных проекций (обычно
горизонтальную проекцию А1). А'1 есть
вторичная проекция точки А.
Вторичной
проекцией точки называется аксонометрическая
проекция одной из ее ортогональных
проекций.
Этот
термин отражает тот факт, что точка А'1
получается в результате двух
последовательных проецирований точки
А (первое - точка А проецируется на
П1,
второе - А1
проецируется на П'). Аксонометрическая
проекция точки и ее вторичная проекция
однозначно определяют положение точки
в пространстве. Они находятся на одной
прямой, параллельной соответствующей
оси.
Коэффициенты
искажения
В
общем случае длина отрезков осей
координат в пространстве не равна длине
их проекций. Искажение отрезков осей
координат при их проецировании на
плоскость П' характеризуется коэффициентами
искажения.
Для
определения коэффициентов искажения
по аксонометрическим осям на осях x,
y, z
откладываются
отрезки длиной е, принимаемые за единицу
измерения по этим осям (см. рис. 249).
Величины е'х,
е'у,
e'z
являются
аксонометрическими проекциями этих
отрезков.
Коэффициентом
искажения называется отношение длины
аксонометрической проекции отрезка,
лежащего на координатной оси или
параллельного ей, к истинной длине
самого отрезка.
'а '
e A e
Kx=
—х,
Ky=
—
, Kz=
—z
-
коэффициенты искажения по осям x,
у
и
e e e
z,
соответственно.
195
В
инженерной практике при построении
аксонометрических проекций пользуются
не действительными коэффициентами
искажения, а приведенными, удобными
для построения. Обычно приведенные
коэффициенты искажения берут равными
единице, что значительно упрощает
построение. Изображение при этом
несколько увеличивается, однако это
не влияет на его наглядность.
При
помощи коэффициентов искажения можно
перейти от прямоугольных координат
к аксонометрическим и наоборот.
КЛАССИФИКАЦИЯ
АКСОНОМЕТРИЧЕСКИХ ПРОЕКЦИЙ
Аксонометрические
проекции классифицируют в основном по
двум признакам:
По
направлению проецирования.
В зависимости от направления проецирования все аксонометрические проекции делятся на две группы:
прямоугольные, если направление проецирования перпендикулярно аксонометрической плоскости проекций (5 А П');
косоугольные, если направление проецирования не перпендикулярно аксонометрической плоскости проекций (5 А П').
По коэффициентам искажения.
В зависимости от коэффициентов искажения все аксонометрические проекции делятся на три группы:
изометрия - коэффициенты искажения по всем трем осям равны между собой
(Кы= Ky = K);
диметрия - коэффициенты искажения по двум осям равны между собой, а третий им не равен
(Kx= Kz* Ky);
триметрия - коэффициенты искажения по всем трем осям не равны между собой
(Kx* Ky * Kz).
Между коэффициентами искажения и углом ф, образованным направлением проецирования с плоскостью П', существует следующая зависимость:
Kx2 + Ky2 + Kz2 = 2 + ctgg'j.
Сумма квадратов коэффициентов искажения по аксонометрическим осям равна двум плюс квадрату котангенса угла проецирования. Котангенс прямого угла равен нулю, следовательно, для прямоугольных аксонометрических проекций справедливо следующее уравнение:
Kx2 + Ky2 +Kz2 = 2.
196
З.ОСНОВНАЯ
ТЕОРЕМА АКСОНОМЕТРИИ
Всякое
изменение положения осей в пространстве
и направления проецирования влечет за
собой изменение положения аксонометрических
осей и коэффициентов искажения по осям.
Вопрос
в том, какие положения могут принимать
аксонометрические оси и какие величины
могут принимать коэффициенты искажения
по осям в зависимости от положения осей
проекций в пространстве и направления
проецирования, был разрешен в прошлом
веке геометрами Польке и Шварцем. Они
сформулировали основную теорему
аксонометрии: любой полный четырехугольник
на плоскости всегда является параллельной
проекцией некоторого масштабного
тетраэдра.
Если
на плоскости П1 (рис. 250 а) взять произвольно
четыре точки 0\,
А\, В\, С1
и соединить их попарно прямыми, то
получится фигура, называемая полным
четырехугольником (01А1В1С1).
Таким образом, полным является
четырехугольник с его диагоналями.
Если далее через эти точки провести
параллельные между собой прямые и взять
на каждой из них по произвольной точке
О, А, В и С так, чтобы все они не лежали
в одной плоскости, то в пространстве
образуется некоторый тетраэдр ОАВС
(рис. 250 б). Очевидно, тетраэдров в
пространстве, параллельной проекцией
которых может служить четырехугольник
0^А1В1С1,
может быть бесконечное множество. В их
числе содержится и тетраэдр с прямым
трехгранным углом при точке О и с
равными ребрами 0А'=
0В'= ОС =
е. Такой тетраэдр можно рассматривать
как масштабный, т.е. три равных и взаимно
перпендикулярных ребра этого
тетраэдра служат масштабами осей
координат в пространстве (рис. 250 в).
Отсюда, любые три прямые, проходящие
через одну из точек на плоскости и не
совпадающие между собой, могут быть
приняты за аксонометрические оси, т.е.
за проекции осей прямоугольных координат
(x,
y, z).
Рис.
250
197
огласно
основной теоре е аксоно етрии аксоно
ерические оси и коэффициенты искажения
по ним могут выбираться произвольно.
Задавая разные направления для любой
натуральной системы координат, можно
получить множество аксонометрических
проекций, отличающихся друг от друга,
как направлением аксонометрических
осей, так и величиной коэффициентов
искажения вдоль этих осей.
В
практике построения наглядных
аксонометрических изображений обычно
применяют некоторые определенные
комбинации направлений аксонометрических
осей и коэффициентов искажения, которые
дают реальное восприятие предмета
и удобны для построения.
СТАНДАРТНЫЕ
АКСОНОМЕТРИЧЕСКИЕ ПРОЕКЦИИ
Согласно
=ОСТ 2.317-69 рекомендуется применять пять
стандартных аксонометрических
проекций. Из прямоугольных аксонометрических
проекций применяют изометрию и диметрию,
из косоугольных - фронтальную
изометрию, горизонтальную изометрию
и фронтальную диметрию.
Название
отражает способ получения аксонометрических
проекций. Прямоугольная проекция
получена прямоугольным проецированием,
а слова «изометрия» или «диметрия»
говорят о расположении пространственных
координатных осей относительно картинной
плоскости.
Изометрическая
проекция.
В изометрии соблюдается равенство
коэффициентов искажения Kx
=
Ky
=
Kz.
Для
того чтобы получить искажения, равные
между собой, необходимо оси координат
в пространстве расположить относительно
картинной плоскости так, чтобы углы
наклона их к плоскости были одинаковые,
тогда проекции их изобразятся на П под
углом 120° друг к другу ( рис. 251).
2
2 2
В
прямоугольной аксонометрии Kx
+
Ky
+
Kz
=
2, Kx
=
Ky
=Kz,
откуда
3Kx2
=
2 и Kx
=
K=
Л
»
0,82.
Это
действительные коэффициенты искажения
по всем осям. =ОСТ рекомендует
изометрическую проекцию строить без
сокращения по осям координат (приведенные
коэффициенты искажения по всем осям
равны
единице),
что соответствует увеличению изображения
в —— = 1,22 раза.
0,82
Диметрическая
проекция.
Эта проекция получается прямоугольным
проецированием осей на одну плоскость
проекций П'. При этом оси x
и
z
располагаются
относительно картинной плоскости так,
чтобы углы накло-
198
Прямоугольные проекции

на
их были одинаковые, а ось у
так, чтобы коэффициент искажения по
ней был вдвое меньше.
Kx
=
Kz
;
Ky
=
1 Kx.
2
2
2 2
Подставляя
эти значения в формулу Kx
+Ky
+
Kz
=
2, будем иметь:
2Ky
+
Kx
2
V
У
=
2, откуда Kx
=
8;
Kx
=
Kz
»
0,94
; Ky
»
0,47.
V
9
Это
действительные коэффициенты искажения.
Так как в практике такие дробные числа
неудобны, то применяются приведенные
коэффициенты искажения: Kx
=
Kz
=
1; Ky
=
0,5.
При
этом изображение получается увеличенным
в = 1,06 раза.
При
указанном выше положении осей в
пространстве их проекции изображаются
так: ось z
-
вертикально, между осями X
и z
угол
97° 10', т.е. ось X
располагается под углом 7° 10' к
горизонтальной прямой, а ось у
под
углом 41°25' к ней (рис. 252).
Прямоугольные
аксонометрических проекций применяются
в машиностроительных чертежах.
Рис.
251
Рис.
252
У
косоугольных проекций обычно две оси
координат (х и z
или
x
и
у) располагаются параллельно картинной
плоскости, по этому они изображаются
без искажения. Для того чтобы получилось
изображение всех трех измерений
предмета, связанного с осями, направление
проецирования выбирается не под
прямым углом. При уголе j
равном
45°, по третьей оси искажения не возникает,
получается косоугольная изометрическая
проекция. Часто направление
проецирования выбирается такое, чтобы
коэффициент искажения по третьей
оси был равен 0,5, тогда получаются
косоугольные диметрические проекции.
199
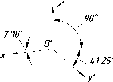
Косоугольные проекции
Фронтальная
изометрическая проекция.
Координатные оси x
и
z
располагаются
параллельно картинной плоскости. Таким
образом, фронтальная плоскость
проекций П2
будет параллельна картинной плоскости
П', поэтому такая аксонометрическая
проекция называется фронтальной. Все,
что расположено в плоскости П2
или в плоскостях ей параллельной, на
плоскости П' изобразится без искажения.
Коэффициенты искажения по всем осям
будут равны единице. Аксонометрические
оси (рис. 253) X
и z
располагаются
перпендикулярно друг другу, а ось у
- под углом 45° к горизонтальной
прямой. Допускается применять фронтальные
изометрические проекции с углом
наклона оси у,
равным 30 и 60°. Ось у
может быть обращена влево вниз, влево
вверх и т.д., что соответствует различному
направлению проецирования и
расположению плоскости проекций
относительно осей координат.
Косоугольная
фронтальная изометрическая проекция
применяется в сантехнических чертежах
при изображении аксонометрических
схем трубопроводов.
Горизонтальная
изометрическая проекция.
Координатные оси x
и
у
располагаются
параллельно картинной плоскости.
Горизонтальная плоскость проекций
Пь
определяемая этими осями, будет
параллельна картинной плоскости
П', поэтому аксонометрическая проекция
называется горизонтальной. Все, что
расположено в плоскости П1 или в
плоскостях ей параллельных, на
плоскости П' изображается без искажения.
Коэффициенты искажения по всем осям
принимаются равными единице.
Аксонометрические
оси X
и у
располагаются под прямым углом друг к
другу, а ось у
- под углом в 30° к горизонтальной прямой
(рис. 254). Допускается применять
горизонтальные изометрические проекции
с углом наклона оси у
= 45 и 60°, сохраняя угол между осями X,
у =
90°. В практике используется
горизонтальная косоугольная изометрия
с осями X
и у,
обращенными
вверх от точки O.
В этом случае предметы изображаются
при направлении проецирования снизу
вверх.
Этот
вид аксонометрии удобен при построении
наглядного изображения застройки
кварталов в инженерно-строительной
практике, при решении вопросов
пространственной композиции жилых
районов и архитектурных ансамблей.
Z
Z
\К30°(45°,
60°)
90°У^
у'
Рис.
253
Рис.
254
200
Фронтальная
диметрическая проекция.
Координатные оси x
и
z,
а
следовательно,
и плоскость П2
располагаются параллельно
картинной
плоскости П'. Коэффициенты
искажения по
осям
X
и z
равны
единице, а
по
оси
у
коэффициент принимается равным 0,5.
Аксонометрические
оси X
и z
располагаются
под прямым углом, а
ось
у
- под углом 45° к горизонтальной
прямой
(рис. 255). Допускается применять
фронталь-
ные диметрические проекции
с углом наклона
оси у
равным 30 и 60°.
Этот
вид аксонометрии применяется
в
машиностроительных чертежах при
изображе-
нии деталей, имеющих большое
количество ок-
ружностей, расположенных
фронтально (дета-
ли типа валика).
ПОСТРОЕНИЕ
АКСОНОМЕТРИЧЕСКОЙ ПРОЕКЦИИ ОКРУЖНОСТИ
ПО ВОСЬМИ ТОЧКАМ
При
параллельном проецировании окружности
на какую-либо плоскость получаем ее
изображение, в общем случае, в виде
эллипса. Отдельные точки окружности
строятся как точки пересечения двух
прямых, удобных для построения. Обычно,
в качестве таких прямых берут стороны
описанного квадрата и его диагонали.
В аксонометрии квадрат в общем случае
изображается в виде параллелограмма,
т.к. при параллельном проецировании
параллельность прямых сохраняется. На
рис. 256 показано построение
аксонометрической проекции окружности
в прямоугольной изометрии, а на рис.
257 - в прямоугольной диметрии.
Рис.
256
201
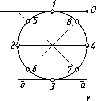

Четыре
точки касания сторон квадрата с
окружностью 1, 2, 3, 4 в аксонометрии
будут находиться на середине каждой
стороны параллелограмма. Еще четыре
точки 5, 6, 7, 8 находятся на пересечении
диагоналей параллелограмма со
вспомогательными прямыми. Они проведенны
параллельно соответствующим
аксонометрическим осям на расстояниях,
равных отрезку z.
Соединив
полученные восемь точек плавной кривой,
получают эллипс.
В
прямоугольных изометрии и диметрии
большие оси эллипсов перпендикулярны
отсутствующим в плоскости эллипса
осям, а малые оси по направлению совпадают
с ними.
Например,
эллипс, построенный в плоскости X
о' у,
имеет большую ось, перпендикулярную
оси z,
а малую - совпадающую с направлением
оси z
.
Косоугольные
аксонометрические проекции окружности
строятся аналогично.
При
построении диметрической проекции
окружности надо учитывать коэффициент
искажения по оси у,
который равен 0,5.
Рис.
257
202

6.
ПОСЛЕДОВАТЕЛЬНОСТЬ
ПОСТРОЕНИЯ АКСОНОМЕТРИЧЕСКИХ ПРОЕКЦИЙ
Переход
от ортогональных проекций предмета к
аксонометрическим проекциям рекомендуется
осуществлять в такой последовательности:
на
ортогональном чертеже обозначают оси
прямоугольной системы координат,
к которой и относят данный предмет.
Оси ориентируют так, чтобы они допускали
удобное измерение координат точек
предмета. У поверхностей вращения эти
оси целесообразно совмещать с осями
симметрии, а у гранных поверхностей
- с ребрами;
строят аксонометрические оси с таким расчетом, чтобы была обеспечена наилучшая наглядность изображения и видимость отдельных элементов предмета;
по одной из ортогональных проекций предмета чертят вторичную проекцию. Вычерчивать рекомендуется ту вторичную проекцию предмета, которая проще других. Таким образом, используют два измерения предмета;
создают аксонометрическое изображение, откладывая третье измерение предмета, от соответствующих вторичных проекций.
На рис. 258 показано построение точки Л в прямоугольной изометрии по заданным ортогональным проекциям. Построение выполнено в следующей последовательности:
относят точку Л к координатным осям x, у, z,
проводят аксонометрические оси x, y, z' под углом 120° друг к другу;
строят вторичную проекцию точки Л по ее горизонтальной проекции. Для этого измеряют координаты x и у на координатных осях и откладывают их на аксонометрических осях x и y . Через полученные точки проводят прямые, параллельные соответствующим аксонометрическим осям x и у. На пересечении этих линий находится точка Л' i - вторичная проекция точки Л,
Z
N
А'о
А
хХ
О
х
N о'
<?А
X

У
Рис. 258
203
строят
аксонометрическую проекцию точки А.
Для этого через вторичную проекцию А\
проводят прямую, параллельную
аксонометрической оси z
и
на этой прямой откладывают отрезок,
равный координате z.
Получается
точка А'
-
аксонометрическая проекция точки А.
Аксонометрическая
и вторичная проекции точки вполне
определяют ее положение в пространстве.
Построение
конуса в прямоугольной изометрии
показано на рис. 259. Построение начато
со вторичной проекции окружности,
которая в аксонометрии проецируется
в эллипс. Построение эллипса выполняют
по 8 точкам. От центра эллипса
откладывают высоту конуса и получают
точку S'
- вершину
конуса. Из точки S'
касательно к эллипсу проводят образующие
и получают аксонометрическую проекцию
прямого кругового конуса.
Z
X
X
У
Рис.
259
204
БИБЛИОГРАФИЧЕСКИЙ
СПИСОК
Гордон
В.О. Курс начертательной геометрии:
Учеб. пособие для втузов. - М.: Высшая
школа, 2000. - 271 с.
Начертательная геометрия: Учеб. для втузов / Н.Н. Крылов, Г.С. Иконникова, В.Л. Николаев, В.Е. Васильев. - М.: Высшая школа, 2000. - 224 с.
Чекмарев А. А. Начертательная геометрия и черчение: Учеб. для втузов. - М.: Владос, 1999. - 244 с.
Иванов Г.С. Начертательная геометрия: Учеб. для втузов. - М.: Машиностроение, 1999. - 223 с.
Локтев О.В. Краткий курс начертательной геометрии: Учеб. пособие для втузов. - М.: Высшая школа, 1999. - 136 с.
Начертательная геометрия: Конспект лекций / Е.П. Александрова, Т.В. Грошева, Е.С. Дударь, С.В. Томилова; Под ред. Лалетина В. А.; Перм. гос. техн. ун-т. - Пермь, 1995 - 252 с.
Лалетин
В.А., Александрова Е.П., Грошева Т.В.,
Дударь Е.С., Корнилкова Е.В.
НАЧЕРТАТЕЛЬНАЯ
ГЕОМЕТРИЯ
Учебное
пособие
Редактор Н.В.
Бабинова
Техн.
редактор Н.А. Щепина
Компьютерный
набор текста О.В. Шибановой,
О.Л.
Бабушкиной
Лицензия
№ 020370
Подписано
в печать 08.10.2002. Формат 60 х 90 V8.
Усл.
печ. л. 25,75. Тираж 500 экз. Заказ 114.
Редакционно
-издательский отдел и ротапринт Пермского
государственного технического
университета 614600. Пермь, Комсомольский
пр., 29а.
