- •Принятые обозначения
- •Метод проекций
- •Евклидово пространство и его реконструкция
- •Центральное проецирование
- •Параллельное проецирование
- •Инвариантные свойства проецирования
- •Ортогональное проецирование. Точка, прямая, плоскость
- •Метод монжа. Октанты пространства
- •Проекции точки
- •Проекции прямых линий
- •Натуральная длина отрезка прямой и углы его наклона к плоскостям проекций
- •Проекции плоскости
- •Взаимное расположение простейших геометрических образов
- •Принадлежность прямой и точки плоскости
- •Параллельность прямой и плоскости, параллельность плоскостей
- •Перпендикулярность прямой и плоскости, перпендикулярность плоскостей
- •Пересечение прямой и плоскости, пересечение плоскостей
- •Преобразование чертежа
- •Способ перемены плоскостей проекций
- •Способ плоскопараллельного перемещения
- •Способ вращения
- •Примеры решения задач способами преобразования чертежа
- •Кривые линии
- •Локальные элементы кривой
- •Плоские кривые линии
- •Пространственные кривые линии и их проекции
- •Поверхности
- •Образование и задание поверхности на чертеже
- •Классификация поверхностей
- •Обзор некоторых поверхностей Торсовые поверхности
- •Поверхности с плоскостью параллелизма (поверхности Каталана)
- •Винтовые линейчатые поверхности (геликоиды)
- •Поверхности вращения
- •Линейчатые неразвертываемые поверхности с тремя направляющими
- •Поверхности параллельного переноса
- •Графические и топографические поверхности
- •Пересечение поверхности плоскостью и прямой, пересечение двух поверхностей
- •Пересечение поверхности плоскостью
- •Сечение поверхности плоскостью общего положения
- •Пересечение прямой линии с поверхностью
- •Пересечение поверхностей
- •Общие сведения
- •Способ плоскостей
- •Пересечение многогранников
- •Способ сфер
- •4. Примеры решения задач
- •Развертки поверхностей
- •Развертки прямых круговых цилиндра и конуса
- •Развертки линейчатых поверхностей
- •Развертки криволинейных поверхностей вращения
- •Аксонометрические проекции
- •Общие сведения
- •Прямоугольные проекции
- •Косоугольные проекции
Министерство
образования Российской Федерации
Пермский государственный технический
университет Кафедра инженерной графики
В.
А. Лалетин, Е.П. Александрова, Т.В. Грошева,
Е.С. Дударь, Е.В. Корнилкова
НАЧЕРТАТЕЛЬНАЯ
ГЕОМЕТРИЯ
Утверждено
редакционно-издательским советом
университета в качестве учебного
пособия
ПЕРМЬ
2002
УДК
514.18
(075.8) Л
46
Рецензента:
Доктор
технических наук, профессор кафедры
механики и инженерной графики ПВВКИУ
РВ B.C.
Елтышев
Кандидат
технических наук, профессор кафедры
Пермского государственного
технического университета Б.П.
Свешников
Лалетин
В.А. и
др.
Л
46. Начертательная геометрия: Учебное
пособие /В .А. Лалетин, Е.П. Александрова,
Т.В. Грошева, Е.С. Дударь, Е.В. Корнилкова;
Перм. гос. техн. ун-т. - Пермь, 2002. - 205 с.
ISBN
5-88151-039-9
Изложены
основные способы изображений и
исследований геометрических образов,
рассматриваются позиционные и метрические
задачи, имеющие практическое значение.
Пособие
составлено с учетом современных
требований к геометрической науке,
отличается более полной проработкой
основных теоретических положений
курса и обобщением приемов решения
задач, что способствует более
глубокому изучению курса.
Предназначено
для студентов втузов всех специальностей,
изучающих курс начертательной
геометрии.
Авторы
приносят благодарность С.В. Томиловой
за предоставленные материалы.
ISBN
5-88151-039-9
УДК
514.18 (075.8)
©
Пермский государственный технический
университет, 2002
ОГЛАВЛЕНИЕ
Введение
5
Метод
проекций 9
Евклидово
пространство и его реконструкция 9
Центральное
проецирование 11
Параллельное
проецирование 11
Инвариантные
свойства проецирования 13
Обратимость
проекционных чертежей 18
Ортогональное
проецирование. Точка, прямая, плоскость
20
Метод
Монжа. Октанты пространства 20
Проекции
точки 22
Проекции
прямых линий 27
Проекции
плоскости 35
Взаимное
расположение простейших
геометрических образов . . . . 41
Принадлежность
прямой и точки плоскости 41
Параллельность
прямой и плоскости, параллельность
плоскостей 46
Перпендикулярность
прямой и плоскости, перпендикулярность
плоскостей . 48
Пересечение
прямой и плоскости, пересечение
плоскостей 51
Примеры
решения задач 60
Преобразование
чертежа 70
Способ
перемены плоскостей проекций 70
Способ
плоскопараллельного перемещения 76
Способ
вращения 79
Примеры
решения задач способами преобразования
чертежа 86
Кривые
линии 91
Локальные
элементы кривой 92
Свойства
проекций кривой линии 93
Плоские
кривые линии 94
Плоские
кривые линии второго порядка и их
проекции 97
Пространственные
кривые линии и их проекции 104
Поверхности
106
Образование
и задание поверхности на чертеже 106
Классификация
поверхностей 108
Обзор
некоторых поверхностей 108
Пересечение
поверхности плоскостью и прямой,
пересечение 134
двух
поверхностей
Пересечение
поверхности плоскостью 134
Пересечение
прямой линии с поверхностью 152
Пересечение
поверхностей 156
Примеры
решения задач 168
Развертки
поверхностей 180
Развертки
прямых круговых цилиндра и конуса 180
Развертки
линейчатых поверхностей 181
Развертки
криволинейных поверхностей вращения
186
Примеры
построения разверток некоторых
поверхностей 190
Аксонометрические
проекции 194
Общие
сведения 194
Классификация аксонометрических проекций 196
Основная теорема аксонометрии 197
Стандартные аксонометрические проекции 198
Построение аксонометрических проекций окружности по восьми точкам . . . 201
Последовательность построения аксонометрических проекций 203
Библиографический список 205
ВВЕДЕНИЕ
Предметом
начертательной геометрии является
изложение и обоснование способов
построения изображения пространственных
форм на плоскости и способов решения
геометрических задач по заданным
изображениям этих форм.
Основными
требованиями, предъявляемыми к методам
изображения на плоскость, являются
наглядность, точность изображения и
его обратимость, геометрическая
равноценность оригиналу. Изображения,
построенные по правилам начертательной
геометрии, дают возможность решать с
помощью плоских изображений
общегеометрические и прикладные
задачи.
Наряду
с задачей изображения пространственных
форм в плоскости чертежа начертательная
геометрия дает возможность решать с
помощью плоских изображений различные
задачи в пространстве. Все задачи
начертательной геометрии условно
делятся на три основных класса:
позиционные, метрические и комплексные.
Позиционными
называются задачи на определение общих
элементов геометрических фигур. Вопросы
принадлежности точки или линии
какому-либо геометрическому образу,
задачи на пересечение и параллельность
геометрических фигур относятся к классу
позиционных. В позиционных задачах
выясняются вопросы, связанные с взаимным
расположением геометрических
образов, а вопросы измерений не
затрагиваются.
Метрическими
называются задачи, в которых требуется
определить геометрические величины:
расстояния, углы, площади, объемы и т.д.
К этому классу относятся задачи на
определение длины отрезка прямой и
углов его наклона к плоскостям проекции,
расстояния между различными геометрическими
образами и др.
Комплексные
задачи включают в себя как вопросы
взаимного расположения геометрических
образов, так и вопросы их измерения.
Начертательная
геометрия по своему содержанию и методам
занимает особое положение среди
других наук. Обогащая точные науки
наглядностью и простотой решения
многих проблем, начертательная геометрия
находит применение в механике,
кристаллографии, оптике, то есть всюду,
где возникает необходимость в
пространственных построениях. Все
задачи, изучаемые в аналитической
геометрии, могут быть решены графическими
методами начертательной геометрии.
Как
и другие точные науки, начертательная
геометрия развивает логическое и
абстрактное мышление, пространственное
воображение.
5
П',
По - плоскость проекции и поле проекций
(прописная буква греческого алфавита
[пи]);
П1
- горизонтальная плоскость проекций;
П2
- фронтальная плоскость проекций;
П3
- профильная плоскость проекций;
П4,
П5,
П6
- новые плоскости проекций, отличные
от указанных выше;
x,
y, z
-
оси проекций (строчные буквы латинского
алфавита);
A,
B, C,
...
, 1, 2, 3, ... - точки пространства (прописные
буквы латинского алфавита и арабские
цифры) ;
a,
b m,
n,
...-
прямые и кривые линии пространства
(строчные
буквы
латинского алфавита, кроме x,
y, z, h,
f p);
h
- горизонталь;
f-
фронталь;
p
- профильная
прямая уровня;
0
[тэта], А [дельта], Л [ламбда], Р [ро], Т
[тау],Е [сигма], Q
[омега]
- плоскости и поверхности (прописные
буквы греческого алфавита, кроме П, Г,
Ф, ^);
Г
[гамма] - горизонтальная плоскость
уровня;
Ф
[фи] - фронтальная плоскость уровня;
¥
[пси] - профильная плоскость уровня;
а
- угол наклона прямой (плоскости) к
горизонтальной плоскости проекций П1;
Р
- угол наклона прямой (плоскости) к
фронтальной плоскости проекций П2;
у
- угол наклона прямой (плоскости) к
профильной плоскости проекций П3.
6Принятые обозначения
Проекции
геометрических образов обозначают
теми же буквами, какими обозначены
их оригиналы, и добавляют подстрочный
индекс, соответствующий индексу
плоскости проекций:
A\,
A2,
A3
—
горизонтальная, фронтальная и профильная
проекции точки A;
a\,
а2,
а3
—
горизонтальная, фронтальная и профильная
проекции линии а;
Еь
S2,
S3
—
горизонтальный, фронтальный и профильный
следы плоскости S.
Символы:
е
, с — принадлежность;
— параллельность;
@ — пересечение;
— скрещивание;
А —
перпендикулярность;
° — совпадение;
= — результат
геометрических операций;
* — касание;
],
□ — прямой угол;
^ — следует;
: — соответствует;
I
|
— расстояние;
U
—
соединение.
7
Наклонная
черта (/), перечеркивающая тот или иной
символ, означает отрицание данного
действия:
а
□ b
—
прямая а
не параллельна прямой b.
ри
ер использования си волов:
А
е S —
точка A
принадлежит
плоскости S;
l
□
A — прямая l проходит через точку A;
A1
°
B1 —
горизонтальные проекции точек A
и
B
совпадают;
S
(а
□ b) —
плоскость задана параллельными прямыми
а
и b;
Q
@
0 = A —
плоскости Q
и
0 пересекаются по прямой а;
а
А b —
прямая а
перпендикулярна прямой b;
A1
:
A2 —
данной проекции A1
соответствует
проекция A2 или
по
данной
проекции A1
строится
проекция A2
при
определенном условии;
IabI
—
расстояние между точками A
и
B;
I
AS I
— расстояние от точки A
до
плоскости S;
I
а
b
I
— расстояние между прямыми A
и
B.
Сокращения:
н.ч.
— начертательная геометрия; г.о. —
геометрические образы; пл. пр. — плоскость
проекций; г.м.т. — геометрическое место
точек; н.в. — натуральная величина; т.
— точка.
8
В
основе начертательной геометрии лежит
метод проекций (проецирования). Слово
«проекция» (projecere)
-
латинского происхождения. Оно означает
«бросить вперед, вдаль». Таким образом,
под проекцией предмета на плоскость
подразумевают его изображение,
«отброшенное» на эту плоскость с помощью
воображаемых проецирующих лучей,
подобно тому, как предмет, освещенный
солнцем, отбрасывает тень на землю
(рис. 1).
Рис.
1
При
проецировании решается прямая задача
начертательной геометрии, т.е.
трехмерные объекты (предметы, оригиналы)
изображаются на плоскости, строится
чертеж.
Геометрическое
пространство, в котором рассматриваются
трехмерные объекты и их элементарные
составляющие - геометрические образы
(г.о.) (точка, прямая, плоскость,
поверхность), до некоторого времени
именовалось Евклидовым пространством.
Для него справедливы описанные геометром
древности Евклидом пять аксиом:
сочетания, порядка, движения,
непрерывности, параллельности.
Однако
принятие аксиомы Евклида о параллельности
приводит к трудностям, связанным с
неоднородностью евклидова пространства
и погруженных в него г.о., когда речь
заходит о проецировании.
Действительно,
пусть даны две прямые а
и b,
принадлежащие
плоскости (рис. 2).
В
плоскости S
через
произвольную точку S
проводится
прямая 1, которая пересекает прямую
а
в точке А и прямую b
в
точке В. Точка А на прямой а
однозначно соответствует точке В на
прямой b.
Аналогично
рассуждают о взаимном соответствии
точек А' ... Ап
прямой а,
точкам В' ... Вп
прямой b.
9Метод проекций
Евклидово пространство и его реконструкция

Если
проводится l
к
параллельно b
и
l
1
параллельно а,
то однородность прямых а
и b
нарушается,
так как на прямой а
нет точки А 1
и на прямой b
нет
точки В k,
которые
соответствовали бы точкам В
1
и А k.
Таким
образом, прямые а
и b
вследствие
свойств параллельности являются
неоднородными, следовательно, будет
неоднородным и плоское поле (евклидова
плоскость), определяемое этими прямыми.
Русский
математик Н.И. Лобачевский (1792-1856)
предложил считать пространство
(плоскость) однородным, подвергнув
сомнению существование аксиомы о
параллельности. Ученый дополнил
плоскость S
бесконечно
удаленными (несобственными) точками А
1
и В k,
в
которых параллельные прямые l
1
и а,
l
k
и
b
пересекаются.
Собственными элементами принято
называть прямые и плоскости, расположенные
в ограниченном (конечном) пространстве.
Рис.
2
Добиться
однородности трехмерного евклидова
пространства можно путем добавления
к нему несобственных (бесконечно
удаленных) прямых.
Евклидовы
плоскость и пространство, дополненные
бесконечно удаленными точками,
прямыми и плоскостями, называются
проективными.
Для
проективной плоскости справедливы
утверждения:
через
любые две различные точки проходит
прямая, и только одна;
любые
две прямые имеют общую точку, и только
одну.
В
проективном пространстве:
любые
две прямые, лежащие в одной плоскости,
всегда пересекаются;
любые
две плоскости пересекаются по прямой;
всякая
прямая, не лежащая в плоскости, всегда
пересекает плоскость.
Создав
пространство, в котором без всяких
исключений может осуществляться
операция проецирования, рассмотрим
способы получения центральных и
параллельных проекций.
10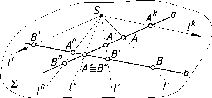
Центральное
проецирование представляет собой один
из общих случаев проецирования г.о.
на плоскость. Аппарат центрального
проецирования определяют плоскость
проекций П' и вне ее точка S
-
центр проекций. Проецирование называется
центральным, если все проецирующие
лучи проходят через одну и ту же точку
- центр проецирования.
Чтобы
спроецировать любую точку пространства
на плоскость проекций П', через центр
проекций и точку проводится проецирующий
луч SA
до
пересечения с плоскостью проекций в
точке А' (рис. 3). Так как через две точки
можно провести только одну прямую,
которая с плоскостью проекций П'
пересекается в единственной точке, то
можно заключить, что любая точка
пространства имеет одну вполне
определенную проекцию.
Таким
образом, центральной проекцией какой-либо
точки пространства называется точка
пересечения проецирующего луча,
проходящего через центр проекций и
данную точку, с плоскостью проекций.
5
Рис.
3 Рис. 4
Центральное
проецирование называют также коническим,
так как проецирующие лучи, проходящие
через точки кривой линии к
(рис. 4), представляют собой коническую
поверхность с вершиной в центре S.
Параллельное
проецирование является частным случаем
центрального проецирования, когда
центр проекций находится в бесконечно
удаленной точке S4.
Аппарат параллельного проецирования
определяют плоскость проекций П' и
вектор 5,
который называют направлением
проецирования (рис. 5). Проецирование
называется параллельным, если все
проецирующие лучи параллельны между
собой.
Чтобы
спроецировать точку А
пространства на плоскость П', через
точку А проводится проецирующая прямая
1, параллельная направлению проецирования
5
, до пересечения с плоскостью проекций
в точке А'
11Центральное проецирование
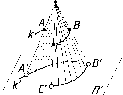

Параллельное проецирование
(см.
рис. 5). Любая точка пространства имеет
одну вполне определенную проекцию, так
как через точку можно провести параллельно
вектору 5
один
проецирующий луч, который пересекает
плоскость П' в единственной точке Л'.
Параллельной
проекцией какой-либо точки пространства
называется точка пересечения проецирующего
луча, параллельного направлению
проецирования, с плоскостью проекций.
Множество
проецирующих лучей, проходящих
через точки кривой линии к,
образуют цилиндрическую поверхность,
поэтому параллельное проецирование
именуют цилиндрическим (рис. 6).
зависи
ости от угла наклона проециру его луча
к плоскости проекций параллельные
проекции делятся на косоугольные, если
угол отличен от прямого (рис. 7), и
прямоугольные, если проецирующий луч
перпендикулярен плоскости проекции
(рис. 8).
Прямоугольные
проекции называют также ортогональными
(от греческого слова «ортос» - прямой).
В
Рис.
5
Рис.
6
Рис.
7
Рис.
8
12
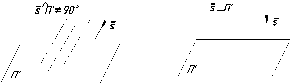
Геометрические
образы проецируются на плоскость
проекций в общем случае с искажением.
При этом характер искажения проекции
по сравнению с оригиналом зависит от
аппарата проецирования и положения
проецируемого предмета относительно
плоскости проекций. В частности, при
параллельном проецировании нарушаются
метрические характеристики.
Наряду
с этим, между оригиналом и его проекцией
существует определенная связь,
заключающаяся в том, что некоторые
свойства оригинала сохраняются и на
его проекции.
Такие
свойства принято называть проективными
или инвариантными (независимыми) для
данного способа проецирования.
Общие
свойства центрального и параллельного
проецирования
Свойство
1.
Проекция точки есть точка.
Это
свойство следует из самого способа
построения проекции точки.
Свойство
2.
Проекция кривой линии есть кривая
линия.
Действительно,
проецирующие коническая (см. рис. 4) или
цилиндрическая (см. рис. 6)
поверхности, проходящие через данную
кривую, пересекаются с плоскостью
проекций по кривой линии.
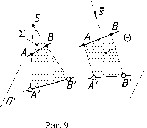
Свойство
3.
Проекция прямой есть прямая (рис. 9).
Проецирующие
лучи образуют проецирующие плоскости
S
(SA @
SB)
и
0 (::'
//
<<'). Две плоскости пересекаются по
прямой линии: S
@
П' = :'<'и 0 @ П' = :'<'.
Следовательно, :'<'-
прямая.
Для
построения проекции прямой достаточно
построить проекции двух ее точек и
соединить их.
13Инвариантные свойства проецирования
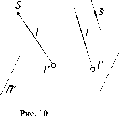
Исключение
представляет собой прямая 1, совпадающая
с проецирующим лучом. Такая прямая
проецируется (вырождается) в точку
(рис.10). Точка 1
- вырожденная проекция прямой 1.
Свойство
4
(это свойство известно как собирательное
свойство проекций проецируемых
г.о.).
Проекции
любых точек А,
В, С,
..., принадлежащих проецирующей прямой,
совпадают с ее вырожденной проекцией
(рис. 11),
а также проекции любых точек А, В,
..., прямых или кривых линий, принадлежащих
проецирующей плоскости, совпадают
с вырожденной проекцией этой плоскости
(рис. 12).
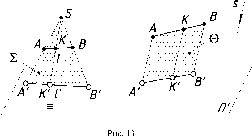
Свойство
5.
Если точка принадлежит прямой, то
проекция точки принадлежит проекции
прямой (рис. 13).
Проецирующий
луч 1, проходящий через точку K,
лежит
в проецирующей плоскости и пересекает
плоскость П' в точке К,
находящейся на линии пересечения двух
плоскостей АВВ'А' и П'.
Из
свойства 5 вытекают два следующих (6,
7):
14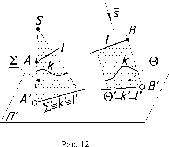
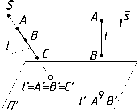
Свойство
6.
Точка пересечения линий проецируется
в точку пересечения проекций этих
линий (рис. 14).
Свойство
7.
Прямая, касательная к кривой линии,
проецируется в касательную к проекции
данной кривой (рис. 15).
Свойства
параллельного (в том числе ортогонального)
проецирования
Свойство
8.
Проекции параллельных прямых параллельны
(рис. 16). Плоскости S
и
0 параллельны. Линии пересечения их
третьей плоскостью П' также параллельны,
т.е. а'
|| b'.
Свойство
9.
Отношение отрезков, принадлежащих
параллельным прямым или одной прямой,
равно отношению проекций этих отрезков.
Доказательство
для двух параллельных прямых
(см. рис. 16) Проводятся [AE]
||
[Л'В]
и [CF]
||
[СП].
Из подобия □АВЕ
и □CDF
следует:
М
= И, а так как |АЕ| = | Л'В\
и |CF|
=
| СП\,
то,
[AE
]
[CF
] [А
В] [CD]
что
и требовалось доказать.
15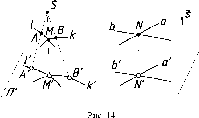
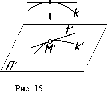
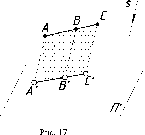
Доказательство
для одной прямой
(рис. 17).
Известно,
что длины отрезков двух прямых АС
и А'С',
заключенных между параллельными прямыми
АА' || ВВ'
|| СС',
пропорциональны. Значит,
[Щ
= [BC
]
\АЕ] [ВО1]
'
Свойство
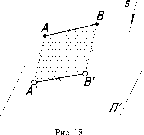
10.
Любой отрезок прямой, параллельной
плоскости проекций, проецируется
на эту плоскость без искажения (рис.
18).
АВВ'А'
- параллелограмм, так как (АА')
|| (ВВ')
и |АА'| = 1ВВ_,
то и (АВ)
|| (А'В') и |AB|
=
|A'B'|.
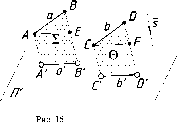
Свойство
11.
При параллельном переносе плоскости
проекций величина проекций не
меняется (рис. 19).
А'В'В"А"
- параллелограмм, так как [A'A"]
||
[B'B"]
и
[A'B]
||
[A"B'],
то
| A'B'|
=
| A"B"|.
Свойства
ортогонального проецирования
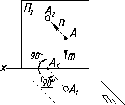
Свойство
12.
Отрезок прямой в общем случае равен
гипотенузе прямоугольного треугольника,
у которого один катет равен его проекции
на данную плоскость проекций, а другой
- разности расстояний концов отрезка
от этой плоскости (рис. 20).
Из
чертежа модели (см. рис. 20) видно, что
длину отрезка прямой АВ
можно
определить из прямоугольного треугольника
АВА0,
в котором катет |А0В|
= |A'B'|
(проекции
отрезков АВ
на плоскость П'), а катет АА0
равен DZ
-
разности расстояний точек А
и В
от плоскости П'. Угол ф в том же
треугольнике определяет угол наклона
отрезка прямой АВ
к плоскости проекций.
16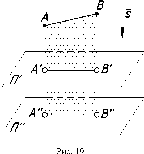
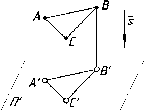
Свойство
13.
Любая плоская фигура, параллельная
плоскости проекций, проецируется
на эту плоскость без искажения (рис.
21).
Если
треугольник ABC
параллелен
плоскости проекций П', то на основании
свойства 10
проекции сторон равны самим сторонам
треугольника, т.е. DA'B'C'
@
IHIABC.
Рис.
20 Рис. 21
Свойство
14.
Проекция любого г.о. не может быть больше
самой фигуры. Это свойство вытекает из
свойств 10, 12, 13.
Свойство
15
(известно как теорема о проецировании
прямого угла).
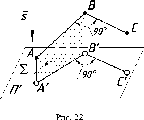
Если
одна сторона прямого угла параллельна
плоскости проекций, а другая ей не
перпендикулярна, то на эту плоскость
проекций прямой угол проецируется без
искажения (рис. 22).
Дано:
Z
ABC =
90°, BC
||
П', AB
□
I'. Доказать, что Z
A'B'C' =
90°.
Доказательство:
прямая AB
заключается
в проецирующую плоскость S
(ABB'A').
Так как BC
1AB,
то
BC
1
S.
Но
BC
||
П', значит BC
||
B'C'.
А
так как BC
1
S,
то
и B'C'1
S, поэтому
B'C'
перпендикулярна
любой прямой плоскости S,
в
том числе и A'B'.
Следовательно,
угол A'B'C'
равен
90°.
17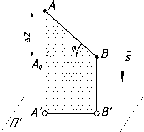
ОБРАТИМОСТЬ
ПРОЕКЦИОНЫХ ЧЕРТЕЖЕЙ
Выше
приводились рисунки - модели
однопроекционных чертежей,
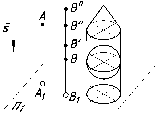
По
одной проекции окружности нельзя
определить, какой г.о. спроецирован
на П1.
Это может быть сфера, конус, цилиндр и
некоторые другие поверхности (см. рис.
23). Одна проекция не определяет форму
и положение г.о. в пространстве.
Необходима дополнительная информация,
чтобы чертеж был обратимым, т.е. однозначно
определял форму и размер предмета
по чертежу.
В
зависимости от способа дополнения
однопроекционного чертежа существуют
следующие методы:
ортогональные
проекции (метод Монжа);
проекции
с числовыми отметками;
аксонометрические
проекции;
перспективные
проекции.
В
методе Монжа дополнением однопроекционного
чертежа является проекция на вторую
плоскость (рис. 24, 25). Более подробно
этот метод изложен в разделе II.
где
проецирование в полнялось на
одну
плоскость проекций. Был сде-
лан
важный вывод о том, что точка А
пространства
имеет одну вполне оп-
ределенную
проекцию А1
(рис. 23) -
прямая задача н.г.
Рис.
23
Обратная
задача - определение
положения точки
по заданной проек-
ции - однозначно
не решается, так
как не известно, на
каком расстоянии
находится искомая
точка от плоско-
сти проекций. Проекции
В1
может
соответствовать любая точка
В,
В', ...,
Вп
пространства (см. рис. 23).
X
18
Рис.
24
Рис.
25
В
проекциях с числовыми отметками одну
ортогональнуо проек-
цию точки
дополняет числовая отметка, указывающая
расстояние от
точки
до плоскости проекций (рис.
26).
На
чертеже обязательно
приводится
линейный масштаб,
который вместе
с числовой от-
меткой позволяет
сделать чертеж
обратимым.
Проекции
с числовыми отметками применяются
в инженерно-строительном деле или
при изображении объектов, у которых
высота невелика по сравнению с длиной
и шириной.
Обратимость
аксонометрических проекций (рис. 27)
и перспективных проекций (рис. 28)
достигается благодаря так называемым
вторичным проекциям (А\)
точек пространства. Более полные
сведения об аксонометрических
проекциях приведены в разделе IX.
-10
12
По
i
i
Рис.
26
|
. гг |
A'i с |
3 |
Рис.
27
Рис.
28
19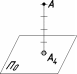
Из
всех методов проецирования ортогональное
нашло наиболее широкое применение
в инженерной практике в силу ряда своих
преимуществ. Наиболее важным из них
является возможность при определенных
условиях сохранить на проекциях
форму и размеры проецируемой фигуры.
При этом при получении ортогонального
чертежа, обладающего полной обратимостью,
необходимо иметь, как было отмечено
ранее, по крайней мере, две связанные
между собой ортогональные проекции
оригинала.
Наиболее
удобной для фиксирования положения
геометрического образа в пространстве
и выявления его формы по ортогональным
проекциям является система из трех
взаимно перпендикулярных плоскостей
проекций. Такой плоскостной макет
представлен на рис. 29. При этом различают:
П1
- горизонтальная плоскость проекций;
П2
- фронтальная плоскость проекций;
П3
- профильная плоскость проекций.
Плоскости
проекций пересекаются по трем взаимно
перпендикулярным прямым, которые
называются осями проекций (x,
у,
z).
Оси
проекций пересекаются в общей точке
трех плоскостей проекций - точке 0.
В
большинстве европейских стран принята
система расположения плоскостей
проекций, при которой положительными
направлениями осей считают: для оси x
-
влево от точки 0,
для оси у
- в сторону зрителя (вперед) от
плоскости П2,
для z
-
вверх от плоскости П1;
противоположные направления осей
считают отрицательными.
20Ортогональное проецирование. Точка, прямая, плоскость
Метод монжа. Октанты пространства
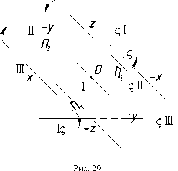
Плоскости
проекций делят пространство на восемь
частей - октантов. Октанты условно
принято нумеровать, как показано на
рис. 29.
Принято,
что наблюдатель всегда находится в
первом октанте. Плоскости проекций
считаются непрозрачными, поэтому видимы
только точки (геометрические фигуры),
расположенные в I октанте, а также на
полуплоскостях Пь П2,
П3.
Пользоваться
пространственным макетом для изображения
проекций оригинала неудобно ввиду его
громоздкости. Поэтому его реконструируют
в эпюр Монжа - чертеж, составленный из
двух или трех связанных между собой
ортогональных проекций геометрической
фигуры.
Преобразование
пространственного макета в эпюр
осуществляется путем совмещения
плоскостей П1
и П3
с фронтальной плоскостью проекций
П2.
Для
совмещения плоскости П1
с П2
поворачиваем П1
на 90° вокруг оси x
в
направлении движения часовой стрелки
(см. рис. 29).
Для
совмещения П3
с П2
поворачиваем П3
вокруг оси z
также
на угол 90° в направлении, противоположном
движению часовой стрелки. При повороте
будет перемещаться и ось у,
которая распадается на две оси (у и у3).
После
совмещения плоскостей проекций
пространственный макет примет вид,
показанный на рис. 30.
Обычно
не указывают обозначение полуплоскостей
проекций и отрицательное направление
осей. Тогда, в окончательном варианте,
эпюр принимает вид, показанный на рис.
31.
z;~y
z
П2[П,(П3)] П3[П2(П,)]
о
X
О
Уз
х;
-У
njnjnj]
Рис.
30
Рис.
31
21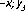
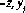
Точка
- одна из основных базовых понятий
геометрии. Для отображения этого
простейшего геометрического образа
на плоскости целесообразно понимать
под точкой физический объект, имеющий
линейные размеры. При этом условно
за точку принимают шарик с бесконечно
малым радиусом. При такой трактовке
понятия точки можно говорить о ее
проекциях.
Для
построения эпюра точки следует
руководствоваться первым инвариантным
свойством ортогонального проецирования:
«Проекция точки есть точка». Пусть даны
в пространстве точка А и три взаимно
перпендикулярные плоскости проекций
(рис. 32). В данном случае и в дальнейшем
для получения эпюра будем пользоваться
первым октантом системы плоскостей.
Спроецируем ортогонально точку А на
три плоскости проекций. Для этого в
соответствии с правилом проецирования
через точку А проводим последовательно
прямые линии, перпендикулярные к Пь
П2,
П3
- проецирующие лучи. В точках
пересечения этих лучей с плоскостями
проекций получаем ортогональные
проекции точки А. Назовем их: А\
- горизонтальная проекция, А2
- фронтальная проекция, А3
- профильная проекция. Каждая пара
из трех проецирующих лучей (АА\,
АА2,
АА3)
определяет плоскость, перпендикулярную
к двум плоскостям и к оси проекций. Эти
плоскости (Е, Е', Е"), называемые
проецирующими, пересекаются с плоскостями
проекций по двум взаимно перпендикулярным
прямым, имеющим
общие точки на осях проекций (соответственно
Ах,
Ау,
Ах).
Для
получения эпюра точки А
преобразуем пространственный макет,
изображенный на рис. 32, по схеме,
предложенной выше.
На
эпюре (рис. 33) проекции точки будут
располагаться на прямых, перпендикулярных
к осям проекций и проходящих через
точки Ах,
Ау,
Ах.
Z
Z
X
Рис.
32
Рис.
33
22Проекции точки
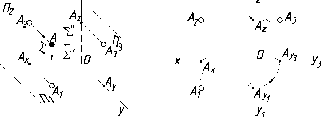


Эти
прямые, являющиеся проекциями
соответствующих проецирующих лучей,
называют линиями проекционной связи.
Горизонтальная
(А1)
и фронтальная (А2)
проекции будут располагаться на
общей вертикальной линии связи, а
фронтальная и профильная (Аз) на общей
горизонтальной линии. Для связи
горизонтальной и профильной
проекций можно воспользоваться дугой
окружности, проводимой из точки 0;
также можно на горизонтальной линии
связи отложить от оси z
вправо
отрезок AZA3,
равный
AXAi.
Прямоугольные
координаты точки
А?о
Уз
Система
трех взаимно перпендикулярных
плоскостей проекций ана-
логична
декартовой системе координатных
плоскостей. При этом оси про-
екций
соответствуют осям координат с началом
в точке 0.
ось x
-
оси аб-
цисс, ось у
-
оси ординат, ось z
-
оси аппликат.
Исходя
из этого, положение точки в пространстве
может быть опре-
делено
тремя координатами: х,
у, z.
Координата
точки - число, выражаю-
щее величину
расстояния от точки до
соответствующей
плоскости проек-
ций.
Анализируя
эпюр (рис. 34),
можно
отметить, что каждая из проек-
ций
точки А определяется двумя коор-
динатами
этой точки: А1
- x
и
у,
А2
- x
и
z,
А3
- у
и z.
Из
этого следует, что положение
точки
в пространстве вполне опреде-
ляется
положением ее двух ортого-
нальных
проекций.
Точка
в октантах пространства
На
рис. 29 было показано, что плоскости
координат в своем пересечении
образуют восемь трехгранных углов -
восемь октантов.
Зная
положительное и отрицательное
направление осей, по координатам
точки можно также определить, в каком
октанте расположена точка:
■7 |
|
Ах ^ |
А |
г Ха |
|
|
Знаки координат |
Октанты |
Знаки координат |
||||||
x |
у |
z |
x |
у |
z |
||||
I |
+ |
+ |
+ |
V |
- |
+ |
+ |
||
II |
+ |
- |
+ |
VI |
- |
- |
+ |
||
III |
+ |
- |
- |
VII |
- |
- |
- |
||
IV |
+ |
+ |
- |
VIII |
- |
+ |
- |
||
23
На
рис. 35а, показаны точки Л,
В, С,
расположенные в разных октантах, и
их эпюры (рис. 35 б), соответствующие
этому расположению.
б)
Рис.
35
IА2
Безосный
чертеж
Большинство
задач начертательной геометрии решают,
не устанав-
ливая метрической связи
с плоскостями проекций. Вследствие
этого по-
строения
на чертеже можно выполнять в безосной
системе
плоскостей проекций, т.е.
без указания положения осей
(рис.
36). Имея такой чертеж, можно, при
необходимости,
всегда ввести оси и
тем самым задать расстояние от точки
до
условно выбранных плоскостей П1
и П2.
Иными словами,
для безосного чертежа
(эпюра) плоскости проекций прини-
маются
неопределенными, т.е. могут перемещаться
парал-
лельно
самим себе.
Механизм
такого пе-
ремещения иллюстри-
рует
рис. 37.
Перенесение
оси
на
чертеже вверх или вниз соответст-
вует
параллельному переносу в про-
странстве
двугранного угла ЩП2
в но-
вое положение (П'1П'2)
в направлении
биссекторной плоскости
0. Биссек-
торной называют плоскость,
прохо-
дящую через ось проекций и
делящую
двугранный угол пополам.
0/4;
Рис.
36
24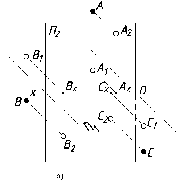
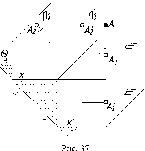
а
эп ре тако у параллельно у переносу
двугранного угла соответствует
перемещение начала координат - точки
0
по постоянной чертежа к,
которая
является следом биссекторной плоскости
(рис. 38).
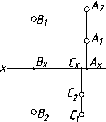
Рис.
39 демонстрирует построение на безосном
чертеже профильной проекции точки : по
заданным горизонтальной и фронтальной
ее проекциям.
Построение
выполнено с помощью постоянной чертежа
к,
проведенной в случайном месте чертежа
под углом 45° к направлению линии связи
::i.
Рис.
38 Рис. 39
Конкурирующие
точки
Геометрические
образы могут быть взаимно расположены
таким образом, что некоторые из них
(или отдельные их части) будут закрыты
от наблюдателя.
Построение
границы видимости образов на чертеже
выполняются на основании выявления и
анализа конкурирующих точек.
Конкурирующими
называют точки, лежащие на одном
проецирующем луче.
Для
определения видимости конкурирующих
точек рассуждают следующим образом
(рис. 40). Точки : и В лежат на общем
горизонтально - проецирующем луче, т.е.
их горизонтальные проекции совпадают.
Точка : выше точки В и расположена ближе
наблюдателю (г.о. всегда находится между
наблюдателем и соответствующей
плоскостью проекций). Следовательно,
она будет видна, а точка В закрыта ею.
Из двух совпадающих проекций :1
и В1
проекцию В1
невидимой точки В заключают в скобки.
На
П2
точки : и В проецируются разными лучами,
поэтому фронтальные проекции их не
совпадают. Обе точки относительно П2
видны.
25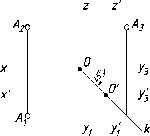
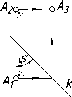
На
эпюре (рис. 41) вопрос видимости точек А
и В относительно Пь
принимая во внимание вышеуказанные
рассуждения, решают по удалению их
фронтальных проекций (А2
и В2)
от оси х.
Фронтальная
проекция точки А2
расположена от оси дальше, чем проекция
В2,
следовательно, горизонтальную проекцию
В\
точки В заключаем в скобки.
Аналогично
рассуждают, определяя видимость
конкурирующих точек и относительно
других плоскостей проекций (рис. 42).
На
рис. 42 показаны фронтально-конкурирующие
точки Си D,
а
также профильно-конкурирующие точки
Е
и F.
*
Аг(В,)
Рис.
40
Рис.
41
c2=(d2)
О
Z
f3JE3)
♦
Ус>Уо
Fl
Е) у1 XF>XE
Рис.
42
26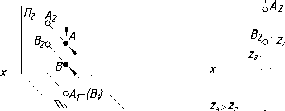
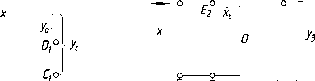
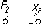
Наряду
с точкой, прямая линия является одним
из исходных понятий в геометрии. Прямая
является простейшей из линий (более
подробно линии будут рассмотрены в
разделе V), которой в начертательной
геометрии отводится важная роль при
решении инженерных задач.
Аналитически
прямую в пространстве можно задать
разными способами. Например, как
уравнение прямой, полученной при
пересечении двух плоскостей: Aix
+
Biy
+ Ciz
+
Di
=
0
A2x
+
B2y
+
C2z
+
D2
=
0 Другим,
более удобным, является уравнение
прямой, проходящей
через
две заданные точки Mi
(xi yi
zi) и
M2
(x2
y2
z2)
x
- xi
= y-
yi
= z
- zi
x2
-
xi y
2
-
yi z2
-
zi
Если
рассматривать прямую на плоскости, то
общим уравнением ее будет: Ax
+ By
+ C
= 0.
При
построении эпюра прямой следует
использовать третье свойство
проецирования: «Проекция прямой есть
прямая». Другими словами, для определения
проекции прямой достаточно задать
проекции двух не тождественных
точек, принадлежащих этой прямой.
Рис.
43
Пусть
прямая l
проходит
через две точки A
и
В
(рис. 43 а). На эпюре этой прямой (рис. 43
б) разность расстояний точек В и A
прямой
до горизонтальной плоскости проекций
П1
определяется величиной zB
-
zA,
равной
разности аппликат точек В и A.
Разность
расстояний точек В и A
до
фронтальной плоскости проекций П2
определяется разностью ординат yB
-
yA.
И,
наконец, разность расстояний точек A
и
В до профильной плоскости проекций П3
определяется величиной разности абсцисс
xA
-
xB.
27Проекции прямых линий
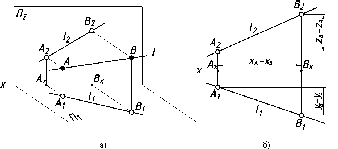
Прямая
линия общего положения
акая
пря ая зани ает в систе е плоскостей
проекций произвольное положение (углы
наклона прямой к плоскостям П1,
П2,
П3
- отличные от 0 и 90°). Для этой прямой: zB
-
zA
Ф
0
/Б
- /Л Ф
0 (I)
Хд
- Хб Ф
0
На
эпюре прямой общего положения (см.
рис.43 б) нет натуральной величины отрезка
и углов его наклона к плоскостям
проекций.
Частные
случаи расположения прямой
Прямая
линия, кроме произвольного, может
занимать следующие положения относительно
плоскостей проекций:
параллельное
одной из плоскостей проекций (прямые
уровня);
перпендикулярное
какой-нибудь плоскости проекций
(проецирующие прямые).
Прямые
уровня
Прямые
линии, параллельные (но не перпендикулярные)
плоскостям проекций, называют линиями
уровня. Таких линий три:
горизонталь
- прямая параллельная П1,
фронталь
- прямая параллельная П2,
профильная
прямая, параллельная П3.
Рис.
44
Если
в условии (I) будем иметь: zB
-
zA
=
0, то прямая l
преобразуется
в горизонталь h
(рис.
44 а). Особенностью эпюра горизонтали
(рис. 44 б) является то, что ее фронтальная
проекция (h2)
параллельна
оси х, а горизонтальная проекция
(h1)
составляет
с осью х
угол р, равный углу наклона самой прямой
к плоскости проекций П2.
Горизонтальная проекция А1В1
от
28
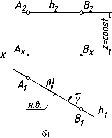
резка
прямой h
определяет
длину этого отрезка. Эта же проекция
выявляет угол (у) наклона прямой к
профильной плоскости проекций П3.
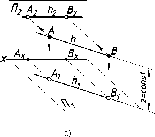
Если
в условии (I)
yB
-
yA
=
0, то прямая l
преобразуется
во фронталь f
(рис.
45 а). На эпюре фронтали (рис. 45 б) ее
горизонтальная проекция f
параллельна
направлению оси проекций. Фронтальная
проекция (f2)
составляет
с направлением оси х угол а, равный углу
наклона самой прямой к горизонтальной
плоскости проекций Пь
а с направлением оси z
-
угол у, равный углу наклона прямой к
П3.
Фронтальная проекция (A2B2)
отрезка
прямой f
определяет
длину этого отрезка (см. рис. 45 б).
Аналогично,
если в условии (I)
xA
-
xB
=
0, то прямая l
преобразуется
в профильную прямую р (рис. 46 а, б).
Особенность проекций профильной прямой
(см. рис. 46 б): отрезок прямой проецируется
без искажения на профильную плоскость
проекций A3B3.
Здесь
же видна натуральная величина углов
его наклона а и р. Проекции р1
и р2
прямой располагаются на одной линии
связи.
а)
Рис.
46
б)
29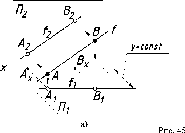
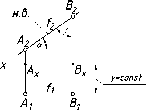
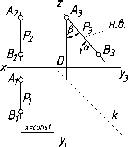
Проецирующие
прямые
Прямые
линии, перпендикулярные плоскостям
проекций, называют проецирующими.
Различают следующие проецирующие
прямые:
горизонтально-проецирующая,
перпендикулярная П1;
фронтально-проецирующая,
перпендикулярная П2;
профильно-проецирующая,
перпендикулярная П3.
Проецирующие
прямые в тоже время параллельны двум
координатным плоскостям проекций.
Если
в условии (I) для прямой общего положения
1
ввести xA
-
xB
=
0 и yB
-
yA
=
0,
то она преобразуется в горизонтально-проецирующую
прямую (рис. 47). Фронтальная и профильная
проекция отрезка этой прямой А2В2
определяет его натуральную длину, а
горизонтальная проекция А1В1
преобразуется
в точку. Эта прямая одновременно является
фронтальной и профильной прямой.
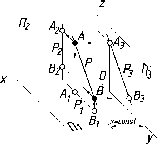
Если
в условии (I) примем xA
-
xB
=
0 и zB
-
zA
=
0, то прямая l
преобразуется
во фронтально-проецирующую прямую
(рис. 48). Здесь гори-
Л
А
о
12°А2)=В2
9В2
х
X
0
/;
о
Рис.
47
Рис.
48
А
2 н.6.
В2
Z
зонтальная
(профильная) проекция А1В1
определяет длину отрезка АВ
прямой 1, а фронтальная
проекция
преобразуется в точку. Эта прямая
является одновременно горизонтальной
и профильной прямой.
О
И,
наконец, если в условии (I)
Рис.
49
то
прямая 1
преобразуется в про- фильно-проецирующую
прямую (рис. 49). Горизонтальная и
30
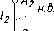
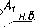
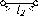
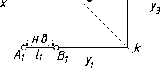

фронтальная
проекции прямой параллельны оси х и
каждая из проекций определяет длину
отрезка. На П3
проекция прямой - точка. Эта прямая
одновременно является горизонталью
и фронталью.
Понятие
о следах прямой
Точки
пересечения прямой линии с координатными
плоскостями проекций называют следами
прямой. Соответственно точку пересечения
прямой с горизонтальной плоскостью
проекций П1
называют горизонтальным следом, а
с фронтальной плоскостью проекций П2
- фронтальным следом.
На
рис. 50 прямая 1
пересекает горизонтальную плоскость
проекций П1
в точке М, а фронтальную плоскость П2
в точке N.
Точка
М имеет аппликату zM
=
0, т.е. след М совпадает с М1,
а М2
лежит на оси х.
Точка
N
прямой
имеет ординату yN
=
0,
след N
совпадает
с N2,
а
N\
лежит
на оси х.
Построение
следов на эпюре показано на рис. 51.
Рис.
50 Рис. 51
Чтобы
найти горизонтальный след М, необходимо
найти сначала его фронтальную проекцию
М2
как точку пересечения фронтальной
проекции прямой 12
с осью х. Горизонтальная проекция М\
совпадает с горизонтальным следом
М и лежит на продолжении 1\.
Чтобы
найти фронтальный след N,
необходимо
найти сначала его горизонтальную
проекцию N1
как
точку пересечения 1\
с осью х. Фронтальная проекция следа
N
(N2)
будет
лежать на продолжении 12
и совпадает с фронтальным следом N.
Если
прямая параллельна плоскости проекций,
то следом ее на этой плоскости является
несобственная точка.
31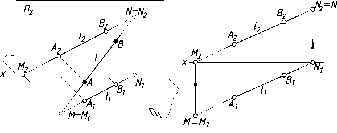
На
эпюре натуральная длина отрезка прямой
и углы его наклона видны только в случае
его частного расположения относительно
плоскостей проекций.
Если
же прямая занимает общее положение
относительно плоскостей проекций,
то для нахождения натуральной величины
отрезка этой прямой и углов его наклона
к плоскостям проекций можно использовать
соответствующее свойство ортогонального
проецирования.
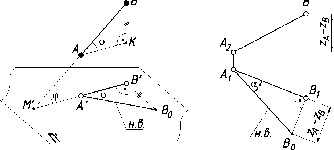
Используя
это свойство, на плоскости проекций П'
(рис. 52), можно построить прямоугольный
треугольник, один катет которого -
проекция отрезка АВ на плоскости П'
(А'В'),
а другой - разность расстояний концов
отрезка от плоскости проекций (В'В0
= ВК).
Гипотенуза такого треугольника
(А'В0)
будет равна натуральной величине
отрезка. Из рис. 52 видно также, что
угол В'А'В0
равен углу ВАК
и будет определять угол наклона прямой
к плоскости Пь
Аналогичные
построения можно выполнить на эпюре
прямой
Принимаем
плоскость П' за П1
(горизонтальную плоскость проекций).
На горизонтальной проекции прямой, как
на катете, строим прямоугольный
треугольник. Второй катет этого
треугольника равен разности расстояний
концов отрезка от П1
(zB
-
zA).
В
результате получаем прямоугольный
треугольник А1В1В0,
гипотенуза которого равна натуральной
величине отрезка АВ,
а угол а есть угол наклона отрезка к
горизонтальной плоскости проекций П1.
(рис.53).
В
в2
Рис.
52
Рис.
53
32Натуральная длина отрезка прямой и углы его наклона к плоскостям проекций
Аналогичные
построения можно выполнить, принимая
плоскость П' за фронтальнyю плоскость
проекций П2
(рис. 54).
Такой
прием нахождения натуральной величины
отрезка прямой общего положения и
углов его наклона к плоскостям проекций
называют способом прямоугольного
треугольника.
Взаимное
расположение двух прямых
Две
прямые в пространстве могут пересекаться,
быть параллельны друг другу или
скрещиваться.
Пересекающиеся
прямые.
Прямые линии, имеющие общую точку,
называются пересекающимися.
Рис.
55 Рис. 56
33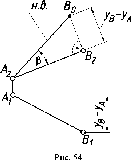
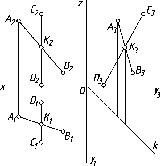
Если
прямые пересекаются в пространстве,
то их одноименные проекции также
пересекаются, и точки пересечения
проекций лежат на одной линии связи.
Для подтверждения пересечения прямых
на чертеже бывает достаточно двух
проекций (рис. 55). Однако, если хотя бы
одна из прямых является линией уровня,
то одной из двух проекций должна быть
проекция на ту плоскость, которой
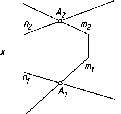
параллельна эта линия уровня (рис. 56).
Параллельные
прямые.
Прямые линии, пересекающиеся в
несобственной точке, называются
параллельными.
Если
две прямые параллельны в пространстве,
то их одноименные проекции тоже
параллельны. Для подтверждения
параллельности прямых m
и
n
достаточно
параллельности двух одноименных
проекций (рис. 57). Исключение составляют
некоторые прямые частного положения.
Например, для подтверждения
параллельности профильных прямых
необходимо проверить параллельность
всех трех одноименных проекций прямых.
Так, показанные на рис. 58 профильные
прямые CD
и
AB
после
построения профильной проекции
оказываются не параллельными друг
другу.
Скрещивающиеся
прямые.
Прямые, не пересекающиеся и не
параллельные между собой, называются
скрещивающимися. На рис. 59 показана
пространственная модель таких прямых.
Если
прямые скрещиваются в пространстве,
то на эпюре их одноименные проекции
могут пересекаться, но точки их
пересечения не лежат на одной линии
связи (не являются проекциями одной
точки) (рис. 60). Так, точка пересечения
фронтальных проекций скрещивающихся
прямых m
и
n
является
фронтальной проекцией двух точек M
и
K,
принадлежащих
соответственно прямым m
и
n.
Эти
точки не совпадают, так как имеют разные
ординаты.
Аналогично,
точка пересечения горизонтальных
проекций mi
и
ni
является
горизонтальной проекцией двух точек
Е
и F,
имеющих
разные аппликаты.
X
У1
Рис.
57
Рис.
58
34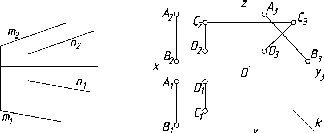
Точки
пересечения одноименных проекций
скрещивающихся прямых являются
конкурирующими. Их видимость на эпюре
определяют, как и видимость любых
конкурирующих точек, по величине
удаления от плоскости, на которой
их проекции совпадают. Невидимые точки
условно заключают в скобки.
Рис.
59 Рис. 60
Наряду
с точкой и прямой, плоскость также
относится к основным
базовым понятиям
в начертательной геометрии.
Плоскость
является простейшей поверхностью.
Между декартовыми
координатами
принадлежащих ей точек существует
зависимость, аналити-
чески выраженная
в форме многочлена первой степени:
Ax
+
By
+
Cz
+
D
=
0,
т.е.
плоскость - поверхность первого
порядка.
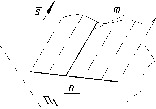
Кинематическое
образование
плоскости, как простейшей
поверх-
ности, может быть
представлено
(рис. 61) перемещением
прямой m
(образующей)
параллельно направ-
лению 5
по неподвижной прямой n
(направляющей).
Положение
плоскости в про- рис. 61
странстве
однозначно определяется
тремя
различными точками (А,
В, С),
не принадлежащими одной прямой. Поэтому
для задания плоскости на чертеже
достаточно указать проекции:
35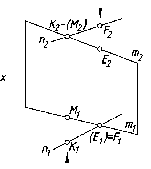
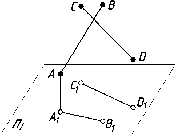
Проекции плоскости
трех
различных точек, не принадлежащих
одной прямой (рис.62 z);
прямой
и
точки
вне ее (рис.
62 [);
двух
прямых, пересекающихся в
собственной (рис. 62 в) или в
не-
собственной (рис. 62 г) точке;
отсека
плоской фигуры (рис. 62 д).
Ву
б
В
1
а) б) в) г) д)
Рис.
62
В
некоторых случаях бывает целесообразным
задавать плоскость прямыми, по которым
эта плоскость пересекает плоскости
проекций. Такой вариант задания
плоскости называют заданием плоскости
следами.
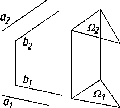
На
рис. 63 показана плоскость Р и ее следы
на плоскостях проекций. При этом
различают:
Р\
- горизонтальный след плоскости Р;
Р2
- фронтальный след плоскости Р;
Р3
- профильный след плоскости Р.
Рис.
63
36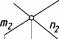
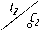
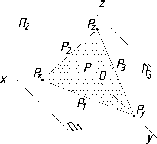
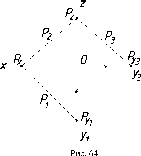
Точки
PX,
PY,
PZ,
в
которых пересекаются два следа, называют
точками схода следов. Точки схода
следов всегда располагаются на осях
проекций. На рис. 64 представлен эпюр
плоскости, заданной следами.
Всегда
можно перейти от одного вида задания
плоскости к любому другому. Например,
на рис. 65 показано, как от задания
плоскости двумя пересекающимися прямыми
(a
@
b)
можно
перейти к заданию ее следами (Р\,
Р2).
Для этого достаточно найти горизонтальные
следы М
и М
двух заданных прямых, а также фронтальные
следы этих прямых N
и
N.
Соединив
проекции М\
и М\,
а также N2
и
N2,
получим соответственно горизонтальный
(Pi)
и
фронтальный (Р2)
следы плоскости Р.
Плоскость
общего положения
На
приведенных выше примерах заданная
плоскость занимает произвольное
положение по отношению к плоскостям
проекций (углы наклона этой плоскости
к плоскостям проекций отличны от 0° к
90°). Такая плоскость называется плоскостью
общего положения.
На
эпюре такой плоскости не сохраняются
метрические характеристики плоской
фигуры и не видны углы наклона ее к
плоскостям проекций.
Частные
случаи расположения плоскости
Кроме
рассмотренного общего случая плоскость
по отношению к плоскостям проекций
может занимать следующие положения:
перпендикулярное
одной из плоскостей проекций (проецирующие
плоскости);
параллельное
одной плоскости проекций (плоскости
уровня).
37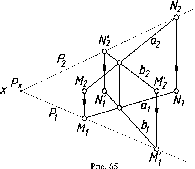
Проецирующие
плоскости
Плоскости,
перпендикулярные одной из плоскостей
проекций, называют проецирующими.
При этом различают три типа проецирующих
плоскостей:
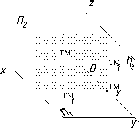
горизонтально-проецирующая,
перпендикулярная П1
(рис. 66
а);
фронтально-проецирующая,
перпендикулярная П2
(рис. 67 а);
профильно-проецирующая,
перпендикулярная П3
(рис. 68
а).
Рис.
66
Характерной
особенностью проецирующих плоскостей
является то, что сами плоскости и любые
геометрические фигуры, лежащие в них,
проецируются на перпендикулярные
таким плоскостям плоскости проекций
в виде прямых линий. Такое свойство
проекций проецирующих плоскостей
называется собирательным.
38
а)
Рис.
67
б)
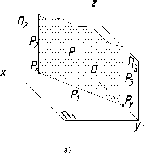
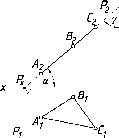
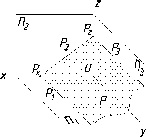
Например,
на рис. 66
горизонтально-проецирующая плоскость,
заданная двумя следами - горизонтальным
(Pi)
и
фронтальным (Р2),
может быть задана только одним следом
- Р1.
Именно этот след несет всю информацию
о заданной плоскости.
Проецирующие
плоскости на эпюре удобнее задавать
следами. При этом след (проекция),
обладающий собирательным свойством,
несет информацию об углах наклона
проецирующей плоскости к неперпендикулярным
ей плоскостям проекций (рис. 66
б - 68
б). Два других ее следа перпендикулярны
той же плоскости проекций, какой
перпендикулярна сама плоскость. Эти
два следа не играют важной роли в
определении плоскости, поэтому на
безосном чертеже проецирующие плоскости
обычно задают одним следом - линией
пересечения только с той плоскостью,
которой они перпендикулярны.
а) б)
Рис.
68
Плоскости
уровня
Плоскости,
параллельные какой-либо плоскости
проекций, называют плоскостями уровня.
Различают три типа таких плоскостей:
горизонтальная
плоскость уровня, параллельная П1
(рис. 69);
фронтальная
плоскость уровня, параллельная П2
(рис. 70);
профильная
плоскость уровня, параллельная П3
(рис.71).
Характерной
особенностью таких плоскостей является
то, что плоские фигуры, расположенные
в них, проецируются без искажения на
ту плоскость проекций, которой плоскости
уровня параллельны. Две другие проекции
(следы) плоскости уровня - прямые,
параллельные соответствующим
осям проекций. На безосном чертеже
обычно задают плоскости уровня одним
(любым) следом.
39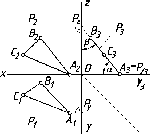

Рис.
71
40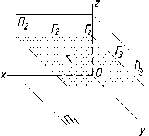
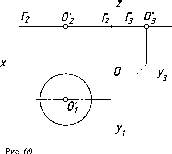
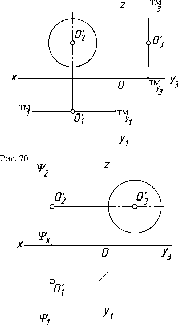
Показать
на чертеже точку (или прямую), принадлежащую
плоскости, занимающей общее положение
в системе плоскостей проекций,
произвольно, не связывая ее с другими
элементами плоскости, невозможно.
Поэтому точка в плоскости выбирается
из условия, что она находится на прямой
линии этой плоскости.
Прямая
же линия принадлежит плоскости, если
она проходит:
через
две точки этой плоскости;
через
одну точку плоскости и параллельно
какой-нибудь прямой этой плоскости.
а) б)
Рис.
72
Рис.
72 иллюстрирует вышеизложенные условия
принадлежности прямой плоскости на
чертеже.
Прямая
1
(см. рис. 72 а) принадлежит S
(а
@ b),
так
как проходит через две точки Л и В,
выбранные на прямых а
и b
этой
плоскости. На рис. 72б используется
другое условие: прямая l
имеет
общую точку Л с плоскостью S
(а
@ b)
и
параллельна прямой b,
лежащей
в этой плоскости. Оба рисунка
демонстрируют также принадлежность
точки K
плоскости
S
вследствие
принадлежности ее прямой 1.
Случай
принадлежности прямой и точки плоскости,
заданной следами, представлен на
рис. 73. Здесь общими
точками прямой и плоскости являются
следы прямой Ми
N,
принадлежащие
соответствующим следам плоскости.
41Взаимное расположение простейших геометрических образов
Принадлежность прямой и точки плоскости
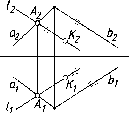
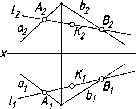
Принадлежность
точек и прямых линий плоскостям,
занимающим частное положение, определяется
собирательным свойством их проекций.
Так, ниже приведены фронтально-проецирующая
плоскость Р (рис. 74 а) и горизонтальная
плоскость уровня Г (рис. 74 б), а также
показаны точка K
и
линия 1,
лежащие в этих плоскостях.
/о Г2
к.
16
Рис.
74
Главные
линии плоскости
Главными
называют следующие линии плоскости:
прямые,
принадлежащие плоскости и параллельные
какой-либо плоскости проекций, - линии
уровня;
прямые,
принадлежащие плоскости и перпендикулярные
какой- нибудь из линий уровня, - линии
наибольшего наклона плоскости к
плоскостям проекций.
42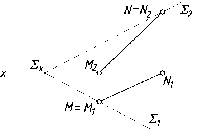
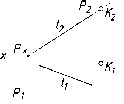
Линии
уровня в плоскости
В
заданной плоскости, как и в пространстве,
можно выделить три типа линий уровня:
горизонталь
плоскости, линия параллельная П1;
фронталь
плоскости, линия параллельная П2;
профильная
прямая плоскости, линия параллельная
П3.
На
рис.75 показаны горизонталь h,
фронталь
f
и
профильная прямая р,
принадлежащие
плоскости S.
Из
рис. 75 видно также, что каждая из линий
уровня всегда параллельна соответствующему
следу плоскости :
горизонталь
(h)
-
горизонтальному следу плоскости (S1);
фронталь
(f)
- фронтальному следу плоскости (S2);
профильная
прямая (р) - профильному следу плоскости
(S3).
Исходя
из этого, следа плоскостей называют
оде линиями нулевого
/
1
0
л0 0\
уровня
(h
,
f
,
p
).
Рис.
76 иллюстрирует задание линий уровня
плоскости на чертеже.
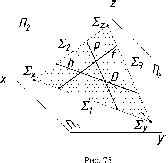
В
плоскостях частного положения некоторые
из линий уровня становятся проецирующими
прямыми. Так (рис. 77 а), в горизонтально-
проецирующей плоскости 0
фронталь f
и
профильная прямая р
займут го- ризонтально-проецирующее
положение, а в горизонтальной плоскости
уровня Г (рис. 77 б) фронталь f
станет
профильно-проецирующей прямой, а
профильная прямая р
- фронтально-проецирующей прямой.
43
^ I |
|
r |
|
" ' ? |
|
f°
T1
Пл
Рис.
76
44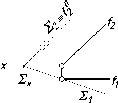
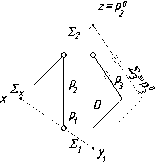
Рис.
77
Линии
наибольшего наклона плоскости
Другой
разновидностью главных линий плоскости
являются линии наибольшего наклона
плоскости к плоскостям проекций. Для
плоскостей общего положения это всегда
прямые общего положения.
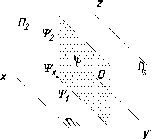
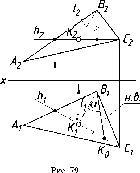
На
рис. 78 показана линия (1)
наибольшего наклона плоскости S
к
горизонтальной плоскости проекций
(П1),
которую иногда называют линией
наибольшего ската плоскости. Отличительной
особенностью этой линии является
перпендикулярность ее к горизонтали
(или горизонтальному следу) плоскости.
Аналогично
на эпюре (рис. 79) горизонтальная проекция
линии наибольшего ската (1\)
перпендикулярна горизонтальной проекции
горизонтали (А).
45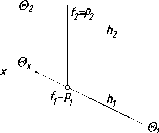
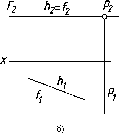
Для
линии наибольшего наклона плоскости
к П2
характерно, что ее фронтальная проекция
перпендикулярна к фронтальной проекции
фронта- ли (или фронтальному следу). И,
наконец, профильная проекция линии
наибольшего наклона к П3
займет положение, перпендикулярное к
профильной проекции профильной
прямой плоскости.
Из
рис. 79 видно, что линиями наибольшего
наклона можно пользоваться для
определения угла наклона плоскости к
плоскостям проекций. Здесь с помощью
способа прямоугольного треугольника
определена натуральная величина
линии наибольшего наклона l
=
\B1K0\
и
угол ее наклона к плоскости Пь Этот же
угол определяет наклон и самой плоскости
S
(ЛВС)
к П1
(см. рис.78).
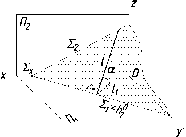
Прямая
параллельна плоскости, если она
параллельна какой-либо прямой, лежащей
в этой плоскости. Через заданную точку
в пространстве можно провести бесчисленное
множество прямых линий, параллельных
заданной плоскости. Для получения
единственного решения требуется задать
дополнительное условие - определить
прямую, принадлежащую плоскости. Так,
на рис. 80 показана прямая а, которая
параллельна плоскости S,
так
как она параллельна прямой а'этой
плоскости.
Рис.
80 Рис. 81
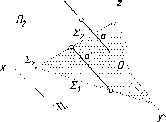
Условие
параллельности прямой и плоскости на
эпюре иллюстрирует рис. 81. Здесь
прямая l
параллельна
плоскости S
(□
ЛВС),
так как выдержано условие параллельности
ее одной из сторон треугольника - ЛВ.
Параллельность линии l
и
ЛВ подтверждается параллельностью их
одноименных проекций на эпюре.
46
Параллельность прямой и плоскости, параллельность плоскостей


Случай
параллельности прямой плоскости при
задании плоскости следами показан для
плоскости общего положения (рис. 82 а) и
частного положения (рис. 82 б).
а) б)
Рис.
82
Плоскости
взаимно параллельны, если две
пересекающиеся прямые одной плоскости
соответственно параллельны двум
пересекающимся прямым другой
плоскости.
Такими
пересекающимися прямыми могут быть:
произвольные
прямые плоскости (рис. 83 а);
следы
плоскостей (рис. 83 б).
а) б)
Рис.
83
47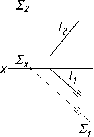
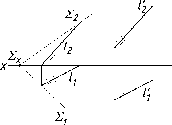

На
рис. 84 а показаны две параллельные
плоскости S
и
S'.
Их
параллельность определяется на
эпюре параллельностью соответствующих
проекций пересекающихся прямых: m1
||
т\,
п1
|| п\,
m2
||
m2,
n2
||
n2.
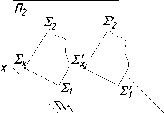
На
рис. 84 б показан случай параллельности
двух плоскостей при задании их
следами. Здесь параллельность плоскостей
обеспечивает параллельность их
одноименных следов: Si
||
S'i;
S21|
S
'2.
а) б)
Рис.
84
Перпендикулярность
прямой и плоскости
Прямая
перпендикулярна плоскости, если она
перпендикулярна двум пересекающимся
прямым этой плоскости (рис. 85 а).
Перпендикуляр
к плоскости общего положения это всегда
прямая общего положения, поэтому для
подтверждения перпендикулярности этой
прямой и плоскости на чертеже в качестве
двух пересекающихся прямых плоскости
выбираются линии уровня. В соответствии
с вышеизложенным прямой угол проецируется
в натуральную величину на П1
между прямой и горизонталью, а на П2
- между прямой и фронталью плоскости.
Следовательно,
на чертеже: (рис. 85 б) горизонтальная
проекция перпендикуляра к плоскости
перпендикулярна горизонтальной проекции
горизонтали плоскости, а фронтальная
- перпендикулярна фронтальной проекции
фронтали плоскости.
48

Перпендикулярность прямой и плоскости, перпендикулярность плоскостей
а) б)
Рис.
85
На
рис. 86
показан случай перпен-
дикулярности
прямой к плоскости обще-
го положения
при задании плоскости
следами. Здесь
прямая 1
перпендикулярна
плоскости S
(Si, S2),
так
как она перпен-
дикулярна следам
плоскости, которые
являются
горизонталью и фронталью ну-
левого
уровня.
Рис.
86
Перпендикулярность
двух плоскостей
Две
плоскости взаимно перпендикулярны,
если одна из них проходит через
перпендикуляр к другой.
Как
видно из рис. 87, через перпендикуляр к
плоскости можно провести бесчисленное
множество плоскостей, перпендикулярных
данной. Поэтому для однозначного решения
требуется задать дополнительные
условия. Так, на рис. 88
для для построения на чертеже плоскости,
перпендикулярной заданной S
(h
@
f),
введена
прямая а,
пересекающая перпендикуляр к
плоскости S
-
1.
Новая плоскость 0 здесь будет задана
проекциями пересекающихся прямых а и
1, и она перпендикулярна S,
так
как проходит через перпендикуляр (1)
к ней.
49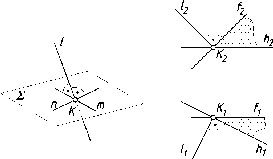
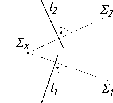
Рис.
87 Рис. 88
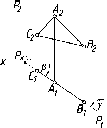
На
рис. 89 показан случай перпендикулярности
двух плоскостей Р и 0 общего положения
при задании их следами. Здесь
перпендикулярность плоскостей
определяется прямой 1,
принадлежащей плоскости 0
и перпендикулярной плоскости Р (11
± Р1;
12
± Р2).
Следует
запомнить: две плоскости общего положения
не перпендикулярны между собой, если
они заданы взаимно перпендикулярными,
одноименными следами, так как в
плоскости нет прямой, перпендикулярной
другой плоскости.
Рис.
90 иллюстрирует перпендикулярность
плоскости общего положения S
(S1,
S2)
и
фронтально-проецирующей плоскости 0
(01,
02).
Рис.
89
50
Рис.
90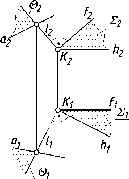
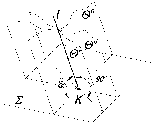

налитическое
ре ение задачи о пря ой, пересека ей
плоскость, сводится к решению системы
уравнений с тремя неизвестными. Допустим,
что плоскость S
задана
уравнением:
A1x
+
B1y
+
C1z
+
D1
=
0, а
прямая l
задана
совокупностью двух уравнений
A2X
+
В2У
+ C2Z
+
D2
=
0
и A3X
+
Взу + C3Z
+
D3
=
0.
Координаты
точки пересечения прямой l
с
плоскостью S
определяются
в результате совместного решения этих
трех уравнений.
При
аналитическом решении задачи о
пересечении двух плоскостей, заданных
общими уравнениями, получают общее
уравнение прямой линии:
JA1x
+
В1у
+ C1z
+
D1
=
0,
IA2X
+
В2У
+ C2Z
+
D2
=
0.
Вопрос
может состоять только лишь в переводе
этой совокупности общих уравнений в
каноническое уравнение прямой.
Графическое
решение позиционных задач на пересечение
простейших геометрических образов
в общем случае включает в себя построение
либо точки встречи прямой с плоскостью,
либо линии пересечения двух плоскостей.
При этом линия пересечения плоскостей
однозначно определяется двумя
точками. Таким образом, в конечном итоге
задачи на пересечение сводятся к
нахождению точек (одной или двух), общих
для обоих пересекающихся геометрических
образов, и выявлению видимости этих
образов относительно друг друга.
При
построении таких общих точек
важную роль играет расположение
геометрических образов относительно
плоскостей проекций. Так, если
плоскость,
с которой пересекается либо прямая,
либо другая плоскость, занимает
частное положение, то общая точка
(линия) легко находится в чертеже
без дополнительных построений (рис. 91
а, б).
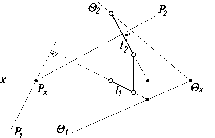
Здесь
искомыми являются точка D,
фронтальная
проекция которой определяется при
пересечении следа ©2
плоскости 0
с фронтальной проекцией прямой l
(см.
рис. 91 а), и линия 12, горизонтальная
проекция которой определяется точками
пересечения следа ©1
плоскости © с горизонтальными
проекциями прямых ЛВ
и СВ
(см. рис. 91 б).
При
определении видимости условно считается,
что заданная проецирующая плоскость
непрозрачна, поэтому видимым будет то,
что находится перед ней (см. рис. 91
б) и над ней (см. рис. 91 а). Стрелкой на
чертеже показано направление взгляда
на ту плоскость проекций, видимость на
которой определяется. На плоскости
проекций, которой заданная плоскость
перпендикулярна, видимость уже
определена, так как плоскость проецируется
в прямую и ничего от наблюдателя не
закрывает.
51Пересечение прямой и плоскости, пересечение плоскостей
а) |
|
б) |
|
Рис. 91 |
|
В
случае, когда пересекающиеся геометрические
образы (в частности, плоскости)
занимают общее положение относительно
плоскостей проекций, нахождение
точек (линий) пересечения без дополнительных
построений невозможно.
При
решении таких задач применяют один из
наиболее распространенных в
начертательной геометрии способов -
способ вспомогательных секущих
плоскостей. Этот способ является частным
случаем общего способа вспомогательных
секущих поверхностей, так как плоскость
можно рассматривать как простейшую
поверхность. Способ вспомогательных
секущих поверхностей более полно
будет рассмотрен далее.
Сущность
способа вспомогательных секущих
плоскостей заключается в том, что в
системе плоскостей проекций с заданными
геометрическими образами вводятся
дополнительные вспомогательные секущие
плоскости. Такие плоскости пересекают
заданные г.о. и позволяют с помощью ряда
построений выявить общие для обоих
образов точки. В качестве секущих
удобно использовать плоскости частного
положения, пересечение с которыми
определить, как было показано ранее,
достаточно просто.
Рассмотрим
алгоритм применения способа вспомогательных
секущих плоскостей на примере решения
следующих задач:
пересечение
прямой линии с плоскостью общего
положения;
пересечение
двух плоскостей общего положения;
анализ
взаимного положения прямой и плоскости,
двух плоскостей.
52
Пересечение
прямой линии с плоскостью общего
положения
При
решении этой задачи необходимо построить
точку, одновремен-
но принадлежащую
прямой и плоскости, и определить
видимость прямой
относительно
плоскости.
Алгоритм
решения задачи следующий:
через
заданную прямую проводят вспомогательную
секущую
плоскость;
строят
линию пересечения двух плоскостей -
секущей и заданной;
находят
общую точку построенной линии пересечения
с заданной
прямой;
определяют
видимость прямой относительно плоскости.
На
рис. 92 проиллюстрирован алго-
ритм
решения задачи. Здесь l
-
заданная
прямая, S
-
заданная плоскость, 0
- секущая
плоскость, m
-
линия пересечения секущей
плоскости
с заданной, D
-
искомая точка
пересечения прямой с
плоскостью.
Приведенный
алгоритм решения зада-
чи справедлив
и при выполнении построе-
ний на
эпюре. Однако следует обратить
внимание
на то, что вспомогательную секу-
щую
плоскость можно вводить как на Пь
так
и на П2.
На
рис. 93а через прямую l
проведена
горизонтально-проецирующая вспомогательная
секущая плоскость 0 (0i),
а
на рис. 93б через прямую l
проведена
фронтально-проецирующая вспомогательная
секущая плоскость 0 (02).
Результат решения не будет зависеть
от того, какой секущей плоскости
отдано предпочтение. На рис. 93 видимость
прямой не рассматривается.
Рис.
93
53
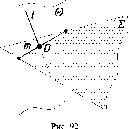
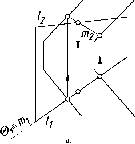
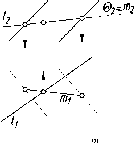
Примеры
построения точки пересечения прямой
линии
с
плоскостью общего положения
На
рис. 94 задана прямая 1
и плоскость общего положения S
(□
ABC).
В
качестве секущей выбрана
горизонтально-проецирующая плоскость
©(©i),
проходящая
через прямую 1.
Вспомогательная секущая плоскость
0(©i)
пересекает
данную плоскость S
(□
ABC)
по
линии т,
горизонтальная проекция которой
находится на следе секущей плоскости
©1.
Фронтальная проекция линии пересечения
строится по точкам, принадлежащим
соответственно фронтальным проекциям
сторон треугольника A2C2
и
A2B2.
На
фронтальной плоскости проекций
определится проекция D2
искомой
точки пересечения. Это есть точка
пересечения линии т2
с фронтальной проекцией заданной
прямой 12.
Горизонтальная проекция D1
лежит
на горизонтальной проекции прямой
11.
Для
определения видимости используот пары
конкурир^щих точек, принадлежащих
прямой 1
и скрещивающейся с ней стороной
треугольника. Видимость на
горизонтальной плоскости проекций
определяется по паре
горизонтально-конкурирующих точек 1,
2,
на фронтальной плоскости проекций - по
паре фронтально-конкурирующих точек
3, 4.
В
точке D
пересечения
прямой с плоскостью видимость прямой
будет меняться на противоположную.
54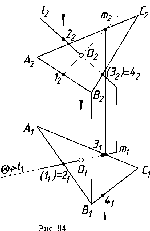
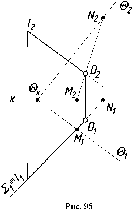
На
рис. 95 представлено построение точки
пересечения прямой с плоскостью,
заданной следами. Заданы прямая общего
положения l
и
плоскость 0(©1,©2).
Через прямую l
проведена
горизонтально- проецирующая плоскость
S
(S1),
которая
пересекает заданную плоскость © по
прямой MN.
Горизонтальная
проекция линии пересечения M1N1
совпадает
со следом секущей плоскости S1,
а
фронтальная проекция M2N2
определяется
по линиям проекционной связи. Фронтальная
проекция заданной прямой l2
пересекает
линию M2N2
в
точке D2.
Горизонтальная
проекция точки D
принадлежит
горизонтальной проекции данной прямой
l1.
Точка
D
принадлежит
как прямой, так и заданной плоскости и
является искомой точкой встречи прямой
l
с
плоскостью © (01,
©2).
Пересечение
двух плоскостей общего положения
При
решении этой задачи необходимо построить
линию пересечения плоскостей, которая
определяется двумя точками, и показать
видимость плоскостей относительно
друг друга. Алгоритм решения задачи
способом вспомогательных секущих
плоскостей следующий:
Определяется
первая точка искомой линии пересечения:
вводится
вспомогательная секущая плоскость,
рассекающая обе заданные;
строятся
линии пересечения секущей плоскости
с каждой из заданных плоскостей;
находится
точка пересечения построенных линий.
Аналогично
определяется вторая точка искомой
линии пересечения.
Показывается
видимость плоскостей относительно
друг друга.
55
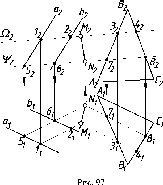
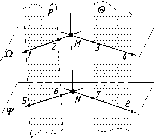
Алгоритм
решения задачи проиллюстрирован на
рис. 96. Здесь Р, 0 - заданные плоскости
общего положения, Q,
¥
- вспомогательные секущие плоскости;
12, 34 - линии пересечения секущей плоскости
Q
с
заданными плоскостями; М
- первая искомая точка линии пересечения,
56, 78 - линии пересечения секущей плоскости
¥ с заданными плоскостями; N
-
вторая искомая точка линии пересечения;
MN
-
искомая линия пересечения.
Следует
напомнить, что в качестве вспомогательных
удобнее использовать секущие
плоскости частного положения. Для
построения линии пересечения, как
правило, достаточно двух секущих
плоскостей (при анализе взаимного
положения плоскостей вспомогательных
секущих плоскостей может быть больше
двух).
Приведенный
алгоритм решения задачи в пространстве
справедлив и при выполнении построения
на эпюре.
Пример
построения на эпюре задачи нахождения
линии пересечения двух плоскостей
общего положения приведен на рис. 97.
Заданы
плоскости общего положения Р (□ ABC)
и
0 (а //
в).
Для решения задачи выбираются две
секущие фронтально-проецирующие
плоскости Q
(Q2)
и
¥ (¥2),
пересекающие каждую из заданных
плоскостей.
При
пересечении плоскостей 0 и Р плоскостью
Q
(Q2)
получаются
линии пересечения с проекциями 1222,
1121,
и 3242,
3141.
Эти прямые, расположенные в секущей
плоскости Q,
в
своем взаимном пересечении определяют
горизонтальную проекцию первой искомой
точки М.
Вторая
секущая плоскость ¥ (¥2)
при пересечениями с заданными плоскостями
0 и Р дает прямые с проекциями 5262,
5161,
7282,
7181.
Эти прямые, расположенные в плоскости
¥, в своем пересечении определяют
горизонтальную проекцию второй точки
N
искомой
линии пересечения.
Фронтальные
проекции точек М
и N
находятся
на следах соответствующих секущих
плоскостей. Таким образом определяются
проекции M1N1
и
M2N2
искомой
линии пересечения плоскостей 0 (DABC)
и
Р (а || в).
В
рассмотренном построении были взяты
в качестве вспомогательных две
фронтально-проецирующие плоскости.
Результат построений не изменится,
если будут взяты иные секущие плоскости
частного положения.
При
выполнении построений рекомендуется
использовать особенности задания
плоскостей и проводить вспомогательные
секущие плоскости в соответствии с
этим. Например, иногда удобно проводить
вспомогательные секущие плоскости
через прямые, которыми задана одна из
плоскостей. В этом случае построения
сводятся к двум последовательным
решениям задачи на пересечение
прямой с плоскостью.
На
рис. 98 показан вариант введения секущих
плоскостей для случая, когда проекции
заданных плоскостей накладываются.
Заданы
две плоскости общего положения Р (DABC)
и
0 (ED
@
FD).
Фронтально-проецирующая
секущая плоскость Q
(Q2)
проведена
через
56
прямую
ED
плоскости
©. Секущая плоскость Q
(Q2)
пересекает
плоскость Р (□ABC)
по
линии 12, а плоскость © по заданной прямой
ED.
На
горизонтальной плоскости проекций
определится проекция первой точки К
искомой линии пересечения. В то же
время точку К
можно рассматривать как точку встречи
прямой ED
с
плоскостью ABC.
Для
определения второй точки искомой
линии пересечения плоскостей можно
провести секущую плоскость через любую
из сторон треугольника или через прямую
FD.
Полное
решение аналогичной задачи приведено
ниже.
остроение
линии пересечения для случая, когда
плоскости задан следами, приведено на
рис. 99. Заданы следами плоскости S
(S1,
S2)
и
© (©1,
©2).
Здесь роль секущих плоскостей выполняют
сами плоскости проекций. Точки пересечения
одноименных следов плоскостей являются
следами линии пересечения этих
плоскостей. Поэтому сначала определяются
проекция точки N2
в
пересечении фронтальных следов S2
и
©2
и проекция точки N1
в
пересечении горизонтальных следов S1
и
©1.
Потом строятся недостающие проекции
М2
и N1
и
проекции искомой линии пересечения
MN.
Таким
образом, если плоскости задают следами,
то линия пересечения данных плоскостей
проходит через точки пересечения
одноименных следов плоскостей.
57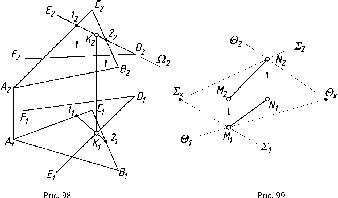
Анализ
взаимного положения прямой и плоскости,
двух плоскостей
Способ
вспомогательных секущих плоскостей
удобно использовать для анализа
взаимного положения прямой и плоскости,
двух плоскостей.
Для
прямой и плоскости возможны три варианта
их взаимного расположения: прямая
пересекает плоскость, параллельна или
принадлежит ей.
Анализ
сводится к решению задачи на пересечение
прямой с плоскостью общего положения.
Взаимное расположение прямой и линии
пересечения секущей плоскости с
заданной может быть следующим:
прямая
l
совпадает
с прямой т
т.е. данная прямая l
будет
принадлежать плоскости S
(AB @
CD)
(рис.
100 а);
прямая
l
параллельна
прямой т,
т.е. данная прямая l
параллельна
плоскости S
(AB @
CD)
(рис.100
б);
прямая
l
пересекает
прямую m,
значит,
данная прямая l
пересекает
плоскость S
(см.
рис. 94).
а)
б)
Рис.
100
58
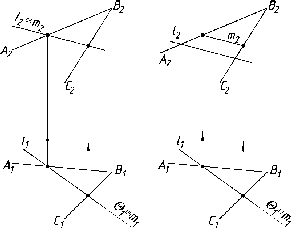
Анализ
задачи о взаимном расположении двух
плоскостей состоит в том, чтобы выяснить,
пересекаются или параллельны между
собой данные плоскости. Анализ проводится
при решении задачи на пересечение двух
плоскостей общего положения. При этом
в ходе решения задачи расположение
линий пересечения вспомогательной
секущей плоскости с каждой из заданных
может оказаться следующим:
линии
пересечения, получаемые от одной
секущей плоскости, будут параллельны:
12 || 34, а 56 || 37. В этом случае данные
плоскости параллельны между собой
(рис. 101);
линии
пересечения, получаемые от каждой
секущей плоскости, будут соответственно
пересекаться: 12 @ 34, а 56 @ 78, следовательно,
заданные плоскости Р и 0 пересекаются
между собой (см. рис. 97).
Наряду
с рассмотренным выше способом анализ
задач о взаимном пересечении прямой и
плоскости, двух плоскостей иногда проще
провести, используя способы преобразования
эпюра, которые будут рассмотрены далее.
Рис.
101
59
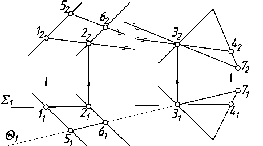
а) |
|
б) |
|
Рис. 103 |
|
60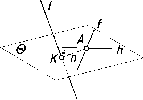
Для
построения основания перпендикуляра
точки К, как точки пересечения прямой
1
и плоскости 0,
через прямую вводится вспомогательная
фронтально-проецирующая плоскость Т
(на рис. 103 б она задана следом Т2
A
l2).
Плоскости
Т и 0 пересекаются по линии MN
с
проекциями M1N1
и
M2N2.
На
пересечении построенной линии MN
и
заданной l
определяется
точка К(K\,
К2).
Прямая
АК
- искомый перпендикуляр к прямой 1. Далее
определяется натуральная величина
отрезка АК
(А0К2)
способом прямоугольного треугольника.
Задача
1а. Определить расстояние от точки до
прямой частного положения.
а) б)
Рис.
104
Если
заданная прямая занимает частное
положение, то алгоритм решения задачи
значительно упрощается (рис. 104 а). Здесь
опустить перпендикуляр из т. А
на прямую (1 a
h) можно
сразу, без введения дополнительной
плоскости, так как в этом случае прямой
угол (h
ЛАК)
спроециру- ется на плоскость П1
в натуральную величину.
На
рис. 104 б показано решение задачи на
эпюре. Сначала строится горизонтальная
проекция прямой АК
(А1К1
± ^),затем с помощью линии связи фронтальная
проекция А2К2.
Способом прямоугольного треугольника
определяем натуральную величину
перпендикуляра (искомого расстояния)
- А1К0.
61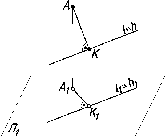
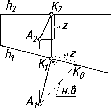
Задача
2. Через скрещивающиеся прямые провести
параллельные плоскости (рис. 105).
Пусть
заданы две скрещивающиеся прямые AB
и
CD.
Через
эти прямые можно провести только
одну пару параллельных плоскостей
(плоскостей параллелизма). Используя
признак параллельности, такие плоскости
следует определить парой пересекающихся
прямых, взаимно параллельных между
собой. Таким образом, для построения
искомых плоскостей необходимо
выполнить следующие построения.
Через
произвольную точку K,
выбранную
на прямой AB,
проводим
прямую, параллельную прямой CD
-
CD
с
проекциями C1D1
||
C1D1
и
Прямые
AB
и
CD
определяют
первую искомую плоскость S
(AB
@
CD).
Аналогично
через произвольную точку K
прямой
CD
проведем
линию параллельную прямой AB
(на
эпюре A'B'
||
A1B1
и
A'2B'2
|| A2B2).
Пересекающиеся
прямые A
B и
CD
определяют
вторую искомую плоскость S'
(A'B' @
CD),
параллельную
плоскости S
(AB
@
CD).
C
2D
2
|| C2D2.
Рис.
105
62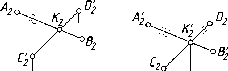
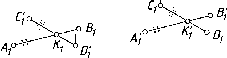
Задача
3.
Определить расстояние от точки до
плоскости общего положения (рис.
106).
Кратчайшим
расстоянием от точки до плоскости
является перпендикуляр, опущенный
из заданной точки на плоскость. Для
нахождения этого расстояния необходимо
последовательно выполнить следующие
три этапа построения:
задать
направление прямой, перпендикулярной
к заданной плоскости;
определить
точку пересечения этой прямой с
плоскостью (основание перпендикуляра);
найти
натуральную величину перпендикуляра.
В
соответствии с признаком перпендикулярности
прямой и плоскости горизонтальная
проекция перпендикулярна горизонтальной
проекции горизонтали плоскости, а
фронтальная проекция перпендикулярна
фронтальной проекции фронтали этой
плоскости.
Поэтому
для выполнения первого этапа построений
проводим в плоскости S
(□
ABC)
горизонталь
h
и
фронталь f.
Затем
через точку М
проводим прямую n,
перпендикулярную
горизонтали и фронтали плоскости, т.е.
выполняем условие: n1
L h1
□
S,
n2
L f2
□ S.
На
втором этапе решения задачи определяем
основание перпендикуляра на плоскости
-
точку
К, как точку пересечения прямой n
с
плоскостью S.
Для
этого используем способ вспомогательных
секущих плоскостей. В качестве секущей
выбрана плоскость 0
(01),
которая является горизон- тально-проецирующей
и проходит через прямую n.
На
линии 12 пересечения секущей плоскости
0 с заданной S
определится
общая точка с прямой n,
которая
и будет являться основанием перпендикуляра
на заданной плоскости - точка К (на
эпюре: 1222
@ n2
=
K2
®
K1
е
0 (01)
и n1).
По
конкурирующим точкам 4, 5, и 2, 3 определяется
видимость перпендикуляра относительно
плоскости S.
Перпендикуляр
MK
есть
прямая общего положения. Его натуральную
величину найдем способом прямоугольного
треугольника (на эпюре M0K1).
63
Рис.
106
64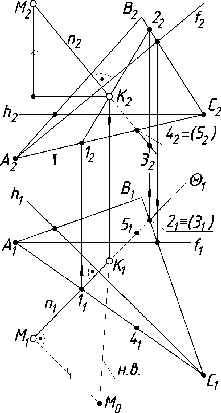
Задача
4. Построить линию пересечения двух
плоскостей общего положения (рис. 107).
Для
определения линии пересечения плоскостей
используется способ вспомогательных
секущих плоскостей. Для решения задачи
достаточно двух вспомогательных
плоскостей. Первая секущая плоскость
Q
(Qi) является
горизонтально-проецирующей и проходит
через сторону FD
треугольника
EFD.
Эта
плоскость пересекает □ ABC
по
прямой 12, которая имеет общую точку L
со
стороной FD.
Точка
L
будет
первой искомой точкой линии пересечения
(на эпюре 1222
@ F2D2
=
L2
®
L1).
Вторая
вспомогательная горизонтально-проецирующая
секущая плоскость Т (Т1)
проходит через сторону ED
треугольника
EFD.
Она
пересекает этот треугольник по
стороне ED,
а
другой (□ ABC)
-
по прямой 34. На фронтальной плоскости
проекций строится фронтальная проекция
второй искомой точки пересечения
К2
как точка пересечения прямых 3242
и E2D2.
Прямая
KL-
искомая линия двух плоскостей 0 (□ EFD)
и
S
(□
ABC).
Видимость
плоскостей определяется с использованием
двух пар конкурирующих точек (1, 5 и
6,
7).
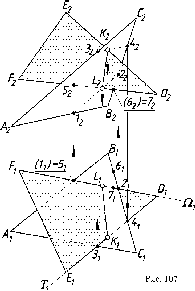
Задача
5. На скрещивающихся прямых построить
точки, находящиеся на кратчайшем
расстоянии друг от друга.
Кратчайшим
расстоянием между скрещивающимися
прямыми является перпендикуляр к
ним, основания которого (точки M
и
N)
расположены
на заданных прямых а
и b
(рис.
108 а). Если одну из заданных прямых (b)
заключить
в плоскость S,
параллельную
другой прямой а
(параллельность плоскости S
прямой
а
определена на рисунке вспомогательной
прямой ВС, лежащей в плоскости S
и
параллельной прямой а), то расстояние
между плоскостью и прямой будет величиной
постоянной. Отсюда перпендикуляр
р, опущенный из любой точки прямой а
к плоскости S,
определит
искомое расстояние между заданными
скрещивающимися прямыми. Перпендикуляр
р
и прямая а
образуют плоскость 0,
перпендикулярную построенной
плоскости S.
Там,
где плоскость 0 пересечет прямую b,
определится
первая искомая точка N.
Перпендикуляр
р'
|| р, восстановленный из точки N
до
пересечения с прямой а,
даст вторую искомую точку M.
На
рис. 108 б приведено решение задачи на
эпюре. Через прямую b
проведена
пересекающаяся с ней прямая ВС
параллельно данной прямой а,
образуя таким образом плоскость S
(b1
@
B1C1
=
B1;
b2
@
B2C2
=
B2).
Из
произвольной точки А
на заданной прямой а
опущен перпендикуляр р
к плоскости S:
р1
± h1
□
S,
р2
± f2
□
S.
Прямая
а
и перпендикуляр р
образуют плоскость 0 (а @ р), перпендикулярную
плоскости S
(b @
BC).
Для
определения точки встречи прямой b
с
плоскостью 0
введена вспомогательная секущая
плоскость Q
(^2),
которая пересекает плоскость 0 по
прямой 12. Пересечение прямых b
и
12 даст искомую точку N
-
основание перпендикуляра на прямой b.
Восстановив
из точки N
искомый
перпендикуляр р'
параллельно построенному р,
до пересечения а
, получают вторую точку M
-
основание перпендикуляра на прямой а.
Таким образом, MN-
кратчайшее расстояние между
скрещивающимися прямыми а
и b.
66
Рис.
108 а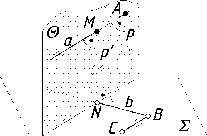
Рис.
108 б
67
Задача
6.
В заданной плоскости построить г.м.т.,
равноудаленных от двух точек пространства.
Г
еометрическим местом точек, равноудаленных
от заданных точек М
и
N
(рис.
109 а), является, как известно, плоскость
0,
проходящая через середину отрезка
MN
(точка
D)
и
перпендикулярная ему. Искомое же г.м.
точек, по условию задачи расположенных
в заданной плоскости S,
будет
находиться на линии пересечения KL
этой
плоскости S
и
построенной плоскости 0.
На
эпюре (рис. 109 б) через середину отрезка
MN
и
перпендикулярно ему проведена плоскость
0, заданная фронталью f
и
горизонталью h.
Линия
пересечения KL
плоскости
0 (h
@
f)
и
заданная плоскость S
(□
ABC)
определена
способом вспомогательных секущих
плоскостей. Первая секущая плоскость
Q
(Q1)
||
П2,
проведенная через фронталь f
плоскости
0, пересекает плоскость ПАВС по линии
n.
На
фронтальной плоскости проекций при
пересечении фронтальной проекции n2
и
фронтальной проекции f2
получается
проекция K2
первой
искомой точки линии пересечения K.
Вторая
секущая плоскость Q'
(Q'2)
||
П1,
проведенная через горизонталь
плоскости 0, пересекает плоскость
треугольника ABC
по
линии т. На горизонтальной плоскости
проекций при пересечении соответствующих
проекций горизонтали и линии т
находится проекция L1
второй
искомой линии пересечения L.
Соединив
полученные одноименные проекции точек
K
и
L,
определяем
проекции линии KL
-
искомого г.м.т.
Рис.
109 а
68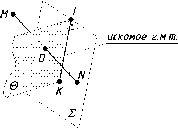
Q\
Q
Рис.
109
б
69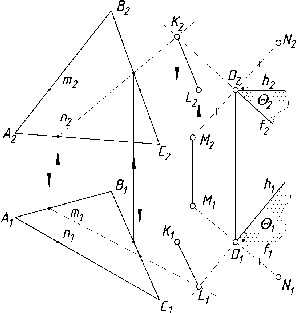
Изложенный
в предыдущих
разделах материал позволяет сделать
вывод,
что решение задач позиционного и,
главным образом, метрического
характера
значительно облегчается, если г.о.
(прямые или плоскости) за-
нимают
частные положения относительно
плоскостей проекций. Перевода
г.о.
из общего в частное положение можно
достичь использованием спосо-
бов
преобразования чертежа. При ортогональном
проецировании такой пе-
ревод может
осуществляться двумя путями:
изменением
положения плоскостей проекций
относительно г.о., ко-
торый остается
неподвижным;
перемещением
г.о. относительно плоскостей проекций,
при этом
последние остаются
неподвижными.
Первый
путь составляет теоретическую базу
способа перемены
плоскостей проекций,
второй лежит в основе способов
плоскопараллель-
ного перемещения
и вращения.
Сущность
способа перемены (замены) плоскостей
проекций заклю-
чается в том, что
одну из плоскостей проекций ортогональной
системы
(П1
П2)
заменяют на новую (П4),
которая в совокупности с оставшейся
(не-
заменяемой) плоскостью образует
другую ортогональную систему плоско-
стей
проекций. При этом новую плоскость
вводят так, чтобы относительно
нее
проецируемый г.о. занял частное положение.
Рассмотрим
механизм
введения дополнительной
плоскости
проекций (рис.110).
Плоскость
П2
заменяем на но-
вую плоскость П4,
расположен-
ную к П2
под углом, не равным
90° (в данном
случае этот угол
выбран произвольно).
При этом
П4
будет перпендикулярна го-
ризонтальной
плоскости проек-
ций П1
и пересекать ее по оси
х1
Ни o1.
Точка
ортогонально проеци-
руется
на П4,
образуя новую Рис. 110 . _
проекцию
- :4.
Так™ образ™,
будем
иметь две системы плоскостей проекций
- старую П1П2
и новую П1П4
с общей плоскостью П1.
Из рис. 110 видно, что расположение т. :
относительно общей плоскости проекций
не изменяется, т.е. координата z
точки
: остается постоянной в обеих системах.
70Преобразование чертежа
Способ перемены плоскостей проекций
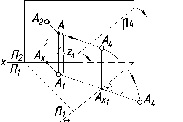
Эти
же рассуждения сохраняются и при
построении новой проекции точки на
эпюре, полученном после совмещения
плоскостей П1
и П4
с плоскостью П2.
Вариант совмещения П1
с П2
уже рассматривался выше. Совмещение
же П4
с П2
осуществляется вращением П4
вокруг оси х1
в любом направлении (выбор направления
никак не влияет на результаты
преобразования). На рис. 111 представлены
эпюры точки А, полученные перемещением
плоскости П4
в разных направлениях.
а) б)
Рис.
111
Анализируя
рис. 110, можно сделать вывод, что в нашем
примере равенство аппликат у новой
(А4)
и старой (А2)
фронтальной проекции точки А, а также
использование в обеих системах
прямоугольного проецирования делают
построение новой проекции на эпюре
чрезвычайно простым. Оно состоит в том
(см. рис. 111),
что через старую горизонтальную проекцию
точки (:1)
проводят линию проекционной связи,
перпендикулярную новой оси (х1),
и откладывают на ней, от точки пересечения
с осью, отрезок А4
Ах
1,
равный исходной координате zA
(Л2
Ах).
При
замене горизонтальной плоскости
проекций на новую (рис.112 а) для двух
систем остается постоянной плоскость
П2
и, следовательно, координата у.
Это постоянство координаты у
лежит в основе построения эпюра (рис.
112
б).
При
решении задач приходится менять либо
одну из заданных плоскостей проекций,
либо последовательно обе, если заменой
одной плоскости не удается получить
необходимого расположения проецируемого
г.о. по отношению к новой плоскости
проекций. Механизм такой двойной замены
плоскостей проекций показан на примере
(рис. 113 а) построения проекций точки.
71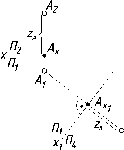

Рис.
112
Здесь
сначала плоскость проекций П2
заменяют плоскостью проекций П4,
а затем плоскость проекций П1
- плоскостью П5,
т.е. последовательно переходят от
системы плоскостей проекций П1П2
к системе П1П4,
а затем от системы плоскостей П1П4
к системе П4П5.
На
эпюре (рис. 113 б) для построения новых
проекций А4
и А5
используют неизменность отрезка
А2АХ
(координаты z)
при
переходе от системы П1П2
к системе П1П4
и отрезка А1АХ1
при переходе от системы П1П4
к системе П4П5.
Следует
отметить, что при введении новой
плоскости проекций (а следовательно,
и новой оси на эпюре) удаление последней
от заданного г.о. (проекции г.о.) выбирается
произвольно, так как не влияет на
конечный результат построений.
Важную роль играет лить
расположение новой плоскости (оси)
относительно г.о. (проекции г.о.).
а) б)
Рис.
113
72
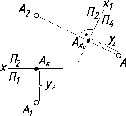
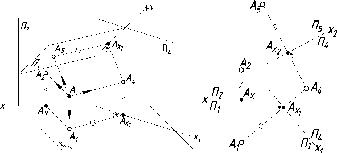
Преобразование
прямой общего положения в линию уровня
и
в проецирующую прямую
Первое
преобразование (замена).
Переведем прямую АВ
общего положения сначала в положение
уровня. Для этого заменим одну из
плоскостей проекций системы П1П2,
например П2,
на новую плоскость П4,
которая будет параллельна АВ
и, в свою очередь, перпендикулярна
старой плоскости П1.
На П4
прямая проецируется, в этом случае, в
натуральную величину (положение уровня).
Необходимые
построения на эпюре, выполняемые при
первой замене плоскости проекций (рис.
114):
проводится
ось х1
параллельно горизонтальной проекции
прямой
проводятся
линии проекционной связи из А1
и В1
перпендикулярно оси х1;
для
построения проекции А4В4
на линиях связи от новой оси х1
откладываются расстояния, равные
аппликатам точек А
и В.
Проекция
А4В4
- натуральная величина прямой АВ.
Угол
(а) между А4В4
и осью х1
- угол наклона прямой к плоскости
проекций П1
(вариант решения задачи на определение
угла наклона прямой общего положения
к П1).
(А1В1);
5
Рис.
114
Рис.
115
73
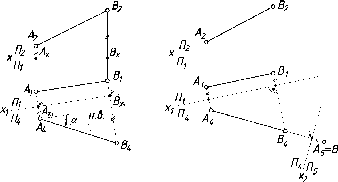
Второе
преобразование (замена).
Еще одну замену плоскости проекции
проводим для перевода прямой АВ
в проецирующее положение. При этом за
«старую» систему плоскостей проекций
принимаем уже не П1П2,
а П1П4,
в которой прямая АВ является линией
уровня.
Заменим
старую плоскость проекций П1
на новую плоскость проекций П5
так, чтобы П5
была перпендикулярна прямой АВ и
плоскости проекций П4.
На эпюре (рис. 115) выполняются построения:
проводится
ось х2
перпендикулярно А4В4
и линия проекционной связи как
продолжение А4В4;
откладывается
на ней (от оси х2)
расстояние, равное величине удаления
проекций А1
и В1
от оси o1.
На
чертеже эти отрезки обозначены «□».
В
результате получаем проекцию - точку
(А5
° В5)
прямой, которая заняла проецирующее
положение относительно плоскости
проекций П5.
Преобразование
плоскости общего положения в проецирующую
плоскость и в плоскость уровня
Первое
преобразование (замена).
При выполнении этого этапа до-
полнительную
плоскость проекций следует ввести
перпендикулярно одной
из линий
уровня плоскости - горизонтали или
фронтали. Именно в этом
случае
заданная плоскость займет проецирующее
положение относительно
новой
плоскости проекций.
На
рис. 116 показаны построения
первого
этапа преобразования, выпол-
ненные
на эпюре в случае замены
фронтальной
плоскости проекций:
строятся
проекции h2,
h1
гори-
зонтали
h
плоскости
S
(ПАВ
K);
проводится
ось проекций х1
перпендикулярно
h1
-
горизонтальной
проекции горизонтали;
проводятся
линии проекцион-
ной связи из точек
А1,
В1,
С1
перпенди-
кулярно х1;
на
линиях связи от оси х1
от-
кладываются соответствующие
отрезки
и строится проекция А4В4С4
плоскости
S
(ПАВС),
которая вырождается на П4
в
прямую линию S4.
Здесь
можно уви-
деть угол (а)
наклона плоскости S
к
П1
(вариант
решения задачи на определение угла
наклона плоскости общего положения к
горизонтальной плоскости проекций).
Рис.
116
74
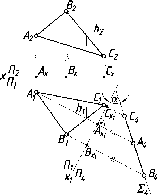
Второе
преобразование (замена)
позволяет перевести плоскость S
(□
ABC)
из
проецирующего положения в положение
плоскости уровня. Для этого дополнительную
плоскость проекций П5
вводят параллельно заданной плоскости,
образуя при этом с плоскостью П4
ещё одну ортогональную систему
плоскостей проекций П4П5.
В этой новой системе заданная
плоскость станет плоскостью уровня и
спроецируется на П5
в натуральную величину. На эпюре
(рис. 117) строятся:
ось
проекций о2
параллельно следу S4
данной
плоскости на П4;
линии
проекционной связи из A4,
B4,
С4
перпендикулярно х2;
с
использованием соответствующих
отрезков строится проекция A5B5C5
плоскости
в виде натуральной плоской фигуры
(вариант решения задачи на нахождение
н.в. плоской фигуры, занимающей
проецирующее положение).
Рис.
117
Следует
помнить: преобразовать прямую общего
положения в проецирующую прямую
(или плоскость общего положения в
плоскость уровня) одной заменой
плоскости проекций невозможно. Это
следует из того, что новая дополнительная
плоскость проекций, перпендикулярная
прямой общего положения (или параллельной
плоскости общего положения), должна
быть плоскостью общего положения, что
нарушает ортогональность плоскостей
проекций в новой системе.
75
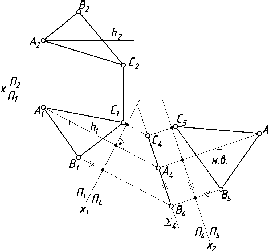
Преобразование
плоскости общего положения, заданной
следами,
в
проецирующую плоскость
В
случае задания плоскости следами (рис.
118) для перевода ее из общего положения
в проецирующее необходимо, чтобы один
из заданных следов на эпюре стал
перпендикулярен к оси х1
новой ортогональной системы П1П4.
Тогда в этой системе плоскость займет
проецирующее положение относительно
П4.
На
рис. 118 ось х1
проведена перпендикулярно следу S1.
В
этом случае для определения направления
нового следа S4
достаточно
взять произвольную точку А2
на следе S2
и
указать ее проекцию на новой плоскости
П4
в
соответствиями с правилами построения,
изложенными ранее. В новой системе П1П4
плоскость S
(S1,
S4)
займет
проецирующее положение относительно
П4.
Сущность
способа заключается в том, что все точки
геометрического образа, меняющего свое
положение в пространстве, перемещаются
в плоскостях, параллельных какой-нибудь
из плоскостей проекций (рис. 119 а, б),
траектория перемещения - произвольные
линии (l,
/,
Г....).
При
параллельном переносе ортогональная
проекция г.о. на плоскость, параллельно
которой происходит перемещение его
точек, сохраняет свои размеры и форму,
изменяя лить
положение относительно оси проекций
(рис. 120)
(справедливость этого утверждения при
необходимости может быть легко
доказана). Проекции всех точек г.о. на
другой плоскости
76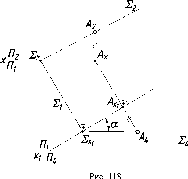
Способ плоскопараллельного перемещения
проекций
пере е а т по пря линия ,
параллельн
оси проекций и являющимся следами
плоскостей перемещения.
Произвольный
перенос одной из проекций в новое
положение позволяет избежать
наложения проекций.
а) б)
Рис.
119
Рис.
120
77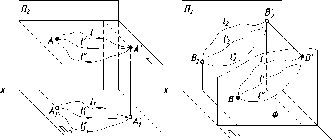
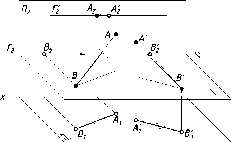
Преобразование
прямой общего положения в прямую уровня
и
в проецирующую прямую
Пусть
дана прямая АВ
общего положения. Переведем ее сначала
в положение фронтали, а затем в
горизонтально-проецирующее положение
(рис. 121).
Первое
преобразование.
Точки А
и В
перемещаются в горизонтальных
плоскостях уровня Г' и Г соответственно.
На
эпюре после переноса горизонтальная
проекция отрезка АВ
в соответствии с условиями
преобразования сохраняют свою величину:
\A'\B'\j
=
jA\B\\,
но
становится параллельной оси проекций.
Фронтальная
проекция А2
точки А
перемещается по следу плоскости
перемещения Г'2,
а проекция В2
-
по следу Г2.
Новое
положение проекций А'2
и В'2
находят на пересечении линий проекционной
связи, проходящих через А\
и В'1
со следами соответствующих плоскостей.
Проекция А'2В'2
будет натуральной величиной отрезка
АВ.
Второе
преобразование.
Фронтальную проекцию А'2В'2
перенесем в новое положение,
перпендикулярное оси х (А"2В"2
Т х).
При этом точки А' и В'
будут перемещаться во фронтальной
плоскости уровня Ф. На следе этой
плоскости (Ф1)
будет располагаться новая горизонтальная
проекция прямой - точка (А"1
° В"1).
78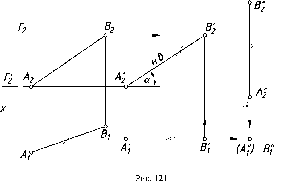
Преобразование
плоскости общего положения в проецирующую
плоскость и в плоскость уровня
Рис.
122 дает полное представление о
геометрических построениях, выполненных
в результате этих преобразований.
Последовательность этих построений
указана индексами - штрихами, поставленными
у проекций справа вверху и стрелками.
Перемещение точек плоскости S
(□
ABC)
вначале
производим в плоскостях Г, Г' ,Г",
параллельных П1
(перевод во фронтльно-проецирующее
положение), а затем в плоскостях Ф, Ф',
Ф", параллельных П2
(горизонтальное положение уровня).
При
первом перемещении проекцию A'1,
B\,
C'1
располагаем
так, чтобы проекция горизонтали плоскости
h1
стала
перпендикулярна оси х.
При
втором перемещении след S"2
сделаем
параллельным оси х.
Рис.
122
Способ
вращения состоит в том, что г.о. вращается
в пространстве вокруг выбранной оси
до требуемого положения относительно
плоскостей проекций. Точки вращаемого
предмета описывают в пространстве дуги
окружностей, лежащих в плоскостях,
перпендикулярных к оси вращения, а
центры этих окружностей располагаются
на оси вращения в точках пересечения
оси с плоскостями. В качестве осей
вращения можно применять либо проецирующие
прямые, либо линии уровня.
79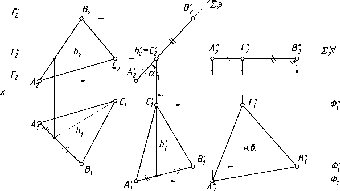
Способ вращения
Вращение
вокруг оси, перпендикулярной плоскости
проекции
Такое
вращение является частным случаем
параллельного перемещения,
рассмотренного выше. Отличие состоит
лишь в том, что за траекторию
перемещения точек в плоскостях,
параллельных плоскости проекции,
берется не произвольная линия, а
окружность.
Проследим,
как будет изменяться положение точки
: при этом способе перемещения (рис.
123).
При
вращении вокруг оси, перпендикулярной
горизонтальной плоскости проекции
Пь
точка : (см. рис. 123 а) будет перемещаться
по дуге окружности l
в
плоскости Г, параллельной Пь
Эта окружность проецируется на
плоскость П1
без искажения, а на плоскость П2
в отрезок прямой, параллельной оси x
(см.
рис. 123 б).
Вращение
точки вокруг оси, перпендикулярной
фронтальной плоскости проекций (i
Т
П2),
иллюстрирует рис. 124 а.
Здесь
точка : перемещается в новое положение
:1
по окружности, лежащей в плоскости Ф,
перпендикулярной оси вращения i
и
параллельной П2.
В этом случае вращения фронтальная
проекция точки : (Л2)
будет перемещаться по окружности с
центром на фронтальной проекции оси
вращения, а горизонтальная - по прямой
Ф1,
параллельной оси x
(рис.
124
яснив
характер пере е ения проекций точки
при вра ении ее вокруг проецирующих
прямых, можно осуществить перемещение
проекций любой геометрической фигуры
при переводе ее из заданного положения
в частное.
х
Рис.
123
б).
80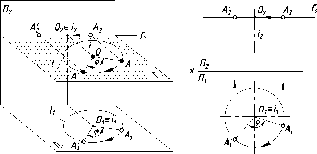
a)
б)
Рис.
124
Вращение
отрезка прямой, до положения линии
уровня и проецирующего положения
При
выполнении вращения ось можно проводить
либо в произвольном месте, либо через
одну из точек прямой. В последнем случае
решение задачи облегчается, так как
будет достаточно переместить лишь одну
точку прямой, не лежащую на оси
вращения.
Первое
вращение.
В зависимости от выбора оси вращения
(± П2
или ± П1)
прямую общего положения можно перевести
соответственно в положение фронтали
или горизонтали.
На
рис. 125 показаны построения, выполненные
при перемещении отрезка АВ
общего положения, в положение, параллельное
П2.
Ось вращения в этом случае будет
перпендикулярна Пь
Проведем ее через точку В.
На
эпюре горизонтальная проекция точки
Ai
перемещается
по дуге в положение A'i
так,
чтобы А'1В'1
была параллельна оси проекций х.
При этом фронтальная проекция А2
переместится по следу горизонтальной
плоскости уровня и займет положение
в точке пересечения следа Г2
и линии связи, восстановленной из
А'1.
Соединив А'2
и В'2,
получим фронтальную проекцию фронтали
АВ.
Второе
вращение.
Вращение фронтали (ВА') при переводе ее
в положение горизонтально-проецирующей
прямой осуществляется вокруг
фронтально-проецирующей оси /, проходящей
через точку А'.
81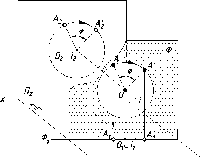
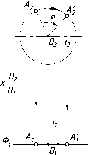
На
эпюре (см. рис. 125) фронтальная проекция
оси вращения /2
совпадет с проекциями А'2
и А"2.
Новое положение проекции В"2
получим, повернув В'2
вокруг /2
до положения отрезка А"2В"2,
перпендикулярного оси х.
Горизонтальная проекция точки В
переместится по следу Ф1
и займет новое положение В"1,
совпадающее с А\
и А"1.
Рис.
125
Вращение
плоскости общего положения до
проецирующего и положения плоскости
уровня
На
рис. 126 плоскость общего положения S
задана
ПАВ С. В том случае, когда требуется
определить истинную величину плоской
фигуры, заданной в общем положении,
необходимо осуществить два последовательных
вращения вокруг осей, перпендикулярных
вначале одной плоскости проекций,
а затем другой. Предварительно в
плоскости S
проводится
горизонталь h,
и
плоскость вращается вокруг оси i
Т
П1
до тех пор, пока горизонталь не будет
перпендикулярна плоскости П2.
Тогда плоскость общего положения
станет фронтально-проецирующей
(см.раздел. II. 4). Второе вращение
плоскости S
осуществляется
вокруг оси i
Т
П2
до положения, параллельного плоскости
П1.
В результате этого вращения фронталь-
но-проецирующая плоскость Е'(П А'В'С')
станет горизонтальной плоскостью
уровня и спроецируется на П1
в натуральную величину (□ А"1В"1С"1).
82
Рис.
126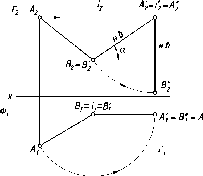
Вращение
вокруг линии уровня
Этот
способ является эффективным приемом,
упрощающим решение задач на определение
натуральной величины плоской фигуры.
Путем вращения вокруг линии уровня
можно повернуть плоскость до положения,
параллельного плоскости проекции.
При
таком повороте каждая точка г.о.
перемещается по окружности, расположенной
в плоскости, перпендикулярной оси
вращения. Центр окружности будет
находиться на оси вращения, а величина
радиуса вращения равна расстоянию
от точки до оси вращения.
Если
за ось вращения взята горизонталь (рис.
127 а), то окружность, по которой движется
точка, будет проецироваться на П1
в отрезок прямой, перпендикулярной
горизонтальной проекции оси (А). На
плоскости П2
окружность проецируется в эллипс,
построение которого можно не выполнять.
Анализируя
рис. 127 а, можно прокомментировать
построения, выполняемые на плоскости
П1,
при перемещении т. : по окружности,
плоскость которой перпендикулярна
оси вращения (h).
Здесь
сначала необходимо найти положение
центра вращения и определить натуральную
величину радиуса вращения. Проекция
01
центра вращения находится в точке
пересечения проекции оси вращения h1
с
горизонтальным следом плоско
83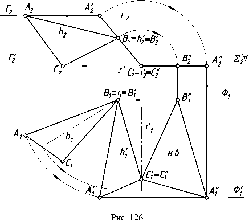
сти
S1.
Для
нахождения величины радиуса вращения
используется способ треугольника.
Строим на плоскости П1
прямоугольный треугольник, один катет
которого - проекция радиуса г
- 01А1,
а другой - разница аппликаты концов
отрезка О
А.
Гипотенуза 01А0
будет натуральной величиной г.
а)
Рис.
127
Новое,
после поворота, положение точки А (А'1)
будет находиться на следе плоскости
S1
в
месте, удаленном от точки 01
на величину натурального радиуса г
- 01A0.
Полный
эпюр точки А, перемещающейся вокруг
горизонтали h
в
положение А',
показан на рис. 127 б.
Аналогично
(рис. 128), если за ось вращения выбрана
фронталь, то траектория перемещения
точки будет проецироваться на П2
в виде отрезка прямой, перпендикулярной
фронтальной проекции фронтали. Эта
прямая есть след плоскости вращения
S2.
Центр
вращения 0
(01,02)
находится как точка пересечения S2
с
фронтальной проекцией фронтали f2.
84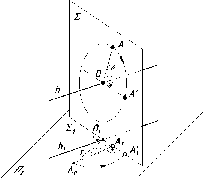
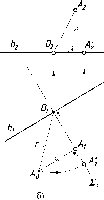
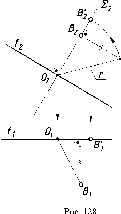
Определив
натуральнее величину радиуса вращения
ОВ,
можно найти новое положение точки
В - В'.
Пример
решения задачи на нахождение н.в. плоской
фигуры этим способом приведен в разделе
IV.4,
задача
3.
Дополнительные
сведения
Способ
вращения вокруг горизонтали или фронтали
включает в себя и вращение вокруг линии
нулевого уровня (следа плоскости). При
таком вращении плоскость общего
положения после поворота совпадает
(совмещается) с плоскостью проекций,
поэтому этот способ называют способом
совмещения. Совмещение, так же как и
вращение вокруг линии уровня, применяется
в тех случаях, когда требуется определить
истинный вид фигур, лежащих в плоскости
общего положения.
Сущность
способа совмещения проиллюстрирована
на рис. 129.
На
рис. 129 а показаны построения, выполненные
при совмещении точки А, лежащей на следе
плоскости S
(S2)
с
плоскостью П1
поворотом вокруг S1.
Последовательность
построений видна из рисунка.
Анализируя
рис. 129 а, можно видеть, что не обязательно
пользоваться построениями центра
и радиуса вращения, а нужно лишь отметить
на следе 01
плоскости, в которой происходит поворот,
отрезок, равный Ех
А2
(см. рис. 129 б). Через полученную новую
проекцию точки
А
(А'2)
проводится новый след плоскости S'2.
Рис.
129
85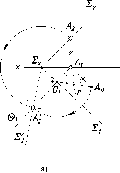
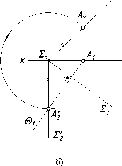
Задача
1. Определить расстояние от точки до
прямой (рис. 130).
Заданы прямые общего
положения CD
и
точка М. Задача в общем
виде решена
в разделе III.5 (задача 1). Здесь предлагается
решение задачи
способом перемены
плоскостей проекций. При решении задачи
следует
руководствоваться следующими
рассуждениями:
расстояние
от точки до прямой определяется
перпендикуляром,
опущенным из этой
точки на данную прямую;
заданная
прямая CD
занимает
общее положение, поэтому прямой
угол
между этой прямой и перпендикуляром,
проведенным к ней, проеци-
руется
на плоскости проекций с искажением.
Для
того, чтобы прямой угол проецировался
в натуральную величину,
одна сторона
его должна быть линией уровня согласно
теореме о проеци-
ровании прямого
угла. Вследствие этого прямую общего
положения CD
необходимо
преобразовать в линию уровня проецированием
на дополни-
тельную плоскость проекций
П4.Таким
образом,
первая замена плоскости про-
екций
необходима для построения пря-
мого
угла. Вторая перемена плоскости
проекций
выполняется для нахождения
н.в.
искомого расстояния. На рис. 130
первая
дополнительная плоскость П4
параллельна
прямой CD,
т.е.
ось
x1
||
C1D1,
П4
Т П1.
На новой плоскости
проекций П4
строятся н.в. CD
°
C4D4
и
точка
М4,
из которой опускается пер-
пендикуляр
к C4D4
(прямой
угол на
плоскости П4
изобразится в н.в.). Нахо-
дятся
недостающие проекции т. N
-
ос-
нования перпендикуляра.
Для
определения длины отрезка
перпендикуляра
MN
необходимо
пре-
образовать его в линию уровня.
Вво-
дится еще одна дополнительная
плос-
кость проекций П5,
которая параллель-
на MN
и
перпендикулярна П4.
На эпюре
x2
||
M4N4
и
П5
Т П4.
На
плоскости проекций П5
проек-
ция N5M5
будет
натуральной величи-
ной
искомого перпендикуляра:
|N5M5|
=
н.в. MN.
Рис.
130
86Примеры решения задач способами преобразования чертежа
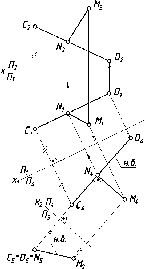
Задача
2. Определить расстояние между
параллельными прямыми (рис. 131).
Заданы
параллельные прямые общего положения
а
и b.
Расстояние
между параллельными прямыми определяется
перпендикуляром, проведенным из
произвольной точки, взятой на одной
прямой, к другой прямой. Для построения
проекций этого перпендикуляра следует
заданные параллельные прямые а
и b
проецированием
на дополнительную плоскость проекций
П4
преобразовать в прямые уровня. Для
определения н.в. перпендикуляра
выполняется вторая замена плоскости
проекций так, чтобы перпендикуляр
преобразовать в линию уровня.
На
рис. 131 плоскость П4
выбирается параллельно прямым а
и b
и
перпендикулярно П4,
т.е. х\
|| ар, х\
|| b\.
Строятся
проекции параллельных прямых а4
и b4,
которые
в новой системе плоскостей стали прямыми
уровня относительно П4
и изображаются на П4
в натуральную величину.
На
проекции прямой а4
выбирается произвольная точка N4,
из
которой проводится проекция
перпендикуляра N4M4
к
b4.
Строятся
горизонтальная и фронтальная проекции
перпендикуляра N\M\
и
M2N2.
Для
определения н.в. отрезка перпендикуляра
MN
вводится
дополнительная плоскость проекций
П5
параллельно NM
и
перпендикулярно П4.
На плоскости проекций П5
проекция отрезка перпендикуляра M5N5
равна
длине самого отрезка. Таким образом,
расстояние между параллельными прямыми
а
и b
равно
отрезку перпендикуляра MN,
натуральная
величина которого изображена на П5
и равна /M5N5|.
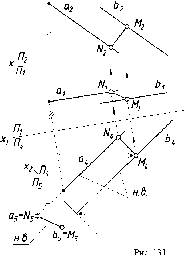
Задача
3.
Построить натуральную величину плоской
фигуры спосо
бом
вращения вокруг линии уровня (рис. 132).
Задана
S
(ПАВС)
- плос-
кость общего положения.
Определить
натуральную
величину ПАВС можно при
по-
вороте его вокруг горизонтали
данной
плоскости. Причем, ко-
гда плоскость
треугольника бу-
дет параллельна
П1,
расстояние
от каждой перемещающейся
вершины
до оси вращения, рав-
ное радиусу
вращения данной
точки, на П1
проецируется без
искажения.
При
повороте плоскости в
новое положение
вокруг гори-
зонтали h
будут
перемещаться
:
f-о
только две вершины (А и В) тре-
1
угольника, которым и задана
плоскость
S
(□
АВС).
Вершина С
остается неподвижной, так
как
Рис-
132 принадлежит оси
вращения.
Необходимые
геометрические построения на эпюре
выполняют в следующей последовательности:
строят
проекции горизонтали CD
в
данной плоскости;
находят
центры вращения точек А
и В,
для чего проводят прямые, перпендикулярные
C1D1,
по
которым будут перемещаться горизонтальные
проекции вращающихся точек. Пересечение
прямых с осью даст 01,
01
(в
данном примере центр 01
можно не использовать);
строят
проекции радиуса вращения точки А -
отрезки А101
и А2
02;
определяют
натуральную величину радиуса вращения
rA,
вращая
отрезок О
А
вокруг оси, проходящей через точку 0
и перпендикулярной П2;
отрезок
rA
откладывают
от точки 01
вдоль той прямой, по которой перемещается
горизонтальная проекция вершины А;
через
полученную точку А01
и неподвижную D1
проводят
прямую до пересечения с прямой, по
которой перемещается горизонтальная
проекция вершины В;
соединяя
найденные точки А01,
В01
друг с другом и с неподвижной вершиной
С1,
получают новую горизонтальную проекцию
треугольника, которая определяет
натуральную величину ПАВС. Фронтальная
проекция треугольника окажется
преобразованной в прямую, совпадающую
с C2D2.
88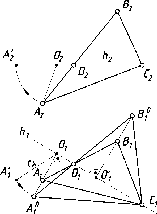
Задача
4. Определить расстояние от точки до
плоскости общего положения способом
плоскопараллельного перемещения (рис.
133).
Плоскость
общего положения необходимо преобразовать
в проецирующую плоскость. В этом
случае искомое расстояние будет
проекцией перпендикуляра, опущенного
из заданной точки на след плоскости.
Заданную
плоскость S
(□
ЛВС)
преобразуют во фронтально- проецирующую
плоскость, при этом перпендикуляр SD
к
плоскости будет фронталью (!).
При
перемещении (см. рис. 133) горизонтальная
проекция плоскости займет новое
положение, при котором ее горизонталь
станет перпендикулярна оси (h\L
x).
Сама
проекция при этом не изменяется | Л1В1С1
| @ \Л'1В'1С'1\,
сохранится также и положение точки S
относительно
точек Л', В', и С
(точка S
строится
с помощью циркуля на пересечении дуг
радиусом |В1
S11
= |B'1Sy1|
и
|C1S1|
=
|C'1Sy1|.
Положение
точки S'2
(как
и других точек Л'2,
В'2,
С'2)
определяют по линии проекционной связи
на следе Г'''2
(Г, Г', Г''), соответствующей плоскости
уровня, в которой она перемещается.
Далее
строят f2
L
Л'2В'2С'2;
! || о и находят проекции (D'2,
D1)
основания
перпендикуляра.
Выполняя
«обратное» плоскопараллельное
перемещение, строят S1D1
(применяя
засечки для нахождения D1)
и
S2D2.
89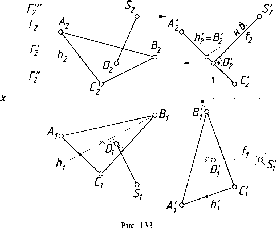
Задача
5. Построить плоскость, параллельную
плоскости общего положения и удаленную
от нее на заданное расстояние (рис.
134).
Истинную
величину расстояния между параллельными
плоскостями можно увидеть, если они
занимают проецирующее положение.
Поэтому для решения задачи преобразуем
заданную плоскость Е(ПЛВС) в горизон-
тально-проецирующую и, отмерив по
периметру от следа S4
натуральную
величину расстояния 1,
сможем провести след искомой параллельной
плоскости 0 4.
Останется перенести любую точку этой
плоскости из системы ЩП4
в систему П1П2
и через нее уже в этой системе построить
модель параллельной плоскости. На эпюре
выполняются следующие построения:
строится
проекция заданной плоскости S
(□
ЛВС)
на плоскость проекций П4.
Это прямая Л4С4В4
(S4);
от
точки Л4
(или любой другой точки) на перпендикуляре
к S4
откладывается
отрезок \A4D4\
=
1.
Через полученную точку D4
проводится
проекция 0
4
искомой плоскости (0
4
\\ S4);
строится
горизонтальная проекция отрезка AD
(AiDi\\ x4,
D4
®
D1);
находится
фронтальная проекция D2
точки
D,
преобразованием
обратным первому преобразованию;
через
D1
и
D2
проводятся
одноименные проекции параллельных
соответствующим сторонам треугольника
пересекающихся прямых
Задача
имеет два решения, т.к. искомую плоскость
можно разместить по разные стороны от
заданной плоскости. На эпюре показано
одно решение.
Рис.
134
(DE\\
AB,
DF\\
AC).
90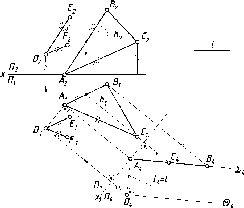
Кривуо
линию можно рассматривать как непрерывное
множество последовательных положений
точки, движущейся в пространстве, то
есть как траекторию движущейся точки.
На протяжении кривой линии не должно
быть прямолинейных участков. Кривая
линия определяется положениями
составляющих ее точек, точки кривой
определяются их координатами. Если
координаты любой точки кривой
удовлетворяют некоторому уравнению,
то такие кривые называются закономерными.
Закономерные кривые линии образуются
по определенному закону и могут быть
заданы графически и аналитически.
Аналитически
кривую линию на плоскости можно задать
уравнением
F
(x, у)
=
О
(может
оказаться, что данному уравнению F
(x, у)
= 0 не удовлетворяют координаты ни одной
действительной точки на плоскости.
Тогда условно говорят, что данные
уравнения изображаются мнимой кривой),
в пространстве - двумя уравнениями
(как линию пересечения двух поверхностей)
F
(x, у,
z)
=
0, f
(ы
у,
z)
=
0.
Существуют
также незакономерные кривые, образование
которых носит эмпирический характер.
Незакономерные кривые линии задаются
только графически на чертеже.
Одна
и та же кривая линия может быть образована
разными способами:
движением
точки в пространстве;
пересечением
кривой поверхности с плоскостью;
взаимным
пересечением двух поверхностей, из
которых хотя бы одна кривая.
Кривые
линии подразделяют на плоские
и пространственные.
У плоских кривых все точки принадлежат
плоскости, у пространственных кривых
точки не принадлежат одной плоскости.
Пространственные прямые называются
также линиями двоякой кривизны. Наиболее
известными из плоских и пространственных
кривых линий являются соответственно
окружность
и цилиндрическая винтовая линия.
Закономерные
кривые, определяемые в декартовой
системе координат
алгебраическим уравнением вида Pn
=
0,
где Pn
-
многочлен n-й
степени от одного или нескольких
переменных (n
>
1),
называются алгебраическими.
Порядком
алгебраической кривой линии
называется степень ее уравнения.
Геометрически порядок плоской
алгебраической кривой линии
характеризуется наибольшим числом
точек ее пересечения с прямой линией.
Порядок пространственной алгебраической
кривой линии определяется наибольшим
числом точек ее пересечения с плоскостью
общего положения.
91Кривые линии
К
линиям первого порядка относятся прямые
линии, рассмотренные ранее.
Линии
второго порядка - это эллипс, гипербола
и парабола.
Из
линий третьего порядка наиболее известны
Аньези локон, декартов лист,
полукубическая парабола, строфоида.
Из
линий четвертого порядка - улитка
Паскаля, конхоида Никомеда, лемниската
Бернулли.
Из
линий высших порядков - кривая Ламе,
синусоидальная спираль.
Если
закономерная кривая определяется
неалгебраическим уравнением, то она
относится к числу трансцендентных.
Среди трансцендентных кривых выделяют
графики тригонометрических функций,
показательной и логарифмической
функции, класс циклоидальных кривых,
спирали.
Локальные
свойства характеризуют кривую и
относятся к весьма малым частям ее.
Каждая из кривых линий обладает большей
или меньшей степенью искривленности.
Эта искривленность задается некоторым
числом и называется кривизной.
Кривизна
K
в
точке М - это число, характеризующее
отклонение кривой (в малой ее части,
заключающей точку М) от прямой линии.
Радиусом
кривизны г
в точке М кривой называется величина,
обратная кривизне г
=1.
Чем больше искривлена кривая вблизи
заданной точки, тем больше K
и
меньше г
в этой точке. В общем случае для любой
точки М кривизна и радиус кривизны
различны, они характеризуют кривую на
бесконечно малом участке, составляющем
окрестность точки М.
Секущей
называется прямая, пересекающая кривую
в одной, двух или более точках.
Касательная
к кривой в точке М определяется как
предельное положение секущей,
проходящей через М и соседнюю точку N
кривой,
при условии, что N
стремится
к М (рис. 135). Касательная указывает
направление движения точки.
Нормаль
для плоских кривых - это прямая,
перпендикулярная касательной в
точке касания М.
Для
пространственных кривых линий в каждой
точке М, в общем случае, определяются
три прямые и три плоскости, взаимно
пересекающиеся в М под прямыми углами
и образующие сопровождающий
трехгранник
(рис. 136). На рисунке видно, что касательная
t
к
кривой в точке М перпендикулярна
нормальной
плоскости.
Все прямые, проходящие через М и лежащие
в этой плоскости, называются нормалями
пространственной
кривой
в точке М.
92
Локальные элементы кривой
Соприкасающаяся
плоскость
- это предельное положение плоскости,
проходящей через три близкие точки
кривой М, N,
и
Р, когда N
и
Р
стремятся к М. Соприкасающаяся
плоскость содержит в себе касательную.
Главная
нормаль n
-
это линия пересечения нормальной и
соприкасающейся плоскостей (та из
нормалей, которая лежит в соприкасающейся
плоскости).
Бинормаль
b-
прямая, перпендикулярная соприкасающейся
плоскости.
Спрямляющая
плоскость
- проходит через касательную и бинормаль.
Длина
отрезка кривой (плоской
или пространственной) определяется в
общем случае приближенно путем замены
кривой линии вписанной в нее ломанной
линией с максимально большим числом
ее сторон, достаточно хорошо передающей
форму кривой.
Из
всех инвариантных свойств проецирования
для кривой линии можно выделить
следующие:
проекции
кривой в общем случае есть кривые. В
частном случае плоская кривая
проецируется в прямую, если она
принадлежит проецирующей плоскости;
если
точка лежит на кривой, то ее проекции
лежат на одноименных проекциях этой
кривой;
если
прямая касается кривой в пространстве,
то проекции этой прямой касаются
одноименных проекций кривой. Секущая
кривой проецируется как секущая
проекции кривой;
кривая,
представляющая собой проекцию кривой
некоторого порядка, сохраняет тот
же порядок или оказывается кривой
более низкого порядка.
Рис.
135
Рис.
136
свойства
проекции кривой линии
93
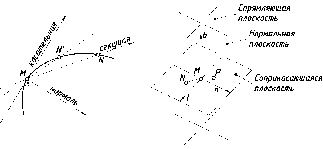
При
построении проекций плоской кривой
линии необходимо указы-
вать на их
так называемые характерные точки, к
которым относятся осо-
бые точки
кривой, а также точки, наиболее удаленные
от плоскости проек-
ций
и наиболее близкие к ним. Плоская кривая,
к каждой точке которой
можно провести касательную,
называется плавной. Однако на кривой
мо-
гут
существовать точки, в которых имеются
две касательные, общая каса-
тельная
для двух ветвей или нескольких витков
кривой. Кривая в таких
точках не
является плавной.
Пусть
касательная t
перекатывается
по
кривой 1,
при этом переменная точка касания
N
совершает
поступательное движение по ка-
сательной
(рис. 137). В каждом своем положе-
нии
переменная точка касания N
совпадает
с
произвольной точкой М, перемещающейся
по
кривой 1:
N
=
M;
N0
= M0;
N
1
= Mи
т.д.
Если
в некоторой точке N изменяется
направление
поступательного движения ее по
касательной,
то она называется особой
точкой.
Если
в некотором положении изменяется
направление поворота касательной
t,
то
она называется особой
касательной.
Если
таких изменений не происходит, то точка
N
и
касательная t
называются
обыкновенными.
Соответствующая точка М кривой также
называется обыкновенной (рис. 138 а).
(N)°
\N°M
Рис.
137
М
б)
в)
ti=t?
г)
д)
е)
Рис.
138
ж)
94Плоские кривые линии
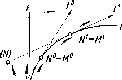

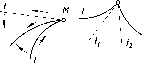
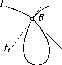
На
рис. 138 представлены некоторые особые
точки кривых:
точка
перегиба (с особой касательной) (см.
рис. 138 б);
точка
возврата первого рода или заострения
(особая точка) (см.рис.138 в);
точка
возврата второго рода, или «клюв»
(особая точка с особой касательной)
(см. рис. 138 г);
точка
излома в которой имеются две касательные
(см. рис.138 д);
узловая
точка В, в которой кривая пересекает
себя и имеет две касательные (см.
рис. 138 е);
точка
самоприкосновения С, в которой кривая
встречает самое себя, но обе
касательные совпадают (см. рис. 138 ж).
На
комплексном чертеже задаются проекции
нескольких обыкновенных и всех
особых точек кривой линии. Касательные
и нормали к кривым линиям строят или
графически, или пользуясь специальными
приборами.
На
рис. 139 показано построение касательной
к кривой линии, проходящей через
заданную вне кривой точку М. Через точку
М проводят пучок прямых, пересекающих
кривую по хордам 11, 22, 33, ... . Через
середины хорд проводят кривую ab,
которая
называется кривой
ошибок.
Эта вспомогательная кривая пересекает
данную кривую в точке С,
являющейся точкой касания. Прямая СМ
есть касательная к данной кривой линии.
Построение
нормали к кривой линии, проходящей
через заданную точку К вне кривой,
показано на рис. 140. Принимая точку К за
центр, проводят ряд окружностей,
пересекающих кривую по хордам 11, 22, 33 и
т.д. Из концов хорд проводят разносторонне
направленные перпендикуляры к ним, на
которых откладывают отрезки, равные
длинам соответствующих хорд. Концы
отрезков этих перпендикуляров намечают
кривую ошибок - линию ab,
пересекающую
данную кривую в точке С. Прямая КС задает
направление искомой нормали n
к
данной кривой.
95
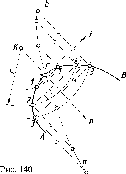
Кривые
линии называются соприкасающимися,
если в общей их точке М они имеют
общую касательную. Нормали кривых линий
в точке соприкасания лежат на одной
прямой.
Рис.
141
Соприкасание
называется внутренним,
если в точке соприкасания нормали
кривых совпадают (рис. 141 а). Если нормали
направлены в разные стороны, то
кривые линии имеют внешние
соприкасания (рис. 141 б).
Соприкасающаяся
окружность
в данной точке кривой определяет
кривизну плоской кривой в этой точке.
Соприкасающейся окружностью или кругом
кривизны кривой называют предельное
положение окружности, когда она
проходит через данную точку и две
бесконечно близкие к ней точки кривой.
Радиус этой окружности г
есть радиус кривизны, а центр 0
- центр кривизны кривой линии в данной
точке (рис. 142).
t
Геометрическое
место центров кривизны a0b0
для
всех точек данной кривой АВ есть кривая,
называемая эволютой
(рис. 143).Она является огибающей
нормалей данной кривой.
Рассматриваемую
кривую линию АВ
по отношению к своей эволюте называют
эвольвентой.
Касательные эволюты являются нормалями
эвольвенты. Через каждую точку
касательной к эволюте проходит одна и
только одна эвольвента. Всякая плоская
кривая линия есть геометрическое место
центров кривизны бесчисленного множества
эвольвент.
96
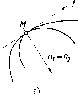
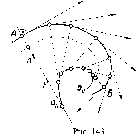
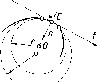
4.
И
ИХ ПРОЕКЦИИ
лгебраическу
криву лини , которая опис вается в систе
е декартовых координат уравнением
второй степени относительно текущих
координат, называют линией второго
порядка.
Общее
уравнение второй степени с двумя
переменными имеет вид:
Ах2
+
Вху + Cy
+
Dx
+
Ey
+
F
=
0.
После
приведения уравнения кривой к
каноническому виду кривые могут быть
квалифицированы следующим образом:
кривые
эллиптического типа. Это эллипс (в
частном случае окружность, одна
точка или мнимое место точек);
кривые
гиперболического типа. Это гипербола
или пара пересекающихся прямых;
кривые
линии параболического типа - парабола,
пара параллельных прямых (в частном
случае совпадающих) или мнимое место
точек.
Кривые
линии второго порядка называют кониками
или линиями конических сечений, так
как они могут быть получены в сечении
плоскостью прямого кругового конуса.
Конические сечения будут рассмотрены
далее (Раздел VII.1.).
Кривую
второго порядка однозначно определяют
заданием пяти точек общего положения:
через заданные пять точек проходит
одна и только одна кривая второго
порядка. Если хотя бы три точки лежат
на одной прямой, то получается
распадающееся коническое сечение.
Эллипс
представляет собой геометрическое
место точек, сумма расстояний от
каждой из которых до двух данных точек
(фокусов) есть величина постоянная.
Каноническое уравнение эллипса имеет
вид
22
x
y
2
2
2
—г
+ ^л- =
1,
где b
=
a
-
c
.
a2
b2
Оси
координат являются осями симметрии
эллипса (рис. 144). Точка 0
пересечения
осей симметрии называется центром
эллипса, точки пересечения эллипса
осями симметрии - вершинами эллипса.
Отрезки, соединяющие противоположные
вершины эллипса, равные 2а
и 2
b, называют
соответственно большой и малой осями
эллипса. Два фокуса эллипса - точки F1
и
F2
расположены
на расстоянии 2с друг от друга. Величину
2с называют фокусным расстоянием.
Любая точка Е плоскости принадлежит
эллипсу,
если
соблюдается условие EF1
+
EF2
=
2
a,
где 2а - большая ось эллипса.
Диаметры
эллипса - это отрезки прямых, проходят
через центр эллипса. Геометрическим
местом середин хорд, параллельных
одному из диаметров эллипса, является
диаметр, сопряженный заданному. На
рис.145 диаметры 2а1
и 2b1
является
сопряженными. Большая и малая оси
эллипса являются сопряженными взаимно
перпендикулярными диаметрами.
97
Касательные,
проведенные к эллипсу в концах какого-либо
диамет-
ра, параллельны другому
диаметру, сопряженному с первым.
Касательная
tE
к
эллипсу составляет равные углы с
фокальными радиусами-векторами
точки
касания. Нормаль nE
эллипса
в заданной точке является биссектри-
сой
угла между фокальными радиусами-векторами
этой точки (см. рис. 144).
Частным
видом эллипса является окружность.
Если фокусы F1
и
F2
=
2
a
имеем
совпада
т то из условия
EFi
+
EFi
=
a
получа-
ется
гео етрическое есто точек, равноудаленн
х от одной данной точки, т.е. окружность.
Эллипс есть кривая, родственная
окружности. На родстве двух фигур
основан ряд способов построения эллипса.
Рис.
144 Рис. 145
На
рис. 146 представлен один из способов
построения эллипса по его сопряженным
диаметрам. Этот способ используют в
случае, когда эллипс проецируется на
плоскости проекций в виде эллипсов.
Пусть
заданы проекции двух произвольно
выбранных и делящихся пополам отрезков
- А\В\
и C\D\.
Эти
отрезки можно рассматривать как
сопряженные диаметры эллипса. Один
из отрезков, например А1В1,
примем за диаметр окружности, родственной
эллипсу. Здесь диаметр окружности АВ
совпадает с диаметром А1В1
эллипса. Диаметры АВ и CD
родственной
эллипсу окружности являются взаимно
сопряженными, т.е. взаимно перпендикулярными.
Построив окружность и наметив на ней
ряд точек Е,
можно
определить соответствующий им ряд
точек Е1
эллипса.
98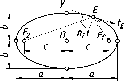
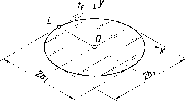
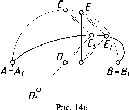
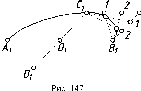
Другой
способ построения эллипса по его
сопряженным диаметрам показан на рис.
147. На полудиаметрах эллипса 01С1
и 01В1
строят параллелограмм. Стороны
параллелограмма делят соответственно
на одинаковое число равных отрезков.
Лучи, проведенные из точек С1
и В\
концов полу- диаметров через одинаково
нумерованные точки сторон параллелограмма,
пересекаются в точках эллипса.
На
рис. 148 показан способ построения эллипса
по заданным осям. Для построения точек
эллипса из центра 0
проводят две окружности, диаметрами
которых являются большая А1В1
и малая C1D1
оси
эллипса. Из центра 0
произвольно проводят луч, который
пересекает окружности в точках Е
и К.
Из этих точек проводят прямые, параллельные
соответственно осям А1В1
и C1D1
эллипса.
Точка К1
их пересечения является точкой эллипса.
Выбирая другие лучи и помечая точки на
окружностях, строят соответствующие
точки эллипса.
Рис.
148 Рис. 149
В
начертательной геометрии эллипсы чаще
всего рассматривают как проекции
окружности. При ортогональном параллельном
проецировании окружность может
проецироваться на плоскости проекций
в виде отрезка прямой, окружности
(частные случаи) или в виде эллипса
(общий случай).
Окружность
проецируется на плоскость проекций
без искажения, если ее плоскость
параллельна плоскости проекций. Пусть
окружность лежит во фронтальной
плоскости уровня, тогда ее фронтальная
проекция есть окружность, а горизонтальная
- отрезок, равный диаметру и параллельный
оси проекций х (рис. 149).
Если
окружность принадлежит проецирующей
плоскости, то одна из ее проекций
совпадает со следом плоскости и равна
диаметру окружности, а другая есть
эллипс.
99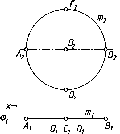
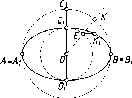
Пусть
окружность данного диаметра принадлежит
заданной горизон- тально-проецирующей
плоскости S
(S1)
(рис.
150). Горизонтальная проекция окружности
А1В1
равна диаметру и совпадает со следом
плоскости S.
Фронтальная
проекция окружности есть эллипс, большая
ось которого а
есть
проекция вертикального диаметра CD
окружности.
Большая ось эллипса является
горизонтально-проецирующей прямой и
на П2
изображается в истинную величину,
равную диаметру окружности. Малая ось
эллипса b
перпендикулярна
большой оси и параллельна оси х, она
является горизонталью. Таким образом,
фронтальная проекция горизонтального
диаметра окружности есть малая ось
эллипса.
Построение
других точек эллипса выполняют способом
хорд. Хорды параллельны вертикальному
диаметру и на П2
проецируются в натуральную величину.
Для более точного построения на чертеже
ось проекций х проводят через фронтальную
проекцию центра эллипса - точку 02.
Вводят дополнительную плоскость
проекций П4,
которая совпадает с плоскостью S
(на
чертеже новая ось х1
совпадает со следом S1).
На плоскости проекций П4
изобразится только половина окружности
с положительными координатами z,
равными
половине хорд. Величину координаты z
откладывают
от оси х по линиям связи вверх и вниз.
Получаются две точки эллипса ?2
и ?2,
симметричные
относительно малой оси. Аналогично
строят другие точки эллипса.
100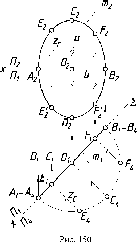
Если
окружность принадлежит плоскости
общего положения, то ортогональными
проекциями ее являются эллипсы. Большая
ось эллипса равна и параллельна тому
диаметру окружности, который параллелен
данной плоскости проекций. Малая
ось эллипса равна проекции диаметра
окружности, являющегося линией
наибольшего ската плоскости этой
окружности.
Пусть
окружность лежит в плоскости общего
положения, заданной горизонталью и
фронталью: S
(h @
f),
точка
пересечения которых принимается за
центр окружности 0
(рис. 151). Диаметр окружности 12 совпадает
с горизонталью, а диаметр 34 совпадает
с фронталью. На горизонтальной
плоскости проекций большая ось эллипса
совпадает с проекцией горизонтали
1 i2i.
Малую ось эллипса 5i6i
определяют
с помощью дополнительной плоскости
проекций П4,
перпендикулярной заданной плоскости
S.
На
П4
окружность проецируется в отрезок,
равный диаметру. В системе плоскостей
П1П4
решаем ранее рассмотренную задачу
построения эллипса как проекции
окружности, лежащей в проецирующей
плоскости. Аналогично можно построить
большую и малую оси эллипса - фронтальной
проекции окружности. Однако здесь
приведен другой способ построения
эллипса. На фронтальной плоскости
проекций большая ось эллипса совпадает
с направлением фронтали плоскости и
равна диаметру 34 окружности. Для
построения малой оси эллипса проводят
окружность с диаметром, равным большой
оси эллипса. Через точку 12
перпендикулярно большой оси строят
соответственно полухорды 12Е2
и Е2К2
эллипса и окружности. Полухорду Е2К2
вращением вокруг точки Е2
совмещают с большой осью.
Рис.
151
101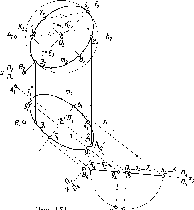
Точки
12
и К2
соединит прямой линией, параллельно
которой из точки 42
проводят
прямую до пересечения в точке 72
с направлением малой оси эллипса.
Отрезок 7202
определяет величину малой полуоси
эллипса - фронтальной проекции
окружности.
По
заданным осям можно построить другие
точки эллипса рассмотренным выше
способом (см. рис. 148).
Гипербола
-
это геометрическое место точек, для
которых абсолютная величина разности
расстояний до двух заданных фиксированных
точек (фокусов) есть величина постоянная.
Рис.
152 Рис. 153
На
рис. 152 точки F1
и
F2
являются
фокусами гиперболы. Расстояние между
ними 2с. Точка пересечения координатных
осей 0
является центром симметрии. Точки А2
и А\
- вершины гиперболы, расстояние между
ними 2а = А\А2
называют действительной осью гиперболы.
Ось симметрии CD
=
2b,
которая
не пересекает гиперболу, называют
мнимой осью.
Асимптоты
гиперболы - прямые, к которым ветви
гиперболы неограниченно приближаются
при удалении в бесконечность. Асимптоты
гиперболы направлены по диагоналям
прямоугольника со сторонами 2а
и 2b.
Каноническое
уравнение гиперболы (оси координат
совпадают с
осями
гиперболы) имеет вид
22
X
У
1 ,222
—г
- = 1, где
b
=
c
-
a
.
a2
b2
Любая
точка М плоскости принадлежит правой
ветви гиперболы, если соблюдается
условие |-MF2|
-
\MF^
=
2
a.
Точки, для которых
|MF1|
-
|MF2|
=
2a,
принадлежат левой ветви. Касательная
t
и
нормаль n
к
гиперболе
являются биссектрисами соответственно
внутреннего и внешнего углов,
образованных радиусами- векторами,
проведенными из фокусов в точку касания.
102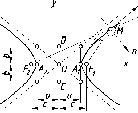
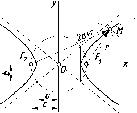
На
рис. 153 показано построение гиперболы
по точкам, если известны величины
ее полуосей а
и b.
Из
точки О, как из центра, проводят
окружность радиусом С. Окружность
пересекает ось х в точках F1
и
F2,
являющихся
фокусами гиперболы. Из фокусов, как из
центров, проводят дуги окружностей
соответственно радиусами г
и 2а +
г.
Точки их пересечения являются точками
гиперболы, так как разность расстояний
то каждой точки до фокусов равна 2а и
есть величина постоянная. Изменяя г
и повторяя построения, находят новые
точки гиперболы.
Парабола
- это геометрическое место точек
равноудаленных от фиксированной
точки (фокуса) и от заданной прямой
(директрисы).
На
рис. 154 точка F
есть
фокус параболы, а прямая АВ,
перпендикулярная оси х, - ее директриса.
Ось х совпадает с осью симметрии
параболы, точка О является вершиной
параболы. Расстояние от фокуса до
вершины параболы равно —.
Величина р называется фокальным
параметром и
2
равна
расстоянию от фокуса до директрисы или
половине хорды, проходящей через
фокус перпендикулярно оси х.
Каноническое
уравнение параболы; y2
=
2px,
гдер
= FD.
Любая
точка М плоскости принадлежит
параболе, если |MF
=
|MG|.
Касательная
t
и
нормаль n
к
параболе являются биссектрисами углов
между фокальным радиусом-вектором
точки параболы и диаметром, проходящим
через эту же точку. Под диаметром d
параболы
понимают прямую, параллельную оси
параболы. На рис. 155 показан способ
построения параболы, если известна ее
вершина - точка О и одна из точек - точка
М. Соединив вершину О с точкой М,
определяют разности координат Ах и Ay
между
этими точками. Расстояния Ах и Ay
делят
на одинаковое количество равных частей,
точки деления обозначают. Через точки
деления с одинаковыми номерами
проводят линии построения, на пересечении
которых определяют искомые точки
параболы.
103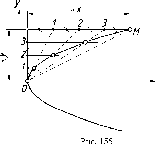

Рис.
156
Пространственн^э
кривуо линию на
чертеже задают
последовательным рядом
ее точек.
Чтобы установить особые точки
пространственной
кривой, необходимо на-
личие двух ее
проекций, в отличие от пло-
ской
кривой, для определения особых
точек
которой достаточно одной
проекции. Со-
поставление горизонтальной
и фронталь-
ной проекций на рис. 156
показывает, что
хотя на горизонтальной
проекции имеется
двойная точка, но
на самой кривой двойной
точки нет.
Так
же, как и для плоской кривой, ка-
сательная
к кривой в пространстве проеци-
руется
в касательную к проекции этой кри-
вой.
Проецирующая плоскость, проведенная
через
касательную к проекции кривой, касается
кривой в пространстве.
Но
если для плоской кривой можно было
провести только один перпендикуляр
к касательной в точке М, то для
пространственной кривой таких
перпендикуляров в точке касания
бесчисленное множество, что приводит
к понятию нормальной плоскости.
Тремя
плоскостями - спрямляющей, соприкасающейся
и нормальной (см. рис.136), образующими
трехгранник, пользуются как координатными
при рассмотрении кривой в данной ее
точке. Положение трехгранника зависит
от положения точки на кривой.
Если
касательные к пространственной кривой
линии во всех ее точках одинаково
наклонны к какой-либо плоскости, то
такие линии называются линиями
одинакового уклона.
Цилиндрические
винтовые линии
одинакового уклона широко применяются
в технике. Моделью такой линии может
служить цилиндрическая пружина.
Цилиндрическая
винтовая линия - гелиса - есть траектория
сложного движения точки, равномерно
перемещающейся по образующей и
равномерно вращающейся вместе с
этой образующей вокруг оси цилиндра.
Винтовая
линия имеет три параметра: диаметр
цилиндра, шаг и направление. Шаг -
это смещение точки вдоль образующей
за один оборот. Различают два направления
винтовой линии: правое - при движение
точки вверх против часовой стрелки и
левое - при движении точки вверх по
часовой стрелке.
104Пространственные кривые линии и их проекции
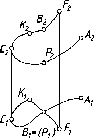
На
рис. 157 построена гелиса заданного
радиуса г, правого направления и с
шагом, равным высоте цилиндра. Для
построения проекций такой линии
длина окружности (горизонтальная
проекция цилиндра) и высота
прямоугольника (фронтальная проекция
цилиндра) делятся на 12
равных частей. Через точки деления
окружности проводят вертикальные
линии связи.
На
фронтальной плоскости проекций через
точки деления прямоугольника проводят
прямые, параллельные основанию. Точки
пересечения линий связи с соответствующей
горизонтальной прямой определяют
фронтальную проекцию цилиндрической
винтовой линии. На видимой части цилиндра
гелиса будет видимой, на невидимой -
нет. Направление винтовой линии на
чертеже определяет стрелка, поставленная
на горизонтальной проекции. Итак,
горизонтальная проекция винтовой линии
есть окружность, а фронтальная -
синусоида.
При
построении развертки цилиндрическая
поверхность развертывается в
прямоугольник со сторонами, равными
длине окружности основания и высоте
цилиндра. Винтовая линия на развертке
преобразуется в прямую - диагональ
прямоугольника, так как для каждой
точки этой прямой существует
пропорциональная зависимость между
отрезками длины окружности и высоты
цилиндра.
Рис.
157
105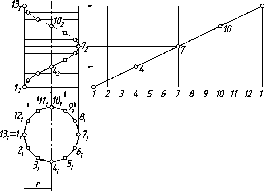
В
с^,еств^щем мире нас окружает неограниченное
количество
разнообразных поверхностей.
Некоторые могут быть математически
опи-
саны, некоторые настолько сложны,
что не поддаются математическому
описанию.
В
математике под поверхностью подразумевается
непрерывное мно-
жество точек, если
между координатами точек этого множества
может
быть установлена зависимость,
определяемая уравнением вида
F(x,y,z)=0,
где
F(x,y,z)
-
многочлен n-й
степени, или в форме какой-либо
трансцен-
дентной функции. В первом
случае поверхности называются
алгебраиче-
скими, во втором -
трансцендентными.
Если
алгебраическая поверхность описывается
уравнением n-й
сте-
пени, то поверхность считается
n-ого
порядка.
Любая
произвольно расположенная секущая
плоскость пересекает
поверхность
по кривой того же порядка (иногда
распадающейся или мни-
мой), какой
имеет сама поверхность.
Порядок
поверхности может быть определен также
числом точек ее
пересечения с
произвольной прямой, считая все точки
(действительные и
мнимые).
В
начертательной геометрии геометрические
фигуры задаются гра-
фически, поэтому
целесообразно поверхность
рассматривать как совокуп-
ность
последовательных положений линии а,
перемещающейся в про-
странстве
по определенному закону.
Закон
перемещения линии а
целесообразно
задать в виде семейства
линий m,
n, 1.
Любую из ли-
ний m,
n, 1
можно заменить описательными усло-
виями,
задающими закон перемещения линии а.
Подвижная
линия а
называется образующей,
неподвижные
линии m,
n, 1
-
направляющими
(рис.
158).
Рассмотренный
способ образования поверх-
ностей
называется кинематическим.
Поверхность
считается заданной на чертеже,
если
из множества точек пространства можно
выде-
лить те, которые принадлежат
поверхности. При
этом различают
понятия каркаса, определителя и
очерка
поверхности.
106Поверхности
Образование и задание поверхности на чертеже
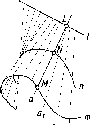
Каркас
поверхности -
множество точек или линий, определяющих
поверхность. На рис. 159 показан каркас
поверхности, состоящий из двух семейств
линий а\,
а2,
а3,...
ап
и b\,
b2,
b3,...bn.
Ф(а,
т) [А]
Рис.
159 Рис. 160
Определителем
поверхности
называется совокупность независимых
условий, однозначно задающих поверхность.
В определитель включается геометрическая
часть и алгоритмическая.
Ф
(Г)[А] - форма записи определителя, где
Ф - обозначение поверхности; (Г) -
геометрическая часть определителя -
геометрические элементы, заданные
на чертеже; [A]
-
алгоритмическая часть определителя -
показывает характер изменения формы
образующей а
и закон ее перемещения.
На
рис. 160 показана поверхность прямого
кругового цилиндра Ф (а, т)
[a
||
т, каждая точка прямой вращается вокруг
оси т]. Длинную запись алгоритмической
части иногда заменяют названием
поверхности. Пишут: поверхность вращения
Ф (а, т).
Очерком
поверхности
называется проекция проецирующей
цилиндрической поверхности, которая
огибает заданную поверхность.
Рис.
161 дает наглядное представление о том,
как получается очерк произвольной
замкнутой поверхности на горизонтальной
плоскости проекций. Здесь множество
проецирующих лучей, касательных к
поверхности, образуют горизонтально-проецирующую
поверхность. Проекцию этой поверхности
на П1
называют горизонтальным очерком
заданной поверхности.
107
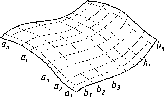
Рис.
161
Большое
многообразие поверхностей, различные
способы их образования, сложности
геометрических характеристик создают
трудности в попытках классифицировать
поверхности, объединить их в систему.
Основой
классификации поверхностей могут
служить их определители или
геометрические особенности, связанные
с кинематическим способом их
образования.
Важными
признаками формообразования поверхностей
являются:
вид
образующей и закон ее перемещения;
закон
изменения образующей;
развертываемость
куска поверхности.
На
рис. 162 приведена ориентировочная
классификация поверхностей.
Эти
поверхности относятся к группе линейчатых
развертываемых поверхностей с одной
направляющей.
Характерным
признаком торсовых поверхностей
является то, что их
прямолинейные
образующие пересекаются. При этом
пересечение может
¥
происходить
как в собственной (S),
так
и в несобственной ( S)
точках.
К
рассматриваемой группе относятся:
поверхность
с ребром возврата;
поверхность
коническая;
поверхность
цилиндрическая.
108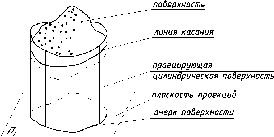
Классификация поверхностей
Обзор некоторых поверхностей Торсовые поверхности
Рис.
162
109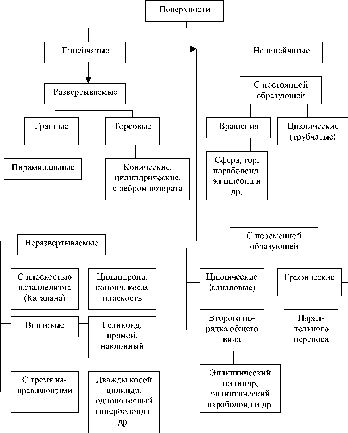
Поверхность
с ребром возврата
Поверхность
с ребром возврата в общем случае
образуется непрерывным перемещением
прямолинейной образующей (а), касающейся
пространственной кривой (m)
-
направляющей (рис. 163 а). Кривая m
называется
ребром возврата торса.
Торсовая
поверхность состоит из двух полостей,
линией раздела которых является
ребро возврата. Ребро возврата полностью
задает торс и является геометрической
частью определителя поверхности.
Алгоритмической частью служит
условие касания образующих к ребру
возврата.
Определитель
имеет вид W
(а,
m)[a
*
m].
На
эпюре Монжа любая неограниченная
торсовая поверхность задается только
проекциями ребра возврата (m1
и
m2).
При
этом каркас поверхности можно
составить из семейства прямолинейных
образующих, касательных к этому
ребру. Так, на рис. 163 б проекциями
образующей (а) являются касательные
а1
и а2
к проекциям m1
и
m2
ребра
возврата m,
проведенные
через проекции А1
и А2
случайной точки А
этого ребра.
Наиболее
широкое применение в инженерной практике
нашел частный вид торсовой поверхности
- винтовой торс, у которой ребром возврата
служит цилиндрическая винтовая линия.
Если ось винтовой линии расположить
перпендикулярно к П1,
то образованная поверхность представит
собой поверхность одинакового ската
(по отношению к П1),
т.к. все касательные к винтовой линии
пересекают плоскость П1
под одним и тем же углом. Чертеж отсека
такой поверхности показан на рис. 164.
а)
б)
Рис.
163
110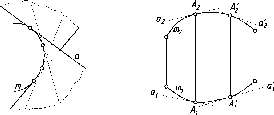
В
процессе решения многих задач приходится
задавать точки на поверхности
изучаемых предметов.
В
некоторых случаях, намечая проекции
точки на поверхности, необходимо
указывать видимость данной точки на
той или иной проекции. Такое указание
делают путем заключения в скобки
невидимой проекции точки. На данной
(как и любой торсовой) поверхности точки
могут быть построены при помощи
проходящих через них прямолинейных
образующих.
Так,
на рис. 165 показано построение фронтальной
проекции К2
точки К, лежащей на поверхности с
ребром возврата, по заданной горизонтальной
К\.
Для этого через точку К1
проведена касательная а1
к проекции т1
направляющей т. Далее через фронтальную
проекцию А2
полученной точки А на ребре возврата
т
проведена фронтальная проекция а2
касательной а, на которой расположена
точка К. Линия связи, проведенная из
К1,
определяет
искомую проекцию К2.
В
некоторых случаях недостающую проекцию
точки строят при помощи
произвольной секущей плоскости, с
расчетом, что точка должна быть в этой
плоскости.
Рис.
164
Рис.
165
111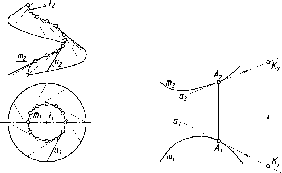
Коническая
поверхность
Коническуо
поверхность можно считать частным
случаем поверхности с ребром возврата
- при вырождении ребра возврата m
в
точку - вершину (S).
В
этом случае все образующие поверхности
будут пересекаться в собственной
точке S
и
поверхность определяется как коническая.
Для
задания конической поверхности
недостаточно иметь ребро возврата
(точку) - поверхность останется еще
неопределенной. В этом случае вводится
дополнительная линия, заведомо
принадлежащая задаваемой поверхности,
и эта линия называется направляющей
(л).
Таким
образом, коническая поверхность
образуется движением прямой (а),
проходящей через неподвижную точку
(S)
и
пересекающей кривую (л)
-
направляющую (рис. 166).
Если
направляющая л
-
замкнутая линия, то поверхность
называется замкнутой (рис. 167).
Коническая
поверхность может иметь две полости
(см. рис. 166), если образующие продолжены
за вершину.
В
случае замены кривой направляющей л
ломаной линией поверхность называются
пирамидальной (рис. 168). Поверхности с
замкнутой ломаной направляющей
называются еще многогранниками.
Аналитически
уравнение конической поверхности имеет
вид:
x
-
xA
= У
=
z
-
f
(xA)
xS
-
xA
ys
ZS
- f(xA
)’
где
х,
y,
z
- текущие
координаты точки :,
выбранной
на направляющей кривой л, имеющей
уравнение z
=
f
(x);
xs,
ys, zS
- координаты
вершины S.
Определитель
конической поверхности можно записать
следующим образом: W
(S,
a,
л) [a
CHS, a
@
л].
112
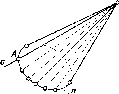
На
эпюре Монжа коническая поверхность
однозначно задается проекциями ее
образующей а
(а1,
а2),
направляющей n
(n1,
n2)
и
вершины S
(S1,
S2)
(рис.
169).
Рис.
169
Для
придания наглядности и выразительности
изображению вычерчивают очерк
поверхности и показывают наиболее
важные линии и точки на поверхности.
Рис.
170
Чтобы
построить очерк конической поверхности,
следует на каждой плоскости проекций
отметить граничные образующие,
заключающие между собой область,
внутри которой находится проекция
поверхности. Пример построения очерка
замкнутой конической поверхности (W),
заданной
определителем (рис. 170 а), показан на
рис. 170 б, в. Для построения
113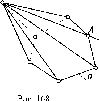
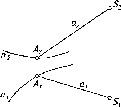

фронтального
очерка (см. рис. 170 б) на окружности п
определяют крайние точки - правая В и
левая А. Проводят образующие SA
и
SB.
Проекции
S2A2,
S2B2
и
п2
определяют фронтальный очерк поверхности.
Проекции S1A1
и
S1B1
образующих
SA.
SB
на
П1
не являются очерковыми образующими.
Для
построения горизонтального очерка
поверхности (см. рис. 170 в) проводят
касательные S1C1
и
S1D1
из
точки S1
к
окружности П1.
Чтобы определить точки касания (С1
и D1),
проводят
радиусы окружности, перпендикулярные
касательным образующим.
Для
наглядности изображаемой поверхности
невидимые элементы ее показывают
штриховой линией.
Видимую
часть поверхности на фронтальной
плоскости проекции можно определить
по горизонтальной проекции окружности
п.
А1С1В1
- обращенная
к наблюдателю часть окружности, считается
видимой на П2.
Таким образом, границей видимости
поверхности на П2
являются очерковые образующие (A2S2;
B2S2).
Видимую
часть поверхности на П1
определяют часть окружности D1A1C1
и
очерковые образующие D1S1
и
C1S1.
Конические
поверхности различают по виду нормального
сечения (нормальным сечением конической
поверхности называется сечение,
плоскость которого перпендикулярна
оси поверхности). Конус общего вида
- это коническая поверхность, у которой
нормальным сечением является
неопределенная геометрическая линия.
Выделим случаи, когда нормальное
сечение конической поверхности
представляет собой замкнутую кривую
второго порядка (конус второго порядка):
прямой
круговой конус (рис. 171 а);
эллиптический
конус (рис. 171 б);
наклонный
круговой конус (рис. 171 в) или эллиптический
конус с круговым основанием.
Рис.
171
114

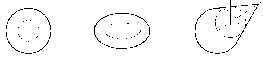
Точки
на поверхности конуса могут быть
построены при помощи
проходящих
через них образующих. На рис. 172 дан
пример построения фронтальной проекции
точки N,
принадлежащей
конической поверхности и заданной
проекцией N\,
при
условии, что эта точка видима на плоскости
Пь ход построений указан стрелками.
Пример
построения очерка прямого кругового
конуса, ось которого параллельна
плоскости П2
(но не Т П1),
приведен на рис. 173.
Фронтальный
очерк задан, это равнобедренный
треугольник A2S2B2.
Г
оризонтальный очерк состоит из части
эллипса и двух касательных к нему
прямых. Эллипс можно построить по двум
его осям: малой А1В1
и большой, равной по своей величине
диаметру окружности основания конуса.
Для определения прямых S1D1
и
S1D1,
касательных
к эллипсу, используется произвольная
сфера, вписанная в конус.
Построение
начинают с отыскания точек К2
и К'2
- фронтальных проекций случайных точек
искомых касательных. Эти точки получаются
при пересечении фронтальных проекций
окружности касания конуса и сферы и
экватора вписанной сферы. Далее находят
проекции точек К1
и К'1
на
горизонтальной проекции экватора.
Соединяют полученные точки К1
и К'1
с точкой S1.
На
этих прямых определяют и точки D
и
D',
горизонтальные
проекции которых (D1
и
D'1)
есть
точки касания прямых с эллипсом.
К2°(К'2)
Рис.
172
Рис.
173
115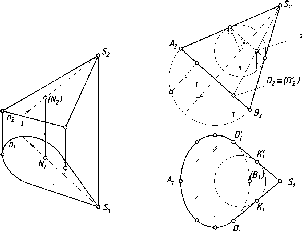
Цилиндрическая
поверхность
Цилиндрические
поверхность можно считать производимой
из поверхности с ребром возврата
при условии, что ребро возврата
представляет собой бесконечно удаленную
точку. Тогда все образующие цилиндрической
поверхности будут параллельны
(пересекаться в несобственной точке).
Для
того чтобы цилиндрическая поверхность
была определена в пространстве,
необходимо задать дополнительную
линию, принадлежащую этой поверхности;
эта линия будет называться направляющей
поверхности.
Таким
образом, цилиндрическую поверхность
можно представить как поверхность,
образованную движением прямой (а),
параллельной самой себе (или
направлению 1)
и пересекающей кривую (п)
-
направляющую (рис. 174).
Если
направляющая (п)
-
замкнутая линия, то поверхность
называется замкнутой. В случае замены
кривой направляющей (п)
ломаной линией поверхность называется
призматической (рис. 175).
Аналитическое
уравнение цилиндрической поверхности
с направляющей кривой п,
имеющей уравнение z
=
f
(x)
в
координатной плоскости x0z,
и
прямолинейной образующей а
в виде вектора {m',
п',
р'}
имеет вид:
x
-
хл
=
У
= z
-
f
(хл)
/
/ / ’ m
п р
где
х,
y,
z -
текущие координаты точек поверхности;
величина хд - параметр.
Исходя
из принципа образования поверхности,
определитель цилиндрической
поверхности можно записать следующим
образом:
Ф
(п,
1, a)
[a
Пи,
a
//
1].
116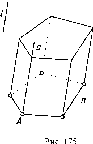
На
эпюре Монжа цилиндриче-
ская
поверхность однозначно задает-
ся
проекциями определителя: на-
правляющей
п
(п1,
п2),
образующей
а
(«1,
а2),
направлением переноса об-
разующей
1
(l1,12)
(рис. 176).
Для
наглядности изображения
цилиндрической
поверхности на
чертеже обычно строят
очерки за-
данной поверхности.
Рассмотрим
пример построения очерка
цилинд-
рической поверхности, заданной
оп-
ределителем (рис. 177 а).
Для
построения фронтального очерка
поверхности (рис. 177 б) проводят
крайние образующие АА' и ВВ',
которые на П2
являются очерковыми образующими и
служат границей видимости поверхности.
Видимость проверяют по горизонтальной
проекции окружности А1С1В1
(видимость определяют после построения
горизонтального очерка). Образующие
АА', СС', ВВ' поверхности на П2
видны.
(D'2)
Рис.
176
а)
Рис.
177
б)
ля
построения горизонтального очерка
проводят две крайние на 1
образующие
СС' и DD.
Точки
касания С1
и D1
определяют,
проводя радиусы окружности,
перпендикулярные касательным. Образующие
СС' и DD
являются
очерковыми на П1
и служат границей видимости поверхности,
а
117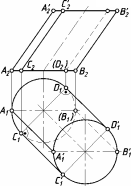
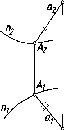
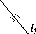
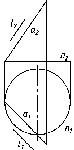
на
П2
- это промежуточные образующие. Видимую
часть поверхности на П1
можно определить по фронтальным
проекциям точек A
и
В. При взгляде сверху А2
не закрыта, а В2
закрыта частью поверхности. Соответственно
на П1
проекция A1
-
видимая, а В1
- невидимая.
Следовательно,
часть окружности C1A1D1
на
П1
считается видимой и вместе с ней видима
часть поверхности, образованная
образующими, пересекающими эту часть
окружности. Часть окружности C1B1D1
на
П1
не видна.
Цилиндрические
поверхности, как и конические, различают
по виду нормального сечения (нормальным
сечением цилиндрической поверхности
называют сечение, плоскость которого
перпендикулярна образующим поверхности).
Если нормальным сечением является
неопределенная геометрическая
линия, то это цилиндр общего вида.
Выделим
случаи, когда нормальное сечение
цилиндрической поверхности
представляет собой кривую второго
порядка. По виду полученной кривой
цилиндр может быть эллиптическим (в
частном случае круговым), параболическим,
гиперболическим. Данные цилиндрические
поверхности относятся к числу
поверхностей второго порядка. На рис.
178 показан эллиптический цилиндр,
образующие которого перпендикулярны
горизонтальной плоскости проекций.
Рис.
179
а
цилиндрической поверхности точки
строят при по о и проходящих через
них прямолинейных образующих. Так, на
рис. 179 показано построение горизонтальной
проекции М1
точки М, лежащей на цилиндрической
поверхности, по заданной фронтальной
М2.
Построения показаны стрелками.
118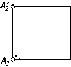
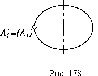
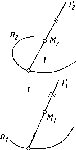
Проецирующие
поверхности
На
комплексном чертеже задачи решаются
проще, если цилиндриче-
ские и
призматические поверхности занимают
проецирующее положение,
т.е.
перпендикулярное одной из плоскостей
проекций (см. рис.178). При
таком
положении поверхности одна из проекций
образующей вырождается
в точку, а
проекция поверхности - в линию. Вырожденная
проекция по-
верхности, подобно
проецирующей плоскости, обладает
«собирательным
свойством»: проекция
любой линии, расположенной на поверхности,
на-
ходится
на вырожденной проекции поверхности.
На рис. 180 а, б показаны
случаи, когда
горизонтальная проекция поверхности
«собирает» на себя
все горизонтальные
проекции точек, расположенных на
поверхности; на
рис. 180 в, г - случаи,
когда фронтальные проекции поверхностей
«соби-
рают» на себя все фронтальные
проекции точек, расположенных на
по-
верхности. Принадлежность точек
поверхности определяется в этом
случае
принадлежностью проекций
точек вырожденной проекции поверхности.
А
(К2)
о
/г,
б)
в)
г)
Рис.
180
Эти
поверхности относятся к группе линейчатых
неразвертываемых поверхностей с двумя
направляющими. Характерным признаком
поверхностей с плоскостью параллелизма
является то, что их прямолинейные
образующие являются скрещивающимися
прямыми, так как при формировании
этих поверхностей образующие, скользящие
по двум направляющим, должны быть
параллельны некоторой заданной
плоскости. В этом случае все образующие
будут пересекаться с плоскостью
параллелизма в несобственных точках,
множество которых определяют несобственную
прямую; эту прямую следует рассматривать
как третью направляющую линейчатой
поверхности.
119
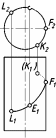

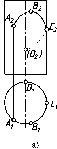
Поверхности с плоскостью параллелизма (поверхности Каталана)
Часто
поверхности с плоскостью параллелизма
называют поверхностями Каталана
(по имени бельгийского ученого-математика
Е. Каталана, исследовавшего свойства
этих поверхностей). Определитель для
группы поверхностей Каталана имеет
вид: Ф (m,
n,
S, a)
[a
@ m,
n; a
|| S], где
m,
n - направляющие
линии; а
-
образующая,
Е
- плоскость параллелизма, в качестве
которой можно выбрать любую произвольную
плоскость или одну из плоскостей
проекций. Для задания поверхности этой
группы на эпюре Монжа достаточно указать
проекции направляющих m
и
n
и
положение плоскости параллелизма. В
зависимости от формы направляющих и
их расположения в пространстве можно
получить различные поверхности этой
группы.
Рассмотрим
отдельные виды линейчатых поверхностей
с плоскостью параллелизма.
Цилиндроиды
Поверхность,
называемая цилиндроидом, образуется
в том случае, когда обе направляющие m
и
n
-
кривые линии. На рис. 181а дано наглядное
изображение цилиндроида. Для получения
проекционного чертежа, обладающего
наглядностью, обычно указывают проекции
нескольких прямолинейных образующих.
Так
как заданная плоскость параллелизма
является горизонтально- проецирующей
плоскостью S,
то
построение проекций образующих (см.
рис. 181 б) начинают с горизонтальной
плоскости проекций, на которой
горизонтальные проекции движущейся
образующей а
параллельны горизонтальному следу
S1
плоскости
параллелизма S.
Фронтальные
проекции образующих строят по двум
точкам пересечения образующей с
направляющими m
и
n.
Для
построения точки, расположенной на
поверхности, используют образующую
(или произвольную линию поверхности,
см. рис. 183).
Рис.
181
120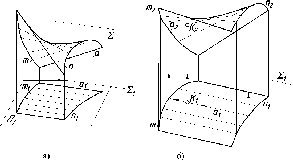
Коноиды
Отличие
поверхности коноида от цилиндроида
состоит только в том, что одна из
направляющих линий коноида - прямая.
На рис. 182 даны наглядное изображение
и эпюр Монжа коноида. Здесь m
и
n
-
направляющие, причем m
-
прямая, n
-
кривая линии; Е - горизонтально-
проецирующая плоскость, которой
параллельны все образующие коноида.
Точка К, принадлежащая поверхности
коноида, построена при помощи
проходящей через нее прямолинейной
образующей а.
Рис.
182
Косая
плоскость (гиперболический параболоид)
Косая
плоскость образуется непрерывным
перемещением прямолинейной образующей
а
по двум направляющим - скрещивающимся
прямым m
и
n
-
параллельно некоторой плоскости
параллелизма Е. Эту же поверхность
называют гиперболическим
параболоидом,
так как плоские сечения поверхности в
одном из направлений дают гиперболы,
а в другом - параболы (это положение
доказано в аналитической геометрии).
На
рис. 183 а дан пример косой плоскости с
плоскостью параллелизма Е,
перпендикулярной Пь
и направляющими прямыми m
и
n.
На
рис. 183 б приведен эпюр Монжа этой
поверхности. Для наглядности проекционного
чертежа построены проекции ряда
образующих (аналогично рис.181 б и 182 б).
Для
построения точки К
этой поверхности по заданной
горизонтальной проекции К1
использована образующая прямая а
(см. рис. 183 б). Для построения же точки
М
по заданной фронтальной ее проекции
М2
может быть использована произвольная
линия на поверхности косой плоскости,
121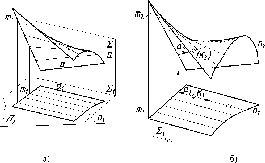
например
b,
с
расчетом, что точка М должна принадлежать
этой линии. Фронтальная проекция b2
линии
b
проходит
через М2
и пересекает ряд образующих поверхности
в некоторых точках. По горизонтальным
проекциям этих точек пересечения
строится горизонтальная проекция bi
линии
b,
а
на ней - искомая горизонтальная проекция
М1
точки М косой плоскости.
Рис.
183
Винтовые
поверхности образуются винтовым
движением прямой линии z
-
образующей (винтовое перемещение
характеризуется вращением вокруг
оси и одновременным поступательным
движением, параллельным этой оси).
Каждая точка образующей перемещается
по своей винтовой линии, причем все
винтовые линии имеют общую ось, называемую
осью винтовой поверхности (i)
(рис.
184).
При
перемещении образующей угол ее наклона
к оси и перемещение вдоль оси (называемое
шагом винтовой линии) могут меняться
или оставаться постоянными.
/77
122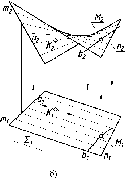
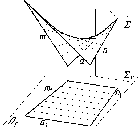
Винтовые линейчатые поверхности (геликоиды)
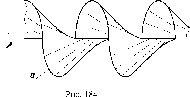
В
практике чаде всего встречаются винтовые
линейчатые поверхности с постоянным
углом наклона образующей к оси и с
постоянным шагом направляющей винтовой
линии. Эти поверхности называют еще
геликоидами (от слова «гелиса» -
цилиндрическая винтовая линия постоянного
шага).
В
зависимости от величины угла наклона
образующей к оси геликоиды бывают
прямыми, если этот угол равен 90° (рис.
185 а), и косыми (наклонными), если угол -
произвольный, отличный от 0 и 90° (рис.
185 б).
В
свою очередь прямые и косые геликоида
подразделяются на закрытые и открытые.
Признаком для такого деления служит
взаимное расположение оси геликоида
и его образующей. Если образующая и ось
пересекаются, геликоид называют
закрытым, если скрещивается - открытым.
а)
б)
Рис.
185
Рис.
186
Рис.
187
123
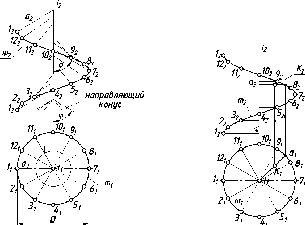
налитическое
уравнение винтовой поверхности
постоянного ага можно представить в
следующем виде:
гдер
- винтовой параметр.
Определитель
винтовой поверхности Ф(а, m)
[A], где
а
- образующая; m
-
направляющая винтовая линия; [A]
-
дополнительные данные о характере
движения образующей.
Как
неоднократно отмечалось ранее, для
получения наглядного изображения
винтовой поверхности ее задание на
эпюре Монжа проекциями геометрической
части определителя следует расширить
до задания каркасом, составленным
из последовательных положений
прямолинейных образующих.
Например,
на рис. 186 показан косой геликоид. Он
задан правой винтовой линией m
с
диаметром D,
осью
винтовой поверхности i
и
образующей а,
наклонной к оси под углом ф. Построен
один виток винтовой линии, начиная
от точки 1. Для этого окружность разделена
на 12 частей. Точка 1, перемещаясь по
винтовой линии, переходит последовательно
в положения 2, 3, ... 12. Соответствующие
образующие будут перемещаться параллельно
образующим направляющего конуса
вращения с углом ф при вершине. Построив
ряд образующих, получим дискретный
каркас отсека винтовой поверхности.
У
прямого геликоида образующие всегда
параллельны плоскости, перпендикулярной
оси поверхности (рис. 187). По своему
образованию прямой геликоид является
коноидом. Действительно, образующая -
прямая линия; она во всех положениях
параллельна некоторой плоскости (в
данном случае перпендикулярной к оси
цилиндра); образующая пересекает
две направляющие линии, кривую и прямую
(ось цилиндра). Так как кривая направляющая
представляет собой винтовую линию, то
такая поверхность называется винтовым
коноидом.
Для
построения точки К
этой поверхности по заданной фронтальной
проекции К2
использована образующая прямая а,
у которой сначала строится фронтальная
проекция а2
перпендикулярно к оси винтовой линии.
По точке пересечения (а2
@ m2)
строится
горизонтальная проекция а1
образующей и на ней точка К1.
Широкое
применение поверхностей вращения в
технике, машиностроении объясняется
распространенностью вращательного
движения и простотой обработки
(образования) деталей на станках.
Особенно распространены поверхности,
имеющие в меридиональном сечении (см.
ниже) кривые второго порядка или прямые.
x
124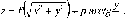
Поверхности вращения
Поверхности
вращения общего вида
Поверхность,
образованная вращением линии (плоской
или пространственной кривой) вокруг
неподвижной прямой - оси, называется
поверхностью общего вида (рис. 188 а).
Определитель поверхности может быть
записан следующим образом: W(a,
i)[a
вращается
вокруг i],
где
а
- образующая,
i
-
прямая (ось вращения). При вращении
каждая точка образующей описывает
окружность с центром на оси i;
плоскость
окружности перпендикулярна оси вращения.
Окружности,
описываемые точками образующей,
называются параллелями.
Наибольшая из параллелей - экватором,
наименьшая - горлом
или
горловиной.
Плоскости,
проходящие через ось вращения, называются
меридиональными,
а линии, по которым плоскости пересекают
поверхность, - меридианами.
Меридиональная
плоскость, параллельная плоскости
проекций, называется главной, а линия
пересечения ее с поверхностью - главным
меридианом.
Поверхность вращения считают закрытой,
если меридиональное сечение
поверхности является замкнутой кривой
линией, пересекающей ось поверхности
в двух точках.
Рис.
188
На
эпюре Монжа поверхности вращения
удобнее задавать очерками. Если ось
поверхности занимает горизонтально-проецирующее
положение, то горизонтальным очерком
поверхности является горизонтальная
проекция экватора 11
(рис. 188 б), а фронтальным очерком -
фронтальная проекция главного
меридиана а2.
Для построения точек, расположенных
на поверхности, рационально
использовать параллели. Видимость
точек на поверхности определяется
очерковыми линиями, ограничивающими
видимость самой поверхности
относительно плоскостей проекций.
125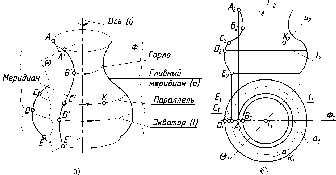
Поверхности
вращения частного вида
Такие
поверхности имеют в меридиональном
сечении кривую второ - го порядка или
две прямые, на которые распадаются
кривые второго порядка. По виду
главного меридиана и расположению оси
вращения поверхности вращения имеют
разные названия. На рис. 189 представлена
группа поверхностей, имеющих в качестве
образующей кривую второго порядка, а
в качестве оси вращения - проецирующую
прямую т.
Рассмотрим
подробнее эти поверхности.
Сфера.
Это поверхность, образованная вращением
окружности вокруг одного из своих
диаметров. Ось вращения проходит через
центр ок-
2
2 2 2
ружности.
Уравнение поверхности: x
+
y
+
z
=
r.
На
рис. 190 дан комплексный чертеж сферы,
заданной очерками. Пусть ось вращения
- горизонтально-проецирующая прямая,
тогда фронтальным очерком сферы
будет фронтальная проекция главного
меридиана а2,
а горизонтальным очерком - горизонтальная
проекция экватора b1.
Для
построения недостающих проекций К1
и К'1
точек К
и К',
расположенных на поверхности, используют
параллель. Видимость точек на поверхности
определяют на фронтальной плоскости
проекций П2
меридианом, а на П1
- экватором сферы. Невидимыми будут
точки за меридианом и под экватором.
Тор
открытый
(или круговое кольцо). Ось вращения не
пересекает образующую окружность, но
лежит в ее плоскости. Уравнение
поверхности:
{
2 2
2 2 ,2\2
л
2
/ 2 2\ >
(x
+
y
+
z
+
a
-
b)
= 4 a
(x + y),
где
а
>
b.
На
рис. 191
а
дана геометрическая часть определителя
кругового кольца. Зная, что каждая точка
линии а
описывает окружность, плоскость которой
перпендикулярна оси i,
а
центр расположен на оси, можно построить
очерки поверхности. На рис. 191 б заданы
очерки этой поверхности. По фронтальной
проекции точки К, расположенной на
поверхности, строят горизонтальные
проекции ее. Если известно, на видимой
части поверхности расположена точка
К
или на невидимой, то можно проводить
ее возможные параллели. В данном случае
возможны две параллели, пересекающие
образующую в двух точках 1
и 2,
следовательно, при положении К2
на поверхности возможны четыре положения
точек К1.
Тор
закрытый.
Ось вращения пересекает образующую
окружность, но не проходит через ее
центр (см. рис. 189). Уравнение поверхности:
I
2
, 2
, 2 2 «2\2
л
2/
2 2ч „ и
(x
+
y
+
z
+
а
- b)
= 4a
(x +
y),
где
а
< b.
Эллипсоид
вращения.
Поверхность, образованная вращением
эллипса вокруг своей оси. Поверхность,
образованная вращением вокруг малой
оси, называется сжатым
эллипсоидом вращения
(рис. 192 а), а вращением
вокруг
большой оси - вытянутым
эллипсоидом вращения
(рис. 192 б).
2
2 2 2 2 2 2
Уравнение
сжатого эллипсоида: а(х + y)
+
b
z
=
a
b .
Уравнение
вытянутого эллипсоида: b2(x2
+
y2)
+
a2z2
= a2b2.
126
t
> R
t
< R
t
= 0
тор
открытый
тор
закрытый
сфера
D
эллипсоид
сжатый
эллипсоид
вытянутый
однополостныи
гиперболоид
двухполостныи
гиперболоид
Рис.
189
127
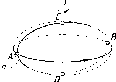

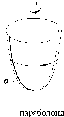
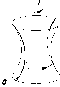

Параболоид
вращения.
Поверхность, образованная вращение
парабо-
2
2
лы
вокруг ее оси (рис. 193). Уравнение
поверхности: x
+
y
=
2pz.
Гиперболоид
вращения.
Поверхность, образованная вращением
гиперболы вокруг мнимой оси, называется
однополостным
гиперболоидом
вращения
(рис. 194 а). Поверхность, образованная
вращением гиперболы вокруг ее
действительной оси, называется
двухполостным
гиперболоидом
вращения
(рис. 194 б).
Уравнение
двухполостного гиперболоида вращения:
b2z
-
a2(x2
+
у) = a2b2.
Уравнение
однополостного гиперболоида вращения:
b2(x
+
y2)-
a2z2
=
a2b2.
Рис.
190 Рис.191
а)
б)
Рис.
192
Рис.193
128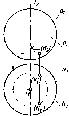
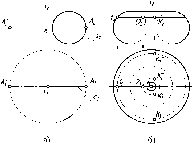
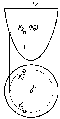
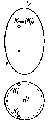
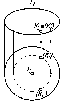
Рис.
194
Линейчатыге
поверхности вращения
Поверхности,
образованные вращением прямой линии
вокруг оси, также являются поверхностями
второго порядка. Возможны три случая
взаимного расположения образующей а
и оси i:
a
||
i;
а
@
i
и
а
□
i,
поэтому
возможны три вида поверхностей (рис.
195).
Рис.
195
129
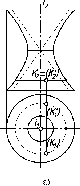
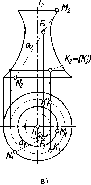
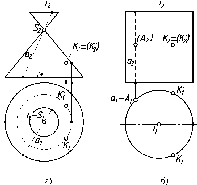
Коническая
поверхность вращения.
Образующая а
пересекает ось вращения i
в
точке S.
Если
ось вращения i
занимает
проецирующее положение (см. рис. 195
а), то для построения точки, расположенной
на поверхности, рационально построить
параллель. Если ось поверхности занимает
положение уровня (или общее), то для
построения точки на поверхности
удобно использовать образующую.
Уравнение
конуса вращения: z2
=
k2
(x2
+
y2).
Цилиндрическая
поверхность вращения.
Образующая а
параллельна оси вращения i.
Если
ось вращения - проецирующая прямая, то
получаем проецирующую поверхность
(см. рис. 195 б). Если ось занимает положение
уровня, то для построения точки на
поверхности необходимо использовать
не параллель, которая на одной из
плоскостей проекций изображается
в виде эллипса, а образующую.
Уравнение
цилиндра вращения: х2
+ у2
= г2.
Однополостный
гиперболоид вращения.
Прямая а
и ось вращения i
-
скрещивающиеся
прямые. На рис. 195 в показано построение
параллелей, описываемых верхней точкой
М
образующей а,
нижней точкой N
и
точкой F,
которая
описывает горловину. Кратчайшее
расстояние между скрещивающимися
прямыми определяет точку F.
Для
построения точки К
на поверхности используют параллель.
Определитель
линейчатой поверхности с тремя
направляющими имеет вид Ф (m,
n, l),
здесь
m,
n, l
- направляющие.
В
зависимости от формы направляющих и
их расположения в пространстве можно
получить разнообразные поверхности.
Некоторые из поверхностей этой
группы представлены на рис. 196.
Поверхность
косого цилиндра
с тремя направляющими образуется при
движении прямолинейной образующей по
трем криволинейным направляющим
(см. рис. 196 а). Такая поверхность может
быть задана проекциями трех
соответствующим образом подобранных
направляющих.
Поверхность
дваждыг косого цилиндра
(см. рис. 158).
Поверхность
дважды косого цилиндра образуется в
том случае, когда две из трех направляющих
кривые, а третья - прямая линия.
В
инженерной практике находят применение
частные случаи поверхности этого
вида, например, поверхность косого
клина. Эта поверхность получается
в том случае, когда все три направляющие
расположены в параллельных плоскостях,
причем криволинейные направляющие -
плавные кривые.
130Линейчатые неразвертываемые поверхности с тремя направляющими
Поверхность
косого клина используется при
конструировании поверхности крыла
летательного аппарата (см. рис. 196 б).
При этом достигаются не только
аэродинамические свойства крыла, но и
обеспечиваются хорошие технологические
условия изготовления его каркаса.
Рис.
196
Поверхность
однополостного гиперболоида
может быть получена при движении
прямолинейной образующей по трем
скрещивающимся прямым, не параллельным
одной плоскости.
На
рис. 196 в поверхность однополостного
гиперболоида задана прямыми направляющими
m,
n, l
и
показана образующая а, пересекающая
направляющие в точках M,
N, L.
Нелинейчатые
поверхности с образующей переменного
вида
Эта
группа поверхностей имеет определитель
Ф (а, m)
[A;
А1],
где
а
- образующая переменного вида,
m
-
направляющая,
А
- закон перемещения образующей по
направляющей,
Ai
-
закон изменения формы образующей.
Из
этой группы поверхностей можно выделить
поверхность общего вида, образованную
перемещением произвольной (плоской
или пространственной) кривой а,
по криволинейной направляющей b
(см.
рис. 159), и каналовую поверхность.
131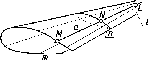

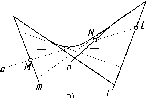
Каналовой
(рис. 197) называют поверхность, образованную
непрерывным каркасом замкнутых
плоских сечений, определенным образом
ориентированных в пространстве. Площади
этих сечений монотонно изменяются
в процессе их перемещения по направляющей
m.
У
поверхности, изображенной на рисунке,
плоскости образующих ориентированы
перпендикулярно направляющей.
Нелинейчатые
поверхности с образующей постоянного
вида
Определитель
такой поверхности имеет вид Ф (а , m)
[A],
где
а
-
образующая;
m
- направляющая;
А
- закон перемещения образующей.
Характерным
представителем этой группы поверхностей
можно назвать трубчатую (циклическую)
поверхность (рис. 198). Эту поверхность
можно отнести также к каналовой
поверхности, так как она содержит в
себе свойства, присущие последней
(см. рис. 197).
Поверхностью
параллельного переноса называют
поверхность, образованную поступательным
перемещением плоской линии. При этом
образующие поверхность линии все
время остаются параллельными между
собой.
Под
параллельными кривыми линиями
подразумеваются линии, получаемые
одна из другой путем параллельного
переноса принадлежащих им точек на
некоторое одинаковое расстояние.
Например, на рис. 199 кривая а'
параллельна кривой а,
так как точки А', А'1,
А'2
А'п
кривой а'
получены из точек А, А1,
А2
Ап
путем переноса их по параллельным
прямым на величину вектора d.
Рис.
197
Рис.
198
132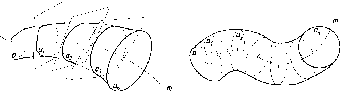
Поверхности параллельного переноса
В
общем виде поверхность переноса может
быть задана производящей линией а
в начальном ее положении и направляющей
(кривой линией m)
(рис.
200). Определитель такой поверхности
имеет вид Ф (а, m)
[A].
В
геометрическую часть определителя
входят образующая а
и направляющая m.
Алгоритмическая
часть состоит из условия параллельного
перемещения точек образующей (|| Е).
Рис.
199 Рис. 200
Нелинейчатая
поверхность, кривая образующая а
которой в процессе образования
поверхности произвольно изменяет свой
вид, называется графической
(рис. 201).
Форму
графической поверхности имеют корпуса
агрегатов, судов, двигательных аппаратов.
Графическая поверхность задается
некоторым числом линий, принадлежащих
этой поверхности. К разряду графических
относится топографическая (Topos
(греч.)
- местность, место) поверхность, т.е.
земная поверхность с точки зрения ее
изображений. Рельеф земной поверхности
передается линиями - горизонталями а,
получаемыми при пересечении этой
поверхности горизонтальными плоскостями
(рис. 202).
Рис.
201
Рис.
202
133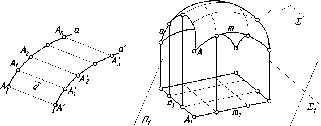
Графические и топографические поверхности
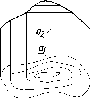
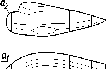
Задачи
на нахождение общих точек у прямой и
поверхности, построение линии
пересечения плоскости с поверхностью,
двух поверхностей определяют взаимное
положение геометрических образов и
относятся к классу позиционных.
Линия
пересечения поверхности с плоскостью
представляет собой, в общем случае,
плоскую кривую или ломаную линию, все
точки которой одновременно принадлежат
поверхности и секущей плоскости.
Аналитически
для определения уравнения линии
пересечения плоскости с поверхностью
необходимо решить следующую систему
уравнений:
Ах
+ By
+
Cz
+
D
=
0,
'
F
(x, y, z) =
0, (x,
y, z) e V,
где
V
-
пространственная
область.
134
Рис.
203Пересечение поверхности плоскостью и прямой, пересечение двух поверхностей
Пересечение поверхности плоскостью
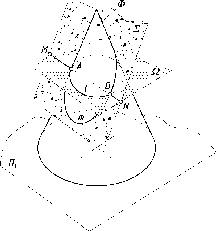
Для
графического построения точек линии
пересечения поверхности с плоскостью
используется общий способ нахождения
точек, принадлежащих двум геометрическим
образам - способ вспомогательных секущих
поверхностей. В качестве секущих
поверхностей используют вспомогательные
плоскости.
На
рис. 203 показана поверхность Ф и плоскость
Ъ, ее пересекающая. Для определения
точек искомой линии пересечения данных
геометрических образов используют
следующий алгоритм
решения:
заданные
геометрические образы рассекают
вспомогательной секущей плоскостью
W,
которую
выбирают так, чтобы она пересекла
поверхность по графически простым
линиям (прямым или окружностям);
находят
линии l
и
MN
пересечения
вспомогательной секущей плоскости Q
с
поверхностью Ф и плоскостью Ъ
соответственно;
определяют
точки А и В взаимного пересечения линий
l
и
MN,
лежащих
в секущей плоскости Q.
Точки
А
и В
принадлежат обоим геометрическим
образам, т.е. искомой линии пересечения
m;
последовательно
выбирают ряд секущих плоскостей,
построения при этом остаются теми же;
полученные
точки искомой линии пересечения
соединяют с учетом видимости.
До
начала построения необходимо сделать
анализ взаимного расположения
геометрических образов и искомой линии
их пересечения, рационально выбрать
вспомогательные секущие плоскости.
При
анализе искомой линии пересечения и
данных геометрических образов пользуются
следующими основными
положениями:
Плоскость,
пересекающая поверхность, может
занимать как общее, так и частное
положение относительно плоскостей
проекций.
Линия
пересечения криволинейной поверхности
с секущей плоскостью в общем случае -
кривая линия.
При
пересечении сферы любой плоскостью в
сечении всегда получается окружность.
Сечение
поверхности вращения плоскостью всегда
будет фигурой симметричной, ось
симметрии которой располагается в
общей плоскости симметрии двух
пересекающихся образов. Плоскостью
симметрии секущей плоскости является
любая плоскость, перпендикулярная ей.
Плоскость симметрии поверхности
вращения всегда проходит через ее ось.
Таким образом, общая плоскость симметрии
должна удовлетворять обоим условиям
- проходить через ось вращения поверхности
и быть перпендикулярной секущей
плоскости.
При
пересечении линейчатой поверхности
плоскостью точки искомой кривой
находятся как точки пересечения
образующих поверхности с данной
секущей плоскостью.
135
Линия
пересечения многогранной поверхности
с секущей плоскостью в общем случае -
ломаная линия, вершинами которой служат
точки пересечения ребер многогранной
поверхности с секущей плоскостью,
а сторонами - отрезки прямых пересечения
граней поверхности с той же плоскостью.
При
пересечении прямого кругового конуса
получается семейство различных
кривых второго порядка (конические
сечения) или прямые линии (образующие).
При
пересечении прямого кругового цилиндра
могут получаться окружности,
образующие или эллипсы.
У
цилиндрических, конических и
призматических поверхностей
выделяются так называемые нормальные
сечения. Нормальным называется
сечение цилиндра или призмы,
перпендикулярное образующим. Нормальное
сечение конуса - это сечение,
перпендикулярное его оси симметрии.
При
пересечении поверхности открытого
тора (кругового кольца) с плоскостью
получаются алгебраические кривые
четвертого порядка. Их общее название
- кривые Персея. На рис. 204 показаны
сечения поверхности открытого тора
различными плоскостями, которые
расположены на расстоянии l
от
оси тора.
В
зависимости от величин l,
R
и
г
кривые имеют различную форму:
две
окружности (см. рис. 204 а);
овалы
с одной осью симметрии (см. рис. 204 б);
двухлепестковая
кривая с узловой точкой в начале
координат (см. рис. 204 в);
волнообразная
кривая (см. рис. 204 г);
овал
с двумя осями симметрии (см. рис. 204 д).
Построение
линии пересечения следует начинать с
опорных
точек кривой.
Опорными точками кривой называют такие,
которые выделяются особым расположением
по отношению к плоскостям проекций или
занимают особое место на кривой.
Опорныти
точками являются:
точки
линии пересечения, лежащие на очерках
поверхности и называемые точками
изменения видимости. Проекции этих
точек делят проекцию линии пересечения
на видимую и невидимую части. Видимость
линии пересечения определяется по
видимости поверхности, на которой она
лежит. Видима всегда та часть
поверхности, которая ближе к наблюдателю;
экстремальные
точки линии пересечения, позволяющие
судить, в каких пределах следует строить
линию пересечения. К экстремальным
относятся самая дальняя и самая
ближняя точки, самая левая и самая
правая, наивысшая и наинизшая точки
линии пересечения, которые всегда
располагаются в общей плоскости
симметрии двух пересекающихся
геометрических образов;
136
-
характерные
точки закономерных кривых - это вершины
гиперболы или параболы, большая и
малая оси эллипса.
Остальные
точки линии пересечения называются
промежуточными. Следует помнить,
приведенная классификация опорных
точек условна. Экстремальные и характерные
точки одновременно могут являться и
точками изменения видимости.
Характерные точки могут определять
экстремальные положения линии
пересечения.
Приведенный
выше анализ задачи на пересечение
поверхности с плоскостью дает наиболее
общие закономерности, используемые
при решении. Особенно следует выделить
задачи построения нормальных сечений,
сечений прямых круговых конуса и
цилиндра, сечений линейчатых и
нелинейчатых поверхностей, сечений
плоскостями общего и частного положения.
137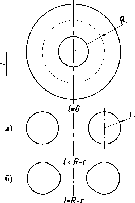
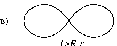
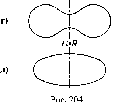
Сечение
поверхности проецирующей плоскостью
В
случае, когда секущая плоскость является
проецир^щей, построение линии
пересечения ее с поверхностью значительно
упрощается.
Из
рис. 203 видно, что линию l
пересечения
поверхности Ф со вспомогательной
секущей плоскостью W
можно
рассматривать как параллель, а точки
: и В - как точки пересечения этой
параллели с секущей плоскостью Е. Таким
образом, линия пересечения строится
как линия, лежащая на поверхности.
Одна из двух проекций искомой линии
пересечения совпадает со следом заданной
секущей плоскости и является прямой
линией. Вторая проекция строится по
точкам пересечения линий, лежащих на
поверхности (образующих или параллелей),
с заданной плоскостью.
Схема
нахождения точек линии пересечения
поверхности с плоскостью частного
положения приведена на рис. 205. Если
поверхность линейчатая, то каждая
точка искомой линии определяется как
точка пересечения прямолинейной
образующей поверхности с секущей
плоскостью.
На
рис. 205 а горизонтально проецирующая
плоскость 0 (0i)
рассекает
поверхность косой плоскости. Сначала
определяются горизонтальные проекции
искомых точек 11,
21,
а затем их фронтальные проекции на
соответствующих образующих.
На
рис. 205 б приведена схема нахождения
точек линии пересечения поверхности
вращения с фронтально-проецирующей
плоскостью Е (Е2).
Фронтальные проекции искомых точек
М2,
N2
определяются
при пересечении проекции параллели
Р2
со следом секущей плоскости Е2.
Горизонтальные проекции М1,
N1
лежат
соответственно на горизонтальной
проекции параллели Р1.
а)
б)
Рис.
205
138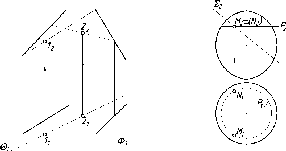
Построение
сечения
наклонного эллиптического конуса с
круговым
основанием
горизонтально-проецирующей плоскостью
Ъ (ЕД
показано на рис. 206.
Горизонтальная
проекция сечения совпадает с горизонтальным
следом плоскости Ъ1.
Для построения фронтальной проекции
сечения следует найти точки пересечения
образующих конуса с заданной плоскостью.
Начинать построения следует с опорных
точек.
Точки
изменения видимости располагаются на
образующих, дающих фронтальный очерк
поверхности - это образующие SA
и
SB.
На
пересечении 51Д со следом Ъ1
отмечается горизонтальная проекция
точки 11,
фронтальная проекция 12
точки 1 принадлежит фронтальной проекции
S2A2
образующей
SA.
Образующая
SB
не
пересекается с плоскостью в пределах
заданного конуса, поэтому линия
пересечения не имеет общих точек с
фронтальной очерковой образующей S2B2.
Самые
низкие точки кривой располагаются на
основании конуса. На горизонтальной
проекции отмечаются точки 21
и 31
на пересечении окружности основания
со следом Ъ1.
На фронтальной проекции основания
конуса по линиям связи строятся
фронтальные проекции 22,
32
точек 2 и 3. На горизонтальной проекции
точка 2 - видимая, а 3 - невидимая, так как
находится на нижней части конуса.
На фронтальной проекции точка 2 находится
на передней части конуса и будет видимой,
а точка 3 - на задней и будет невидимой.
Наивысшая
точка искомой кривой находится в общей
плоскости симметрии двух пересекающихся
г.о. Эта плоскость общего положения
проходит через центровую линию SO
конуса
перпендикулярно заданной плоскости
Ъ. На эпюре общая плоскость симметрии
задана двумя пересекающимися прямыми
SO
и
СО,
горизонтальная проекция которой С101
перпендикулярна
Ъ1.
Общая плоскость симметрии пересекает
конус по образующей SC,
на
горизонтальной проекции S1C1
которой
находится точка 41
в пересечении со следом Ъ1.
По линии связи определяется фронтальная
проекция 42
точки 4 на проекции образующей S2C2.
Точка
4 - наивысшая точка линии пересечения.
Горизонтальная
проекция крайней правой точки 51
находится на следе Ъ1
и образующей S1D1.
Фронтальная
проекция 52
строится по линии связи на S2D2.
Для
получения плавной кривой строится ряд
промежуточных точек, таких как точка
6.
Истинная величина сечения находится
проецированием на дополнительную
плоскость П4
|| Ъ1.
139
Рис.
206
140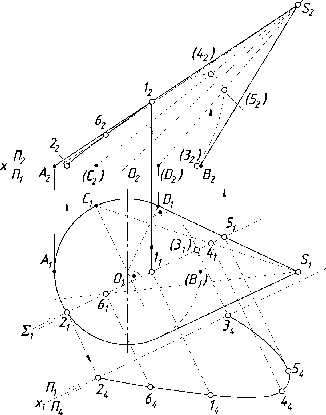
В
случае, когда секущая плоскость занимает
общее положение, схема построения
точек линии пересечения совпадает с
приведенным выше алгоритмом решения
задачи, проиллюстрированным на рис.
203.
В
соответствии с этим алгоритмом на рис.
207 показано нахождение точек линии
пересечения поверхности вращения с
плоскостью общего положения 0 (Д
ABC).
Вспомогательная
плоскость Г (Г2)
рассекает поверхность вращения по
параллели 1, а заданную плоскость 0 (Д
ABC)
по
горизонтали МК.
На фронтальной плоскости проекций
определяются фронтальные проекции
М2К2
и 12
линий МК
и 1, совпадающие со следом Г2.
На горизонтальной плоскости проекций
пересечение линии М1К1
с параллелью 11
даст проекции искомых точек N1
и
D1.
Фронтальные
проекции точек N
и
D
лежат
на следе Г2
плоскости Г.
олное
ре ение задачи на пересечение поверхности
конуса с плоскостью общего положения
приведено ниже (рис. 236).
141Сечение поверхности плоскостью общего положения
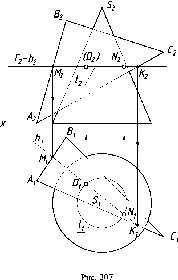
Рассмотрим
применение способа вспомогательных
секущих плоскостей для построения
линии сечения цилиндра плоскостью. На
рис. 208 заданы прямой круговой цилиндр
и плоскость Е (h
@
f)
общего положения.
Плоскость
Е (h
@
f)
пересекает цилиндр по эллипсу,
горизонтальная проекция которого
совпадает с горизонтальной проекцией
поверхности цилиндра - окружностью.
Это объясняется тем, что все образующие
цилиндра перпендикулярны П1,
а сама поверхность является горизонтально-
проецирующей. В качестве вспомогательных
секущих плоскостей следует применять
плоскости, параллельные или перпендикулярные
образующим цилиндра. Первые будут
пересекать цилиндр по образующим,
вторые - по окружностям.
Построение
линии пересечения начинают с опорных
точек.
Высшая
и низшая точки искомой кривой располагаются
в общей плоскости симметрии пересекающихся
геометрических образов. Такой плоскостью
является горизонтально-проецирующая
плоскость 0,
проходящая через ось вращения
цилиндра и перпендикулярная секущей
плоскости Е. Г оризонтальный след
01
этой плоскости проходит через i1
и
перпендикулярен горизонтальной
проекции горизонтали заданной плоскости,
то есть 01
±
h1.
Плоскость
0 (01)
пересекает цилиндр по образующим а
и b,
а
секущую плоскость Е (h
@
f)
по прямой ВК.
Горизонтальные
проекции а1
и b1
образующих
и В1К1
прямой совпадают со следом 01
общей плоскости симметрии. По линиям
связи строятся фронтальные проекции
а2,
b2
образующих
цилиндра и В2К2
прямой. При пересечении построенных
линий находятся общие точки 1
2
и 22
- фронтальные проекции самой высокой
2
и самой низкой 1
точек линии пересечения. Горизонтальные
проекции точек 1 и 2 совпадают с
горизонтальными проекциями образующих
а
и b.
Точки
изменения видимости линии пересечения
всегда располагаются на очерке
поверхности. Фронтальный очерк цилиндра
определяют образующие d
и
с. Для построения точек эллипса,
принадлежащих этим образующим,
вводится вспомогательная секущая
плоскость уровня Ф (Ф1).
След плоскости Ф1
проходит через горизонтальные проекции
d1
и
c1
образующих.
В сечении плоскости Ф (Ф1)
цилиндра получаются образующие d
и
с, в пересечении с данной плоскостью Е
- фронталь f'.
Фронтальная проекция f
'2
фронтали пересекает очерк цилиндра
(образующие d2,
c2)
в
точках 32
и 42,
которые являются точками изменения
видимости. Горизонтальные проекции
точек 3 и 4 совпадают с горизонтальными
проекциями образующих d
и
с.
Точки
изменения видимости 3 и 4 одновременно
являются самой левой и самой правой
точками линии пересечения.
142
ф"=
f'"
^1-4
Рис.
208
143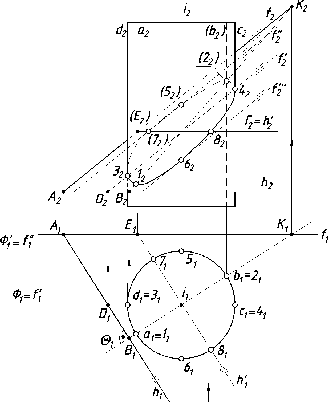
Для
определения самой дальней 5 и самой
ближней 6
точек эллипса проводятся вспомогательные
секущие плоскости уровня Ф' (Ф'Д и Ф"
(ФГ'). Обе секущие плоскости являются
касательными по отношению к цилиндру
и пересекают его по одной образующей.
Пересечение секущих плоскостей Ф' и Ф"
с заданной плоскостью Е происходит по
фронтали /''и /''' соответственно. Построение
искомых точек 5 и 6
аналогично приведенному выше
построению точек 3 и 4.
Для
получения плавной кривой строятся
промежуточные точки при помощи
горизонтальных плоскостей уровня,
которые рассекают цилиндр по окружностям,
а данную плоскость по горизонталям. На
рис. 208 построены промежуточные точки
эллипса 7 и 8,
лежащие в секущей плоскости Г(Г2).
Плоскость уровня Г(Г2)
пересекла заданную плоскость по
горизонтали h'.
Горизонтальная
проекция горизонтали h\
пересечет
окружность цилиндра в точках 71
и 81,
фронтальные проекции которых лежат на
следе Г2
плоскости Г.
Полученные
точки эллипса соединяют плавной кривой
с учетом видимости. На фронтальной
плоскости проекций видимой будет линия
на передней половине цилиндра до
образующих с
и d.
В
точках на очерке 32
и 42
видимость линии поменяется на
противоположную.
Ранее
было показано, что построение линии
пересечения поверхности с проецирующей
плоскостью значительно проще, чем с
плоскостью общего положения. Используя
методы преобразования эпюра, можно
секущую плоскость общего положения
преобразовать в проецирующую и построить
линию пересечения поверхности с
плоскостью частного положения.
Пример
такого преобразования приведен на рис.
209. Условие задачи соответствует задаче
пересечения цилиндра с плоскостью
общего положения (см. рис. 208).
Секущая
плоскость общего положения в новой
системе плоскостей проекций преобразована
так, что она стала проецирующей. На
новой плоскости проекций секущая
плоскость Е (h
@
f)
спроецировалась в след Е4
и, следовательно, проекция линии
пересечения цилиндра с плоскостью Е
совпадает со следом секущей плоскости.
На плоскости П4
сразу определяются высшая 2
и низшая 1
точки линии пересечения, лежащие в
общей плоскости симметрии 0
(01).
Если
известна проекция линии пересечения
на плоскости П4,
то можно построить недостающие ее
проекции при помощи образующих
цилиндрической поверхности. Однако
для нахождения точек изменения видимости
на кривой необходимо ввести вспомогательную
секущую плоскость Ф (Ф1),
как это сделано на рис. 208.
144
Рис.
209
145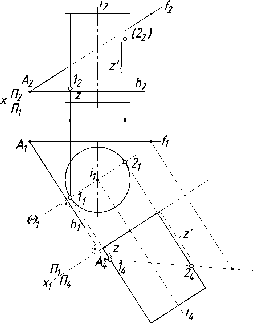
Конические
сечения
Из
многообразия конических поверхностей
выделяют поверхность прямого кругового
конуса, так как она обладает особыми
свойствами. Коническая поверхность,
кроме прямых линий (образующих), несет
на себе семейства различных кривых
второго порядка: эллипсов, окружностей,
парабол и гипербол. Эти кривые
получаются как конические сечения, то
есть являются линиями пересечения
поверхности конуса с плоскостями.
На
рис. 210 показаны сечения прямого кругового
конуса. В том случае, когда плоскость
Г (Г2)
пересекает все образующие конической
поверхности, в сечении получается
эллипс.
Частные случаи таких сечений - окружности,
когда секущая плоскость 0
(02)
пересекает все образующие и перпендикулярна
оси конуса, и точка S
-
вершина конуса, в которой пересекаются
все образующие.
Если
секущая плоскость Р (Р2)
параллельна одной из образующих
конической поверхности SA
и
пересекает одну полость конуса, то в
сечении будет получаться парабола.
Частным случаем такого пересечения,
когда секущая плоскость касается
конуса, является двойная прямая SA.
146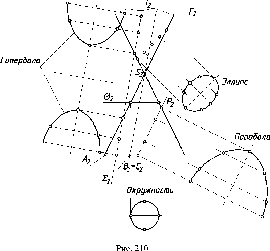
В
том случае, когда секущая плоскость Ъ
(Ъ2)
параллельна двум образующим SB
и
SC
и
пересекает две полости конической
поверхности, в сечении получается
гипербола
-
кривая, имеющая две ветви. В частном
случае, когда секущая плоскость Ъ (Ъ2)
проходит через вершину конуса S,
гипербола
вырождается в две пересекающиеся прямые
SB
и
SC.
Построение
линии пересечения прямого кругового
конуса с плоскостью частного положения
аналогично рассмотренным ранее задачам.
Полное решение такой задачи с нахождением
натуральной фигуры сечения приведено
ниже (рис. 236).
В
случае, когда рассматривается пересечение
конической поверхности второго
порядка и секущей плоскости общего
положения, также можно определить
вид линии пересечения. Для этого через
вершину конической поверхности
проводится плоскость, параллельная
заданной, и определяется вид
вырожденного сечения (примеры построения
не приводятся).
Нормальные
сечения
Нормальным
называется сечение цилиндра или призмы
плоскостью, перпендикулярной образующим.
Нормальное сечение конуса - это сечение,
перпендикулярное его оси симметрии.
Любой конус или цилиндр называется
всегда по нормальному сечению. Если
нормальное сечение - окружность, то
конус или цилиндр называются круговыми.
Если нормальным сечением является
эллипс, то поверхность называется
эллиптической.
Пример
построения нормального сечения призмы
приведен на рис. 211. Ребра трехгранной
призмы являются фронталями, поэтому
плоскость, им перпендикулярная, будет
фронтально-проецирующей Ъ (Ъ2)
±
П2
. Фронтальная проекция нормального
сечения 122232
совпадает со следом Ъ2,
горизонтальная проекция находится в
проекционной связи, каждая точка на
своем ребре. Таким образом, нормальное
сечение призмы - это треугольник
123, вершины которого определяются как
точки пересечения ребер с плоскостью
Ъ.
Для
конической поверхности (рис. 212) при
построении нормального сечения
необходимо определить ось конуса, как
линию пересечения двух плоскостей
симметрии Ф и Q.
Плоскость
Ф пересекает конус по образующим AS
и
BS,
а
плоскость Q
является
биссекторной плоскостью, проходящей
через биссектрису угла A2S2B2.
Нормальное
сечение - плоскость Ъ (Ъ2),
перпендикулярная оси конуса SN.
Ось
SN
есть
ось симметрии конической поверхности.
Линия SO
является
центровой, то есть геометрическим
местом центров семейства окружностей,
расположенных в плоскостях, параллельных
основанию. Название изображенного на
рис. 212 конуса - наклонный эллиптический
с круговым основанием. Конус называется
эллиптическим, т.к. нормальным
сечением его является эллипс.
147
На
рис. 213 показано построение нормального
сечения призмы, у которой ребра
занимают общее положение. Плоскость,
перпендикулярная прямой общего
положения, должна быть также общего
положения относительно плоскостей
проекций. Такую плоскость можно было
бы задать горизонталью и фронталью,
перпендикулярным ребрам, а затем три
раза решать задачу на пересечение
прямой с плоскостью общего положения.
Однако,
в данном случае приведено решение,
которое проецированием на дополнительную
плоскость сведено к частному, показанному
на рис. 211. В этом случае вводится новая
плоскость проекций П4,
перпендикулярная П1
и параллельная ребрам призмы, поэтому
ребра проецируются на П4
в натуральную величину. Плоскость Е
нормального сечения, перпендикулярная
ребрам в системе плоскостей П1П4,
будет проецирующей и изобразится в
виде следа Е4.
Нормальное
сечение 142434
совпадает со следом плоскости Е4,
зная его проекцию на П4,
строят недостающие горизонтальную и
фронтальную проекции сечения. Натуральная
величина сечения определена на
дополнительной плоскости проекций
П5ТП4
и параллельной следу Е4
плоскости нормального сечения Е.
148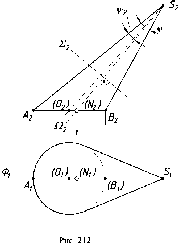
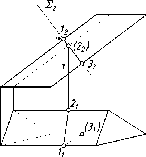
Рис.
213
149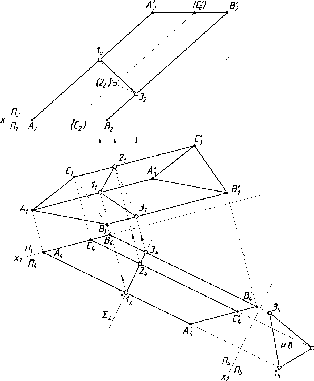
Плоскость,
касательная к поверхности
Положение
плоскости Е, касательной к поверхности
Ф в данной точке :, можно определить
двумя прямыми a
и
b,
каждая
из которых является касательной к
кривой, проведенной по поверхности
через точку :. На рис. 214 прямые а
и b
-
касательные к кривым n
и
m
соответственно.
Плоскость
может касаться поверхности либо в
точке, либо по линии (прямой или плоской
кривой). Касаясь поверхности в данной
точке, плоскость может пересекать
поверхность по одной или двум линиям.
На поверхности могут быть точки, в
которых нельзя провести касательную
плоскость. Такие точки называются
особыми. К их числу относятся точки
самопересечения поверхности, точки
ребра возврата, заостренные вершины
поверхностей вращения (когда образующая
пересекает ось вращения не под прямым
углом).
очки,
в котор х о но провести единственну
касательну плоскость, называют
обыкновенными.
Плоскость,
касательная к линейчатой поверхности
в произвольной точке на данной образующей,
проходит через эту образующую. Сказанное
объясняется тем, что каждая образующая
является своей собственной касательной.
Задача
построения касательной плоскости в
точке А
к поверхности однополостного гиперболоида
вращения приведена на рис. 215 а.
Однополосный
гиперболоид вращения - поверхность
дважды линейчатая. Через каждую
точку этой поверхности можно провести
две прямолинейные образующие. Они
и определят искомую плоскость.
Касаясь
поверхности в данной точке, эта плоскость
пересекает гиперболоид по двум
прямым. Горизонтальные проекции
прямолинейных образующих построены
как касательные к горловой окружности,
проведенные из :1.
Фронтальные проекции этих прямых
получены с помощью точек F
и
F,
в которых образующие пересекают нижнее
основание гиперболоида.
150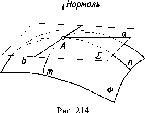
При
построении касательной плоскости к
нелинейчатой поверхности необходимо
через заданную точку провести на
поверхности две кривые. Касательные к
ним определят искомую плоскость.
На
рис. 215 б построена касательная плоскость
к поверхности вращения в данной на
ней точке А.
В
качестве кривых, проходящих по поверхности
через точку А, целесообразно взять
параллель и меридиан. Касательная к
первой - прямая АВ, находясь в одной
горизонтальной плоскости с рассматриваемой
параллелью, проецируется на П2
в прямую, параллельную оси о, а на П1
- в виде касательной к окружности радиуса
г. Для построения второй прямой
(касательной к меридиану) повернем
меридиан вокруг оси i
до
совмещения с главным меридианом. Точка
А при этом займет положение А'. Проведем
через точку А' касательную к главному
меридиану и продолжим ее до пересечения
с осью i
в
точке С или до М на плоскости П1
(одна из этих точек всегда может быть
найдена в пределах чертежа.).
Теперь
остается перевести меридиан и построенную
касательную в первоначальное положение.
Соединяя точку А с С или с М, получим
вторую прямую СМ,
которая, пересекаясь с АВ, определяет
искомую касательную плоскость.
а) б)
Рис.
215
151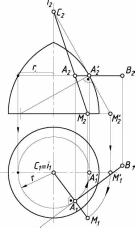
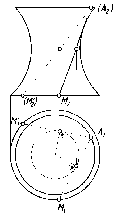
налитически
для определения координат точек
пересечения пря ой линии с поверхностью
необходимо решить следующую систему
уравнений: (г
:1
o +<1
y
+C1
z +
D1
=
0,
A2
x
+ B2
y + C2
z + D2
=
0,
F
(x, y
z) = 0,
(x, y,
z,) e V,
где
V-
пространственная
область.
Ерафическое
решение задачи на определение точек
пересечения прямой линии с поверхностью
аналогично задаче нахождения точки
пересечения прямой линии с плоскостью.
Точки пересечения прямой линии с
поверхностью определяются способом
вспомогательных секущих плоскостей.
Алгоритм решения задачи следующий:
через
прямую а
проводится вспомогательная плоскость
Е (рис. 216);
находится
линия пересечения l
вспомогательной
плоскости Е с данной поверхностью W;
на
пересечении полученной линии пересечения
l
с
заданной прямой а
найдутся искомые точки М
и N;
определяется
видимость прямой.
Рис.
216
Через
прямую можно провести сколько угодно
различных плоскостей, однако для
упрощения решения задачи надо выбирать
такую вспомогательную плоскость, в
пересечении которой с данной поверхностью
получились бы простые линии (прямые
или окружности). Вспомогательная
плоскость Е может занимать как общее,
так и частное положение относительно
плоскостей проекций. Примеры рационального
выбора вспомогательной секущей
плоскости, занимающей частное положение,
приведены на рис. 217.
152Пересечение прямой линии с поверхностью
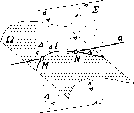
На
рис. 217 а, задана горизонтально -
проецирующая прямая ш, пересекающая
поверхность конуса. Вспомогательная
секущая плоскость Е (Е^ проведена через
горизонтальную проекцию ш1
прямой ш
и через проекцию вершины конуса 51. Эта
плоскость Е (Е1)
пересекает поверхность конуса по двум
образующим. При пересечении фронтальной
проекции образующей K2S2
с
проекцией ш2
данной прямой находится фронтальная
проекция А2
искомой
точки пересечения. Горизонтальная
проекция А1
точки А совпадает с проекцией ш1
данной прямой ш.
Рис.
217
На
рис. 217 б, решена задача на пересечение
горизонтали h
с
поверхностью сферы. Через горизонталь
h
проведена
горизонтальная плоскость уровня
Г(Г2),
которая пересекает сферу по окружности
1.
Фронтальная проекция 12
окружности совпадает со следом Г2
секущей плоскости Г, горизонтальная
проекция окружности 11
изображается на плоскости П1
в истинную величину. Точки М1,
N1
ее
пересечения с проекцией h1
горизонтали
есть горизонтальные проекции искомых
точек встречи горизонтали с поверхностью
сферы. Фронтальные проекции М2,
N2
точек
М и N
лежат
на фронтальной проекции h2
горизонтали
h.
На
горизонтальной плоскости проекции
точки М1
и N1
невидимы,
так как находятся ниже экватора (в
нижней части сферы). Часть прямой от
точек М1
и N1
до
экватора невидима. На фронтальной
плоскости точка М2
видима, так как находится на передней
части сферы, поэтому прямая слева от
точки М2
видима. Точка N2
невидима,
так как находится за главным меридианом,
поэтому часть прямой от точки N2
до
главного меридиана невидима. Часть
прямой между точками М и N
пропадает
внутри сферы.
153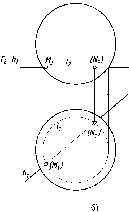
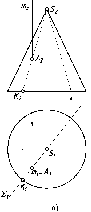
На
рис. 218 приведена задача на построение
точек пересечения прямой с поверхностью
вращения. В качестве вспомогательной
секущей плоскости выбрана
горизонтально-проецирующая плоскость
Е (Е1),
которая проходит через данную прямую
а
и пересекает поверхность вращения по
кривой линии т. Горизонтальная проекция
кривой m1
совпадает
с горизонтальным следом Е1
плоскости Е.
Для
построения фронтальной проекции т2
кривой на поверхности вращения проводятся
параллели - окружности соответствующих
радиусов. Фронтальная проекция т2
кривой т
строится как линия, принадлежащая
поверхности. Каждая точка кривой т
лежит на своей параллели. Проекции
искомых точек Ми N
пересечения
данной прямой а
с поверхностью вращения определятся
на фронтальной плоскости проекций при
пересечении фронтальной проекции т2
кривой т
с проекцией заданной прямой а2.
Горизонтальные проекции М1
и N1
искомых
точек находятся по линиям связи на
проекции а1
заданной прямой а.
На
горизонтальной плоскости проекций
точки М1
и N1
видимы.
На фронтальной плоскости проекция
точки N2
видима,
так как находится перед главным
меридианом (на передней части поверхности
вращения), а точка М2
невидима, так как находится за главным
меридианом (с обратной стороны
поверхности).
Во
всех приведенных выше задачах
вспомогательная секущая плоскость
занимает частное положение. Вспомогательную
плоскость общего положения удобно
использовать в задачах при пересечении
прямой линии с конической или
цилиндрической поверхностью. При
пересечении цилиндрической поверхности
прямой линией вспомогательную плоскость
проводят через данную прямую параллельно
образующим цилиндра. В этом случае в
сечении плоскости с цилиндром получаются
прямые линии.
Пример
решения задачи на пересечение прямой
с цилиндром приведен на рис. 219. Задан
наклонный цилиндр с круговыми основаниями.
Для построения точек пересечения
поверхности цилиндра с прямой линией
АВ проводят плоскость W,
определяемую
данной прямой АВ и прямой ВМ, проведенной
через точку В параллельно образующим
цилиндра. Плоскость W
(АВ@ВМ)
пересекает цилиндр по образующим. Если
найти горизонтальные следы прямых
АВ и ВМ, то через горизонтальные проекции
следов прямых 11
и 21
может быть проведен горизонтальный
след W1
плоскости
W.
Горизонтальный
след W
пересекает
основание цилиндра в точках 31
и 41,
через которые проводят проекции
образующих цилиндра. Там, где проекции
образующих пересекают проекцию А1В1
данной прямой, определяют проекции D1,
L1
искомых
точек пересечения прямой АВ с поверхностью
цилиндра. Проекции D2,
L2
искомых
точек D
и
L
лежат
на фронтальной проекции прямой АВ.
Видимость точек пересечения D
и
L
определяют
в соответствии с видимостью образующих,
на которых лежат эти точки.
154
При
решении задачи на пересечение поверхности
прямой линией
может оказаться, что
данная прямая не пересекает, но лишь
касается дан-
ной
поверхности со вспомогательной
плоскостью.
В этом случае прямая явля-
ется
касательной к данной поверхности
(рис.
220). На этом рисунке через гори-
зонтальную
проекцию А1В1
прямой АВ
проведена
горизонтально-проецирующая
вспомогательная
секущая плоскость
И (Hi),
которая
пересекает сферу по ок-
ружности
радиусом г.
Истинная величи-
на окружности
построена на плоскости
П4,
где определится и проекция К4
точки
касания К прямой с поверхностью
сфе-
ры.
Вообще,
если требуется опреде-
лить, как
прямая расположена относи-
тельно
поверхности, надо через прямую
провести
плоскость, пересекающую по-
верхность,
и рассмотреть взаимное по-
ложение
прямой и фигуры, полученной
при
пересечении поверхности плоско-
стью.
В,
Рис.
220
155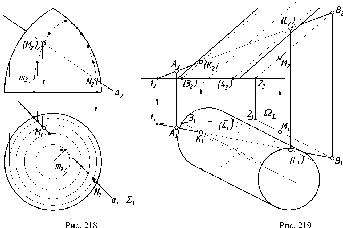
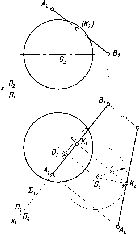
Геометрическое
место точек, принадлежащее одновременно
двум поверхностям, называют линией
пересечения (или линией перехода)
данных поверхностей.
Рис.
223 Рис. 224
Линия
пересечения двух поверхностей в общем
случае представляет собой пространственную
кривую. При частичном пересечении
поверхностей (одна из поверхностей
как бы «врезается» в другую) будет одна
замкнутая линия пересечения (рис.
221). При полном пересечении поверхностей
(одна из поверхностей пересекает другую
насквозь) получаются две замкнутые
линии пересечения (рис. 222). В случае
двух многогранных поверхностей
линия их пересечения является ломаной
линией (рис. 223). Если одна из поверхностей
кривая, а другая - гранная, то линия их
пересечения представляет собой
плоскую кривую линию или ее часть (рис.
224).
Обычно
линию пересечения двух поверхностей
строят по ее отдельным точкам, которые
аналитически определяются при решении
системы уравнений:
Г
f
(x, y, z) =
0,
L
f
' (x, y, z) =
0.
156Пересечение поверхностей
Общие сведения
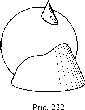

В
начертательной геометрии задачу на
пересечение двух поверхностей решают
путем введения вспомогательных секущих
поверхностей- посредников. В качестве
поверхностей-посредников применяют
плоскости или сферы, поэтому различают
способ вспомогательных секущих
плоскостей и способ вспомогательных
секущих сфер. Последний имеет
разновидности: способ концентрических
сфер и способ эксцентрических сфер.
Применение того или иного способа
зависит как от типа данных поверхностей,
так и от их взаимного расположения.
Построение
общих точек, принадлежащих линии
перехода поверхностей, поясняется
на рис. 225 и осуществляется по общему
для всех способов алгоритму:
выбирают
секущие поверхности-посредники
А
1 относительно
данных поверхностей Р, Т такими, чтобы
в пересечении получались графически
простые линии (прямые, окружности) и
чтобы проекции этих линий легко
строились на эпюре;
строят линии m и п, по которым посредник пересечет обе поверхности;
находят общие точки : и В пересечения линий m и п. Эти точки принадлежат одному посреднику и одновременно двум данным поверхностям;