Материалы для студ 3 курса каф РЭС / Материалы 2013_2014уч. г / Лекции по ЭДиРРВ для 3 курса 2013 / Курс лекций Звездиной по ЭДиРРВ

121

Раздел 5. ДИФРАКЦИЯ ЭЛЕКТРОМАГНИТНЫХ ВОЛН

5.1. Электродинамические задачи дифракции

Строгая постановка дифракционных задач. Метод разделения переменных.

Дифракция электромагнитных волн на бесконечном идеально проводящем круглом цилиндре.

5.1.1.При своем распространении электромагнитные волны сталкиваются

стелами, расположенными как вблизи, так и вдали от источников электромаг- нитного поля. При этом наблюдается огибание и отражение электромагнитной волной от поверхности тела, что приводит к изменению структуры излученного источником поля. Явление изменения структуры поля первичной волны при падении ее на тело называется дифракцией.

Волна называется первичной, если она возбуждается сторонними токами, возникающими в результате действия источников, имеющих неэлектромагнит- ную природу, или является приходящей из бесконечности. Рассеянное телом электромагнитное поле будем называть вторичной волной. Данное разделение основывается на причинно-следственной связи и является условным. Сумма первичного и вторичного полей называется полным полем.

Исследования явлений дифракции на реальных телах, имеющих различ- ные конфигурации, размеры и другие параметры, можно проводить аналитиче- скими и численными методами, а также экспериментально. При этом точные аналитические методы решения дифракционных задач, полученные в замкну- той форме, предполагают решение дифференциальных уравнений в частных производных в той системе координат, в которой координатные поверхности совпадали или были близки к граничным поверхностям. Данные поверхности получили называние канонических. При указанных условиях возможно разде- ление компонент электрического и магнитного полей.

Примерами канонических поверхностей являются, в частности, круговой, эллиптический, параболический цилиндры, бесконечный клин, сфера. Полу-

ченные для канонических поверхностей решения могут играть роль эталонных

123

или произведения сумм неизвестных функций M (x), N (y), каждая из которых зависит только от одной координаты. Подставив выражение (5.2) в уравнение

Появление постоянной разделения K 2 обусловлено тем, что левая и правая части уравнения зависят от разных переменных. Уравнение (5.3) может быть разделено на два обыкновенных дифференциальных уравнения:

При обратном сочетании знаков при постоянной разделения гиперболические и тригонометрические функции меняются местами.

При решении сначала находится та независимая функция, по переменной которой заданы нулевые граничные условия, например, M (x) . Данная функция

будет удовлетворять заданным однородным граничным условиям и не будет равна нулю (что не представляет интереса) только при определенных значениях чисел Kn . Числа Kn в общем случае вычисляют, приравнивая к нулю главный определитель системы уравнений, полученной путем подстановки решения

M n (Kx) в выражение для граничных условий (при x = a и x = b). Определи-

тель составляют из коэффициентов при An и Bn , которые рассматривают как искомые величины. Затем какое-либо значение из найденных чисел Kn под-

ставляют в эту систему уравнений и находят одну из постоянных, например, A,

выраженную через B. Однако числа Kn в ряде случаев могут быть рассчитаны без составления системы уравнений, непосредственно по граничным условиям,

124

с учетом свойств искомого поля. При известных значениях Kn частное реше-

ние имеет вид:

∞

ψ (x, y) = å{(An cos Kn x + Bn sin Kn x)(Cn ch Kn y + Dn sh Kn y)}. (5.6)

n=1

Постоянные Cn , Dn определяют из неоднородных граничных условий по пере-

менной y.

5.1.2. Рассмотрим получение точного решения для одной из канонических поверхностей – бесконечного круглого (кругового) цилиндра - с использовани- ем метода разделения переменных.

Постановка задачи звучит следующим образом.

Пусть на бесконечный круговой цилиндр радиуса a падает плоская электромаг- нитная волна, распространяющаяся в направлении, перпендикулярном обра- зующей цилиндра.

Требуется определить вторичное электромагнитное поле, возникающее в про- странстве, при условии, что на поверхности выполняются граничные условия для идеально проводящего тела.

Решение будем искать в цилиндрической системе координат, ось 0z ко- торой параллельна образующей цилиндра.

При решении поставленной задачи целесообразно рассматривать два слу- чая поляризации падающей волны относительно оси 0z :

1)вектор E параллелен оси 0z ;

2)вектор H параллелен оси 0z .

Общий случай произвольной

поляризации падающей волны может быть получен суперпозицией данных типов полей.

Так как методика решения обеих задач одинакова, ограничимся анализом только

125

В соответствии с исходными данными проекции векторов поля падающей волны будут иметь вид:

Поперечные компоненты поля, как было показано при рассмотрении регуляр- ных линий передачи электромагнитной энергии, могут быть получены на осно- ве уравнений Максвелла через продольные составляющие поля.

Строгое решение дифракционной задачи сводится к решению уравнений Максвелла при заданных граничных условиях для составляющих электромаг- нитного поля на поверхности цилиндра и на бесконечности. В качестве гранич-

ных условий выступает требование непрерывности касательных к поверхности цилиндра составляющих векторов результирующего электромагнитного поля на поверхности цилиндра. На бесконечности вторичное поле должно удовле- творять принципу излучения (условиям Зоммерфельда).

По определению, если падающее поле содержит продольную компоненту электрического поля, т.е. является поперечно-электрическим, то и дифракцион- ное поле должно быть поперечно-электрическим.

Рассеянное поле удовлетворяет двумерному уравнению Гельмгольца, ко-

торое в цилиндрической системе координат имеет вид

Граничное условие для полного поля на поверхности определяется выра-

жением

При использовании метода разделения переменных в виде произведения двух функций, зависящих только от r и только от ϕ

126

уравнение (5.8) распадается на два обыкновенных дифференциальных уравне-

ния

где m – постоянная разделения.

Как известно, решение дифференциального уравнения (5.11б) имеет вид

Представим падающее поле в виде известного из теории бесселевых функций разложения

рядка.

С учетом того, что зависимость Еz в падающем поле в формуле (5.13) представляет собой четную функцию, то в соотношении (5.12) необходимо ос- тавить только первое слагаемое и положить C2 =0. Число m должно быть целым, чтобы функция из (5.12) и ее производная были непрерывны во всей области

[0,2p].

После того как определена целочисленность m, получаем, что (5.11а) есть уравнение для цилиндрической функции порядка m от аргумента kr. Общее ре- шение данного уравнения, называющегося уравнением Бесселя, имеет вид:

127

В данных соотношениях Hm(1) (×), Hm(2) (×) - функции Ганкеля соответственно 1-го и 2-го рода m-го порядка, рассмотренные ранее при изучении цилиндрических волн и функции Грина; Ym (×) – функция Неймана m-го порядка.

Для выбора решения используем условие излучения. В соответствии с данным условием искомое поле должно иметь характер волны, распростра- няющейся в бесконечность по радиальным направлениям. Из рассмотрения асимптотических выражений для функций Ганкеля:

справедливых при больших значениях аргументов z >>1; z >> m, следует,

что слагаемое BmHm(2) (kr) из (14б) при kr → ∞ соответствует волне, распро-

страняющейся от источника (в данном случае цилиндра) на бесконечность, т.е. удовлетворяет условию излучения.

Таким образом, решение однородного уравнения Гельмгольца ищем в виде

Коэффициенты Bm можно найти из последнего неиспользованного условия за- дачи – граничного условия (5.9), которое приводит к простому функциональ- ному уравнению:

которое должно выполняться для всех ϕ. Функции cosmϕ образуют полную ор- тогональную систему. Домножим каждое из слагаемых в левой части (5.17) на cosnϕ и проинтегрируем в пределах [0, 2π]. Ортогональность функций означает,

что

129

Вынесем знаменатель за скобку, а к скобке применим определение вронскиана, учитывая, что ток ищется на поверхности цилиндра, т.е. r = a :

В результате получаем следующее выражение для продольной компоненты вектора плотности поверхностного электрического тока, возбуждаемого на поверхности идеально проводящего кругового цилиндра поперечно-электрической электромаг- нитной волной, приходящей перпендикулярно образующей цилиндра:

Суммирование в формуле (5.25) проводится до значений m, близких к величине

2ka .

Повторяя аналогичные рассуждения для второй поляризации и учитывая, что граничные условия в данном случае будут иметь вид:

запишем сразу уравнение для нахождения коэффициентов дифракции:

Решая данное уравнение, получаем следующее выражение для коэффициента дифракции:

∂Jm (ka)

∂a

Соотношение для возбуждаемого поверхностного тока при этом прини- мает вид:

130

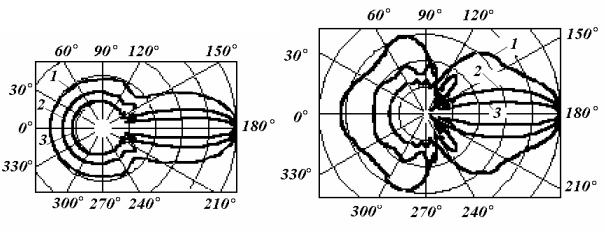
Графики нормированных диаграмм рассеяния для идеально проводящего цилиндра при различных значениях ka в полярной системе координат приведе- ны на рисунке 5.2 (Е-поляризация) и рисунке 5.3 (Н-поляризация). Кривые с номерами 1 соответствуют ka=3,14, с номерами 2 – ka=6,28, с номерами 3 – ka=12.

Рисунок 5.2 Рисунок 5.3

Из графиков следует, что с увеличением электрического радиуса цилинд-

ра растет уровень поля в направлении распространения волны (ϕ=180°), лепе- сток диаграммы рассеяния, максимум которого ориентирован в данном направ- лении, с ростом ka становится все уже. Аналогичные выводы справедливы и для случая Н-поляризованной волны.

Следует отметить, что представление решения данной краевой задачи ме- тодом разделения в виде ряда было впервые получено в 1882г. Рэлеем, а сами ряды получили называния рядов Рэлея.

В настоящее время рядом Рэлея называется бесконечная линейная ком- бинация элементарных волн, имеющих только одно из возможных направлений распространения в выбранной системе координат. Под элементарными вол-

нами понимаются частные решения однородных стационарных волновых уравнений в свободном пространстве в заданной криволинейной ортогональной системе координат. Обычно ими являются цилиндрические, сферические или плоские волны.