экзамены и коллоквиумы / Обяхательные вопросы к коллоквиуму 3

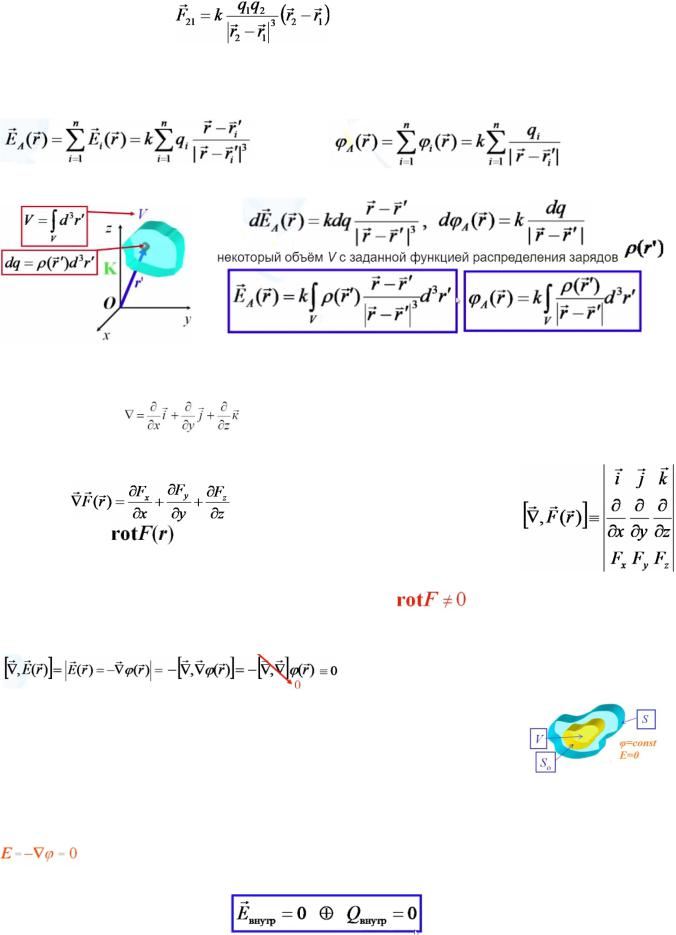
1.Закон Кулона (формула)

2.Основная задача электростатики (для точечных зарядов в вакууме, для произвольного объёмного распределения зарядов в вакууме и диэлектрике)

Для системы точечных зарядов в вакууме по принципу суперпозиции:

Для зарядов с непрерывным распределением в объёме:

Вектор эл-го смещения (в-р индукции) 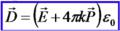3. Дифференциальные операторы (оператор набла, дивергенция функции, ротор функции)

Оператор набла формальный вектор, компоненты которого - некоторые объекты, желающие взять частную производную от функции.

Дивергенция функции - 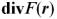- скалярное произведение оператора набла на векторную функцию.

4. Безвихревой характер электростатического поля.

Вихревое поле – векторное поле F, ротор которого не равен 0 (нет источников, силовые линии замкнуты на себя)

Электростатическое поле - безвихревое – ротор напряженности равен 0

Силовые линии никогда не замыкаются сами на себя, начинаются или заканчиваются на заряде.

5. Свойства проводников.

Определение для электростатики:

Проводник - называть любое тело, все точки которого в стационарных условиях и в отсутствии внешних изменяющихся во времени эл-х полей имеют одинаковый потенциал.

Следовательно напряжённость электростатического поля внутри проводника равна нулю -

Внутри проводника ЗАРЯДОВ НЕТ -» распределяются только по ПОВЕРХНОСТИ ПРОВОДНИКА

Получается всегда ( и в поле, и вне)

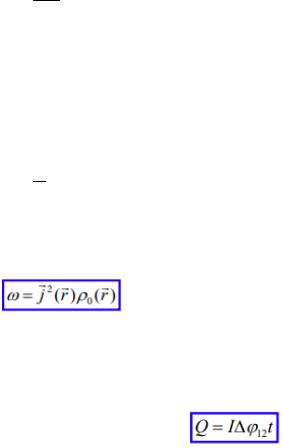
7. Интегральные законы ома (для участка цепи, содержащего ЭДС - определение ЭДС и сопротивления участка цепи; для замкнутого проводника; для участка цепи, не содержащего ЭДС)

12 = 12 + 12 - Интегральный закон Ома для участка цепи, содержащего ЭДС.

ЭДС – скалярная физическая величина, характеризующая работу сторонних сил, то есть любых сил неэлектрического происхождения, действующих в квазистационарных цепях постоянного или переменного тока.

В замкнутом проводящем контуре ЭДС равна работе этих сил по перемещению единичного положительного заряда вдоль всего контура.

Сопротивление участка цепи – физическая величина, которая показывает способность проводника пропускать электрический ток.

Для замкнутого проводника, очевидно 12 = 0, и мы получаем интегральный закон Ома для замкнутой цепи

=

0+

Здесь R12=R0+r, причем R0 – сопротивление внешней цепи, r – (внутреннее) сопротивление ЭДС, ε – алгебраическая сумма всех ЭДС в цепи.

Если ε12=0 – то получается интегральный закон Ома для участка цепи, не содержащего ЭДС.

8. Закон Ома в дифференциальной форме:

= = , где 0 = 1/0 – удельная проводимость

Плотность тока в любой точке проводника пропорциональна напряженности электрического поля в этой точке

9. Тепловое действие тока (закон Джоуля-Ленца в дифференциальной и интегральной формах)

- закон Джоуля-Ленца в дифференциальной форме

Формулировка:

Удельная мощность тока, выделяемая в окрестности данной точки проводника (т.е. в элементарном объеме с радиус-вектором r пропорциональна квадрату плотности тока в этой точке.

Интегрируя, получим Закон