экзамены и коллоквиумы / Вопросы на экзамен к вопросам коллоквиума

Вопросы на экзамен

1. Корпускулярно-волновой дуализм - постулат Л. Де Бройля (эксперименты по дифракции электронов)

К орпускулярно-волновой дуализм - двойственность свойств электромагнитного излучения – может проявлять как волновые свойства, так и свойства частиц(корпускулярные)

Постулат Л. Де Бройля – любую микрочастицу можно моделировать волновым процессом с длиной волны. ,где h – постоянная Планка, р – относительный импульс микрочастицы.

Эксперимент: Нейтрон – частица, но после взаимодействия с кристаллом летит в строго определённое место. в любом случае каждая частица даёт точку, но они расположены так, как должна располагаться электромагнитная волна – по окружностям вокруг центра пучка, м/у ними попасть не может

2. Уравнение Шредингера (стационарное и нестационарное)

Уравнение Шредингера – ур-е, описывающее поведение микрочастицы массой m во внешнем силовом поле.

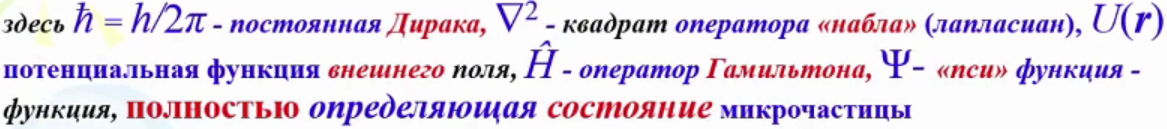Нестационарные состояния микрочастицы – в которых могут меняться все динамические параметры. Нестационарное уравнение Шредингера:

С тационарные состояния микрочастицы – в которых допускает представление в виде функции только от координат и функции экспоненты от времени. Стационарное уравнение Шредингера

3. Физический смысл Ψ-функции – физ. смысл имеет не сама функция, а квадрат её модуля – равен плотности вероятности нахождения частицы в элементарном объёме.

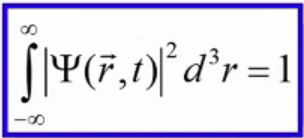Условие нормировки Пси-функции, чтобы стационарное уравнение имело дискретные решения.

- из него находится амплитуда Пси-функции, где

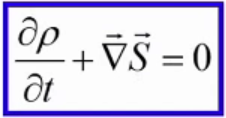
Ф изический смысл Пси-функции – закон сохранения вероятности

, где ,а - плотность тока вероятности

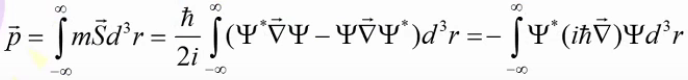Импульс

• 

4 . Основной постулат квантовой механики Любой физической величине можно поставить в соответствие линейный самосопряженный оператор так, что спектр собственных значений оператора совпадёт со спектром допустимых значений физ. величины. Оператор – правило, по которому одной функции сопоставляется другая функция. Самосопряженный оператор – оператор, собственные значения которого действительные

5. Правила сопоставления операторов - правила сопоставления Неймана

Нейман доказал - сопоставление физ. величине линейного самосопр-ного оператора взаимно-однозначно.

1. Если физ. величине S1 ставится в соответствие оператор Ŝ1, а физ. величине S2 ставится в соответствие оператор Ŝ2, то сумме этих физ. величин сопоставляется сумма этих операторов.

2. Если физ. величине S ставится в соответствие оператор Ŝ, то физ. величине S умноженной на коэфф-т не являющийся динамической переменной ставится в соответствие оператор Ŝ умноженный на этот коэфф-т.

3. Если физ. величине S ставится в соответствие оператор Ŝ, то гладкой скалярной функции от этой физ. величины будет сопоставляться та же сама гладкая функция от этого оператора.

4. Единичной физ. величине ставится в соответствие единичный оператор.

Принцип соответствия Неймана – операторы, сопоставляемые физ. величинам, подчиняются тем же соотношениям, что и сами физ. величины.

6. Правила сопоставления операторов - практический рецепт (операторы импульса и координаты)

П о основному постулату – среднее значение любой физ. величины с известной Пси-функцией вычисляется через оператор этой физической величины.

З начит, Оператор импульса «по уравнению»

Оператор координаты – сам радиус-вектор

П рактический рецепт сопоставления операторов – если физическая величина имеет классические аналоги, то для сопоставления ей оператора нужно представить эту величину как функцию координаты и импульса. 7. Уравнение квантования: Почти всегда получится дифференциальное уравнение

То есть Оператор физ. величины на Пси-функцию = собственному значению этого оператора на Пси-функцию.

Е сли выполняется условие нормировки, то уравнение квантования имеет решения лишь при некоторых собственных значениях оператора

С пектр оператора - множество его собственных значений

Собственные функции оператора - соответствующие Пси-функции

8. Проблема измерения в квантовой механике - условие коммутации

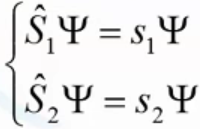
Е сли значения нескольких физ. величин S1 и S2 измеримы сколь угодно точно, ,то Пси-функция является собственной функцией операторов Ŝ1 и Ŝ2, т.е. =» =» Действие 1-го оператора, а потом 2-го на Пси-функцию = действию сперва 1-го о., а потом 2-го

9. Проблема измерения в квантовой механике - соотношение неопределенностей Гейзенберга

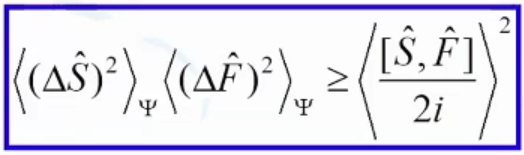П роизведение квадрата оператора погрешности измерения Одной физ. величины в заданном квантовом состоянии на квадрат оператора погрешности измерения Другой физ. величины всегда больше квадрата среднего значения коммутатора этих величин.

,где 10. Проблема измерения в квантовой механике - парадокс Эйнштейна - Подольского – Розена

- Пусть две одинаковые частицы А и В образовались в результате распада частицы С - Тогда по ЗСИ их суммарный импульс равен импульсу ч. С =» Рс=Ра+Рв - Измерим импульс ч. А и найдём импульс ч. В =» Рв=Рс-Ра - Измерив координату ч. В – Хв, получим точные значения двух некоммутирующих величин импульса Рв и координаты Хв — Это НЕВОЗМОЖНО