Ориентированные графы

• Обобщение теоремы Дирака. Пусть есть сильно связный ориентированный граф с n вершинами, входящая и исходящая степень любой вершины которого больше или равна n/2. Тогда в данном графе существует гамильтонов цикл.

• Определение. Турниром T называется орграф, любые две вершины которого соединены ровно одним ориентированным ребром. Иными словами, турниром называется орграф, полученный из полного графа Kn произвольной ориентацией его ребер.

• Теорема. В любом турнире существует ориентированный гамильтонов путь.

14. Планарные графы. Грань, степень грани, аналог теоремы Эйлера. Теорема (формула Эйлера), следствия. Теорема Куратовского (критерий Понтрягина-Куратовского). Примеры.

П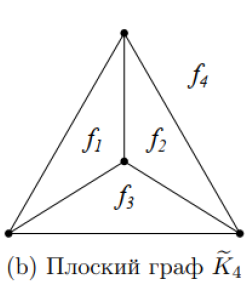 ланарным графом называется граф G, который можно нарисовать на плоскости так, чтобы изображающие его ребра отрезки кривых пересекались лишь в точках, изображающих вершины графа G. Такой способ изображения графа на плоскости называется правильным вложением графа в плоскость, а само изображение – плоским графом. Также употребляется термин укладка графа на плоскости.

Гранью плоского графа называется односвязная область, ограниченная ребрами графа. Одна из граней будет являться неограниченной, она называется внешней гранью, остальные, ограниченные со всех сторон – внутренними гранями.

Любая грань f плоского графа ограничена каким-то набором его вершин и ребер, образующих границу грани f. Говорят, что такие вершины и ребра инцидентны грани f. В свою очередь, две грани называют смежными друг другу, если границы этих граней содержат хотя бы одно общее ребро.

Степень грани f - это количество ребер, инцидентных данной грани.

Мосты – ребра, по обе стороны от которых лежит одна и та же грань.

Теорема Эйлера. Сумма степеней всех граней связного плоского графа равна удвоенному числу ребер.

Теорема (формула Эйлера). Количество вершин n, ребер m и граней r произвольного связного плоского графа удовлетворяют следующему соотношению: n - m + r = 2.

Доказательство. I) Вспомогательное утверждение: n - m + r = 2 верно для дерева: n, m = n – 1, r = 1.

II) По индукции: r = 1 верно. Предположим, что верно для всех плоских связаных графов с r-1 гранью. Покажем, что верно для любого связного графа с количеством граней r.

Т.к. r > 1, то существует хотя бы 1 простой цикл. Возьмем произвольное ребро е этого цикла, и пусть е – это граница граней f1 и f2. Удаляем e, грани сливаются, -1 грань. В новом графе получаем, что n1 – m1 + r1 = 2, n1=n, m1=m-1, r1=r-1 => n - m + r = 2.

• Следствие 1. Все правильные вложения одного и того же связного планарного графа G в плоскость имеют одинаковое количество граней.

• Следствие 2. Количество m ребер в произвольном простом связном графе, построенном на n≥3 вершинах, не превосходит 3n-6.

• Следствие 3. Любой простой связный плоский граф обязан иметь вершину, степень которой не превосходит 5.

• Следствие 4. Граф K5 не планарен.

Теорема (Куратовский, 1930). Граф G не является планарным тогда и только тогда, когда он содержит подграф, представляющий собой подразбиение K5 или K3,3.

15. Представление графов: матрица смежности, матрица инциденций, списки смежности. Преимущества и недостатки. Примеры.

Матрица смежности.

Матрица инциденций.

Список смежности.

16. Вершинная раскраска графа. Хроматическое число. Основные результаты. Теорема Брукса. Нижняя оценка. Теорема Мицельского.

Раскраска вершин – разбиение множества вершин на блоки-цвета

Вершинная раскраска графа G – это функция f:V→{1,2,3…,k} – множество цветов.

Раскраска вершин простого графа называется правильной, если любые две смежные вершины окрашены в разные цвета.

Любой граф, который допускает правильную раскраску своих вершин в k цветов, называется k-раскрашиваемым графом.

Наименьшее количество цветов, в которые можно правильно покрасить вершины графа G называется хроматическим числом λ(G) этого графа. Сам граф при этом называется k-хроматическим.

Теорема Брукса. (1941). Пусть G – простой связный граф, не являющийся полным графом или простым нечетным циклом. Тогда λ(G) ≤d, где d – максимальная из степеней вершин графа.